船闸船舶撞击力计算方法研究

鄢亚军

（上海市水利工程设计研究院，上海市 200333）

0 引言

船撞闸室结构属碰撞体系的力学问题。目前针对碰撞问题的研究主要采用的方法有理论方法、试验法以及有限元仿真分析方法等[1]。现阶段我国船闸设计中船舶撞击力是根据《船闸水工建筑物设计规范》（JTJ307—2001）上的撞击力公式计算所得，该公式是1967年苏联米哈依洛夫所著《船闸》一书中推荐的公式[2]，该计算公式中主要考虑了船舶吨位的影响，未考虑船舶撞击速度、撞击角度等因素的影响，从国内已有研究成果表明现有规范船舶撞击力结果偏小，计算公式有待进一步完善。本文以江苏某船闸闸室结构为例，考虑船舶橡胶护舷作用，应用ABAQUS软件中的Explicit显式动力分析模块对船舶、护舷、闸室结构、结构周边土体进行三维有限元数值模拟，模拟船舶动态撞击闸室过程，探讨船舶撞击力计算方法，为船闸水工建筑物设计提供参考。

1 船墙碰撞系统的运动方程

船舶与船闸闸室结构的碰撞问题属结构动力问题。本文通过ABAQUS软件中的Explicit模块建立船舶、护舷、闸室及结构周边土体三维数值模型，在总体坐标系中，船舶撞击闸室的动力方程可以表示为:

式中:[M]为质量矩阵；[C]为阻尼矩阵；[k]为刚度矩阵；{}为加速度向量；{}为速度向量；{u}为位移向量；{Fre}为包括碰撞力在内的外力向量。

利用ABAQUS中的速度预定义场赋予船舶初始速度，使船舶在初始惯性力作用下撞击闸室，系统获得初始动量，外力荷载F=0，进而可以根据动力方程求解结构力和应力随时间的动力响应。

2 有限元计算模型

2.1 工程概况

本研究采用江苏苏北运河上某重力式船闸闸室结构为例进行分析，该船闸建于20世纪80年代，闸室结构采用重力式钢筋混凝土结构，其断面见图1，闸室尺度230 m×20 m×5 m（长×宽×门槛水深）。根据实际通航情况，选取300 t、500 t、800 t、1 000 t过闸船舶作为研究对象，船舶相关尺寸见表1，闸室墙体、船舶的材料属性见表2；根据地质条件，土体建模范围处于砂壤土、软粘土层，土质材料参数见表3。

2.2 有限元计算模型

本研究采用ABAQUS/Explicit分析模块建立船舶、护舷、闸室结构及结构周边土体三维有限元模型。

（1）船舶简化模型

船舶简化为钢壳，采用壳单元模拟，壁厚取0.038 m，材料为弹塑性，船体排水量采用船体重量和货物总重量来模拟，货物采用实体单元，材料模型选择弹性材料模型，船舶底部采用法向约束，使船舶只能在水平方向上自由运动。

图1 闸室断面图（单位：cm）

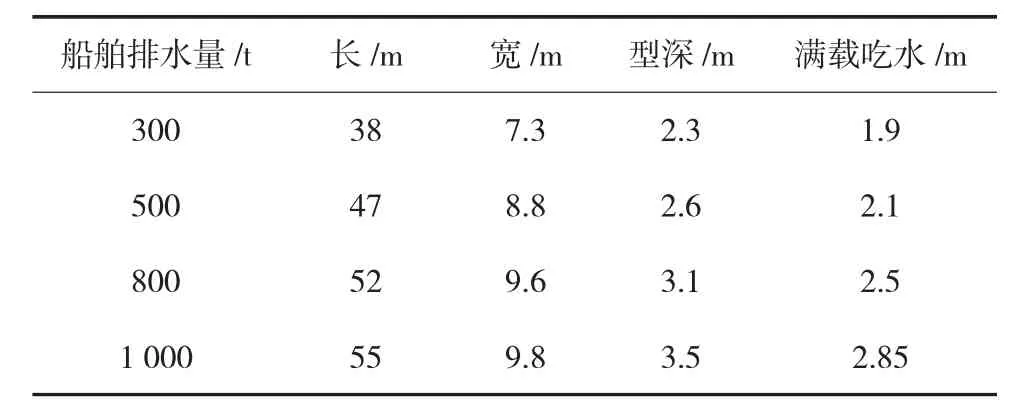
表1 船舶尺度

表2 闸室与船体材料

（2）橡胶护舷简化模型

考虑到船舶撞击过程中橡胶成分起主要缓冲作用，为简化橡胶护舷模型，忽略帘线复合材料及钢丝圈，建立内部挖空的环形结构模拟轮胎，采用单一的橡胶材料，取轮胎模型横截面宽度195 mm，高宽比70%，胎侧厚度15 mm，采用C3D8划分网

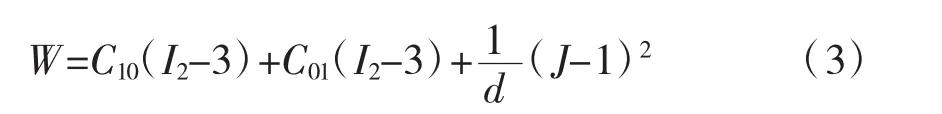
式中：W为应变能密度函数，是变形张量不变量I1、I2和 I3的函数；Cij、N 和 dp是力学性能常数。ABAQUS中采用的是二项三阶展开式，形式如式（3）所示：格单元，单元总数为8 316，胎侧面与船舷侧面采用绑定（Tie）约束，在船头可能的撞击处设置三个橡胶轮胎，橡胶材料采用双参数Mooney-Rivlin模型，其应变能密度函数[3]如下：

橡胶材料为不可压缩材料，取J=1。根据刘萌等研究确定Mooney-Rivlin模型中取0.807 3、C01取0.168 9，橡胶材料属性见表4，轮胎的有限元模型见图2。

表4 橡胶材料参数模型

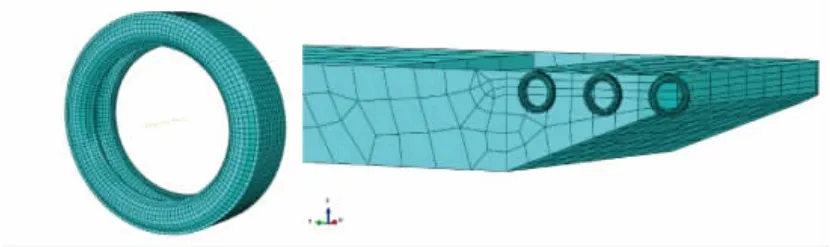
图2 轮胎护舷有限元模型

（3）闸室与地基土的计算模型

本论文模拟的船闸为分离式重力式船闸，沿船闸纵轴线取结构段对称的一半建立闸室模型。闸室结构纵向长20 m，横向底板宽12 m，高度11.7 m，采用实体单元建模，六面体网格划分，钢筋混凝土材料为线弹性，单元总数为8 480。根据地质条件，土体建模范围处于砂壤土、软粘土层。地基土建基面以下取13.5 m深，横向取对称面一侧50 m宽，建基面以上墻后回填土取与地基土体同宽。采用实体单元建模，土体材料为Mohr-Coulomb模型，单元总数为26 860，模型对称面施加正对称边界条件，其余三个侧面采用边界条件约束其法向位移，底部完全固定。

表3 土层参数

图3 船撞闸室有限元模型

3 数值模拟分析

根据水文资料可知，船闸上游最高通航水位+20.0 m，下游最低通航水位+14.5 m，考虑船舶低水运行，船舶撞击位置设在水位+17 m处。

船舶撞击闸室的最大角度按以下方法确定：设置船舶长度为Lα、宽度为Lb，则根据图4所示船舶与闸室宽度的关系可建立如下公式：

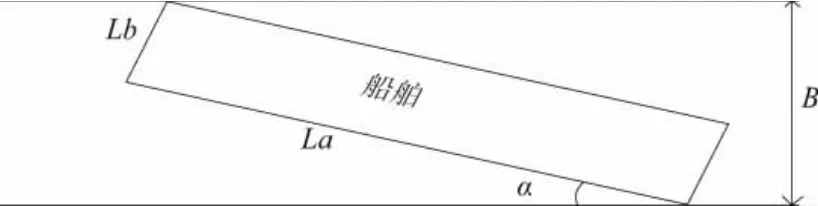
图4 船舶撞击角度示意图

根据式（5）可以得到各种船型在闸室中的理论最大撞击角度，见表5。由于实际过闸船舶不可能以最大撞击角度撞击闸室，故模型中船舶撞击角度取值均小于理论最大撞击角度。

表5 船舶理论最大撞击角度

3.1 平均撞击力与船舶排水量的关系

研究采用 300 t、500 t、800 t、1 000 t船舶安装橡胶护舷后以相同的撞击角度8°在0.5 m/s、0.8 m/s、1.0 m/s的速度下撞击闸室墙，通过软件模拟计算输出船舶撞击下的法向撞击力数值，得到九组撞击力时程曲线，对撞击力时程曲线积分可以获得撞击力时均值，该撞击力时均值即为平均撞击力。其撞击力平均值可按式（6）计算：

根据撞击力时程曲线得到平均撞击力计算结果见表6，利用模拟得到的撞击力数据可以画出图6所示的船舶撞击力与排水量的关系曲线。由图6可知，当船舶撞击角度和撞击速度一定时，平均撞击力数值随船舶排水量的增加而增大，但增大的趋势越来越缓。由于撞击力呈非线性增长的关系，根据图4可看出增长趋势符合幂函数增长规律，故可以采用幂函数的形式拟合。拟合形式为y=αXβ，拟合结果见表7，其相关系数≈0.988，表明拟合的曲线和数据是高度相关的。表中不同速度条件下的β值结果较为接近，平值值≈0.502，故可以近似认为其他条件相同时，船舶撞击力与船舶排水量的0.5次方成线性关系。

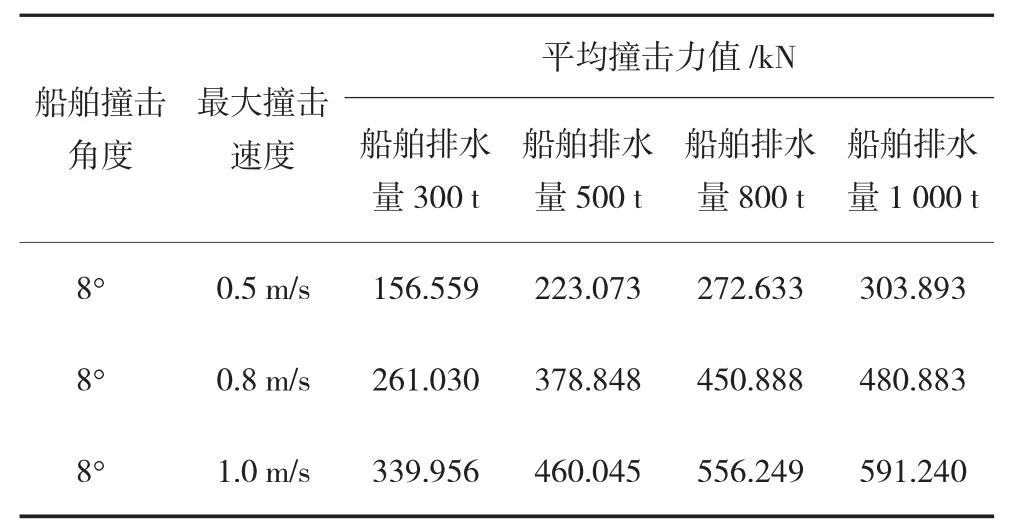
表6 不同吨位下船舶平均撞击力计算结果

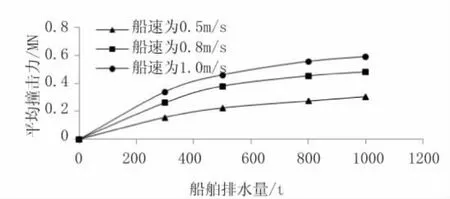
图6 船舶撞击力与船舶排水量的关系曲线

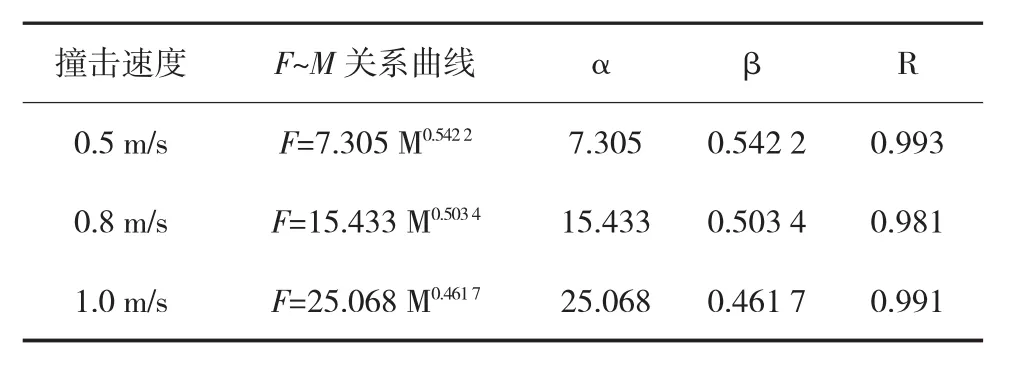
表7 平均撞击力F～船舶质量M关系曲线拟合

3.2 平均撞击力与船舶速度的关系

研究采用 300 t、500 t、1 000 t船舶安装橡胶护舷后分别以其在闸室的最大撞击角度撞击闸室墙体，输出船舶撞击的法向撞击力数值，得到撞击力时程曲线，可以计算出船舶的平均撞击力数值见表8，船舶撞击力与船舶速度的关系曲线见图7。从图7的曲线发展趋势可以看出当船舶排水量和撞击角度一定时，船舶法向平均撞击力随撞击速度的增加而增大，近似成线性关系。采用幂函数的形式进行拟合，拟合结果见表9，相关系数≈0.997，表明拟合的曲线与数据相关性较好。表中不同船舶排水量下的β值结果基本一致，平均值≈1.005，故可以近似认为其他条件相同时，船舶撞击力与船舶速度的1次方成线性关系。

表8 不同吨位下船舶平均撞击力计算结果

图7 船舶撞击力与船舶速度的关系曲线

表9 平均撞击力F～船舶速度V关系曲线拟合结果

3.3 平均撞击力与撞击角度的关系

研究采用300 t船舶安装橡胶护舷后,在8°、10°、15°三种不同角度下撞击闸室，输出船舶撞击得到的法向撞击力数值，计算得到船舶平均撞击力数值见表10，根据表10中的数据，可以得到如图8所示的船舶法向平均撞击力与撞击角度的关系曲线。由图8可以看出当船舶排水量和撞击速度一定时，船舶在较小的角度下撞击闸室墙，船舶的法向平均撞击力随撞击角度的增加而增加。采用幂函数的形式y=αXβ进行拟合，拟合结果见表11，相关系数≈0.9 983，拟合的曲线与数据相关性较好。表中不同船舶排水量下的β值结果基本一致，平均值≈1.1 157，近似认为其他条件相同时，船舶撞击力与船舶角度的1.1次方成线性关系。

表10 不同角度下的船舶平均撞击力计算结果

图8 船舶撞击力与船舶撞击角度的关系曲线

表11 平均撞击力F～船舶撞击角度θ关系曲线拟合结果

3.4 使用橡胶护舷前后的平均撞击力对比

研究采用 300 t、500 t、1 000 t船舶分别在有橡胶护舷和无橡胶护舷的条件下以相同的撞击角度 8°在 0.3 m/s、0.5 m/s、0.8 m/s的速度下撞击闸室墙得到的法向平均撞击力值见表12，通过九组数据的比较可知不同吨位的船舶在安装橡胶护舷后法向平均撞击力均有大幅减小，其撞击力与未安装橡胶护舷的撞击力数值比值均大于1.70:1，说明过闸船舶安装橡胶护舷后能大幅减小撞击力，减轻船舶对结构物的损坏。

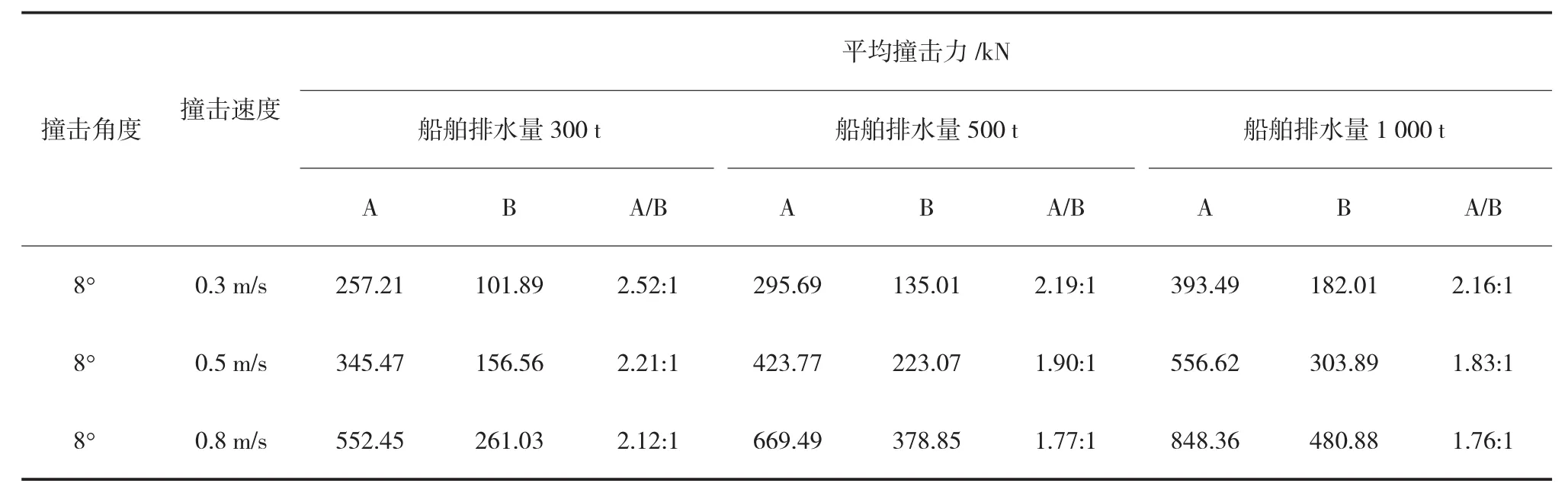
表12 不同吨位下的船舶使用护舷前后的平均撞击力对比结果

4 结论

（1）本文采用ABAQUS软件中的Explicit显式动力分析模块模拟了不同工况下考虑橡胶护舷的船舶动态撞击闸室墙过程。由软件计算结果可知，当其他条件相同时，过闸船舶撞击闸室的平均撞击力近似与船舶排水量的0.5次方近似成线性关系；与撞击速度的1次方成近似线性关系；与撞击角度的1.1次方近似成线性关系。

（2）设置橡胶护舷前后的船舶法向平均撞击力数值对比结果表明，过闸船舶安装橡胶护舷后法向平均撞击力显著减小，减轻了船舶对结构物的损坏。