倒挂井壁法竖井衬砌结构受力分析
张增峰
(上海市城市建设设计研究总院(集团)有限公司,上海市 200125)
0 引言
地铁暗挖车站一般埋置较深,且地面建筑物多,交通繁忙,施工时为运输隧道内材料并增加土石的出入口需设置施工临时竖井。
竖井结构设计计算时通常是将其简化为平面问题处理,采用半经验的方法。但是竖井结构为保证足够刚度,往往在内部设置圈梁、腰梁等加强结构,同时竖井壁承受的侧向荷载随深度的增加也在不断变化,这与平面问题的假设条件不符。因此在设计中应考虑竖井结构的空间效应。
井壁侧土压力的分布主要可归纳为两种:(1)线性增加型——不考虑井筒掘进半径的影响,随深度呈曲线增加。(2)极限型——地压力与井筒半径有关,深度达到一定值时,地压力趋于一极限值。徐伟等[1]通过三维离型机模型试验,得到深厚覆盖层下竖井井壁外侧的应变数据,其变化趋势为竖井井壁环向应变整体上先增后减,在距地表0.5H(H为竖井深度)处,竖井应变达到最大值。崔广心[2]通过研究指出,深层地压的复杂性大于目前的认知,对于达到某一深度后水平地压趋于定值的结论并未得到足够的工程实测资料证实,人为减小地压值很可能给工程造成隐患。胡金平等[3]通过有限元模拟认为,由于井筒周围围岩开挖卸载,应力迅速减少,可能因井底成为临空面而导致井筒侧壁出现拉力。朱正国等[4]研究认为:竖井围护结构是一种四边相互支撑的闭合结构,具有显著的空间受力特性,经典土压力理论与假设工程实际相差较大,导致围护结构设计偏于保守。
围岩压力计算是竖井结构设计的基础,若侧压力值取值太大将使结构设计过于保守,造成不必要的浪费,若取值太小则结构设计偏于不安全。目前设计院一般采用半经验方法,将其简化为平面应变模型,取最大侧压力处的衬砌内力进行包络设计。该方法虽未发生较大的问题,但井壁在不同深度、不同土层采用相同的格栅间距不符合客观实际且设计概念不清晰。
本文以贵阳市轨道交通3号线北京路站1号竖井结构设计为背景,建立三维有限元数值模型,分析不同侧向土压力模型下结构的受力情况并与传统平面应变模型计算结果比较,得出相应结论,为以后类似工程提供优化设计借鉴。
1 工程背景
贵阳市轨道交通3号线北京路站位于安云路与北京路十字交叉路口下方,与轨道交通1号线换乘,1号线车站沿安云路呈南北方向布置,3号线车站沿北京路呈东西方向布置。从经济角度考虑,1号竖井与车站风井结合设置,位于车站西南角(见图 1)。
1.1 车站竖井地质情况
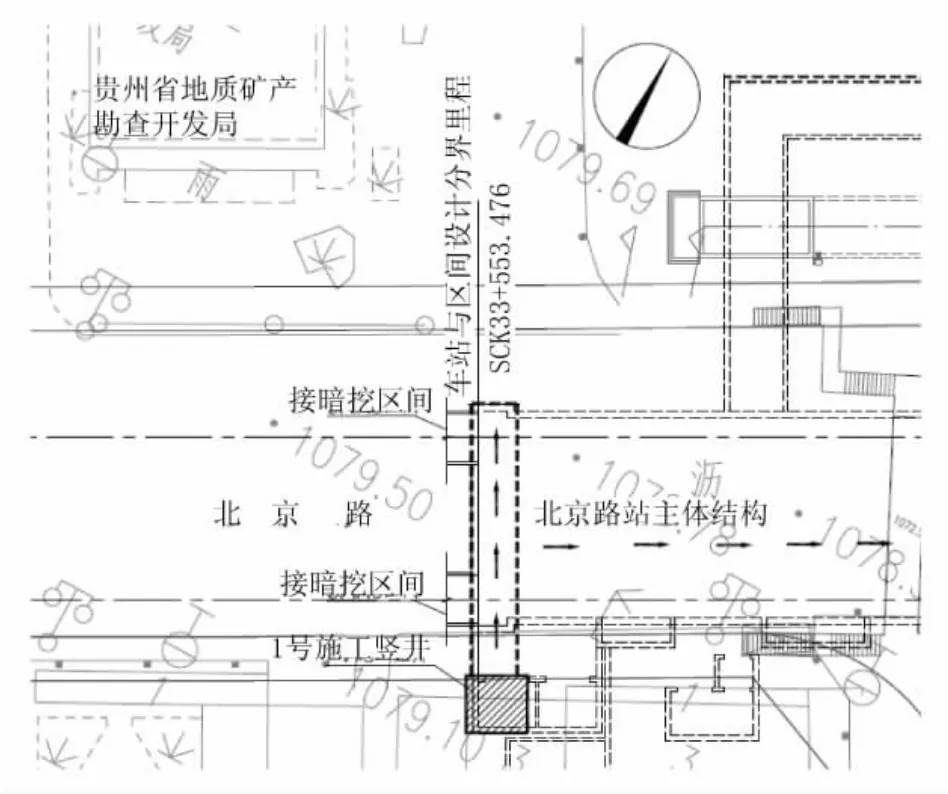
图1 1号竖井总平面图
本站竖井开挖深度范围内主要涉及<1-3>块石层、<4-1-1>硬塑红黏土、<4-1-2>可塑红黏土、<14-2-3>中风化白云岩。红黏土呈黄褐色、棕黄色,软塑状,土质纯,具有高液限、遇水软化、失水强烈收缩、裂隙发育、易剥落的工程性质,局部具弱膨胀性;中风化白云岩呈灰色、浅灰色厚层至块状细-中晶白云岩或紫红、肉红、灰黄薄至中厚层泥晶灰白云岩夹膏盐岩,时夹溶塌角砾岩,岩芯敲击声较脆,节理较发育。车站竖井地层参数见表1。表1中:hi为各土层厚度,m;γ为土体天然重度,kN/m3;ν为泊松比;Eref为地层弹性模量,MPa;cref为土体粘聚力,kN/m2;φy为土体内摩擦角,(°)。
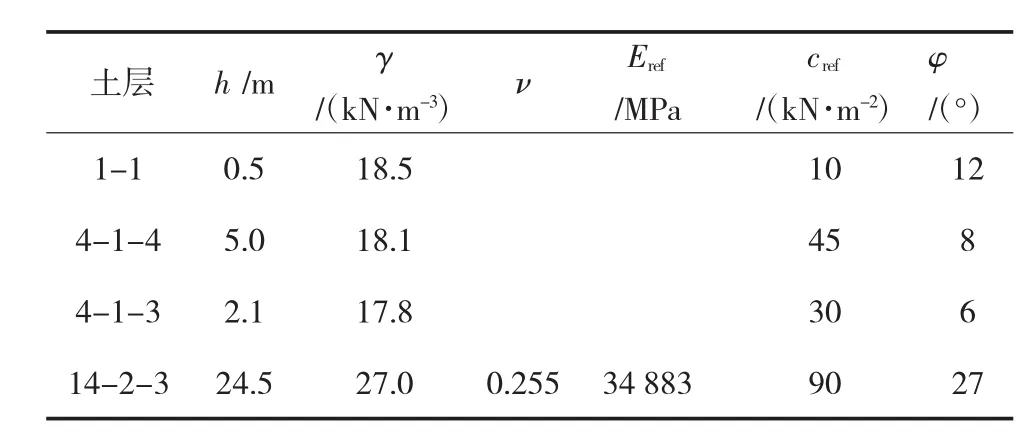
表1 地层参数表
1.2 支护结构参数
竖井采用倒挂井壁法施工,井壁初期支护采用C25喷射混凝土,厚度350 mm,格栅钢架采用4根25主筋,每榀格栅钢架中心间距0.5 m,侧壁采用22砂浆锚杆,长3.5 m,梅花形布置,水平间距1.0 m,水平夹角30°。井口设置1.0 m×1.5 m锁口圈梁,开横通道马头门上方设置0.6 m×0.8 m腰梁。竖井设计深度为32.1 m,竖井底部采用8@200 mm×200 mm钢筋网(双层)封底。1号竖井平、剖面如图2所示。
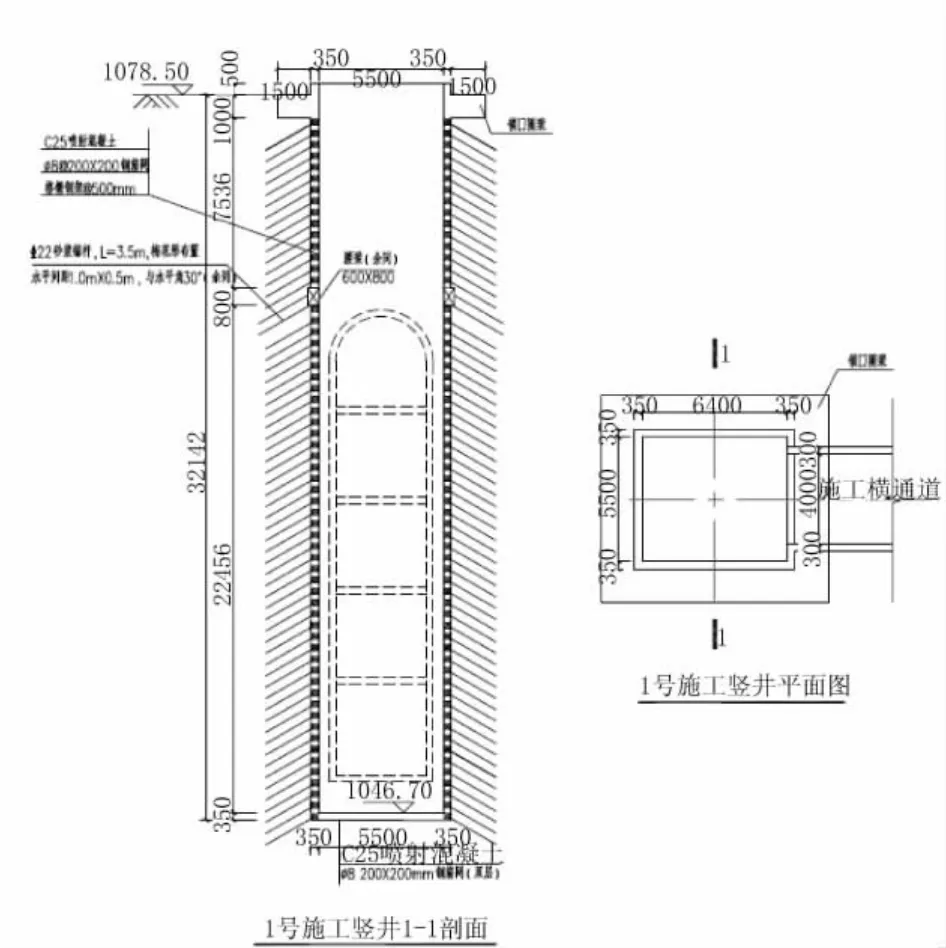
图2 竖井支护结构平、剖面图(单位:mm)
2 竖井侧向压力
2.1 侧向压力模型的选择
(1)朗肯土压力公式因概念清晰、计算简单而被广泛应用于土压力计算中。根据朗肯土压力计算公式可得:
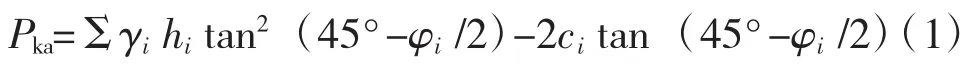
式中:Pka为主动土压力系数;γi、hi分别为第 i层地层重度(kN/m3)和厚度(m);φi为第 2 层土体内摩擦角,(°);ci为第 2 层土体的黏聚力,kPa。
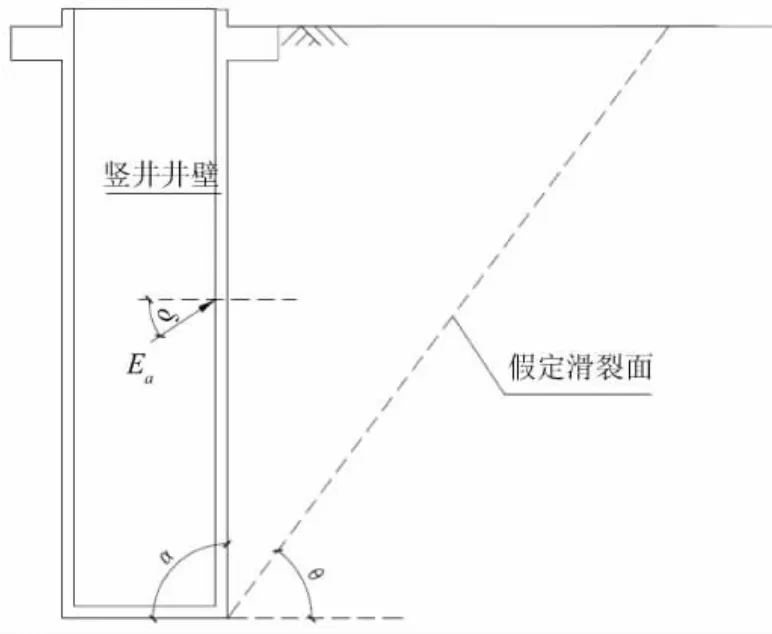
图3 竖井井壁土压力计算
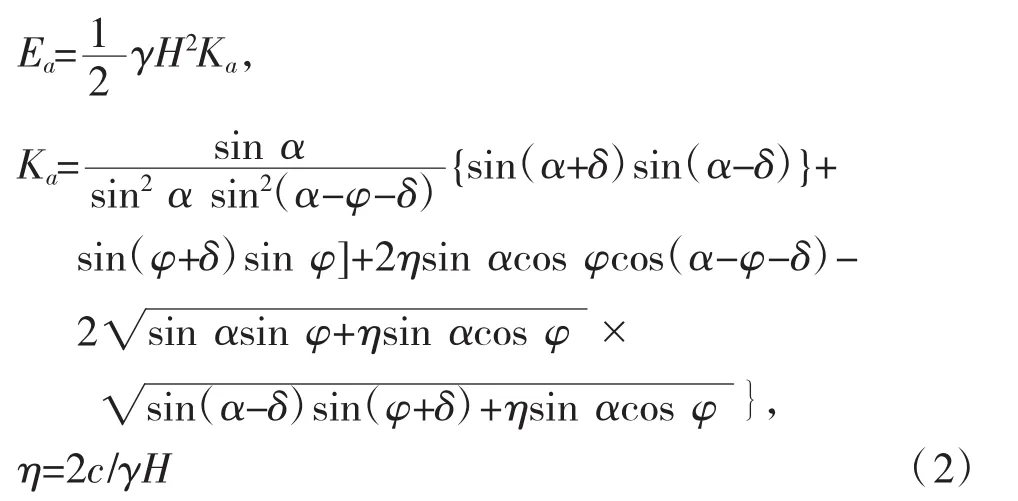
(2)侧向岩土压力也可采用库伦土压力公式求解。根据平面滑裂面假定(见图3),主动土压力合力可按照下列公式计算:式中:Ea为相应于荷载标准组合的主动土压力合力,kN/m;H为竖井深度,m;δ为土对挡土墙墙背的内摩擦角,α为支挡结构墙背与水平面的夹角;其余符号含义同公式(1)。
挡墙侧压力分布可根据锚杆层数、挡墙位移大小、支护结构刚度和施工方法等因素,简化为三角形、梯形或当地经验图形。北京路站竖井主要位于中风化灰岩中,侧压力可近似按照图4确定。
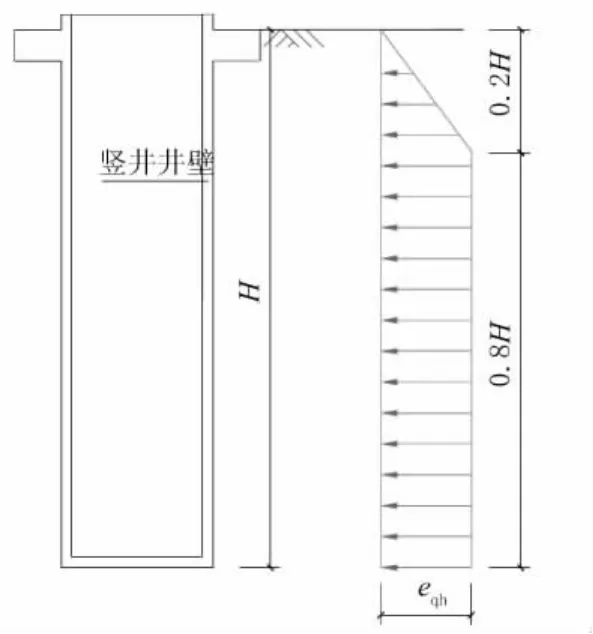
图4 竖井井壁侧压力分布图
图中 竖井井壁的侧压力:

式中:eah为相应于作用的标准组合时侧向岩土压力水平分力,kN/m2。
(3)《公路隧道设计细则》(JTL/T D70—2010)中指出,对于公路隧道通风竖井围岩压力可按秦氏方法进行计算,假定竖井周围每层岩石受到破坏时出现滑动棱柱体,将其上的覆盖层视为作用于破坏棱柱体上的均布荷载,则竖井的围岩压力为:
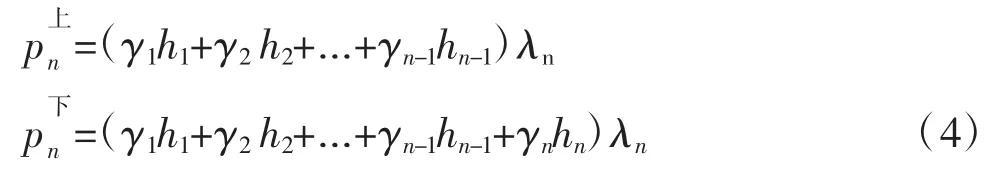
2.2 侧向压力计算
(1)根据朗肯土压力计算公式(1),竖井侧向压力随深度的变化值见表2。表2中,当计算值Pka<0 时,取 Pka=0。
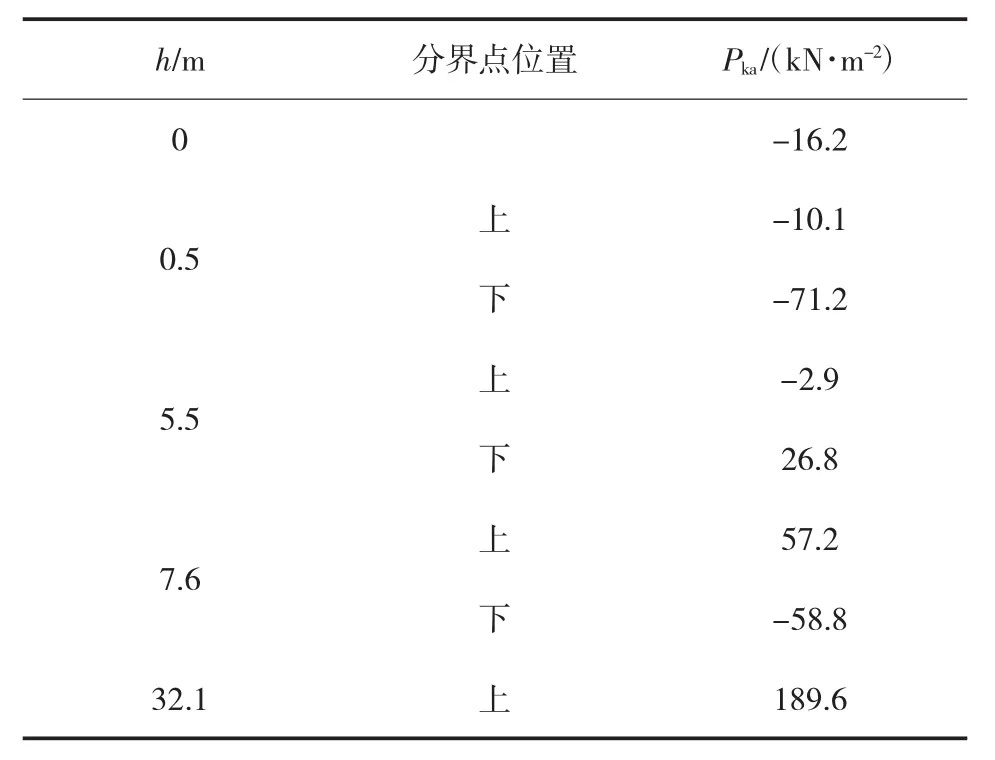
表2 围岩侧向压力变化表(朗肯土压力)
(2)采用库伦土压力公式(2),竖井侧壁承受的主动土压力Ea计算如下:
取 c=90 kPa,γ=27 kN/m3,H=32.1 m,φ=27°,因墙背粗糙,可取δ=0.5φ=13.5°,将以上参数代入公式(2)可得:
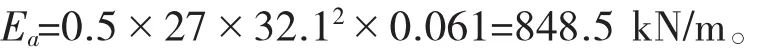
由公式(3)可得:
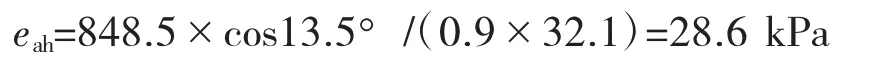
(3)采用秦氏算法进行计算,竖井侧向压力随深度的变化值见表3,根据《公路隧道设计细则》中表20.2.7-1,其中的λn取相应土层的平均值。
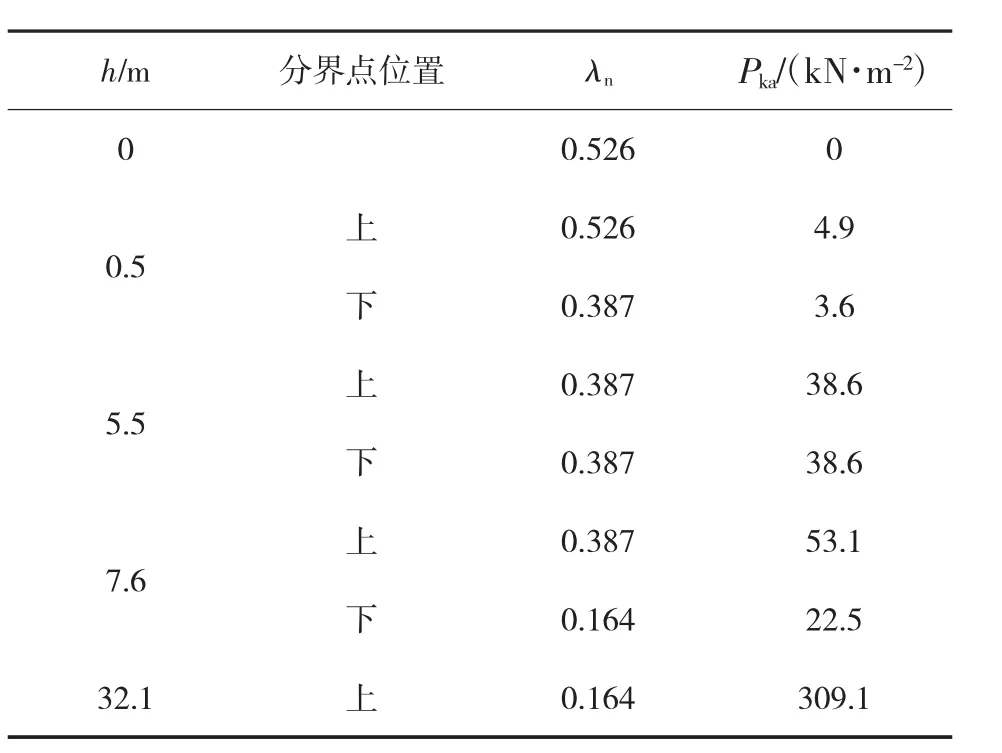
表3 围岩侧向压力变化表(秦氏算法)
3 有限元计算
3.1 模型建立
3.1.1 平面应变模型
平面应变模型基于结构分析软件ANSYS,采用荷载-结构模型平面杆系有限元法进行竖井衬砌结构的计算与分析。衬砌结构选取梁单元(beam3),围岩弹性抗力采用弹性杆(link10),竖井的侧向弹簧刚度取所在土层水平基床系数。荷载结构计算简图见图5。
3.1.2 三维梁-壳单元模型
三维梁-壳单元模型同样基于结构分析软件ANSYS,采用荷载-结构模型三维梁-壳有限元法进行竖井衬砌结构的计算与分析。衬砌结构选取壳单元(shell63),锁口圈梁采用梁单元(beam188)。荷载结构计算模型见图6。
图5 竖井衬砌计算简图

图6 竖井衬砌三维梁-壳单元模型
3.2 计算结果及安全分析
取各侧向土压力计算模型计算所得的侧向压力最大值加载于平面应变模型中,分别得出结构的弯矩、轴力及最不利截面出现的位置。
将各测向土压力计算模型计算所得的侧向压力随深度变化值加载于三维梁-壳单元模型中,得出竖井井壁的弯矩、轴力以及最不利截面出现的位置。
平面应变模型计算结果见图7~9,平面应变模型最不利截面处内力及配筋量见表4。
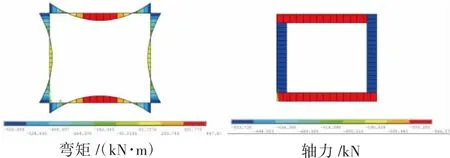
图7 朗肯土压力计算衬砌内力
三维梁-壳单元模型计算结果见图10~12,三维梁-壳最不利截面处内力及配筋量见表5。
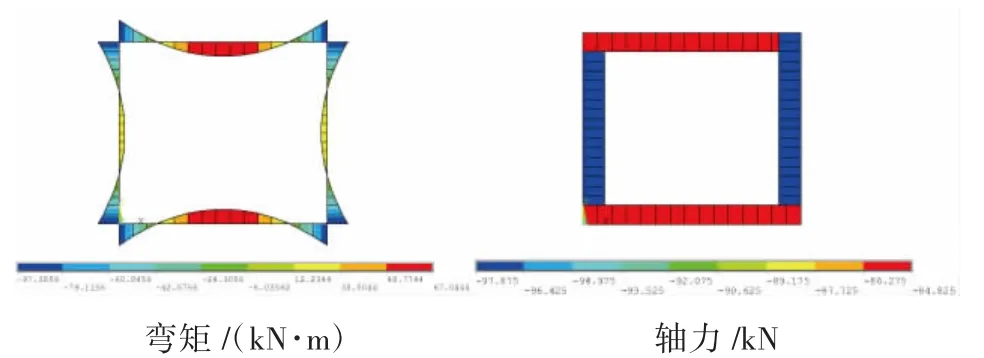
图8 库伦土压力计算衬砌内力
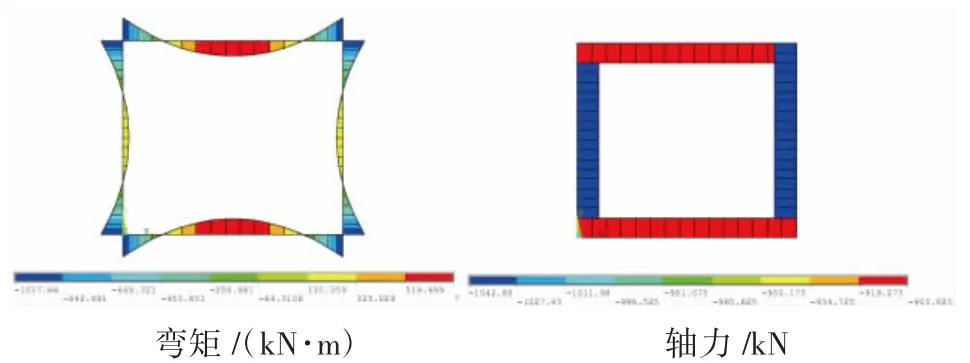
图9 秦氏土压力计算衬砌内力

表4 平面应变模型最不利截面处内力及配筋量

图10 朗肯土压力计算井壁内力(单位:kN·m)
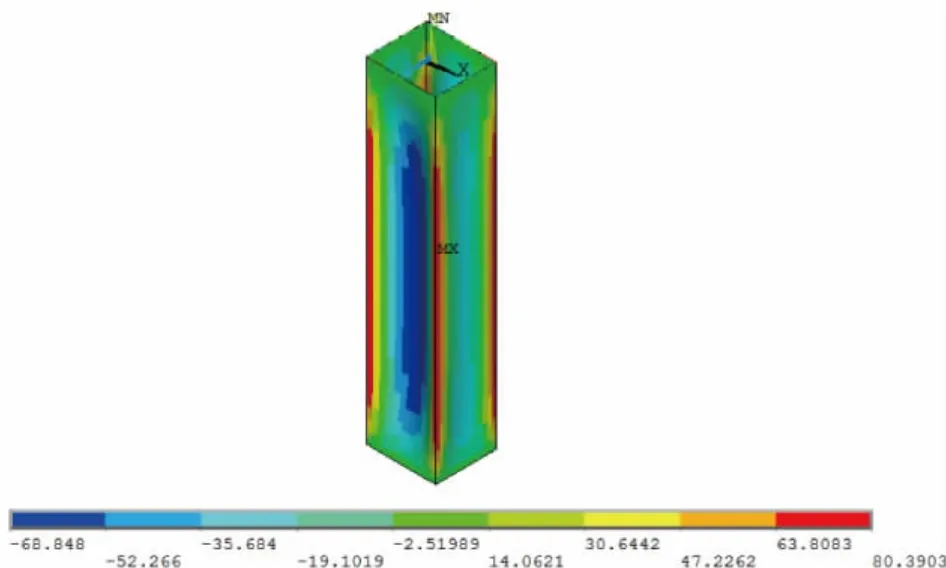
图11 库伦土压力计算井壁内力(单位:kN·m)
对平面应变模型与三维梁-壳单元模型计算结果进行对比可知,平面应变模型所得的弯矩及轴力均大于三维梁-壳单元模型的计算结果,且无法了解最不利断面所处深度;后者考虑到竖井结构的空间效应,更符合竖井衬砌的实际受力工况。

图12 秦氏土压力计算井壁内力(单位:kN·m)
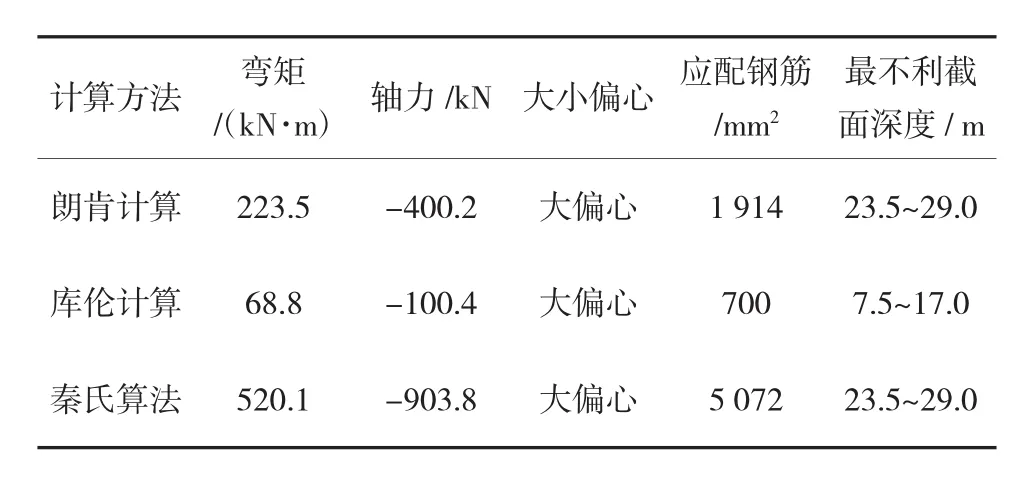
表5 三维梁-壳单元模型最不利截面处内力及配筋量
三维梁-壳单元模型计算所得井口至马头门上方(深度约6~7 m)竖井井壁的内力较小。竖井衬砌最不利断面往往处于井底以上5~8 m范围内。
根据计算结果,采用朗肯土压力公式、秦氏算法计算所得井壁的弯矩及轴力均远远大于库伦土压力计算结果。若采用秦氏算法计算所得的结果进行衬砌配筋,则初支结构衬砌配筋量过大。
对本地区相似车站及区间竖井支护后的工程进行类比,实际衬砌每延米配筋为425(实配受拉钢筋面积As=1 964 mm2/m),配筋量均远小于以上秦氏算法计算所得的理论值。每榀格栅钢架配筋见图13。
根据类似工程的监测数据,采用朗肯土压力计算结果进行设计的衬砌结构,在使用期间井壁的水平变形已收敛,井壁周边无明显裂缝,基本处于稳定状态。
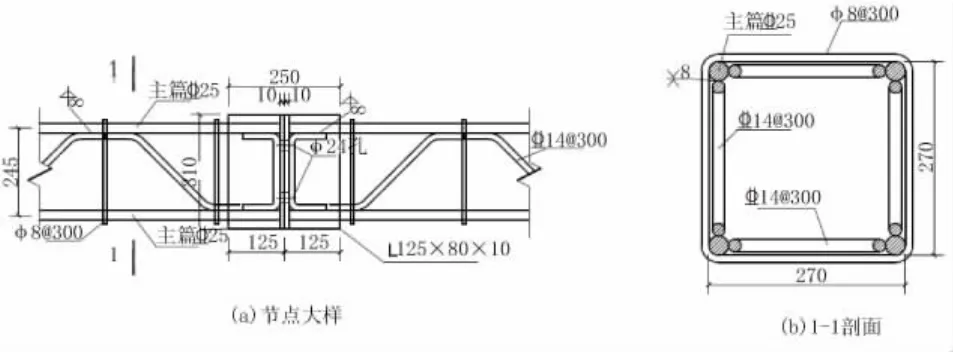
图13 格栅钢架配筋详图(单位:mm)
4 结论
(1)采用秦氏算法计算的围岩侧向压力在同一岩层中线性增加,井底处围岩压力较大。根据开挖应力分析表明,因井壁周围围岩开挖卸载而使应力迅速减小,用秦氏算法计算所得竖井侧向压力过于保守,造成设计过程中配筋困难。
(2)朗肯主动土压力的计算假定为:墙背直立光滑、土体表面水平,而竖井衬砌结构为喷射混凝土,且每榀格栅周边均匀打设砂浆锚杆,墙背粗糙且与周边地层结合较好,故若围岩侧向压力直接采用朗肯土压力计算可能与实际工况存在偏差,但按此方法计算可基本满足安全施工的要求。
(3)库伦土压力假设破裂面不确定,若竖井开挖深度内岩(土)层分布复杂,则破裂面无法确定,从而导致墙背主动土压力计算结果偏差较大,在复杂地层中难以把握井壁的实际承受侧向压力,按库伦土压力设计衬砌结构可能给工程造成隐患。
(4)竖井设计忽略了锁口圈梁、腰梁、封底格栅的刚度,未考虑其对竖井的约束作用,且竖井在马头门上方的衬砌内力较小,宜适当增大格栅间距。
(5)竖井的围岩应力场研究不够透彻,导致竖井衬砌结构设计过于保守。建议竖井围岩设计时根据更多工程经验,修订或改进传统朗肯土压力理论,便于设计人员在工程中应用。

