混合储能多目标容量优化配置

李世泽，高素萍，郭朝江

（1.哈尔滨工业大学深圳研究生院，深圳518055；2.深圳职业技术学院机电工程学院，深圳 518055）

随着能源日趋紧张及低碳能源的发展需求，全球都在努力发展新型能源应用模式，储能技术作为新能源应用的关键环节[1]，其储能元件的选择与运行的控制策略等都需要研究解决。近来，分布式发电中常用的储能设备是锂离子电池或铅酸电池[2-3]，但有关研究发现，将蓄电池与超级电容混合配置作为储能设备可以有效减少蓄电池充放电次数，延长电池的使用寿命[4]。

储能的容量配置是分布式发电系统或微网系统规划设计阶段的一项重要内容，如何根据负荷需求及发电量来最大程度地保持系统的供需平衡，决定了系统的经济性和可靠性[5]。文献[6]分析了含多种分布式电源的微网的混合储能优化配置方案，但该配置仅以总成本为目标函数；文献[7]应用加强帕累托算法求解风光柴储系统多目标优化配置问题，但是其配置对象为光伏板、风机组、柴油发电机和蓄电池，储能装置未涉及超级电容，且未考虑能量过剩指标；文献[8]使用改进两阶段模型求解算法来寻找多个场景的最优解，并表明控制策略对设计规划阶段的混合容量配置有一定影响，通过在设计阶段就考虑全生命周期内控制策略的准稳态仿真来减小储能成本，但没有考虑系统的电能质量问题。在容量优化配置模型上，国内学者大多应用预测到的全年光照、风速等数据，利用HOMER软件，仿真设计不同类型能源组合时的系统性能指标[9-10]，该方案可以结合控制策略模拟微网整个周期的运行情况，但是由于HOMER软件的局限性，只能在限定条件下得出经济成本最优的配置结果。文献[11]研究了高校、工业区、居民区、商业区和农业区5类典型微电网的新型负荷特性，分别从用户收益角度和供电可靠角度设计容量配置模型，但此两个角度均为单一目标函数，且没有考虑负荷缺电指标。

综上所述，大部分学者对储能装置容量配置集中在单一装置上，对混合储能装置容量配置目标认识不全面，这样会限制储能系统其他特性。混合储能系统涉及能量型和功率型储能设备，进行容量配置前需要结合控制策略来解决对不平衡功率分配的帕累托最优问题。为了使优化配置结果更接近实际需求，提出一种考虑全生命周期成本、供电可靠性指标和缺电率指标、供需平衡的多目标储能容量优化配置模型，并在全生命周期内仿真检验各项指标。

1 分布式混合储能系统

1.1 分布式发电系统

分布式发电系统采用主动式混合储能结构，系统中的超级电容和铅酸蓄电池都通过各自的变流器接入直流总线，如图1所示。主动式混合储能相比于被动式结构，可以灵活控制超级电容和铅酸电池的充放电功率。光伏系统和风电系统，通过各自最大功率变换器接入直流总线。

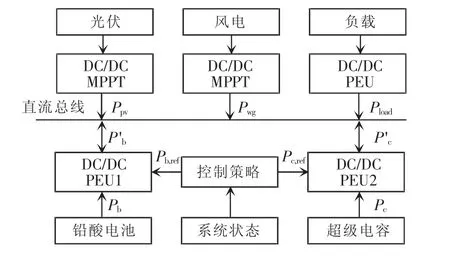
图1 孤立分布式发电系统Fig.1 Isolated distributed generation system

在主动式混合储能的独立分布式发电系统中，由于脱离大电网支撑，因此新能源发出的能量需要在系统内部消纳，即供需动态平衡，表示为

式中：PRE为光伏和风电系统发电功率；PHESS为超级电容和蓄电池总功率；PLOAD为负载功率；考虑储能变换器的效率，P′b为超级电容通过电力电子变换器后的功率；P′c为蓄电池通过变换器后的功率；忽略发电最大功率变换器功率损耗，Ppv为光伏发电功率；Pwg为风电发电功率。

1.2 混合储能控制策略

基于滤波器的控制策略使用一个滤波器将剧烈波动的混合储能动态需求功率分解为高频部分和低频部分[12]，分别表示为Plow和Phigh。这个方法简单而且计算量小，很适合用于实时控制。

已知负荷功率曲线、光伏发电曲线和风力发电曲线，针对蓄电池和超级电容混合储能系统的容量优化配置问题，将3个典型曲线都分为N份，组成负荷瞬时功率、光伏瞬时功率和风力发电功率3个数组：{PL（1），PL（2），…，PL（N）}、{PPV（1），PPV（2），…，PPV（N）}、{PWG（1），PWG（2），…，PWG（N）}。

假设控制策略使用低通滤波器，将需求功率的高频部分分配给超级电容，将低频部分分配给蓄电池，则有

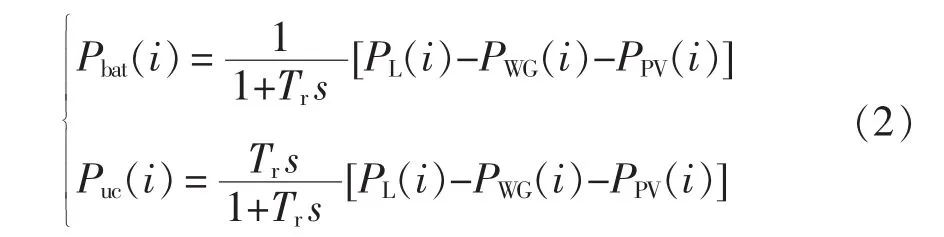
式中：Pbat（i）和 Puc（i）分别为蓄电池和超级电容第 i时刻给定瞬时输出功率；Tr为低通滤波器时间常数；PL（i）为负荷第 i时刻瞬时消耗功率；PPV（i）为第 i时刻光伏瞬时发电功率；PWG（i）为第i时刻其他新能源瞬时发电功率。

1.3 混合储能容量配置

由文献[13]可知混合储能配置的超级电容和蓄电池的容量和功率，在微电网的整个运行周期中，储能均未出现单一储能系统中遇到的SOC和功率限幅问题。与此同时，混合储能配置的最优容量要小于单一储能的优化容量，充分发挥了超级电容的快速处理功率的能力。相比较于蓄电池储能系统的容量配置问题，混合储能系统的容量配置需要同时考虑两种设备的配置功率和配置容量。蓄电池和超级电容瞬时功率分配情况由控制策略及式（2）中低通滤波时间常数Tr决定，而针对每个Tr，都可以找到蓄电池和超级电容的1对最优解，变成一个帕累托最优问题，最后通过枚举法找到总目标函数最优值。

2 容量优化配置模型

2.1 配置模型

在微网或分布式发电规划设计阶段，使用单目标容量优化模型往往会为了降低成本而牺牲系统的可靠性等其他性能指标，而使用多目标容量优化模型，能够得到更合理的配置容量[6]，因此本文使用多目标容量优化配置模型。在多目标规划问题中，通过将多个子目标的适应度线性加权组成单一适应度函数，考虑一些约束条件组成多目标优化模型，即

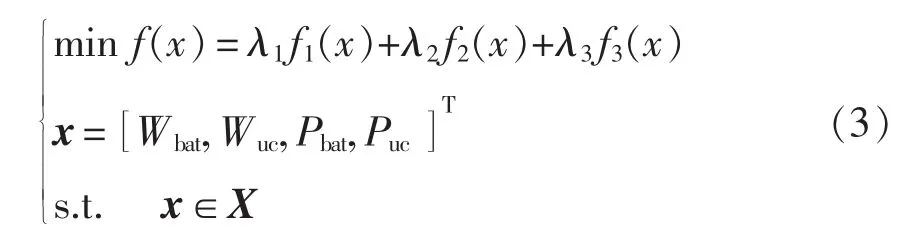
式中：f（x）为聚合后的最终目标函数；f1（x）为成本子目标函数；f2（x）为供电可靠性及能量过剩子目标；f3（x）为供求平衡子目标；x为配置变量，包括蓄电池能量、超级电容能量、蓄电池功率和超级电容功率；Wbat为蓄电池能量；Wuc为超级电容能量；Pbat为蓄电池功率；Puc为超级电容功率；X为变量x的约束条件，包括蓄电池荷电状态SOC约束条件、超级电容端电压VOC约束条件和最大功率约束条件；λ1、λ2、λ3分别为子目标函数的权重。

2.2 子目标函数

1）成本子目标函数

混合储能成本包括初始建设成本和后期维护费用，综合考虑蓄电池和超级电容能量和功率，有

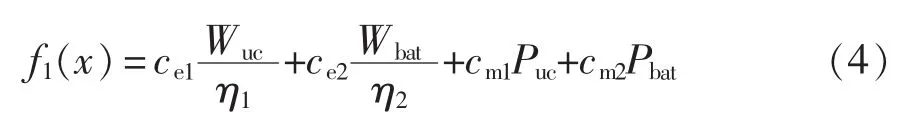
式中：η1和η2分别为混合储能系统中超级电容和蓄电池的效率；ce1和ce2分别为混合储能系统中超级电容和蓄电池单位容量价格；cm1和cm2分别为混合储能系统中超级电容和蓄电池单位功率的维护成本。

2）供电可靠性和能量过剩子目标函数

微电网中的电能不进行并网，因此如果发电功率大于负荷功率加储能吸收功率，会造成功率浪费；如果发电功率加储能放电功率小于负荷功率，又会造成系统不可靠。因此通过蓄电池的配置功率和实际分配的功率差的平方和来表示供电可靠性和能量过剩子目标，即

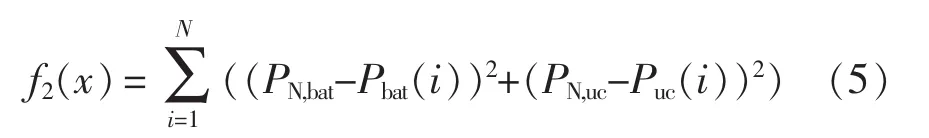
式中：PN,bat为蓄电池配置的额定功率；PN,uc为超级电容配置的额定功率。

3）供需平衡子目标函数

混合储能系统需要保证蓄电池和超级电容提供或吸收的功率变化尽量小，来保证系统的稳定性，因此以蓄电池和超级电容提供功率方差为目标，建立供需平衡目标函数，即

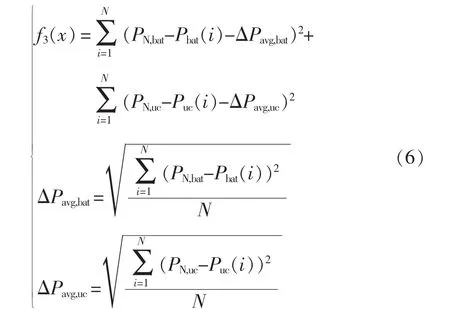
式中：ΔPavg,bat和ΔPavg,uc分别为蓄电池和超级电容的平均功率偏差。

2.3 子目标函数权重

混合储能容量配置中含有多个子目标函数，根据实际情况权衡各个子目标函数的重要性，使用自适应度排序法来确定各个子目标函数的权重。不同容量配置与最优配置的差叫离差，表示为

自适应度排序法来确定各个子目标函数的权重步骤如下。

步骤1假设有m个子目标函数，按照单一目标最优情况各自求解m个子目标函数fi（x）的最优值xi。

步骤2将单一目标求得的最优解集代入所有的子目标中，得到最优解集对应的最优配置

步骤3针对不同目标函数的最优解xj，求解此值对其他各目标值的差值，如式（7）所示。某一子函数最优解在其他函数中的函数值为次优解，与最优解的差值均非负。

步骤4计算各子目标函数的离差度，则

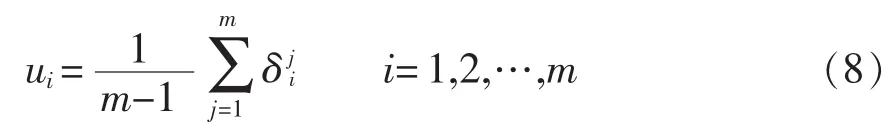
步骤5计算子目标函数权重，则

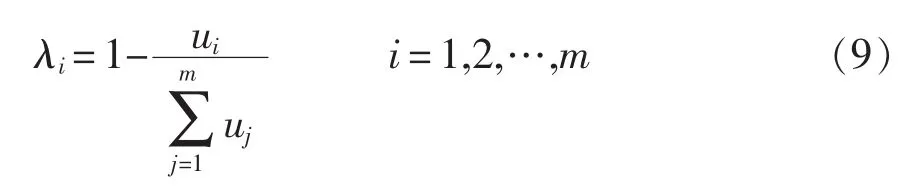
步骤6由于离差均为非负，通过上述过程计算出的权重均为正值，再将权重归一化，即

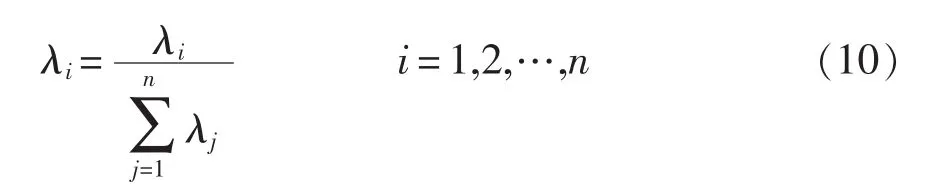
式中：n为子目标函数个数；λi为个子目标函数的权系数，。

2.3.1 约束条件

1）蓄电池荷电状态SOC约束条件

为了防止损坏蓄电池和超级电容的寿命，限制蓄电池SOC的上下限，即

式中：SOCmin为蓄电池荷电状态下限，一般取20%～30%；SOCmax为蓄电池荷电状态上限，一般取80%～100%。

2）超级电容端电压VOC约束条件

为了防止降低超级电容的寿命，限制超级电容端电压VOC上下限，即

其中，VOC,min一般取 10%～20%，VOC,max一般取 90%～100%。

3）最大功率需求约束条件

系统中可能有一些重要负荷，需要保证这部分负荷不能断电。因此有一个最小功率需求，同时保证最大功率不超过各变换器最大功率限制，即

式中：Pmin为最小功率需求；Pbat,max和Puc,max分别为蓄电池和超级电容最大功率限制。

2.4 容量优化算法

运用多目标粒子群算法时，本文采用两阶段优化迭代求解策略。第1阶段计算种群各个体对3个目标函数的适应度，求对应解对其他各适应度的差值，通过离差排序法得到各粒子的权重值λi；第2阶段各粒子通过跟踪聚合后目标函数的2个 “极值”来更新自己，第一个极值是粒子本身所找到的局部最优解pBest；另一个极值是整个种群目前找到的全局最优解gBest。重复上述两个阶段，直至满足终止条件。本文将更新代数作为多目标粒子群算法的终止判据，最后一代种群的所有非支配解构成的集合即为所研究问题的最优解集。

针对粒子群优化容易产生早熟收敛、全局寻优能力较差等特点，本文对其做如下改进[14]：在第1阶段开始时，以较小概率为各粒子的位置和速度增加随迭代次数递减的阻尼扰动，以此来加强全局寻优能力，避免粒子群算法早熟，同时还可提高搜索精度。

使用改进多目标粒子群算法对上述目标函数进行求解。混合储能容量优化配置求解流程如图3所示。

步骤1首先进行容量优化配置的初始化。读取风机、光伏、混合储能设备和粒子群算法参数，并随机生成铅酸蓄电池和超级电容的N组容量配置解集 xi=[Wbat,i,Wuc,i,Pbat,i,Puc,i]T。

步骤2评价N组容量配置。分析N组混合储能的配置情况，在使用低通滤波器的控制策略下对典型风光数据和负荷数据进行补偿。若实时控制中，不能满足所描述的约束，则该配置无效，需重新配置再进行评价；若能满足约束条件，则计算N组容量配置的各目标函数值。

步骤3随机增加各粒子位置和速度阻尼扰动。为了克服粒子群算法易陷入局部最优的问题，按照迭代次数以一定概率增加阻尼扰动。

步骤4利用离差排序法计算权重，并聚合目标函数，计算适应度。

步骤5判断合理性并进入第2阶段。更新N组各自历史最优配置和总的最优配置。在N组配置都完成评价后，使用这N组配置，与各自历史值进行比较得到个体最优值；然后使用个体最优值和历史最优值进行比较，最终得到个体最优解和总体最优解。

步骤6按照粒子群算法中的位置公式和速度公式更新下一组容量配置，即

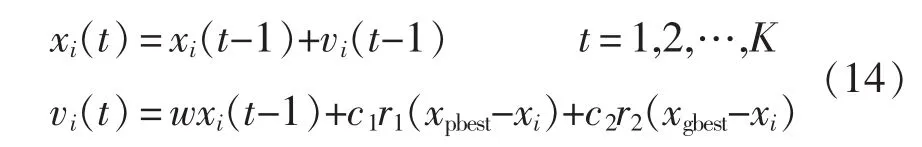
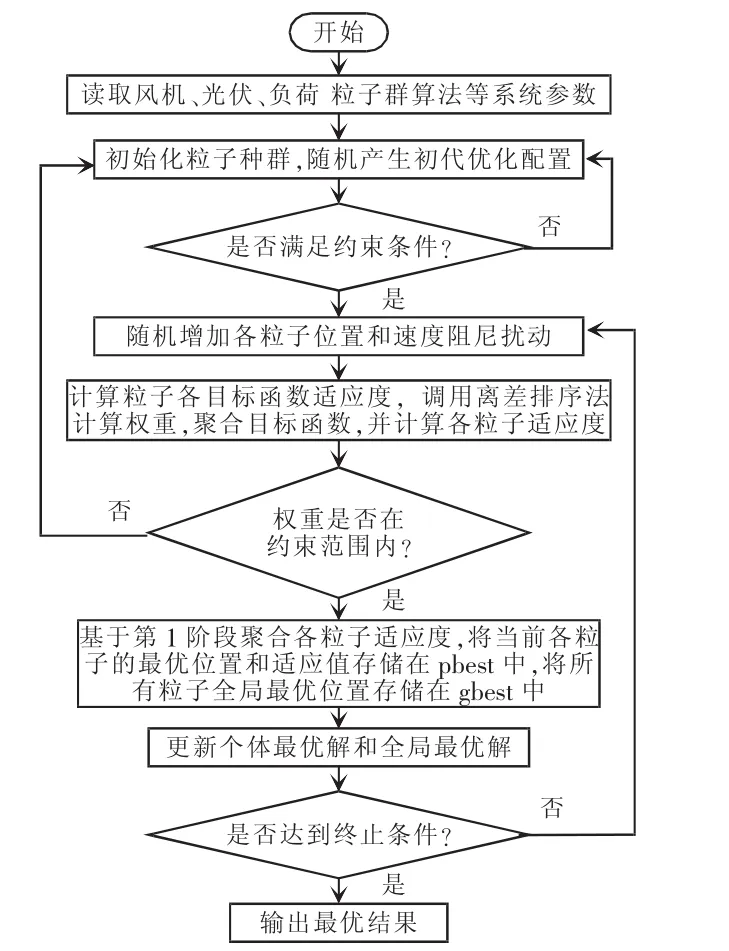
图2 优化模型求解流程Fig.2 Solving process of optimization model

式中：t为迭代次数，表示容量配置经过 t次更新；xi（t）为第t次更新后蓄电池和超级电容的配置结果；vi（t）为第t次的解与上一次解的差值。xpbest为第t次迭代为止的目前个体最优解；vxgbest为第t次迭代为止的目前总体最优解；w为惯性权值；c1和c2为加速因子；r1和r2为介于0和1之间的随机数；K为权衡最终解的精度和计算复杂度后确定的迭代次数。

步骤7最后判断迭代次数是否达到K值。若未达到K，回到步骤3继续执行；若达到K，搜索停止，输出蓄电池和超级电容优化配置的最优解，即

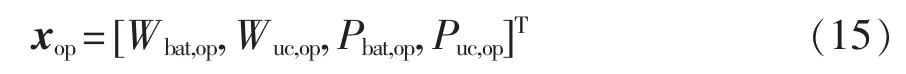
式中：xop为迭代K次后的最优解；Wbat,op为最优解中蓄电池能量最优值；Wuc,op为最优解中超级电容的能量最优值；Pbat,op为最优解中蓄电池功率最优配置；Puc,op为最优解中超级电容功率最优配置。

步骤8根据混合储能控制策略，通过枚举法列举一系列滤波时间常数Tr，循环操作以上步骤，最后通过总目标函数值评价帕累托边境值，从中找出最优解集。

3 算例分析

选取某示范微电网为设计案例，系统中的储能设备包括蓄电池和超级电容。使用HOMER仿真软件，观测步长为1 h的全年光伏、风电、负荷功率数据，结果如表1所示。独立系统的一个目标是满足供需平衡，因此需要计算供需不平衡功率。典型发电数据、负荷数据和供需不平衡功率如图3所示。

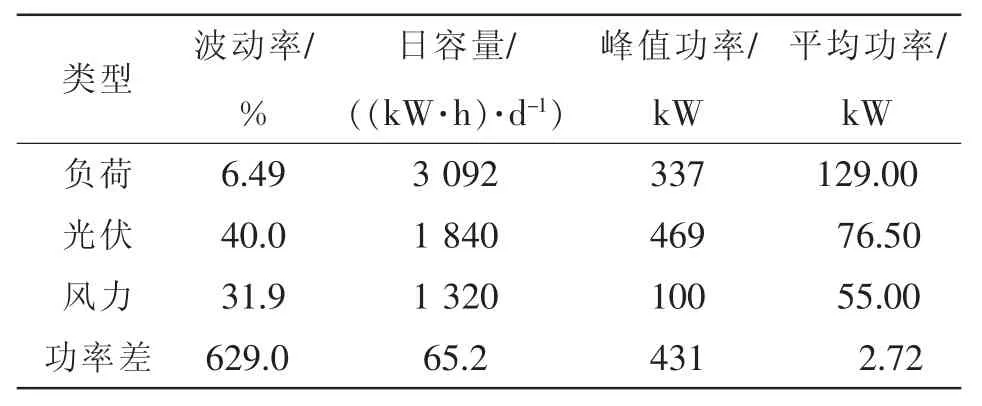
表1 分布式发电系统特征数据Tab.1 Characteristic data of distributed generation system

不平衡功率经低通滤波器滤波后，分解为高频和低频部分，分别由超级电容和蓄电池平抑。低通滤波器的时间常数分别取0.15 h、0.25 h、0.35 h和0.45 h，经过混合储能系统平抑后，不平衡功率波动及经低通滤波器后的超级电容和蓄电池功率波动曲线如图4所示。

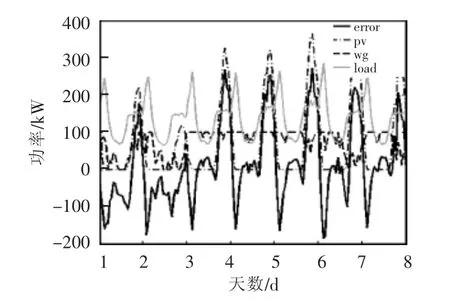
图3 典型功率波动曲线Fig.3 Typical power fluctuation curves

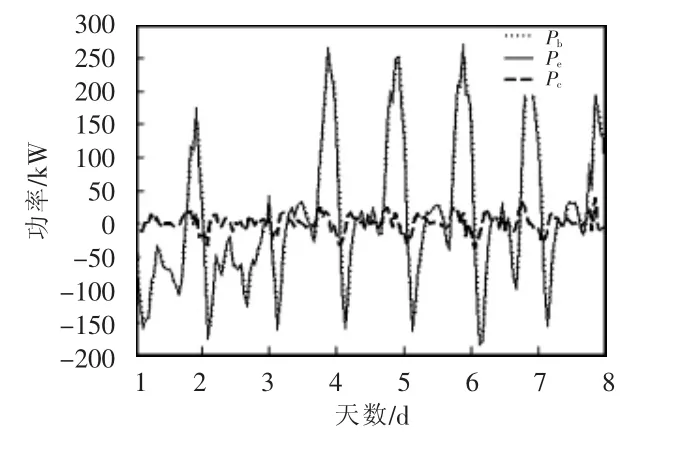
图4 超级电容和蓄电池功率波动曲线Fig.4 Power fluctuation curves of super capacitor and storage battery

低通滤波器将不平衡功率的高频波动部分分解出来，使铅酸电池承担的功率变得平滑，避免了铅酸蓄电池频繁充放电，延长了铅酸蓄电池寿命。而超级电容以超高充放电次数、超快充放电能力著称，因此分解出来的低峰值、高频率的波动量由超级电容平抑。

由上述混合储能多目标配置模型，首先确定优化配置中所需的最小储能容量和功率等约束条件，设备参数如表2所示。采用文中提出的优配置化算法迭代寻优，粒子群算法的种群数量为40；最大惯性权重为0.9；最小惯性权重为0.4；学习因子为2.0；最大迭代次数取为70。

经过粒子群算法得到最优配置结果，如表3所示。同时如图5展示了以成本适应度值为纵坐标的最优目标收敛曲线。从图中可以看出，求解算法可以快速收敛，年均总成本收敛于 74.2万元，对应的电池储能额定功率和额定容量分别为 60.8 kW和110 kW·h，超级电容的额定功率和额定容量分别为16.6 kW 和 1 kW·h。

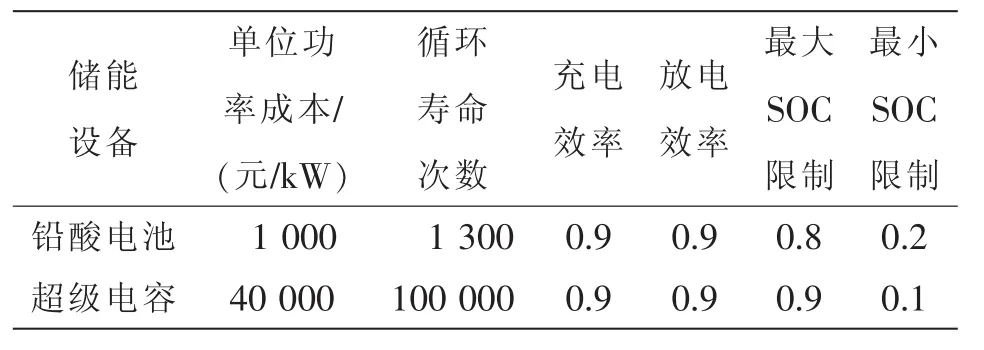
表2 混合储能设备参数值Tab.2 Parameter values of mixed energy storage equipment

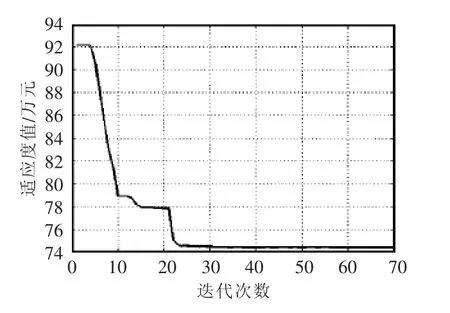
图5 最优目标收敛曲线Fig.5 Convergence curve of optimal objective

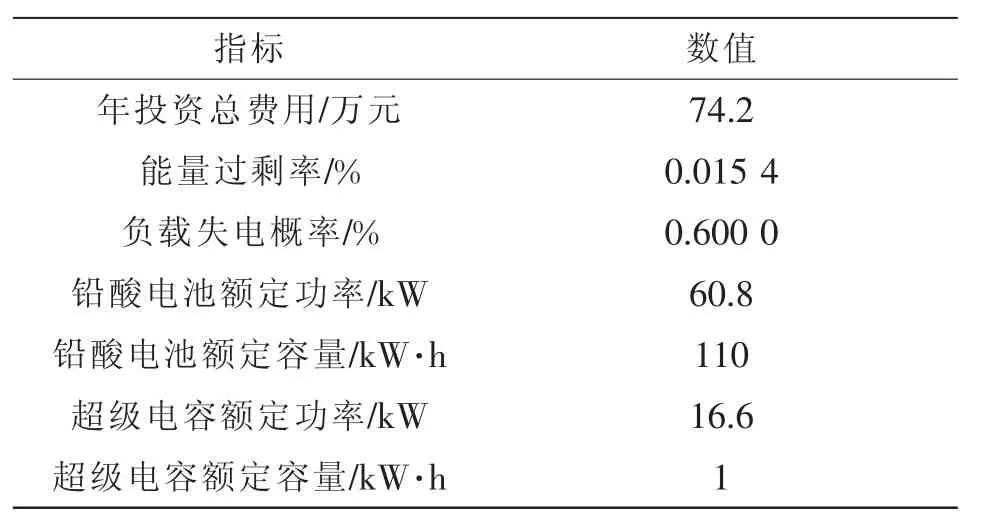
表3 混合储能最优配置结果Tab.3 Optimal allocation results of hybrid energy storage

4 结语

本文提出了一种用于混合储能系统平抑分布式发电功率波动的功率和容量优化配置方法。该配置方法以经济成本、供电可靠性、能量过剩和供需平衡为目标，以蓄电池SOC、超级电容端电压和最大功率为约束，同时考虑能量控制策略的影响，基于风光分布式发电数据，给出了最佳混合储能组合为电池功率/容量为配置结果。通过仿真验证了本文求解算法具有较快的收敛性。