并网逆变器系统的谐振抑制研究综述

黄亚申 ，汪海宁，马志保，杜 燕

（1.合肥工业大学教育部光伏系统工程研究中心，合肥230009；2.合肥聚能新能源科技有限公司，合肥230000）

能源与环境问题日益突出，近十年来，光伏发电、风力发电等可再生能源发展迅速，分布式发电系统受到广泛关注，成为近年来研究的热点[1-2]。随着分布式发电系统渗透率的不断提高，单一逆变器的容量已难以满足并网规模的需求，而多个逆变器并联共同组成的并网发电系统，成为分布式发电大规模应用的标志。并网逆变器作为可再生能源发电接入电网的关键设备，其性能好坏直接影响到整个并网发电系统。然而，并网逆变器中常用的脉宽调制PWM（pulse width modulation）技术给并网电流带来大量的开关次高频谐波，影响接入公共电网的敏感设备。早期的逆变器采用L和LC滤波器改善入网电流的质量，并已有较为成熟的研究成果[3-4]。在中高功率应用场合，增加滤波电感的方式虽然可以增强谐波衰减能力，但是降低了系统的动态性能，并带来元件体积过大、成本过高等一系列问题[5]。

针对L滤波器的不足，Lindgren在文献[6]中提出用LCL滤波器代替L滤波器进行滤波。与L滤波器相比，在相同的滤波效果下，LCL滤波器只需要较小的总电感，因此被越来越多的应用到并网逆变器中[7]。然而，LCL滤波器作为欠阻尼三阶系统，不可避免地为系统带来了谐振问题，如果直接使用传统的并网电流闭环控制方式，会影响并网逆变器控制的稳定性。此外，多逆变器并网系统中逆变器与逆变器之间、逆变器与电网之间的交互耦合等因素组成更为复杂的高阶谐振网络，进一步影响并网系统的稳定性。因此，采取有效的谐振抑制方法极为重要。纵观国内外已有文献，并网逆变器系统的谐振抑制方法主要分为单机型和多机型。根据逆变器自身的谐振特性，单机型又主要分为两种谐振抑制方法：一种是在滤波元件上直接串/并联电阻的无源阻尼方法，另一种是在控制中通过算法实现阻尼谐振的有源阻尼（active damper）方法。多机型则针对整个并网系统，通过建立精确的多逆变器并网系统模型，分析多机间的谐振交互机理，据此提出具有全局性特点的谐振抑制方法。

本文通过对国内外并网逆变器系统谐振抑制方法的研究现状及研究成果进行梳理和综述，分析不同谐振抑制方法存在的优点和不足，为多逆变器并网系统谐振抑制的深入研究提供参考。

1 并网逆变器系统建模与谐振机理

1.1 多机并网系统建模

随着分布式能源发电渗透率的不断提高，越来越多的电站使用多逆变器并联入网的系统结构。因此，本文对更加符合实际的包含多个单逆变器模型的典型多机并网系统进行建模，如图1所示，该系统由N个带LCL输出滤波器的逆变器在公共连接点PCC（point of common coupling）并联组成。每个LCL滤波器均由逆变器侧电感L1k、滤波电容Ck和网侧电感 L2k组成（k=a，b，c）。

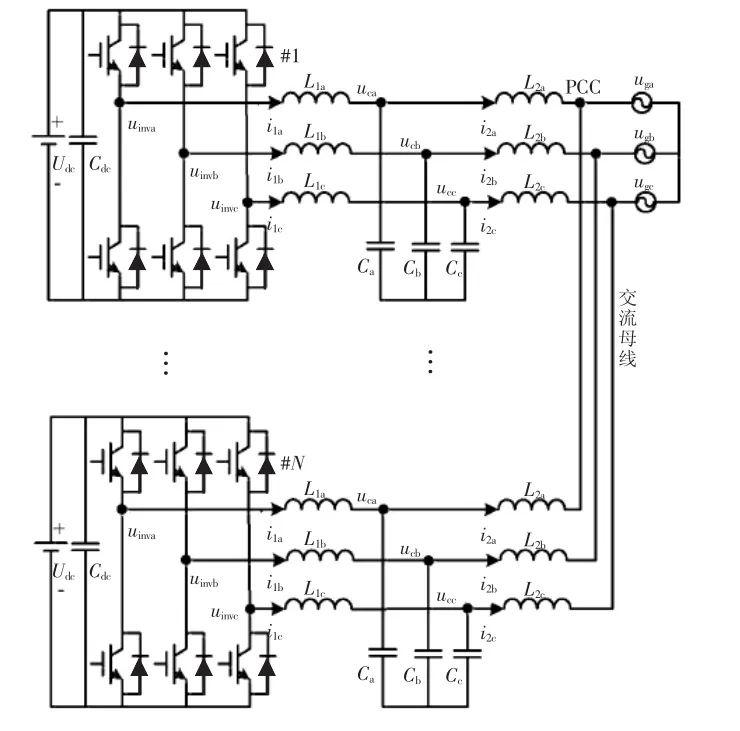
图1 典型LCL滤波的多逆变器并网系统结构Fig.1 Typical structure of grid-connected multi-inverter system with LCL filter

目前关于多逆变器并网的谐振研究大都集中于建立精确的多机并网模型，实现对其谐振机理的分析。文献[8]将多逆变器等效为多LCL并联的无源网络模型，以此分析并网系统的谐振现象。然而该无源网络模型没有考虑逆变器控制回路对系统的影响，不能准确反映实际系统的谐振特性。因此，文献[9-10]将包含逆变器控制回路的并网逆变器等效为由一个受控电流源并联一个等效输出阻抗的诺顿等效电路，电网侧等效为一个电网电压串联电网阻抗的戴维南电路，如图2所示，并将该模型用于研究逆变器自身影响、逆变器的交互影响以及电网电压的影响。为进一步提高模型精确性，文献[11]将逆变器数字控制非同步以及载波非同步考虑在内，建立了相应的小信号模型，而文献[12]将功率器件的死区效应以及非理想特性增加到等效模型中。

1.2 并网系统谐振机理

基于LCL滤波的单并网逆变器作为多逆变器并网系统的组成单位，其稳定运行是整个并网系统稳定运行的基础，事实上多数文献研究的也是如何消除单逆变器并网系统的谐振。因此，对谐振机理的分析分为两部分：即单逆变器并网谐振机理以及多逆变器谐波交互谐振机理。

1.2.1 单逆变器并网谐振机理

LCL滤波器作为欠阻尼3阶系统，是谐振产生的根本原因。图3为LCL滤波器的模型框图，由于三相对称，讨论时忽略三相符号k。

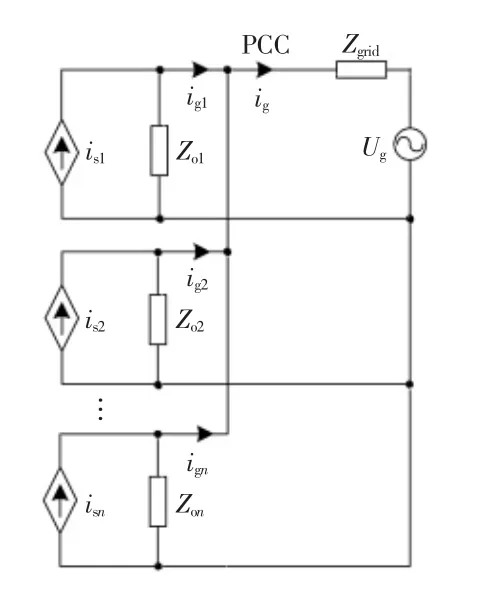
图2 多逆变器并网系统的等效模型Fig.2 Equivalent model of grid-connected multi-inverter system

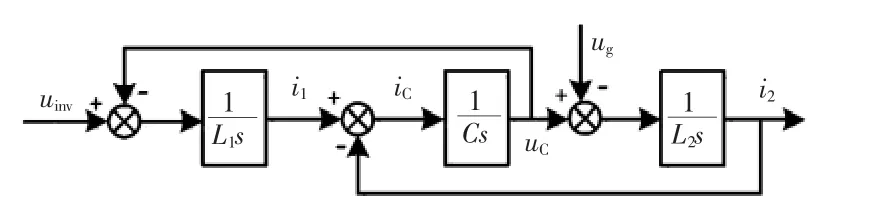
图3 LCL滤波器的模型框图Fig.3 Block diagram of LCL filter

根据图3可推导出桥臂输出电压uinv到逆变器侧电流i1和并网电流i2的传递函数分别为

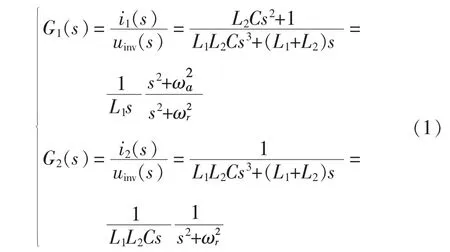
其中：

式中：ωr为LCL滤波器的谐振角频率；ωa为反谐振角频率。

图4 为 G1（s）和 G2（s）传递函数波特图，从图中可以得知：LCL滤波器在谐振角频率ωr处存在谐振尖峰，相位发生-180°跳变，从控制的角度讲，这个-180°跳变为一次负穿越，它会产生一对右半平面的闭环极点，导致并网逆变器不能稳定运行[13]。而反谐振角频率ωa处存在负谐振尖峰，对此处的高次谐波具有很大的衰减作用，不影响系统稳定性。

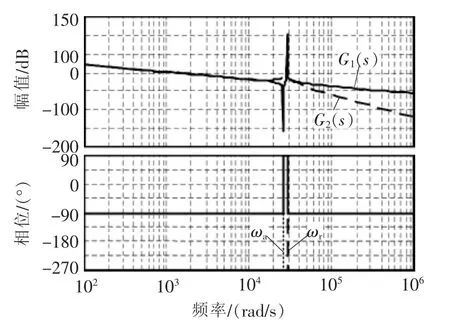
图4 LCL滤波器的波特图Fig.4 Bode diagram of LCL filter

1.2.2 多逆变器谐波交互谐振机理

在弱电网情况下，各并网逆变器并联在PCC点，经过一定的电网阻抗与电网相连，研究表明，多逆变器之间正是通过电网阻抗产生交互影响[14]。从阻抗分析的角度出发，在某一频率处，当逆变器侧阻抗与网侧阻抗大小相等而相位相差180°时，若有频率匹配的谐波激励源，系统最容易出现谐振现象[15-16]。若逆变器系统产生的谐波电流频率或者电网中的谐波电压频率接近或等于阻抗网络谐振频率，可分别导致系统出现并联谐振和串联谐振[17]。基于上述阻抗网络模型的谐振机理研究重点包括并联逆变器台数和电网阻抗变动对系统谐振特性的影响。其中，多逆变器之间的交互作用往往会耦合出新的谐振点，随着逆变器数量的增加，新的谐振点会向低频移动，并且谐振峰值有所降低，如图5所示。由于阻抗网络结构的改变，电网阻抗对N台逆变器中的某一台来说等效增大为原来的N倍，该特性对系统控制器的设计有一定参考作用[14,18]。上述研究均基于各并网逆变器软硬件参数相同的条件，当不满足该条件时，谐振机理的分析会更加复杂[19]。

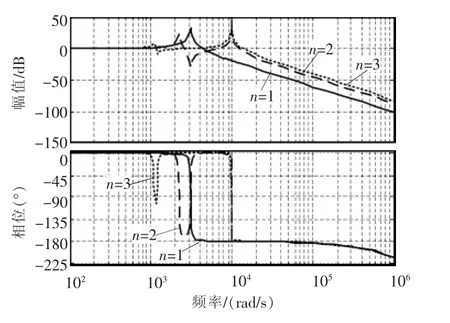
图5 多逆变器间的谐波交互谐振特性Fig.5 Interactive resonance characteristics among multiple inverters harmenic

2 单机型谐振抑制研究

2.1 基本的无源阻尼

由前述可知，系统欠阻尼是谐振产生的根本原因，因此首先提出的谐振抑制方法是在滤波元件上串/并联电阻的无源阻尼方法。该方法简单直接地增加了系统阻尼，不需要增加传感器，也不需要改变控制算法[7]。文献[20-21]基于LC滤波器的谐振问题，分别在滤波电感L和滤波电容C上串/并联电阻实现了谐振抑制。因此，在LCL滤波器的3个滤波元件上分别串/并联电阻，可以得到6种无源阻尼的方式，如图6所示。

根据图6可推导出每种无源阻尼方式下入网电流i2与逆变器侧电压uinv的传递函数G2d（s）。为了直观地观察每种阻尼方式对谐振的抑制效果以及对系统谐波衰减的影响，定义

式中，K为增加阻尼电阻后各频率段谐波幅值的相对增益。以滤波电容串联电阻Rd为例，则有

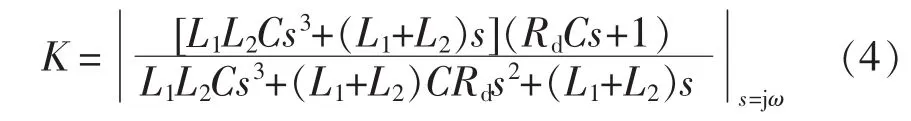
式（4）中起到谐振阻尼作用的主要是（L1+L2）CRds2项。根据式（4）可以绘出K、Rd和频率三者关系的三维图，如图7所示，图中Zc为谐振频率处电容容抗。

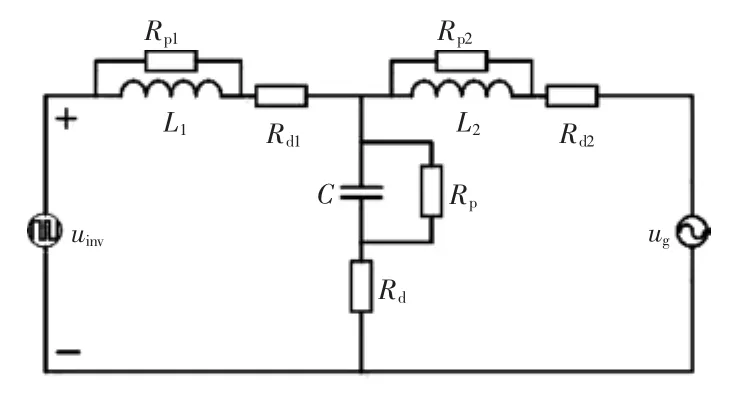
图6 基本的无源阻尼方式Fig.6 Basic passive damping methods

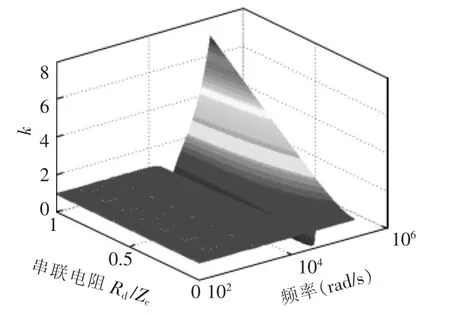
图7 滤波电容串联电阻时各谐波幅值相对增益Fig.7 Relative gain of harmonics with serial resistor

由图7可见，串联电阻Rd对低频段几乎没有影响。随着Rd增大，在谐振频率处沟壑越深，表示抑制谐振的效果越好；而在高频段，随着Rd增大，K越大，谐波衰减能力越弱。

利用相同的分析方法可以发现，每种无源阻尼方式除了能阻尼谐振外，还有如下特点[22]：

（1）滤波电感（包括逆变器侧滤波电感L1和网侧滤波电感L2）串联电阻可以保持系统的高频衰减特性基本不变，却降低了其低频增益，影响系统稳态控制性能。

（2）滤波电感并联电阻对系统低频增益影响较小，但是会削弱系统的高频衰减能力，无法兼顾阻尼和滤波特性。

（3）滤波电容并联电阻不改变系统低频和高频频率特性，需要较大的阻尼电阻才能明显抑制谐振峰。此外阻尼电阻所承受的电压接近电网电压，会带来较大的功率损耗。

（4）滤波电容串联电阻会影响系统高频衰减能力，但当阻尼电阻与电容容抗相比较小时，就能明显抑制谐振峰，此时对高频段衰减速率影响有限，功率损耗也较小。

综上所述，从阻尼特性、控制特性、滤波特性以及功率损耗的角度综合分析，滤波电容串联电阻的方案的综合性能优于其他5种，实际工程中一般采用此种无源阻尼方式。

2.2 改进的无源阻尼

为进一步减小阻尼电阻的功率损耗，改善对高频谐波的衰减能力，在电容串联电阻的基础上，文献[23-24]提出了一系列改进的措施，如图8所示。

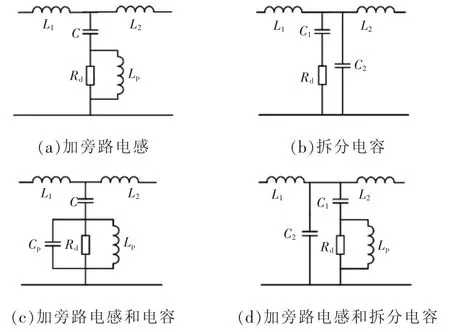
图8 4种改进的无源阻尼方法Fig.8 Four improved passive damping methods

上述4种改进的无源阻尼方法主要思路是利用电感和电容在低频和高频不同的阻抗特性，分别为低频和高频谐波电流提供低阻尼通路。

（1）利用加旁路电感在低频段的感抗远小于串联电阻的阻值的特点，实现对串联电阻的旁路，减小了低频谐波电流在串联电阻上的功率损耗，但是不能改变LCL滤波器在高频段的频率特性。

（2）加拆分电容或旁路电容提高了对高频谐波的衰减能力，这是因为低阻尼的高频通路吸收了大部分的高频谐波电流，但是难以减小低频谐波电流在串联电阻上的功率损耗。

由此可见，图8（a）和图8（b）所示这两种方法分别只实现了减小功率损耗和提高对高频谐波衰减能力，而图8（c）和 8（d）这两种方法则结合了旁路电感和旁路电容（或拆分电容）的优点，不仅实现了较强的高频谐波衰减也减小了串联电阻的损耗，增强了系统的稳定性，非常适用于兆瓦级别的并网逆变器[24]。然而，无源元件数量和种类的增加，不仅提高了系统的成本和体积，也增加了电路的复杂性和不确定性，极大地限制了这些改进措施的应用范围。

2.3 单电流闭环控制的稳定性分析

单电流闭环控制主要以控制简单和成本最小为目的，对其稳定性进行分析必不可少，主要包括逆变器侧电流控制和并网侧电流控制。图9为单电流闭环反馈的控制框图，图中，Gc（s）为电流调节器，Gd（s）=kPWMe-1.5Tss，其中：kPWM为逆变桥放大倍数；Ts为采样周期；e-1.5Tss为系统延时、包括采样保持延时、计算延时以及PWM装载延时。

“互联网+教育”脱离传统课堂，增强了学生学习的自主性。首先在教学资源上，学生可以按自己的需要直接在网上搜索。其次在教学模式上，在线学习、互动学习成为主流，改变了传统教育中以教师在课堂教授为主的模式[3]。最后在教学形式上，没有时间和地点的限制，学生可以根据自己的实际情况进行复习和回顾。

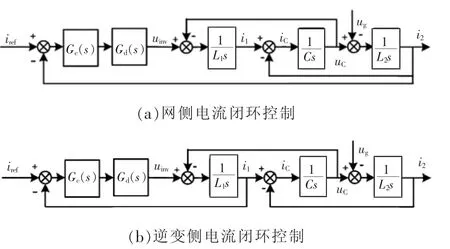
图9 单电流闭环控制框图Fig.9 Block diagram of single-current closed-loop control

以网侧电流反馈为例，系统在s域中的开环传递函数为

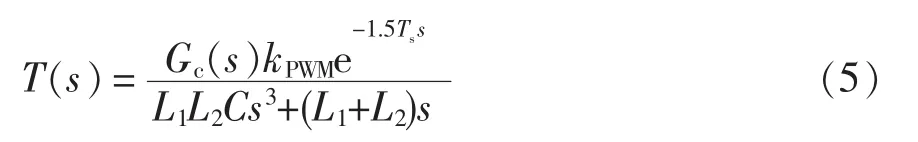
由于T（s）中含有非线性环节e-1.5Tss，无法直接求取系统的闭环零极点，因此需推导出T（s）在z域的表达式，即

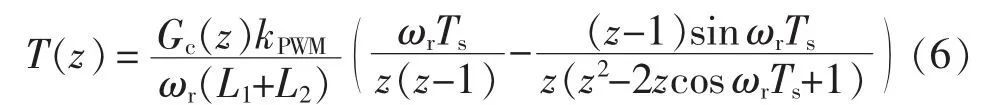
图10是根据式（6）得到的上述系统闭环零极点分布。使用网侧电流闭环控制时，在采样频率小于fA的频率范围内，系统的闭环极点均位于单位圆内，系统是稳定的；反之，闭环极点位于单位圆外，系统不稳定。使用逆变器侧电流闭环控制时，当采样频率大于fB时系统稳定，否则系统不稳定。可见单电流闭环控制系统的稳定性与电流反馈点及采样频率大小有关。文献[25]进一步指出，系统稳定与谐振频率和采样频率的比值有关，比值越大越有利于并网电流反馈系统的稳定，反之越有利于逆变器侧电流反馈系统的稳定，但并没有给出谐振频率与采样频率比值的临界值，使得在已知谐振频率和采样频率的情况下不能确定采用何种电流反馈方式。文献[26]在考虑计算延时和PWM装载延时等1.5倍采样周期延时的基础上，计算出该临界值为1/6。当两者比值大于该临界值时，使用并网电流反馈可以使系统稳定，反之则反馈逆变器侧电流。

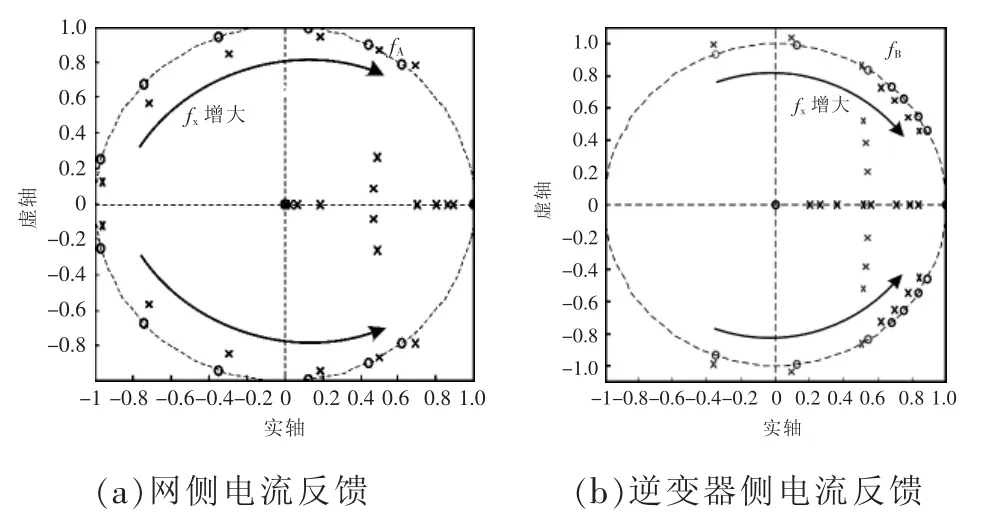
图10 采样频率变化时单电流反馈系统闭环零极点分布Fig.10 Closed-loop pole-zero distribution of singlecurrent feedback system at varying frequency

然而，由于没有对谐振峰进行大幅度的抑制，导致并网电流中谐振频率处的谐波含量较大。在弱电网中，电网阻抗变动范围较大，系统的谐振频率也会随之变化，可能导致系统失稳，难以保证系统的鲁棒性[27]。

2.4 有源阻尼方法

通过研究已有的文献，本节按照不同的有源阻尼思想将现有的方案分为以下3种进行分类和评述：即基于滤波器与电流调节器级联的有源阻尼、基于系统降阶的有源阻尼以及基于状态变量反馈的有源阻尼。

2.4.1 基于滤波器与电流调节器串联的有源阻尼

在包含电流控制器的前向通道上串联一个滤波器，利用该滤波器特有的相位特性或者幅值特性改变原系统的开环幅频响应，达到使系统稳定的目的，是该类有源阻尼方法的基本思想。其控制结构简单且不需要额外的传感器[28]，具有易嵌入和物理意义明确的特点。控制框图如图11所示，Gn（s）为滤波器的传递函数。

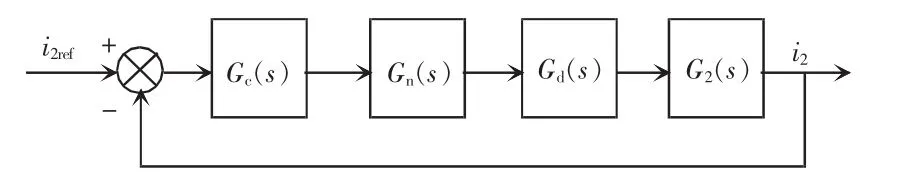
图11 基于滤波器与电流调节器串联的有源阻尼方法Fig.11 Active damping method based on filter in series with current regulator

已有文献将此滤波器的种类主要分为低通滤波器、超前-滞后补偿器以及陷波器。图12为系统开环传递函数波特图，无串联滤波器时，系统的穿越频率在谐振频率ωc1处，由于幅值裕度GM1＞0 dB,此时系统是不稳定的。串联低通滤波器后，其相位滞后特性将穿越频率向低频转移到ωc2，此时GM2＜0 dB，系统可以稳定运行，同时也增强了对高频谐波的衰减能力。但是也带来系统相位裕度降低的不利影响，即PM2＜PM1。超前-滞后补偿器则主要利用相位超前特性将穿越频率向高频移出谐振不稳定范围。然而文献[29]指出其相位超前不足以将穿越频率移出增益大于0 dB的谐振频率范围，实际使用中并不采用此方式。

陷波器方式是3种方式中最灵活有效的，该方式通过在谐振频率处产生一个负谐振峰抵消系统原谐振峰，将穿越频率处的增益降低到0 dB下以确保系统稳定。为了减小计算量和控制复杂度，一般使用二阶陷波器，其传递函数为

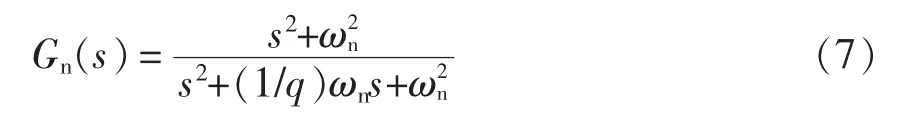
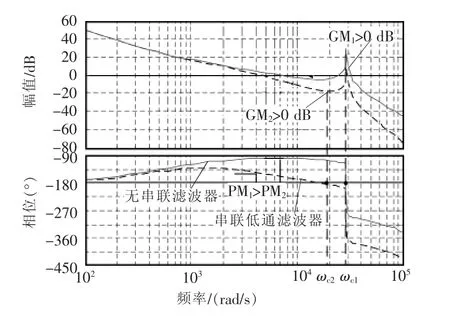
图12 串联低通滤波器时系统开环传递函数频率特性Fig.12 Frequency characteristics of system’s open-loop transfer function with low-pass filter in series

2.4.2 基于系统降阶的有源阻尼

LCL滤波器作为一个3阶网络，具有谐振现象是其固有属性。采用合适的控制策略将系统降阶以避免谐振的出现成为解决谐振问题的另一个方案。文献[32-33]对LCL滤波电路进行了改变，将滤波电容C按比例分裂为并联的两部分，取两电容的中间电流作为反馈量，如图13所示。图中，L1/L2=α/（1－α），C1/C2=β/（1－β），且 α=L1/（L1+L2），β=C1/（C1+C2）,显然 0＜α＜1,0＜β＜1。此时逆变器输出电压 uinv到中间电流反馈量i12的传递函数为

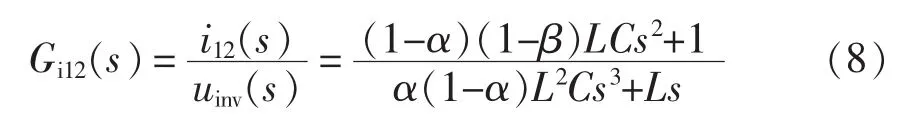
图13 分裂电容法电容中间电流反馈控制系统Fig.13 Feedback control system of capacitor current by splitting the capacitor of LCL filter

式中：L=L1+L2；C=C1+C2。当满足 β=1－α，即 C1/C2=L2/L1时，式（8）中的 Gi12（s）将变为一阶系统，即

实现了对系统的降阶，避免了电容中间电流出现谐振。上述系统中电容中间电流i12实质上是逆变器侧电流i1和并网电流i2的加权电流值，与文献[34]中的加权平均电流反馈控制相同，即

分裂电容法将原系统分成了2个串联的谐振电路，没有对并网电流直接控制，使并网电流中依然存在谐振[35]。此外，实际使用中滤波元件的参数可能会出现变化，难以完全按照权重系数的比例进行分配，影响系统降阶，导致这两种方法的鲁棒性不足。

文献[36]利用网侧电流反馈（或逆变器侧电流反馈）和一种状态量前馈解耦实现了系统的另一种降阶方式。不考虑系统延时，此时 Gd（s）=kPWM，以网侧电流i2反馈和逆变器侧电感电压uL1前馈为例，其控制框图如图14所示。

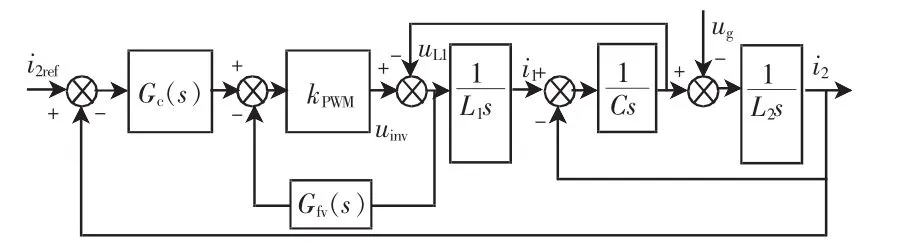
图14 网侧电流反馈与逆变器侧电感电压前馈相结合的控制策略Fig.14 Control strategy of grid-side current feedback combined with inverter-side inductive voltage feedforward

可得系统的开环传递函数为

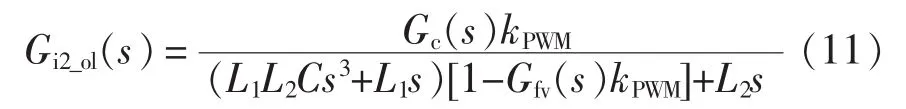
当前馈传递函数 Gfv（s）=1/kPWM时，式（11）变为

可以看出，不考虑电流调节器Gc（s）时，系统降为了1阶。该方案不仅摆脱了对滤波器参数的依赖，同时也实现了对并网电流的直接控制。由于没有考虑控制延时的存在会影响系统降阶的效果，文献仅进行了仿真验证。

2.4.3 基于系统状态变量反馈的有源阻尼

对于系统状态变量反馈实现抑制谐振的原理可以从两个角度解释：第一个角度是，系统中间状态变量中含有谐振电压或谐振电流的信息，反馈这些状态量可以消除谐振分量的激励源，从而防止谐振出现；另一个角度是，通过反馈状态变量来虚拟无源阻尼中串联或并联的电阻，这种“虚拟电阻”法物理意义明确，易于理解。通过对典型反馈控制系统的研究，文献[44]指出了状态变量反馈抑制谐振的本质原因，即在谐振频率处对系统状态变量进行负反馈控制即可实现较好的峰值抑制效果。

在无源阻尼方法中，滤波电容两端并联电阻的方式具有不改变系统低频和高频特性的独特优势，其控制框图如图15（a）所示。经过框图等效变换，可以得到基于电容电压一次微分反馈[25]、并网电流二次微分反馈[37]和滤波电容电流比例反馈[38-40]的有源阻尼方式，分别如图15（b）、（c）、（d）所示。

图15（b）、（c）的方式虽然具有等效的电容并联电阻，但在实际应用中，微分会放大高频噪声，且理想的微分难以实现。相比之下，图15（d）所示的电容电流比例反馈简单易实现。此外，还有文献研究了全状态变量反馈[41]以及众多改进的有源阻尼方法[42-43]。

鉴于电容电流比例反馈有源阻尼方法的软件易实现性，以及网侧电流反馈可实现单位功率因数控制的特性，近年来，在关于并网逆变器谐振抑制的文献中使用最多的是电容电流比例反馈和并网电流反馈的双环控制策略[45-46]，如图16所示。

与其他有源阻尼方法相比，双环控制方法除了控制器参数、反馈系数易于设计外，在环路增益、动态响应、稳定裕度等方面都具有更优秀的表现[47]，尽管如此，该谐振阻尼方案仍需改进。文献[48]指出在考虑计算延时和PWM调制延时的情况下，原来的虚拟电阻不再等效为一个纯电阻，而是一个与频率相关的阻抗，如图17所示。当谐振频率高于1/6倍的采样频率时，该阻抗表现为负阻特性，导致电流控制性能和系统对电网阻抗变化的鲁棒性降低。为此，该文献提出了电容电流即时采样方法，以减小电容电流反馈中的计算延时。文献[49]提出的双采样模式实时运算方法则完全消除了计算延时，进一步提高了系统的鲁棒性和电流控制性能。

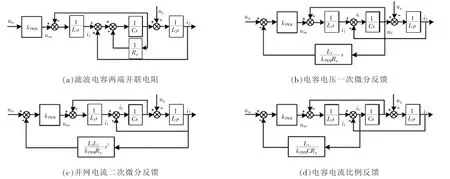
图15 基于状态变量反馈的等效有源阻尼方法Fig.15 Equivalent active damping methods based on feedback of state variables

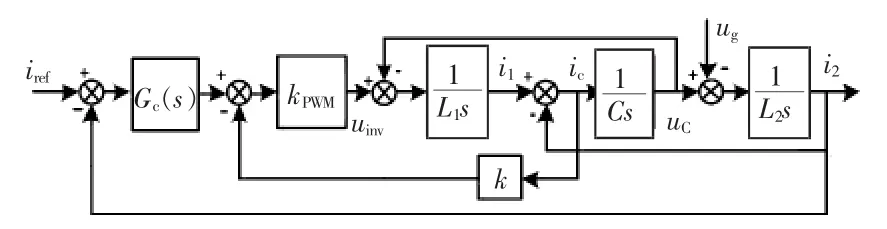
图16 电容电流比例反馈和并网电流反馈的双环控制Fig.16 Dual-loop control of capacitor current proportion feedback and grid-side current feedback

图17 考虑控制延时的等效阻抗Fig.17 Equivalent impedance with the consideration of control delay

3 多机型谐振抑制研究

并网系统谐振特性的改变，使得单台谐振抑制良好的逆变器并联以后仍然会遇到稳定性问题[50]。本文将多机并网系统的谐振抑制方法归纳为两类进行阐述，一类是以虚拟谐波阻抗 （virtual harmonic impedance）为代表的谐波源消除法，另一类是在PCC点加装谐振抑制单元改变谐振网络特性的阻抗重塑法。由于两者均需检测PCC点电压并作用于整个系统因而具备全局性特点。

3.1 谐波源消除法

由多机并网系统谐振产生机理可知，系统出现串联谐振和并联谐振均是因为有频率相匹配的谐波源激励。因此，消除谐波源可以避免其进入谐振网络，实现谐振的抑制。文献[10]将虚拟谐波阻抗与改进无差拍控制结合，从逆变器并网电流的指令中消除谐波进而实现对谐振的阻尼。该方法虽然等效于在滤波电容两端并联电阻，但又不同于单个逆变器实际并联电阻的无源阻尼或者并联虚拟电阻的有源阻尼，前者只对电流谐波分量产生阻尼，而不影响基波分量的流动。其控制框图如图18所示。

虚拟谐波阻抗法使用谐波检测器检测滤波电容电压（或PCC点电压），并将谐波电压与基波电压分离，随后通过一个虚拟电阻产生谐波电流参考，将其叠加到无差拍控制器的输入中。改进无差拍控制表示为

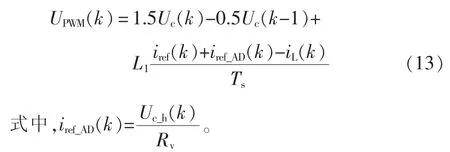
该方法只需要改进控制算法而不需要附加额外的硬件装置和传感器，因而具有成本优势。

文献[51]提出的有源谐波电导法与上述虚拟谐波阻抗法原理相同，其结构等效于在滤波电容两端并联一电导，供谐波电流流通，防止其流入谐振网络产生谐振。该方法同样需要从电容电压中分离谐振电压分量，再经过电导获取谐波电流参考，不同点在于电流调节使用的是PI控制器。由于谐振频率一般较高，对电流的跟踪需要高带宽的电流控制器，无差拍控制器自身的高带宽特性容易满足此要求，而PI控制器设计时则要兼顾动态性能与系统稳定性。

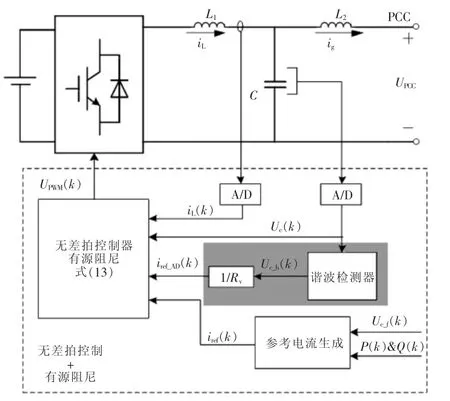
图18 基于无差拍控制的虚拟谐波电阻结构Fig.18 Structure of virtual harmonic resistor based on deadbeat control

3.2 阻抗重塑法

通过阻抗重塑使逆变器输出阻抗和电网阻抗没有交点或者将交点向更高频移动，破坏谐振形成条件，是解决多机并网系统谐振问题的另一个途径[52]。一种方式是在PCC点加装谐振抑制单元，即检测并网点电压获取谐振频率，并在谐振频率处辅以一定的阻尼系统，实现对谐振的系统级抑制，但是基于该思想的方法对谐振频率的检测有较高的要求。文献[53]在PCC点安装3个由电阻、电感和电容串联组成的陷波器，其中电感和电容均是可调的，3个无源元件的参数根据PCC点谐振频率进行配置。该无源陷波器的结构如图19所示。

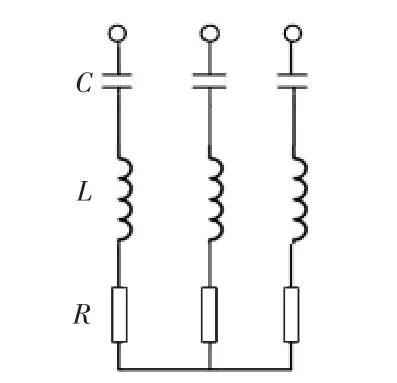
图19 无源陷波器的配置Fig.19 Configuration of passive notch filter

谐振抑制装置的等效阻抗

式中，ωr为PCC点电压谐振频率。配置电感和电容的参数使等效阻抗中的电抗为0，使其在谐振频率处以阻性为主，增加了逆变器输出阻抗。实际上，由于电阻阻值往往较小，谐振抑制装置对特征次谐波（如谐振处谐波）构成了低阻尼通路，对大部分特征次谐波实现了分流，从而起到了抑制谐振的作用。文献[54]用3个并联的3阶高通滤波器作为谐振抑制装置，参数配置原则与文献[53]相同。上述2种谐振抑制装置使用的均是无源元件，可靠性高，易于实现。然而无源元件的存在也会出现功率损耗大的不足，尤其当电阻较小时，该问题更为明显。

文献[55-56]在PCC点处使用的有源阻尼器是对上述不足的改进。如图20所示，小功率高开关频率变换器仅在谐振频率处对谐波进行补偿，引入等效阻尼电阻重塑逆变器输出阻抗，这一特点有别于传统有源滤波器APF（active power filter）对所有非基频谐波的补偿。有源阻尼控制器有两种实现方案，如图21所示。方案（a）检测PCC点谐振电压分量，经过等效电阻获取谐振电流参考；方案（b）则使用具有一定带宽的谐振电压控制器直接补偿谐振分量，谐振控制器表达式为

式中：Rd_e和Rdref分别为有源阻尼器模拟的实际电阻和参考电阻；ωc为谐振控制器的带宽；ωr为检测的谐振频率。谐振控制器的优点在于考虑了谐振频率变化时有源阻尼器的有效性，更加符合实际并网系统的运行情况。此外，上述两种方案均要求谐振频率的检测满足较高的精确性和快速性。

相比于无源谐振抑制装置，一方面，使用有源阻尼器虽然需要增加1台额外功率变换器的成本，但是随着电力电子器件相关技术的快速发展，其一次性成本较多的问题将会得到改善。并且从长远来看，由于不具有使用无源谐振抑制装置出现的功率损耗以及散热问题，使用有源阻尼器显然更为经济。另一方面，当谐振频率变化时，功率变换器特有的快速响应特性也优于无源谐振抑制方式通过传动装置进行的相对较慢的调节，极大降低了系统在过渡过程中出现谐振的风险。因此，未来的研究方向可放在探寻新型有源谐振抑制装置上。

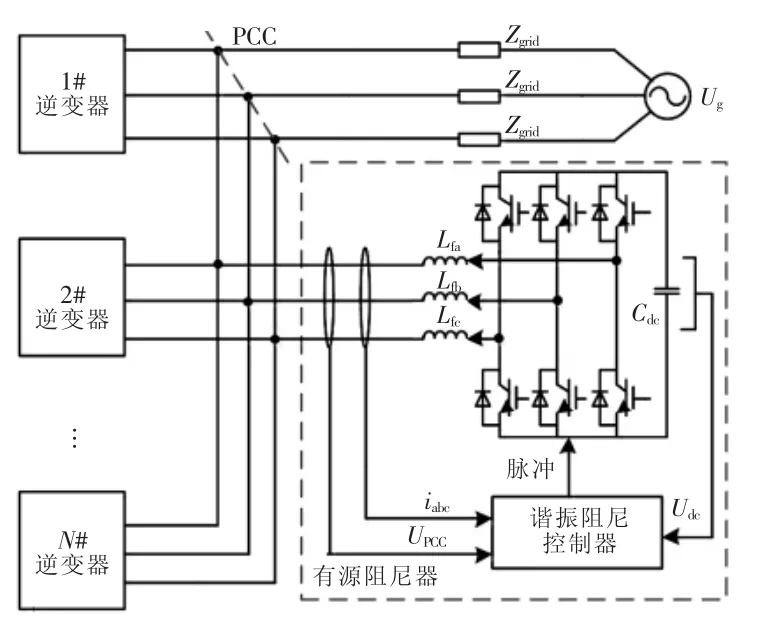
图20 有源阻尼器的基本配置Fig.20 Basic configuration of active damper

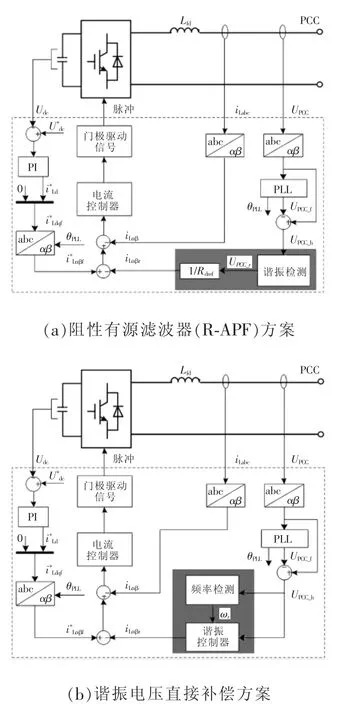
图21 有源阻尼器的两种实现方案Fig.21 Two implementation schemes of active damper

4 结论

本文针对并网逆变器系统出现的谐振问题，从单机型和多机型两个层级对国内外研究现状进行了归纳、总结。其中单机型主要包括无源阻尼和有源阻尼方法，多机型包括谐波源消除法和阻抗重塑法。结论如下：

（1）从阻尼特性以及控制复杂程度的角度考虑，滤波电容串联电阻是适宜实际工程应用的无源阻尼方式；从功率损耗的角度出发，结合旁路电感和旁路电容（或拆分电容）的无源阻尼方式更有利于减小功率损耗。

（2）电流反馈点以及采样频率和谐振频率的比值决定单电流闭环控制系统的稳定性。在三类有源阻尼方法中，利用串联滤波器的幅相特性改变原系统的开环幅频响应可以使系统稳定，但鲁棒性需要改进；以分裂电容法为代表的系统降阶方法，其有效性受滤波元件参数变动以及控制延时影响较大；基于电容电流反馈的双环控制策略等效于在滤波电容两端并联一个虚拟电阻，其不改变系统低频和高频特性的优势使其在有源阻尼中使用较多。

（3）多逆变器并网系统各逆变器之间通过电网阻抗产生谐波交互作用，耦合出新的谐振点。从阻抗分析角度分析了其谐振机理，并据此总结了谐波源消除法主要根据消除谐振激励源的思想抑制谐振，而阻抗重塑法通过在PCC点加装谐振抑制单元破坏谐振形成条件，达到消除谐振的目的，两者均具有全局性特点。

（4）目前单机型的谐振抑制研究为成熟，而多机型的研究略显不足，因此未来的研究方向应包括：建立更精确的多机并网模型、探寻新型具有全局性特点的有源谐振抑制策略以及在此基础上拓宽多机型谐振抑制的思路等方面。