基于加权Voronoi图和自适应PSO算法的电动汽车充换电站联合规划

董彦君 ，闫志杰 ，马喜平 ，刘丽娟 ，张蕊萍 ，董海鹰

（1.中国农业大学信息与电气工程学院，北京 100083；2.兰州交通大学自动化与电气工程学院，兰州730070；3.国网甘肃省电力公司电力科学研究院，兰州730050）

现如今，能源紧缺和环境污染问题日益严峻，节能减排越来越受到人们重视，电动汽车EV（electric vehicle）相较传统燃油汽车，具有能耗低、污染小等优点，具有良好的发展前景[1-2]。根据《“十三五”国家战略性新兴产业发展规划》，2020年和2030年我国电动汽车累计产销量将分别达到500万辆和6 000万辆[3]。电动汽车目前在我国仍处于示范推广阶段，且存在着电能补给设施与电动汽车发展不协调、政府配套支持政策不完善等问题，而建设便捷高效的电能补给设施是电动汽车普及的前提。所以为了满足电动汽车电能补给需求，有必要对电动汽车充、换电站进行合理规划。

文献[4]针对电动汽车类型多样性，提出一种计及不同类型电动汽车充电需求的充电设施规划方案；文献[5]研究了换电模式下电池组数量规划问题，将规划阶段分为远期和近期两个阶段，通过远期规划估算某一时段充电站需储备的电池数量，近期规划得到需要购买的电池数量和物流配送次数；文献[6]通过对城市道路交通情况分配权重来反映电动汽车的分布情况，建立了考虑电动汽车充电行为特点和充电站服务半径的多目标规划模型；文献[7]提出使用风电和光伏来为电动汽车充电站供电，从硬件组成和软件平台两个方面对充电站进行了设计；文献[8]给出了电动汽车充电需求分布的预测方法，采用Voronoi图划分充电站服务范围。以上文献主要是针对充电站的规划进行了研究，没有考虑到充、换电站的联合规划，且只采用Voronoi图等数学优化算法，无法保证所划分的服务范围达到最优。

本文针对当前电动汽车电能补给设施规划方面中存在的不足，提出一种充、换电站联合规划方法，建立了考虑用户和充、换电站运营商利益的充、换电站联合规划模型，运用加权Voronoi图和自适应粒子群优化算法结合对模型进行求解，通过算例验证了所提方法的可行性。

1 电动汽车充、换电站“集中充电、统一配送”运营模式

2011年国家电网公司发布了《“十二五”电动汽车充电服务网络发展规划》，提出了“换电为主、插充为辅、集中充电、统一配送”的商业运营模式，该运营模式包含换电、配送、充电三个方面。当用户发现电动汽车电量不足时，将车辆行驶至距离用户最近的电动汽车换电站，将电量即将耗尽的电池卸下，换上满电电池，整个换电流程耗时约5～10 min。换电站通过物流系统将每天换下的电池运送至充电站充电，充电站可建在靠近新能源发电站及变电站的郊区，同时充电站可选择在电力负荷谷时段对电池充电，保证经济性的同时又起到削峰填谷的效果。当电池充满电后，再通过物流系统将满电电池运送至换电站，满足换电站对电动汽车的换电需求。具体运营模式如图1所示。

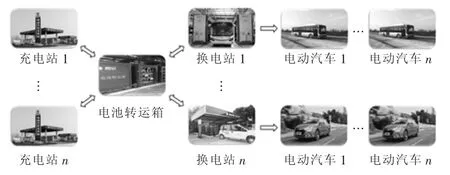
图1“集中充电，统一配送”运营模式示意Fig.1 Schematic of operation pattern of“Centralized charging and unified delivery”

2 电动汽车换电需求预测及充电站数量预估

2.1 电动汽车保有量预测

充、换电站规划首先要确定目标规划年各类型电动汽车保有量，根据基准年及目标规划年的传统汽车保有量，结合Bass扩张模型进行预测。Bass扩张模型是一种研究新产品在市场中扩张效果的预测模型，模型离散时间公式[9]为

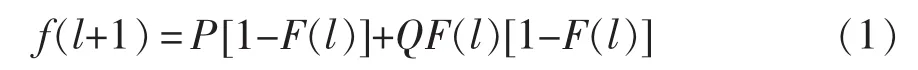
式中：f（l+1）为l+1时新购买用户数量占潜在用户数量的比例；F（l）为到l时累计购买用户数量占总潜在用户数量的比例；P为创新系数；Q为模仿系数。P和Q的取值是确定Bass模型的关键，当消费历史数据充足的情况下，可采用最小二乘法、极大似然法等计算出P、Q的值。但电动汽车在我国目前仍处于推广阶段，缺少相关数据，所以本文通过对传统汽车市场发展特性的分析，确定传统汽车市场发展Bass模型关键参数，并根据电动汽车的特性对其影响因素进行比较，来获得电动汽车的Bass模型关键参数，电动汽车的Bass模型参数为

式中：EVp、EVQ分别为电动汽车 Bass模型的 P、Q值；CVP、CVQ分别为传统汽车Bass模型的P、Q值；SEV为电动汽车内、外部影响得分；SCV为传统汽车内、外部影响得分。

电动汽车Bass模型参数影响因素见表1。

表1 电动汽车Bass模型参数影响因素Fig.1 Influencing factors of parameters in Bass model of EVs

假设传统汽车数量每年增长率为10%，电动汽车潜在数量占每年新增汽车销量的80%，则电动汽车保有量为

式中：Nev为电动汽车至目标规划年总保有量；ΔNcv为每年传统汽车增长量。

2.2 电动汽车总换电需求

（1）各类型电动汽车日电量需求为

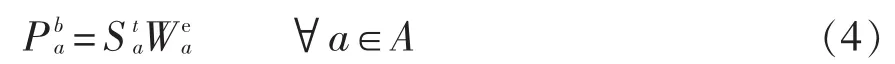
式中：a为车辆类型；A为车辆类型集合；A={Pr,Ta,Bu}，分别对应表示私家车、出租车和公交车；为a类电动汽车中第b辆电动汽车日电量需求；为a类电动汽车日均行驶距离；为a类电动汽车百公里耗电量。

（2）各类型电动汽车总换电需求为

（3）电动汽车一天总换电需求为

式中，L为电动汽车总换电需求。

2.3 规划区内路网节点换电需求

电动汽车换电站的服务范围取决于用户的换电需求，而换电需求与各路段的车流量密切相关，由于规划区内路段数比路网节点数多，为了降低计算维度，将规划区域内各路段的交通流量用路网节点交通流量表示[10]。根据道路网中车流量的大小，对电动汽车换电站换电需求按比例进行分配，将换电站换电需求分配在路网节点处，得到路网节点换电需求分布，即

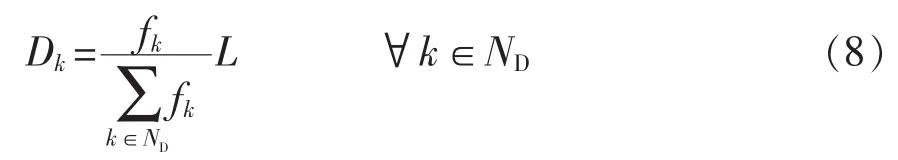
式中：k为换电需求点；ND为换电需求点集合；Dk为k点的换电需求大小；fk为路段车流量。

2.4 集中充电站数量预估

电动汽车集中充电站占地面积大，投资费用高，单个集中充电站可服务多个换电站，以拟建换电站的数量范围来确定拟建充电站的数量范围，即

式中：Mmin和Mmax分别为拟建充电站最小数量和最大数量；N为拟建换电站个数；Smax和Smin为单个充电站服务的最大换电站个数和最小换电站个数。

3 充、换电站联合规划模型

3.1 目标函数

电动汽车充、换电站联合规划模型综合考虑换电站建设运维成本、用户损耗成本、换电站建设运维成本和电池配送成本，以年综合成本总和最小为目标函数，即

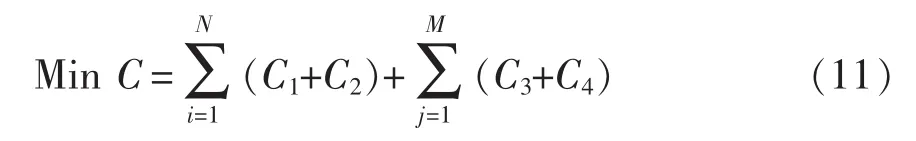
式中：C为年均综合成本；C1为换电站建设运维成本；C2为用户损耗成本；C3为充电站建设运维成本；C4为电池配送成本。

（1）换电站建设运维成本为

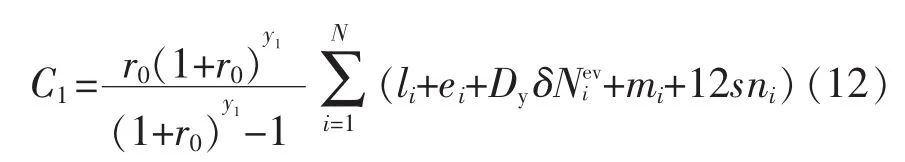
式中：i为换电站候选站址；r0为贴现率；y1为换电站的运行年限；li为换电站i的基建费用；ei为换电站i换电设备总投资费用；Dy为一年内各类型电动汽车换电池的次数；δ为每次换电的平均换电成本；为换电站i服务范围内所有类型的车辆数量；mi为换电站i的维护费用；ni为换电站i工作人员数量；s为工作人员平均每月工资。

（2）用户损耗成本。用户驾车行驶至换电站会消耗需要一定电量，且抵达换电站准备换电时可能会发生排队情况，所以用户损耗成本包括行驶至换电站过程中消耗的电量成本和换电站内等待的时间成本，即

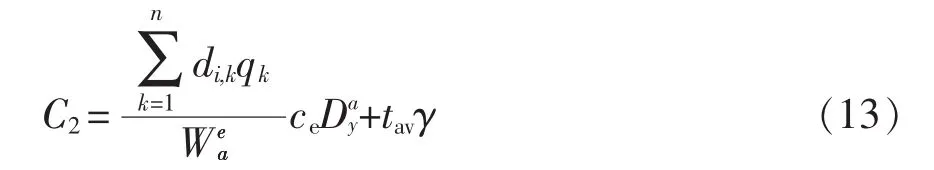
式中：n为换电站i服务区域内包含的换电需求点个数；di,k为需求点k到换电站i的距离；qk为换电需求点k需要换电池的用户数量；为a类电动汽车百公里耗电量；ce为单位耗电量的成本；tav为用户在换电站平均等待时间；γ为用户时间成本。

（3）充电站建设运维成本为

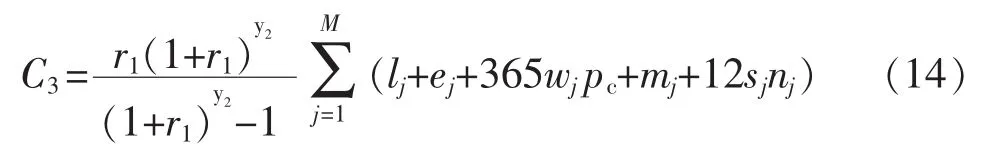
式中：y2为充电站的运行年限；lj为充电站j的基建费用;ej为充电站j充电设备总投资费用；wj为充电站j平均每天用电量；pc为电价；mj为充电站j的维护费用；nj为充电站j工作人员数量。

（4）电池配送成本为

式中：z为运送电池车辆的数量；sc为车辆购置费用；tc为运输电池途中产生的费用；mc为车辆维护费用。

3.2 约束条件

（1）充电站的服务能力约束为

（3）换电站位置距离约束为

式中：dm-n为换电站m与n间隔距离；dmin为两个换电站之间所允许的最小距离。

3.3 模型求解

3.3.1 加权Voronoi图

伏罗诺伊图又称泰森多边形,其可看作由生长点集p中的每个顶点作为生长点以相同的速度向四周扩张，直到在平面上相遇为止而形成的图形，所以除在边缘的顶点形成的是开放区域外，其他的顶点形成的都是凸多边形。由于其所具有的最邻近特性和空圆特性，已广泛应用于地理空间设施选址分析方面。

假设 p=（p1,p2,…,pn），3≤n＜∞ 是欧几里德平面上的一个点集，则任意点的常规Voronoi图定义为

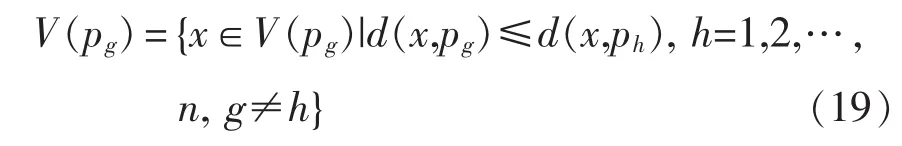
加权Voronoi图是常规Voronoi图的一种扩展形式[11]，定义为

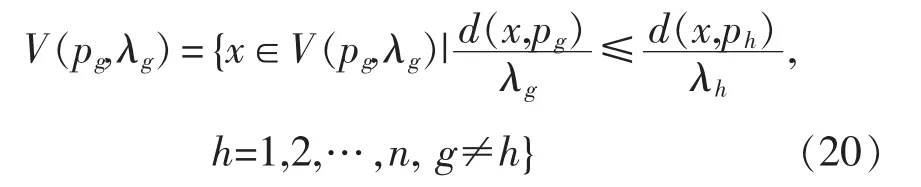
式中：λg（g=1,2,…，n）为给定的 n 个正实数；d（x,pg）和 d（x,ph）为点x与pg和 ph的欧几里德距离；λg为pg的权重，pg≠ph，g≠h，g，h∈{1,2,…，n}；x 为平面上的任意点。当 λ1=λ2=…=λn时，式（20）等价于式（19），即常规Voronoi图是加权Voronoi图权重相等时的特例。

3.3.2 自适应粒子群算法

粒子群优化算法是通过对鸟群捕食行为的研究而形成的一种基于群体协作的随机搜索算法，初始化的群体在搜索空间并行搜索，通过个体间的行为交互达到全局寻优的目的。本文通过对惯性权重ω和学习因子c1、c2进行修改，使PSO算法在陷入局部最优时，能够以更大概率跳出局部最优位置，提高全局寻优的能力。

对惯性权重的选取采用混沌惯性权重粒子群优化算法中的惯性权重更新方法，其迭代公式[12]为

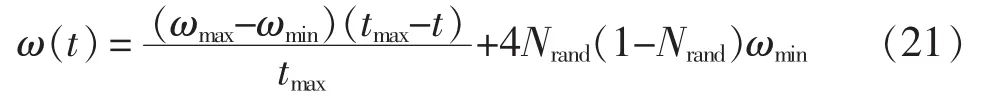
式中：ωmax和ωmin分别为惯性权重ω在开始和结束迭代时的取值；t为当前迭代的次数；tmax为最大迭代次数；Nrand为[0,1]间的随机数。

学习因子c1和c2采用非线性反余弦加速，c1先大后小，c2先小后大，构造方式[13]为

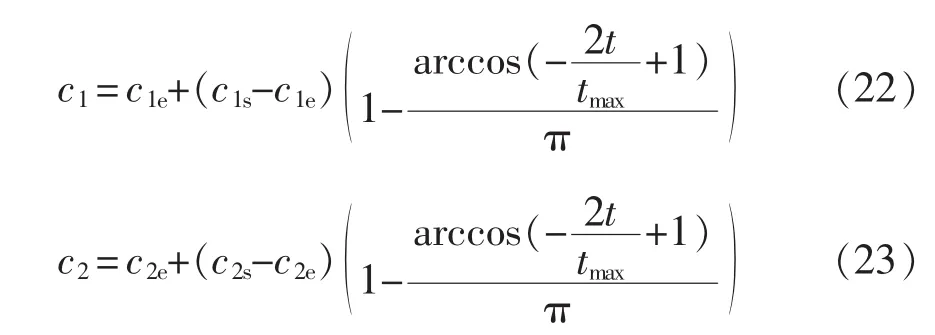
式中：c1s和c2s为迭代初值；c1e和c2e为迭代终值。本文中，c1s、c1e和 c2s、c2e分别取为 2.5、0.5 和 0.5、2.5。

3.3.3 加权Voronoi图与自适应粒子群算法联合求解流程

虽然Voronoi图在地理设施选址方面具有一定优势，但所得到的结果容易陷入局部最优，本文采用改进后的自适应粒子群算法与加权Voronoi图联合求解。具体规划步骤如下。

步骤1由第2.1节和第2.2节方法分别计算出规划地区目标年电动汽车保有量和电动汽车换电需求，结合不同等级换电站的服务能力，确定换电站的总数量范围[Nmin,Nmax]，以换电站数量N为循环变量，寻找不同数量换电站的最优解。

步骤2站址初始化。初始化粒子的位置和速度，将随机生成的N个换电站站址坐标编译为粒子群初始位置X。根据换电站站址坐标集作加权Voronoi图，Voronoi图的凸多边形对应各换电站的服务范围。

步骤3粒子适应值计算。根据式（12）和式（13）计算出换电站建设运维成本和用户损耗成本之和。

步骤4更新粒子的速度和位置，并且编译为新的换电站站址坐标集。

步骤5判断是否达到收敛条件。若达到，则输出结果；若未达到，则返回步骤2进行循环,直至达到最大迭代次数。

步骤6根据换电站的规划结果，确定充电站的总数量范围[Mmin,Mmax]，以充电站数量M为循环变量，寻找不同数量充电站的最优解。

步骤7重复步骤2～步骤5，对充电站进行规划。同时，以充电站数量M作为循环变量，根据生成的M个充电站站址坐标作充电站的加权Voronoi图，根据式（14）和式（15）计算得到充电站建设运维成本和电池配送成本之和，满足收敛条件后输出结果。

4 算例分析

4.1 算例概况

以2025年某市电动汽车充、换电站规划为例，规划区域参照文献[14-15]并加以适当修改，区域路网结构如图2所示。为简化计算，电动私家车和出租车型号统一选取帝豪EV300，电动公交车型号为比亚迪K9。根据北京市出台的《电动汽车电能供给与保障技术规范》指导文件[16]，结合当前国内已建成的充、换电站概况以及电动汽车发展趋势，对规划区域目标年的充、换电站等级进行合理假定，相应数据如表2所示，充、换电站规划模型相关参数如表3所示。

4.2 电动汽车保有量预测

以2015年为基准年，预测2025年电动汽车保有量。设该区域2015年的私家车、出租车和公交车保有量分别为118 507、49 375、26 019辆，传统汽车Bass模型参数中创新系数P为0.003，模仿系数Q为0.209[17]。以传统汽车市场为比较对象，基数定为1，对各类型电动汽车内、外部影响因素进行评分，评分结果见表4。再根据式（2），求得电动汽车Bass模型的P、Q参数，如表5所示。

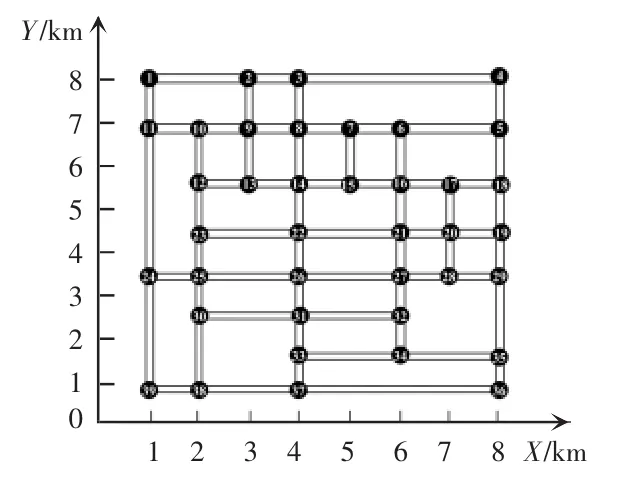
图2 规划区域路网结构示意Fig.2 Structural diagram of road network in the planning area

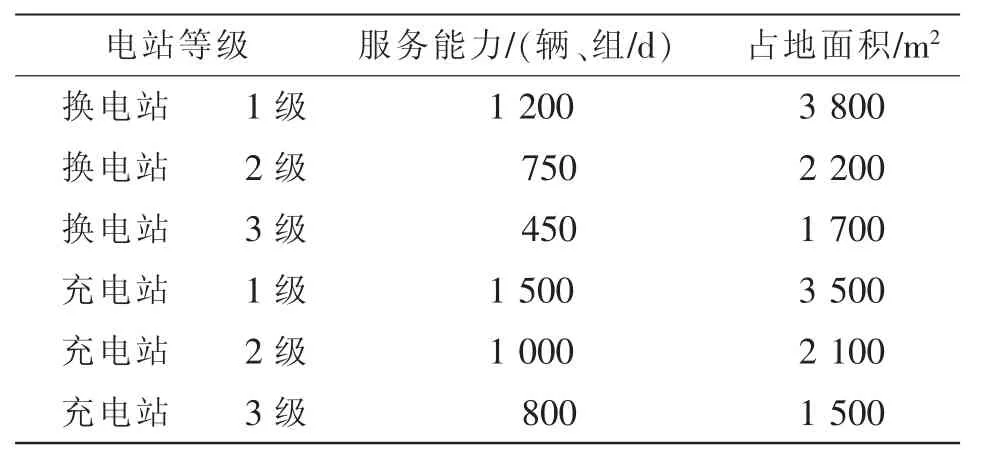
表2 充、换电站基本参数Tab.2 Basic parameters of charging and battery swapping stations

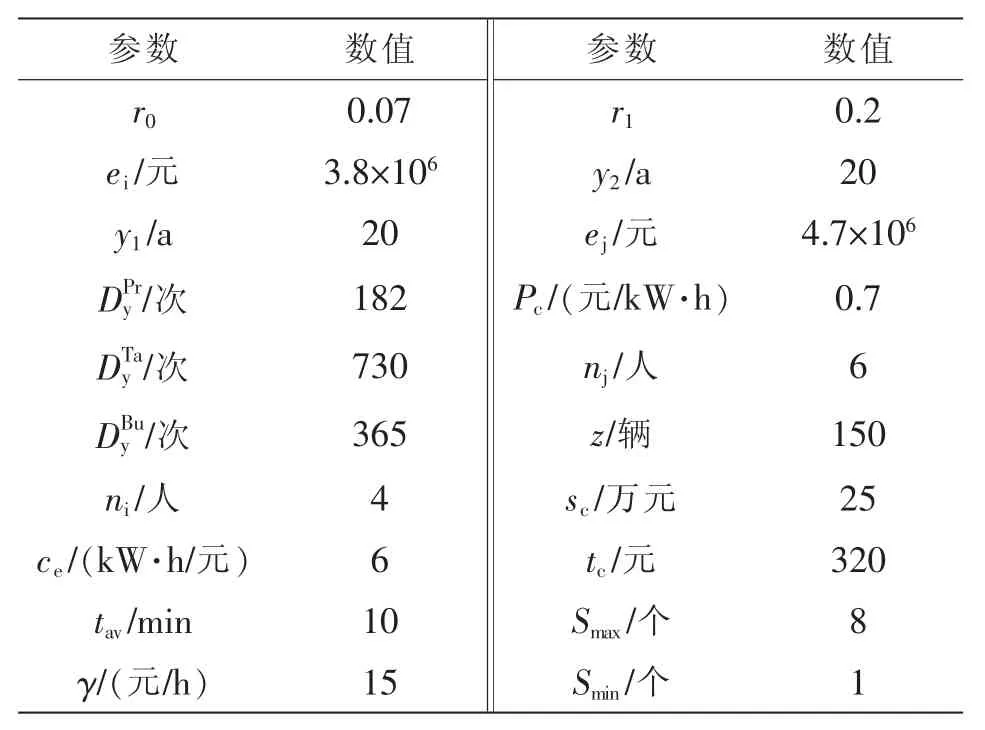
表3 充、换电站规划模型参数Tab.3 Parameters in the planning model of charging and battery swapping stations

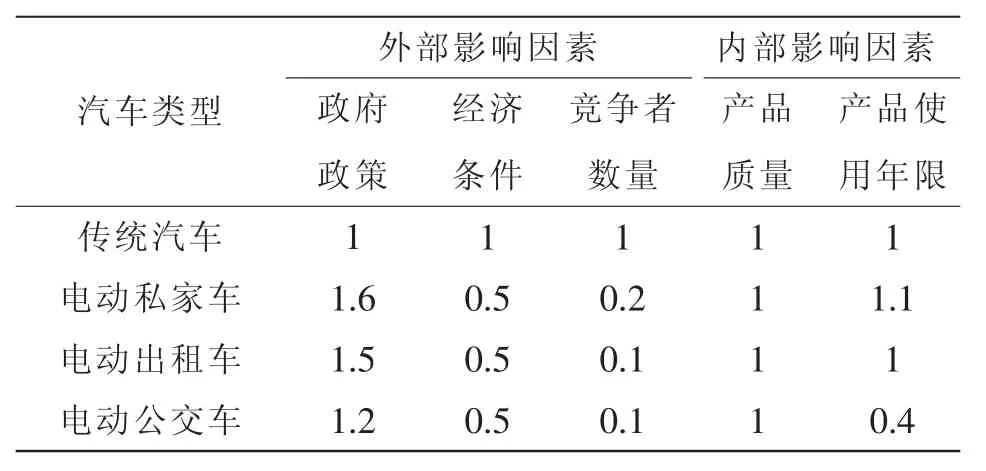
表4 电动汽车与传统汽车影响因素比较Tab.4 Comparison of influencing factors between EVs and conventional cars

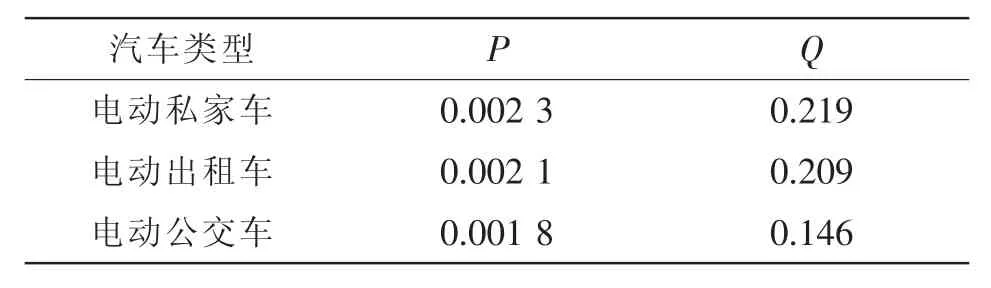
表5 电动汽车Bass模型参数Tab.5 Parameters in Bass model of EVs

根据表5所求结果，由式（1）和式（3）得出电动汽车保有量预测值，至2025年，电动私家车、出租车和公交车数量分别为53 106、10 427和7 702辆。

4.3 电动汽车换电需求预测

帝豪EV300百公里耗电量为13.7 kW·h/100 km，电池容量为41 kW·h，比亚迪K9百公里耗电量为125 kW·h/100 km，电池容量为600 kW·h。私家车主要作为日常通勤使用，设平均每天行驶距离为45 km，出租车行驶路线随机，通常采用两班倒形式，设平均每天行驶距离为380 km，公交车行驶路线固定，且一天运营时间较长，设平均每天行驶距离为290 km，根据第2.2节模型求出3类车一天总换电需求，再将总换电需求分配至路网节点，区域路网各节点典型日车流量参照文献[14],由式（8）求得路网各节点换电需求，如表6所示。

4.4 规划结果

由第3.3节求解流程对换电站进行规划，设置粒子种群数为100，迭代次数为150，惯性权重ωmin与ωmax分别取0.4和0.9。根据换电站等级与路网各节点换电需求，得到规划区拟建换电站数量范围为6～12座，各项成本随换电站数量的增加变化趋势如图3所示，不同换电站数量下年综合成本如表7所示。

由图3和表7可以看出，随着拟建换电站数量的增加，用户消耗成本和建设运维成本变化趋势不同。其中，用户消耗成本呈下降趋势，主要由于当换电站数量增加，其服务范围逐渐减小，用户行驶至换电站与在站内等待的成本会减少；而建设运维成本呈上升趋势，主要是因为换电站基建费用、设备投资较高，导致建设运维费用增长较快，且其增长趋势大于用户消耗成本下降趋势，使换电站规划总费用先降后增，当拟建换电站数量为10时，总费用最小为3 650.71万元。换电站位置及服务范围如图4所示，换电站最优规划方案如表8所示。

根据换电站规划结果，由2.4节模型计算得到充电站数量范围为1～5座，按照第3.3节求解流程继续对充电站进行规划，算法参数选取与前面一致，各项费用随充电站数量的增加变化趋势如图5所示，不同充电站数量下年综合成本如表9所示。

由图5和表9可以看出，随着拟建充电站数量增加，电池配送成本逐渐减少，且充电站数量由1至3时下降较快；而建设运维成本逐渐增加，且增长趋势大于电池配送成本减少趋势；充电站规划总费用先降后增，当拟建充电站数量为3时总费用最小，为2 591.56万。各充电站位置及服务范围如图6所示，充电站最优规划方案如表10所示。

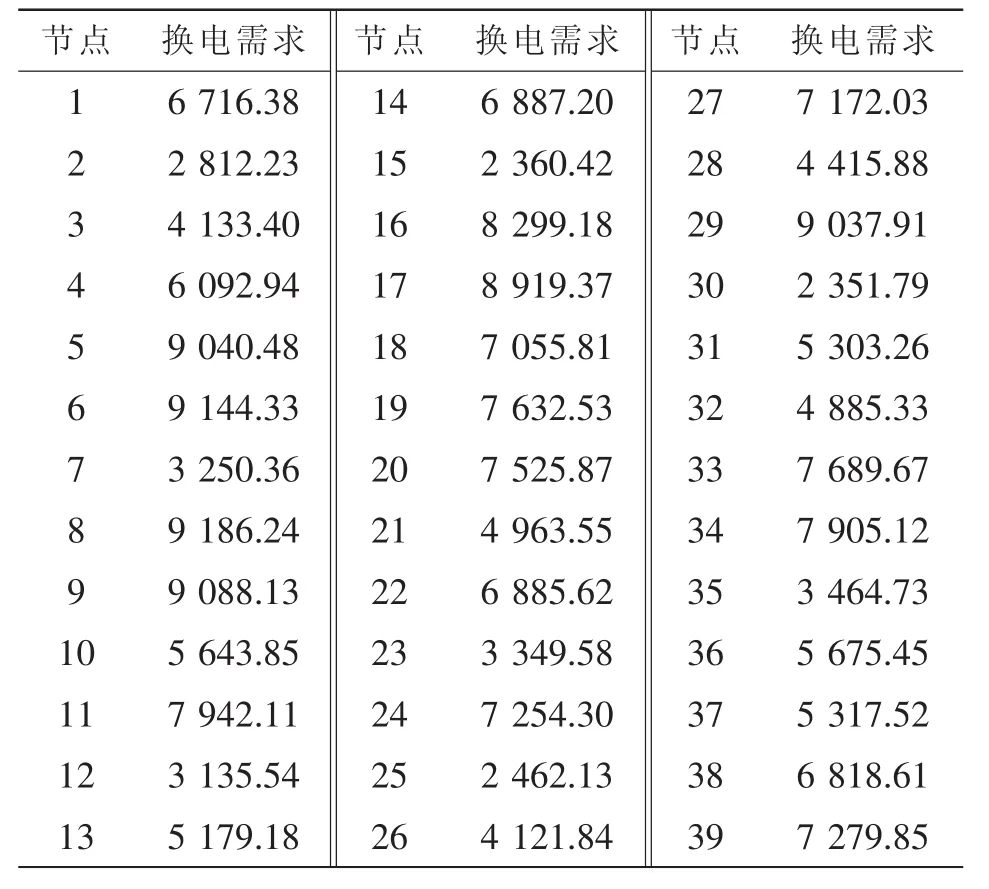
表6 各路网节点换电需求Tab.6 Battery swapping demand at each node in the network kW·h

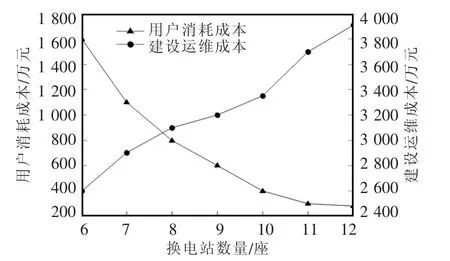
图3 各项成本随换电站数量变化趋势Fig.3 Changing trend of various costs with the number of battery swapping stations

表7 不同数量换电站的年综合成本Tab.7 Annual comprehensive costs when the numbers of battery swapping stations are different

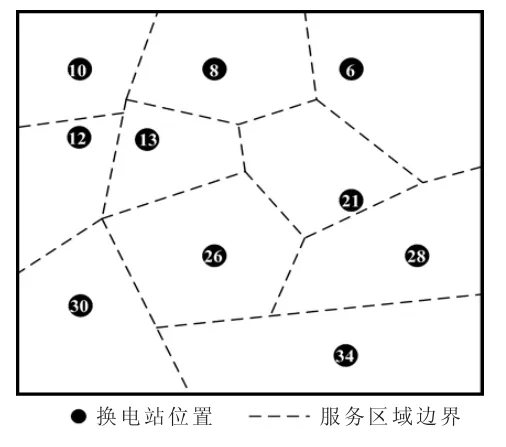
图4 换电站位置与服务范围Fig.4 Positions and service ranges of battery swapping stations

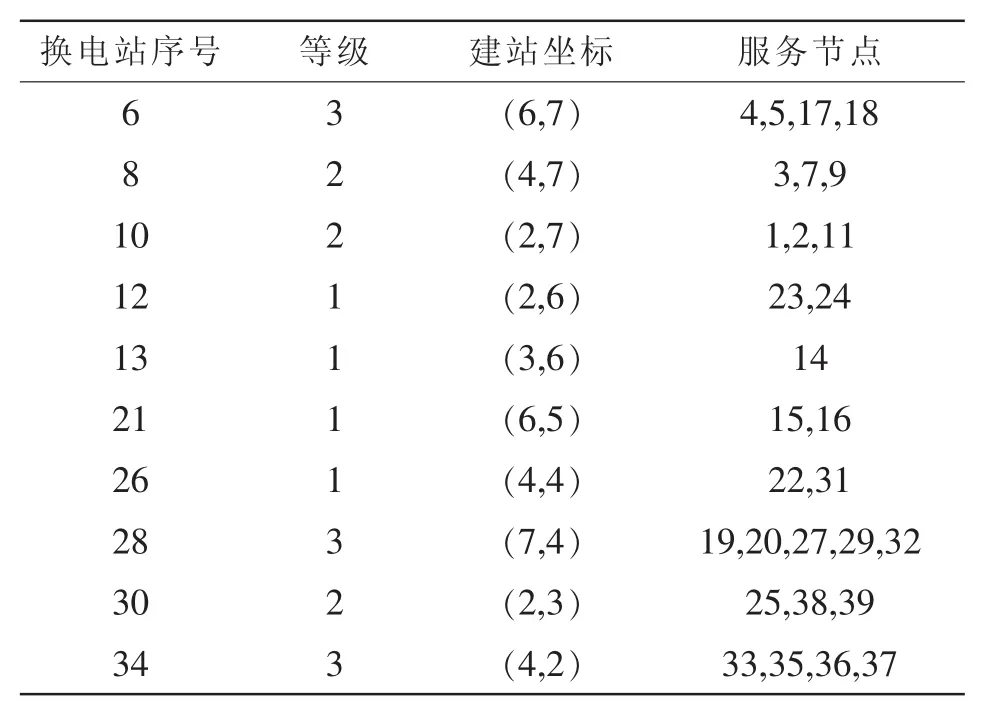
表8 换电站最优规划方案Tab.8 Optimal planning scheme of battery swapping stations

表9 不同数量充电站的年综合成本Tab.9 Annual comprehensive costswhen the numbers of charging stations are different

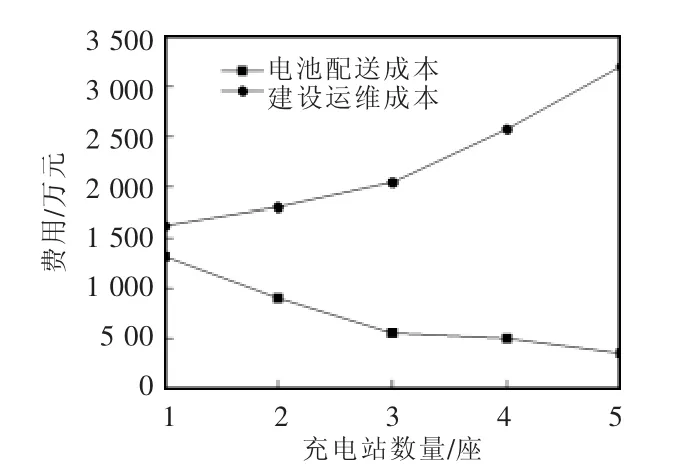
图5 各项成本随充电站数量变化趋势Fig.5 Changing trend of various costs with the number of charging stations

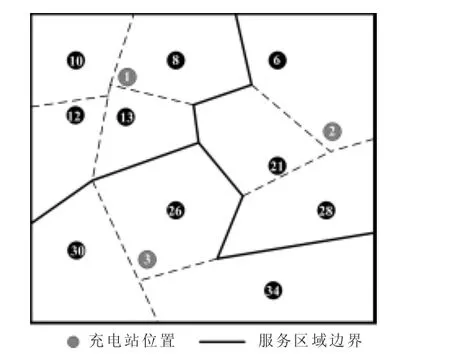
图6 充电站位置与服务范围Fig.6 Positions and service ranges of charging stations

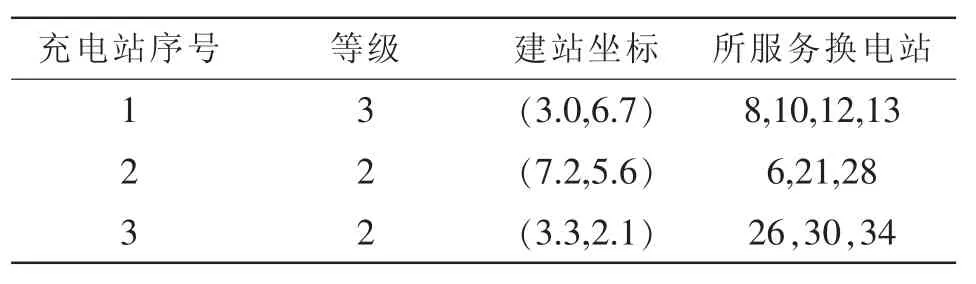
表10 充电站最优规划方案Tab.10 Optimal planning scheme of charging stations

5 结语

针对电动汽车电能补给设施规划问题，在“集中充电，统一配送”的背景下，本文提出一种电动汽车充、换电站联合规划方法，以充、换电站建设运维成本、用户损耗成本和电池配送成本之和最小为目标，以满足充、换电站服务能力，换电站位置距离为约束，建立了充、换电站联合规划模型，算例分析表明，粒子群算法的引入有效避免了单独采用Voronoi图来确定站址时的不足，使得到的的充、换电站位置以及服务范围更加合理，且换电站的规划结果会对充电站的规划产生一定的影响；经济性方面，对规划方案以年均综合成本最小进行优选，同时兼顾了电动汽车用户和充、换电站运营商的利益。