基于实时路况信息的灾后应急配送路径选择系统
黄辉,吴翰,杨佳祺,未珂
(西北工业大学 管理学院,西安 710129)
中国是一个自然灾害多发的国家,汶川地震、雅安地震等重大灾害给国民带来了严重的物质和精神方面的损害。自20世纪,我国发生数次重大灾害,包括1979 年唐山大地震,2008 年汶川地震,2010年舟曲泥石流等。高强度的灾害往往伴随着毁灭性的损失,应急救援成为灾害发生后立即启动的最重要也是主要的工作。对应急事件的救援是一个系统工程,由于重大灾害往往伴随着次生灾害的问题,持续影响救援工作的开展,如余震可能会使道路损坏,降水量影响道路通行能力等。救援物资在整个灾后救援中有着举足轻重的地位。灾后,需要面对随时会发生的次生情境,合理安排应急物流路线,在救援进行中随时改进路线以适应不断变化的道路状态,提高救援效率,控制救援风险。
对于应急状况下救援路线规划的问题,国内外学者做了相关研究。Zhang等[1]提出了一种仿生算法,以求解救援过程中行驶速度变化情况下的应急路线规划问题。刘春年等[2]提出了基于路阻函数理论与Dijkstra算法的最优路径数学模型。代颖等[3]构建了应急物资配送中心定位和配送路径安排的联合决策问题的定位-路径问题模型。袁媛等[4]建立了最小化灾害疏散时间和最小化疏散路线复杂度的应急疏散路径选择双目标优化模型。Rath等[5]研究了灾后应急物资运输中的定位-路径问题,模型中考虑了短期和中期的救援经济性的多目标优化模型,并考虑了人道主义因素。魏航等[6]研究了时变随机网络下有应急限制期的应急路径选择问题,通过定义应急路径的风险和成功,给出算法,得出应急限制期下的有效应急路径。刘杨等[7]提出了城市应急车辆出行前救援路径选择的多目标规划模型。范文璟等[8]针对时变网络环境下应急路径问题,提出了考虑跨越多个时段的行驶问题的城市路段行驶时间的计算方法。谢红薇等[9]提出了结合遗传算法和模拟退火算法,提出了一种求解应急最优路径的方法。应急救援有着弱经济性,但有些研究会还将救援成本作为优化的目标之一。Tzeng 等[10]考虑救援时间成本最小化,以及救援满意度最大化,构建多目标应急路径优化方案。很多研究从不同的角度来考虑时变应急路径选择的问题,但难以全方位地实现实时根据数据输入确定救援路线,并根据仿真数据,从宏观角度随时规划救援路线。本文根据自然科学学科专家的评估,得到特定状况下最优路线改变的概率,让整个救援路线选择体系从实时数据的输入可以即刻得到最优的当前路线,亦可利用仿真数据,配合GIS实现整个救援过程的实时优化与规划,以指导决策的制定。尽管国内外学者对时变应急物流路径选择做过不少研究,但考虑应急状态下道路综合属性实时变化,并运用仿真程序模拟路线选择过程的研究仍较少。
为此,本文提出适用于灾害后次生灾害等情况随时发生状态下应急救援路径选择的方法。通过检测道路状态,根据不同的道路受次生事件影响及其程度,随时调整救援最优路线,结合地质等学科,组成一套应急路径选择体系。该体系不仅支持根据实际情况改变救援的行进路线,还可用来进行多次仿真,模拟救援情况,仿真结果可供决策者规划整体救援资源的分配。最后,通过算例进行说明。
1 问题描述
灾害发生后,会出现各种次生事件,如余震、道路阻塞、强降水等。次生事件的发生会导致应急路网状态的改变,如余震破坏道路使道路无法通行、降水使道路通行能力下降等。次生事件的发生随时可能会使路网状态发生变化,进而使应急救援最优路线发生改变。因此,在灾后应急配送过程中,为达到最快送达的目的,应急配送路径的选择通常不仅需考虑路线长度,还需综合考虑道路通行能力、路段发生二次灾害等因素。根据对道路状态的实时监测,将道路状态量化,动态实时调整救援路线,实现应急物资最快送达的目的。
2 建 模
2.1 综合多种实时路况状态因素的道路状态量化
道路的情境状态,可以由各个路段的多种道路属性指标来描述。自然灾害发生后,根据该灾害本身的性质,属性指标的选取应当呈现多样化。为实现应急物资最快送达,本文只考虑4种主要道路属性来描述一个路段的状态特征:①路段区域二次灾害发生风险程度f1。②路段区域降水状况f2。③路段拥堵程度f3。④路段υiυj长度Lυiυj。
灾害发生后,救援人员需要考虑的道路属性不限于上述4种属性,本文暂且以这4种属性来描述路径选择过程。
文中符号含义:
υi—— 结点i,i=1,2,…,10
υiυj—— 从i点到j点的路段
P(υi)—— 最短路算法中,υi为P标号点
T(υi)—— 最短路算法中,υi为T标号点
fi—— 路段属性i
t1——含有路段υ1υj的路网中的最短到达时间
t2—— 不含路段υiυj的路网中的最短到达时间
tυiυj—— 路段υiυj期望通行时间
tυiυjc—— 路段υiυj的临界值
Lυiυj—— 路段υiυj的路程长度
V0υiυj—— 理 想 状 况 下 路 段υiυj的 平 均 通 行速度
Vυiυj——路段υiυj在路段属性影响下的实际平均通行速度
—— 路段υiυj的道路属性fn的评估值,取值范围[0,1]
Pυiυj—— 路段υiυj的稳定概率
路段长度直接影响整体运输时间。其他3种属性均以一定的程度影响车辆通行的平均速度。
在多种属性影响程度量化上,各相关学科专家对各路段实时监控数据,给出属性fn对路段通行平均速度影响程度的评估值,其中为属性fn对路段υiυj的影响程度,且∈[0,1]。当=0时,路段的fn属性处于极端情况最差值,即该属性此时的状态使道路中断;当=1时,表示属性fn处于理想状态最优值,即该属性不影响路段的通行速度。
设道路υiυj在各种属性均处于理想状态下的平均速度为V0υiυj,假设路段除其路程属性外共有k种属性,根据下式可得综合k种属性后的路段通行平均速度,即
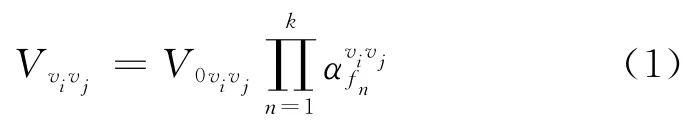
路段长度除以该路段通行平均速度Vυiυj,进而计算出路段υiυj经过综合考虑各种道路属性调整后的该路段期望通行时间为
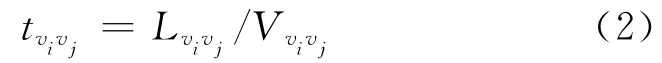
2.2 基于改进Dijkstra算法的应急配送路径实时选择
Dijkstra算法是解决网络图中最短路径问题的经典算法。本文将路段期望通行时间tυiυj作为Dijkstra算法中的路径长度属性,将时间作为路网中各弧的弧长。根据改进的Dijkstra最短路算法,可计算得到到达受灾点最短时间的网络路径,即最优路线,从而达到使救援车辆最快到达受灾点的目的。
如图1所示,灾害发生后,由相关学科如地质、气象、水文等工作者及实时监控人员对路网中各条道路的各种属性进行评估后得到数据作为输入,确定路网中各路段的期望通行时间,并得到该路网状态下的最优路线。救援队伍可即刻按照该初始最优路线出发。由于路段属性状态的实时变化,某路段可能发生某些次生事件,影响了路段的通行能力,进而影响路段的期望通行时间,可能会导致最优路线变化。

图1 灾后实时应急路径选择示意图
在救援队伍行进过程中,应实时监测路网状态,若最优路线发生改变,应用如下方法寻找新的最优路径。改进的Dijkstra算法:
(1)初始j=0;令Sυ1=1,P(υi)=0,u=υ1,对于不为υ1的每个点υi,令T(υi)=tυ1υi,若点υ1与υi可以直接连接,则令P(υi)=1,Sυi=0。
(2)若Sυn=1,可知T(υn)是由υ1到υn的最短路线,则可得出最短路,计算终止;否则,转(3)。
(3)找出到起始点时间最短的点,令T(υi)=min{T(υi)},此时,Sυ1=1,u=υ1,Su=1。
(4)如果点υi是某条弧的终点,在这个终点上发生了参数的改变,且参数改变是在救援车辆从该点相邻的上一点向该点出发之后发生的,则设定点υi为新的起始点。根据改变后的道路参数,使用基本最短路算法计算出新的最短路;否则,转(5)。
(5)更新所有T(υ1),Sυ1=1。令
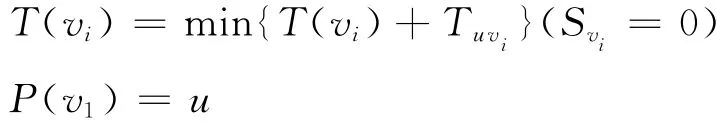
j自增1,转(2)。
结合相关学科研究成果,求得路网所需期望通行时间最短的路线。利用计算机仿真获得仿真数据供决策者分析,以提前规划路线,指导应急救援运输任务。尽可能地充分利用时间以及道路资源等应急救援资源,提高救援效率。
2.3 路段临界值与稳定概率
如图2所示,若当救援车辆到达路网中某点时,道路状态发生变化,根据上述方法会立即生成最新的最优路线。结合计算机技术,形成路网状态信息系统,随时根据新输入的道路状态数据计算出最新的最优路线。该方法可以在路网情况发生改变之后找出当时的最优路线,但若能提前计算出最优路径发生变更的临界点,面对不确定的事件发生,更能支持决策者做出恰当的路线选择决策。
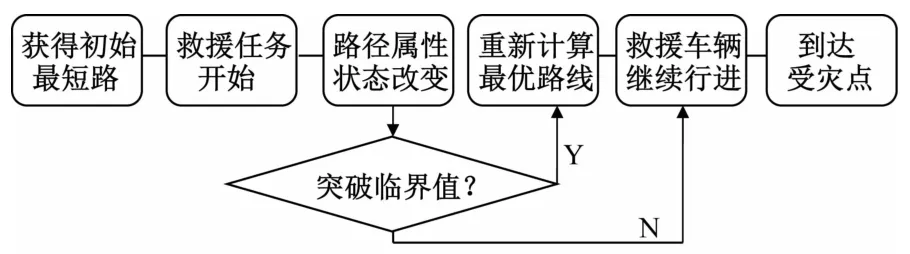
图2 应急路径实时选择流程
该方法不考虑车辆正在行进的路段发生次生事件的情况,若一辆车所正在行驶的路段发生参数变化后,只可能有如下两种情况发生:①此路不通(如巨石挡路),车辆掉头回到前一个结点,换路行进。相当于重新选择路线。②车辆已经走过发生阻挡车辆行进的事件的点,不影响车辆行进,车辆继续前行,如在车辆后方100 m 处发生巨石坠路事件,而车辆向前行进并不受影响。因此,本研究不考虑此类情况。
若因当前最优路线中的某路段υiυj的期望通行时间tυiυj改变而导致最优路线改变时,计算机可以帮助计算出新的最优路线,而tυiυj改变到何种程度才会令最优路线发生改变,就是临界值为何值,记作tυiυjc。即假设其他路段状态不变,υiυj发生了次生事件,导致tυiυj>tυiυjc,进而导致最优路线的改变;而当该次生事件并未导致tυiυj>tυiυjc,则不会改变最优路线,tυiυjc即为路段υiυj的临界值。根据上述对临界值tυiυjc的定义,在实时变化的路网中,可得:①临界值tυiυjc是对于已经被选作最优路线中的路段而言的,而不在最优路线上的路段本身并没有临界值;②随 着路网状态的改变,特定路段tυiυj的临界值tυiυjc也会发生变化。
临界值的计算方法:在某一路网状态下,首先在路网中寻找到最优路线,即总期望通行时间最短的路线,并计算出该总期望通行时间t1。对于最优路线上的某路段υ1υj,将υiυj路段从原路网中剔除,再在剔除路段υiυj的新的路网中找出最优路线,并计算该最优路线的总期望通行时间t2。则对于初始状态的最优路线,在其他条件不变的状况下,当tυiυj变化到一定程度,使t1>t2时,会使路网最优路线发生改变,即υiυj的时间临值为
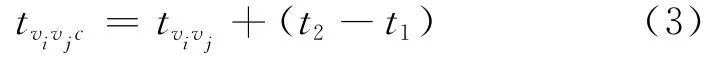
当路段υiυj在最优路线上时,其总会存在临界值tυiυjc,tυiυjc也会因道路属性的改变而改变,故在该路径选择系统中,当道路属性状态发生任何变化,需立即计算新的tυiυjc。另外,若想要提前仿真模拟车辆到达受灾点的过程,则需要结合其他学科,计算各种次生事件发生的概率,提前知晓众多救援路线各自最终被使用的可能性。
根据相关学科的研究成果,张彭等[12]提出一种拥堵概率估计方法,并给出了概率分布估计。张国平[13]对灾区滑坡及雨量进行了分析,亦给出概率模型。根据相关研究,在应急事件发生后,应急路网中各路段所对应的多种救援路径属性,如路段区域余震风险程度f1,路段区域降雨状况f2,路段拥堵程度f3各自概率分布情况。综合特定路段的所有属性的概率分布情况,可得路段综合属性的概率分布。本研究中,路段的综合属性以期望通行时间tυiυj来描述。对于最优路线上每个路段υiυj,均有各自的临界值tυiυjc,在 其 期 望 通 行 时 间tυiυj的 分 布 中,可 得tυiυj<tυiυjc的概率,本文称为稳定概率Pυiυj。
综上所述,应急救援路径确定方法如下:救援任务下达后,根据气象、地质等相关监测,输入从出发点到受灾点之间的路网的各个路段属性状态值,以及各个路段的稳定概率Pυiυj。通过属性值求得初始状态下各个路段的期望通行时间tυiυj,并在以各条路段的tυiυj为弧长的路网中运用算法求得最短路,即初始最优路线。重复仿真试验,得到各路线最终的行驶概率。救援队伍沿着该初始最优路线出发。出发后,面临着不确定的次生事件,当次生事件发生,应立即根据实时监测输入最新的道路属性值,计算出实时tυiυj、tυiυjc、Pυiυj。形成新的路网参数,用最短路算法重新计算最优路线。每当次生事件发生,均应立即重复仿真试验(最短路算法时间复杂度O(nlbn),以目前计算机计算能力,规模在30个结点的路网,万次仿真时间在3 min以内,满足实时性要求),得出路网的每条可能路线为最终行驶路线的可能性,供决策者参考,根据每条线路的风险程度与所需时间和每种救灾物资的重要程度及需求紧急程度,分配给载有不同物资的车辆。根据新的最优路线规划继续行进,以此循环,直到车辆到达受灾点。并运用高性能计算机,实现实时多次仿真,获得数据以支持决策。
3 算 例
重庆υ1为应急物资供应点,雅安υ10为受灾点,即物资需求点,υ1~υ10之间的路网如图3所示。
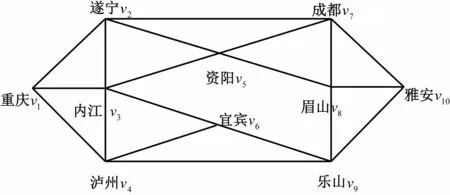
图3 抽象路网
为便于算例说明及仿真分析,做出如下假设:
(1)所有线路均可双向行驶。
(2)路线一旦改变,可立即通知所有车辆的救援人员。
(3)路网中每个路段理想平均速度均为V0υiυj=80 km/h。
(4)为模拟应急状态下路网,假设路段的稳定概率随机变化。
表2所示为道路属性输入值。
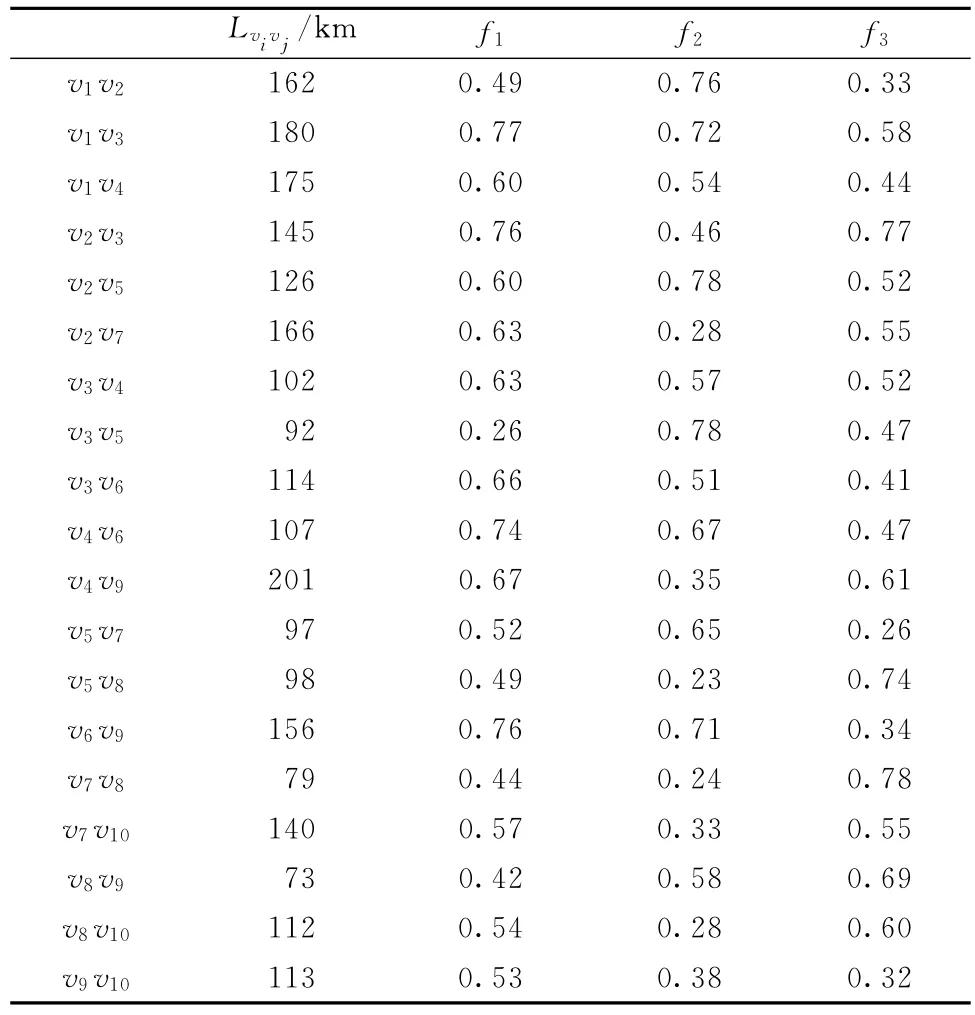
表2 道路属性输入值
根据式(2),计算各路段的初始的期望通行时间,如表3所示。
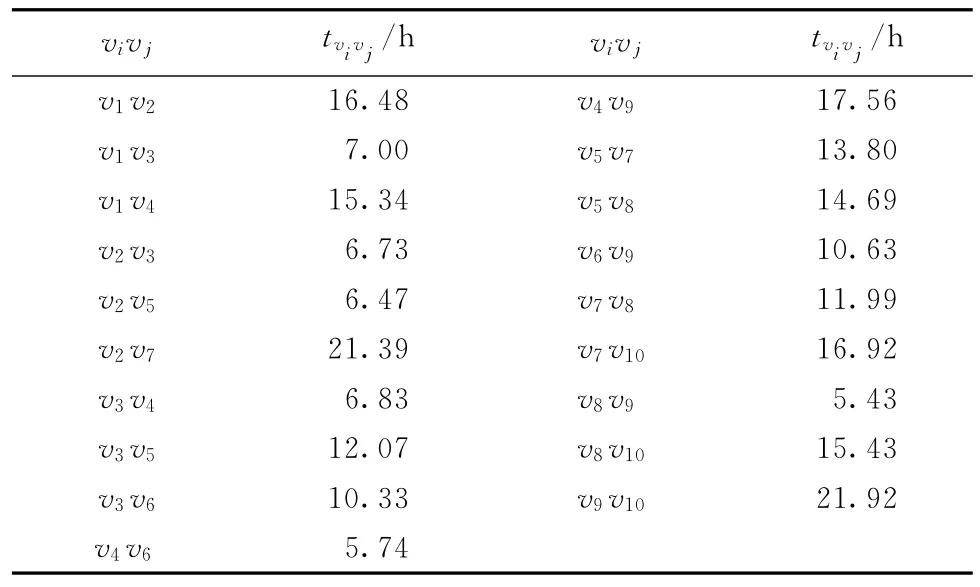
表3 路段初始期望通行时间
根据上述数据,应用Dijkstra算法得出初始最优解为υ1-υ3-υ6-υ9-υ8-υ10。
因临界值tυiυjc在救援过程中是随着路况而不断变化的,在此仅给出救援队伍出发后第1个路段υ1υ3时的临界值tυiυjc,即对应该初始最优解,计算临界值。根据式(3),计算数据如表4所示。
实际救援过程中相关气象、地质等监测人员,根据上述临界值,通过综合相关学科对次生事件发生的可能性的预测,得出各路段的稳定概率。本算例中,假设在初始状态下,每路段υiυj平均通行时间不突破临界值tυiυjc的概率(稳定概率)如(随机取得)表5所示。

表4 初始临界值(对于初始最优路线为v1-v3-v6-v9-v8-v10)
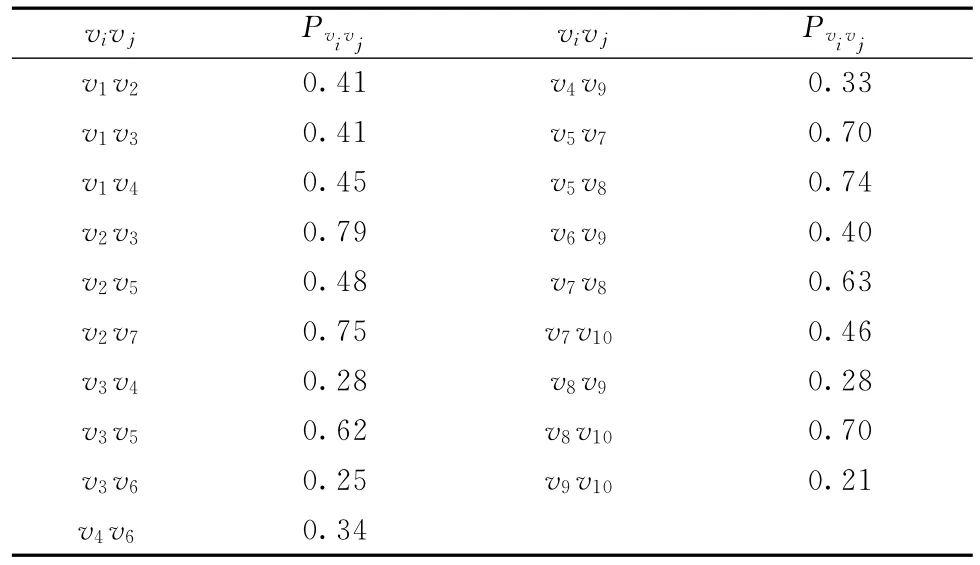
表5 路段初始稳定概率
实际救援中,随着救援的推进,路段稳定概率会发生变化。利用地质、水文、交通等相关学科,通过监测每次属性值的变化,随时计算出当前状态下稳定概率。由于导致概率变化的因素较多,且需相关学科的支持,本文仿真假设路段的稳定概率随机变化,反映到仿真程序中,车辆每从一个结点出发走向下一个结点,取一次随机数,作为各路段的稳定概率,由此模拟救援过程中稳定概率的变化情况。
根据初始最优解,救援车辆从点1出发,沿初始最优解为υ1-υ3-υ6-υ9-υ8-υ10,行进在路段υ1υ3上时,会面临υ3υ6、υ6υ9、υ8υ9、υ9υ10这4个路段发生次生事件而改变其tυiυj的可能性,即tυ1υ6可能超过tυ3υ6c、tυ6υ9可能超过tυ6υ9c、tυ8υ9可能超过tυ8υ9c。根据表5,υ3υ6的稳定概率Pυ3υ6=0.41。生成控制概率的随机数,以模拟在一定的概率条件下υ3υ6路段次生事件发生的情形,可能产生如下结果:①若tυ3υ6超过临界值tυ3υ6c,则最优解变为不选择υ3υ6的路段的最优路线:υ3-υ5-υ8-υ10,救援队伍沿该路线行进,并在到达υ5之前监测υ5υ8的属性值,观察其是否突破临界值tυ5υ8c,如此循环直至终点。对于原最优路线上其他路段υ6υ9、υ8υ9、υ8υ10,进行相同的监测,并根据次生事件对道路属性的影响情况,随时调整最优路线。②路段υ3υ6、υ6υ9、υ8υ9、υ8υ10各自的tυiυj均未超过各自的tυiυjc,则到达υ3后,继续沿着原最优路线υ1-υ3-υ6-υ9-υ8-υ10行进,在到达υ6之前继续监测路段υ6υ9、υ8υ9、υ8υ10的属性值变化,判断其是否突破其临界值tυ5υ8c,并判断是否改变路线。在整个救援运输过程中,依次循环、计算当前最优路线,直到救援队伍到达受灾点。
本例运用多次仿真计算各个路线被选择的次数。当一次仿真结束后,保存记录本次仿真的路线结果,在多次仿真中,记录所有结果路线出现的次数,收集并统计,对于路网中每个点,运用配置Intel i3,主频2.26 GHz CPU,2 GB 内存的计算机,在Windows 7操作系统下运用MATLAB R2 012 A编写程序,进行10 000次仿真,因靠近终点的结点到终点的路径较为单一,且无特别的研究意义,仅给出距离终点较远的结点(υ1,υ2,υ3,υ4)的仿真结果:
(1)以重庆(υ1)为起点的仿真结果(程序运行时间40 s)如表6、图4所示。
通过上述数据,可以看出,当车辆沿初始最优路线υ1-υ3-υ6-υ9-υ8-υ10出发后,在最终到达目的地时,可能会出现4种路线状态。路线最终被选择的可能性不尽相同,决策者可以利用该方针数据,规划运输资源的分配。
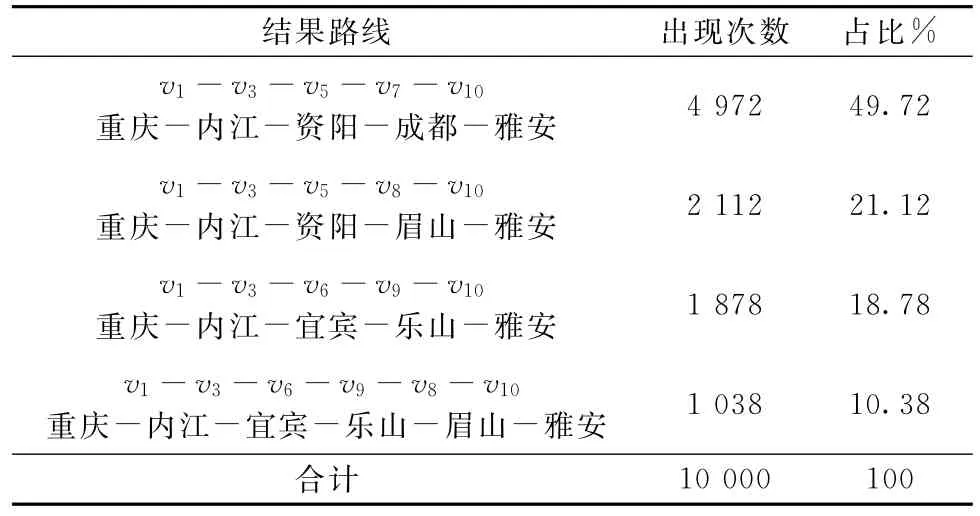
表6 仿真结果统计(重庆(v1)为起点)
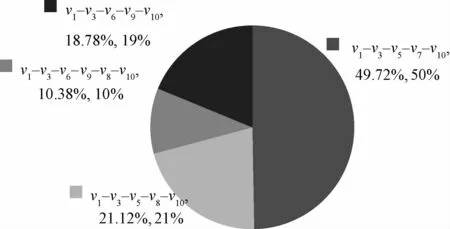
图4 仿真结果统计(重庆(υ1)为起点)
(2)以遂宁(υ2)为起点的仿真结果(程序运行51 s)如表7、图5所示。
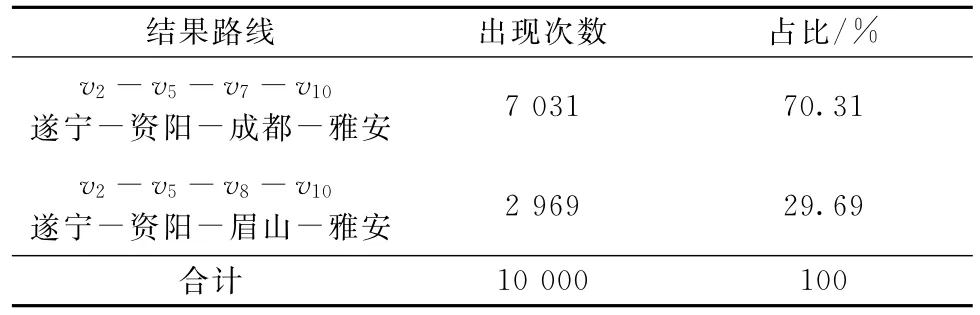
表7 仿真结果统计(遂宁(v2)为起点)
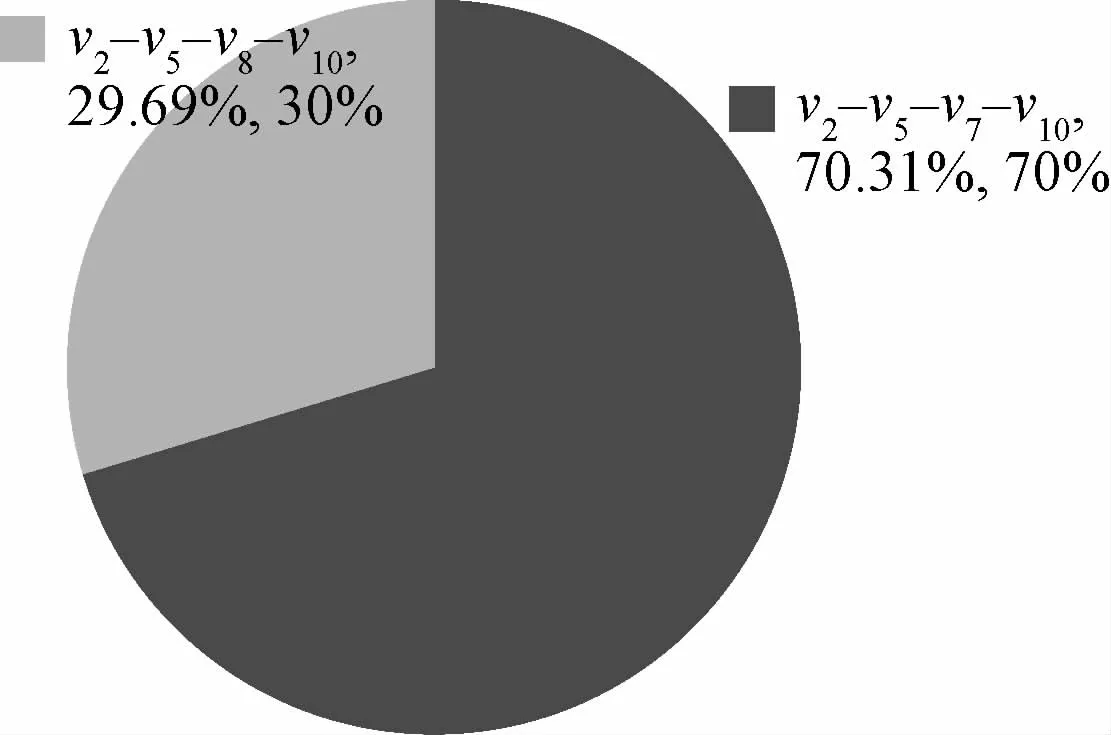
图5 仿真结果统计(遂宁(υ2)为起点)
(3)以内江(υ3)为起点的仿真结果(程序运行35 s)如表8、图6所示。
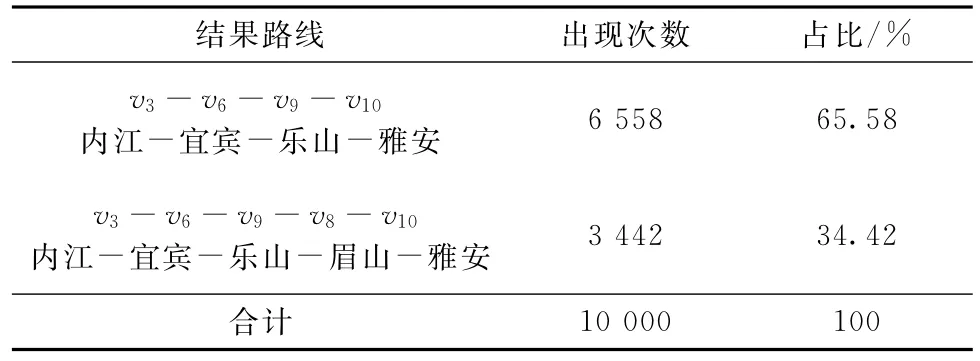
表8 仿真结果统计(内江(v3)为起点)
(4)以泸州(υ3)为起点的仿真结果(程序运行38 s)如表9、图7所示。
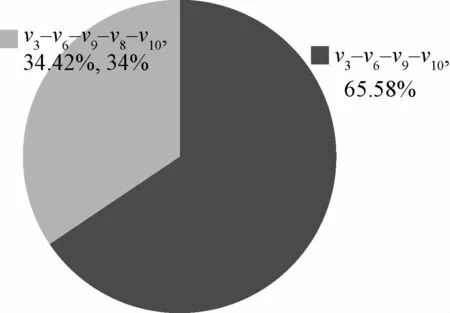
图6 仿真结果统计(内江(υ3)为起点)

表9 仿真结果统计(泸州(v4)为起点)

图7 仿真结果统计(泸州(υ4)为起点)
仿真结果显示,初始的最优路线只在一定的概率上会成为最终的车辆运行路线,需要结合路段属性变化的风险,综合选取、规划路线。
4 结语
救援任务进程中的不确定性,始终影响救援的进行。本研究中的临界值和稳定概率,为综合量化道路属性,梳理动态救援过程提供了依据及指导。综合相关学科的应用,本方法针对应急事件下次生事件不确定、路况复杂多变的特点,基于动态路径选择方法,指导救援过程中实时选择最优路线,将救灾过程的非常有限的物流资源尽可能充分利用,并规避风险,整体上提高救援效率,为动态救援决策提供有益思考。最后,通过算例分析进行验证。该方法下,需要多种学科技术的配合,各个学科之间如何更紧密协调,各种门类的数据如何更紧密衔接,以及如何更合理利用仿真数据,分析每个路线的特点,以合理规划物资运输,仍需未来的进一步研究。

