有限预知信息下集装箱码头泊位与岸桥联合在线调度
郑斐峰,乔龙亮,黄基诞
(东华大学 旭日工商管理学院,上海 200051)
根据英国航运咨询公司德鲁里(Drewry)2015年的CPI报告,全球班轮准班率连续两月下滑;最新的数据显示,亚欧、跨太平洋和跨大西洋航线的总体准班率从2014年10月的62%,11 月的64%下降至12月的58%。12月份的准班率也是2014年8月(55%)以来的最低水准[1]。当班轮出现延误之后,要想赶上船期表所计划的时间点,承运人需要付出巨大的额外燃油成本。此时,节省燃油、降低航次成本可能是其最佳的选择,从而导致了准班率的一定下降。站在港口角度,为了保障码头关键资源的利用率,往往通过增加服务加班船来应对主干船舶准班率的下降。在包括上海洋山港三期码头的一些港口运营中,加班船的具体调度往往不在港口的事先计划表中,这意味着对于港口,加班船具有较强的动态到达、实时服务的特征。考虑到泊位和岸桥是码头最为关键的两种调度资源,本文将针对这两种资源进行服务加班船的情形设计联合调度优化方案。
国内外许多学者对泊位分配(Berth Allocation Problem,BAP)、岸桥分配(Quay Crane Assignment Problem,QCAP),以及泊位与岸桥的联合分配调度(BAP-QCAP)等问题开展了大量研究[2-4]。Imai等[2]将泊位资源划分为离散、连续和混合型等3种类型,其中,一个混合型泊位在每个时刻要么服务一艘大型船舶,要么可以同时服务2~3艘小型船舶。例如,深圳蛇口的妈湾港根据码头地理特征采用的就是混合型泊位设计。对于BAP-QCAP 联合调度问题,Yang等[5]运用两阶段决策思想,采用两个内循 环 分 别 求 解 BAP 和 QCAP 子 问 题。Turkogullari等[6]对于包括船舶靠泊位置偏离值、等待时间和离港延迟时间的总成本优化目标构建整数规划模型。Xiao等[7]将已抵港的船舶根据服务状态划分为3类,并采用滚动时域求解算法进行求解。Vacca等[8]假设船舶服务时间取决于所分配岸桥数量,对所构建模型设计了分枝定价精确算法。一些学者考虑了调度过程中的干扰因素并构建相关模型展开研究。孙彬等[9]对于离散泊位且船舶抵港时间不一的调度情形,探讨了不确定因素的影响作用,对于最小化所有船舶总延误时间的优化目标设计了具有系统鲁棒性的调度策略。曾庆成等[10]对于连续型BAP-QCAP 问题,着重探讨了不确定干扰因素对调度过程的影响情况以及应对策略,建立了两阶段干扰管理决策模型。
现有的研究大都假设船舶需求信息事先全部已知,然而,通过上海洋山港的实地调研发现,因为加班船的大量存在,即使是上海洋山港大型深水码头,其船期表也是每天动态调整并安排许多泊位用于服务新抵港的加班船;在其排期密度表中,加班船的服务数量比例甚至达到1/3。加班船不同于主干船的服务特点,后者提前至少一个工作日就确定准确抵港时间,并在码头制定服务计划之前提早一天抵港并在锚地等待;加班船的服务具有明显的动态实时特征,这源于码头事先并不制定每艘加班船的具体服务时间计划,只是提供一定的泊位和岸桥资源供所有加班船使用的做法。因此,对每一艘加班船的服务安排,码头泊位与岸桥资源的调度显现出了很强的实时性。
Zhang等[11]将在线理论分析框架引入了集装箱码头调度问题,对上述船舶抵港时间顺序不确定的情形进行刻画,并探究了岸桥的动态分配优化方案。结合岸桥具有不可交叉移动的操作特征,以最大完工时间为优化目标构建了over-list在线模型,并给出了渐近竞争比为m/[log 2(m+1)]的最优在线策略,其中m为岸桥数量。在线理论主要用于刻画现实中,决策者无法获知问题的全部信息而又必需进行实时决策的一类多次决策问题。决策者只能逐步获取信息,同时根据已有的信息对服务请求作出回应,其决策效果通常是与信息完全已知情形下的最优效果进行比较。
本文采用Zhang等[11]的建模方法,运用在线理论来刻画泊位与岸桥的联合调度,根据船舶动态到达特征构建相应的online-oner-list在线模型。结合码头事先掌握一部分待服务船舶的信息的实际情况,构建有限预知信息下的泊位与岸桥联合调度在线模型,并探讨仅预知后续一艘船舶需求信息的特定情形,该研究有助于对预知多艘船舶的一般情形设计调度计划。带有预知信息的在线调度模型在生产调度等领域已有不少相关研究。Mandelbaum等[12]探究了平行机环境下,在线策略安排每个请求时预知后续h个请求信息的情形,研究结论表明,预知能力可以改进在线策略的竞争性能。Zheng等[13]考虑了决策时预知后续LD(≥0)个单位时间内所有到达请求的在线模型,对于可中断和不可中断两种情形分别探讨了预知能力为0≤LD≤2和0≤LD≤1的在线策略。
1 问题描述与基本定义
1.1 问题描述及模型假设
对于集装箱码头混合型泊位,由于受限制于岸线地理条件约束,其泊位岸线长度通常约在300~400 m,而每个岸桥自身宽度约为60 m,加上操作时的安全距离要求,故一个混合型泊位一般配置不超过6个岸桥,本文主要考察配置5 个岸桥的情形。对于加班船,其长度一般处于100~300 m。鉴于此,考虑如下的混合型泊位参数:该泊位可以同时靠泊1艘大船与1 艘小船,或者同时靠泊3 艘小船。为了方便表述,将这一混合型泊位刻画为左、中、右3个相邻的小泊位,从而小船(小请求)占用1个泊位而大船(大请求)占用2 个相邻泊位。在onlineover-list模型下,请求信息在零时刻逐个到达,决策者在每个请求ri释放时需立即决策其泊位及岸桥的分配,以及确定服务时间段,决策做出之后不可更改;在预知未来1个请求的情景下,在线策略在rn释放时即可获知序列长度即n取值。后文讨论基于如下5个基本假设:
(1)所有岸桥共享一条平行于泊位的移动轨道,因而每个岸桥左右相对位置始终不变。
(2)系统中只有两种请求,小请求、大请求的任务量分别为1和Δ(≥2),分别记ri=1和ri=Δ。
(3)左、中、右这3个离散泊位记为b1、b2、b3,从左至右的岸桥标为q1、q2、q3、q4、q5。在任一时刻,每个泊位及岸桥只能服务1个请求。小请求占用1个泊位且至多由2个相邻岸桥进行服务,大请求占用2个相邻泊位且至多由4个相邻岸桥进行服务。
(4)若请求ri由m i≥1个岸桥进行服务,则其服务时长等于ri/mi[8]。
(5)当请求ri(1≤i≤n-1)释放时可以预知下一个请求ri+1的信息;rn释放时可得知序列长度n的值。
模型的优化目标是最小化最后一艘船舶的完工时间。运用四参数描述法[3],将本文所构建的上述模型标记为

其中:hybr表示混合型泊位;3B、5QC表示3个离散泊位和5个岸桥资源;online-over-list表示请求逐个释放的在线模型;LD=1表示在线策略可以预知后续一个请求;Cmax为最大完工时间的目标函数。
1.2 竞争比定义及参数符号说明
一般运用竞争分析方法来求解在线问题,即假定存在一个事先掌握所有请求信息的离线敌手,通过控制请求的输入序列,使得在线策略执行性能尽可能的差。通常采用竞争比这一指标来度量在线策略的性能[14]。对于某一在线策略A,定义ΩA为其所有可能的请求输入序列的集合;给定任一序列σ∈ΩA,令Cmax(σ)为策略A服务完成序列σ的最大完工时间,C*(σ)为信息完全的情形下最优方案对应的目标函数值。将策略A的竞争比定义为
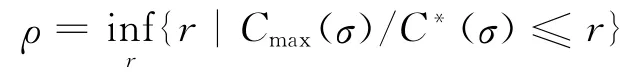
称A具有竞争比ρ或称A是ρ-竞争的。用竞争比下界表示所有在线策略对于该问题可能达到的最小竞争比。如果某一个在线策略的竞争比达到了竞争比下界值,则称其为最优在线策略。
下面列出模型讨论中主要运用的变量符号:
Cmax(σ)——在线策略的目标函数值
C*(σ)——离线策略的目标函数值
ti,1——ri释放时至少一个泊位完成此前分配至该泊位的所有请求的最早完工时间
ti,2,ti,3——ri释放时2、3个连续泊位完成此前分配至各自泊位所有请求的最早完工时间
Ci,j(1≤j≤3)——ri释放时b j泊位完成此前所分配的所有请求的最早完工时间
si,ei—— 请求ri的服务开始时间和结束时间
T a= [t1,t2)—— 在线策略分配大请求ri导致某一泊位服务该请求前出现可利用空闲时间段T a,满足t2=si=t1+1/2;初始化T a= [0,0)
对于

模型,所设计的在线策略在服务事先将每个岸桥与具体泊位进行固定配置,即将左侧的2个泊位b1、b2分别配置2个岸桥q1、q2和q3、q4,而最右侧的b3泊位配置1个岸桥q5。因此,如果某个大请求被分配至泊位b2、b3,则将会由3个岸桥q3、q4、q5进行服务。下面将对大请求具有任务量Δ≥3和2≤Δ<3的两种情形分别设计调度策略。
2 Δ≥3的情形
2.1 在线策略设计
基于前面对岸桥与泊位两种资源的固定配置方案,在线策略只需决策分配请求至哪几个泊位以及相应的服务启动时间。下面给出在线策略GR1(Greedy-1)的具体描述。
策略GR1若ri=rn,由于预知没有后续请求,故分配该请求至某一泊位以最小化Cmax。若有多个泊位均可导致相同目标函数值,则分配给下标最小的泊位;否则,若1≤i<n,由于预知后续请求ri+1,分如下两种情形进行决策。
C1ri=Δ。对于ri+1=1 或Δ,令启动时间si=ti,2,将ri分配至左边2个泊位b1、b2。
C2ri=1。
C2.1Ci,1-Ci,2=1/2。令si=Ci,2,将ri分配至b2泊位;
C2.2Ci,1=Ci,2。若ri+1=1,则令si=Ci,1,将ri分配至b1泊位;若ri+1=Δ,则令si=Ci,3,并将ri分配至b3泊位。
根据C2.1、C2.2 两种情形,若ri(1≤i<n)是小请求且被分配至b1泊位,则根据情形C2.2可知下一请求ri+1=1,从而ri+1满足C2.1条件并被分配至b2泊位。ri+1分配之后,b1、b2泊位同时从ei+1时刻进入空闲状态。因此,任意一个大请求ri=Δ释放时均有Ci,1=Ci,2。上述分析表明,b1、b2泊位及相应的4个岸桥在完成其所分配的所有任务之前不会出现空闲状态。
2.2 策略GR1的竞争分析
下面的定理给出策略GR1在Δ≥3情形下的竞争性能。
定理1对于问题

当Δ≥3时,策略GR1具有竞争比5/4。
证明给定任一请求输入序列σ= {r1,r2,…,rn},令Cmax(σ)为策略GR1的最大完工时间,C*(σ)为离线最优方案对应的目标函数值。根据GR1策略描述,所有大请求均被分配至左边2个泊位b1、b2,而且在完成最后一个大请求之前,左边2个泊位与4个岸桥一直处于服务状态。下面根据最后一个请求rn的分配结果讨论两种情形:
(1)rn分配至b1或b2泊位。
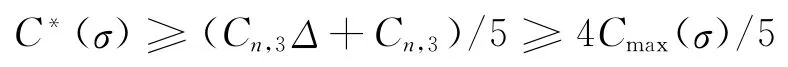
②rn=1。由于rn分配至b1或b2泊位,其加工长度为1/2。如果Cmax(σ)=Cn,3(>en),则分析同情形①;否则,如果Cmax(σ)=en= min{Cn,1,Cn,2}+1/2,当序列σ包含至多1 个大请求时,容易验证Cmax(σ)/C*(σ)≤5/4。当σ包含至少2个大请求时,由于大请求均分配至泊位b1、b2,min{Cn,1,Cn,2}≥2Δ/4≥3/2,同时,Cn,3>min{Cn,1,Cn,2}-1/2≥1(否则,rn将分配至b3泊位,矛盾),故

(2)rn分配至b3泊位,表明rn=1。根据前一个请求rn-1的大小分为如下两种情形:
③rn-1=Δ,表 明Cn,1=Cn,2。如果Cmax(σ)=Cn,1,分析同上述①中Cmax(σ)=en的情形;反之,如果Cmax(σ)=Cn,3+1,则Cn,1>Cn,3+1/2=Cmax(σ)-1/2(否则,rn将分配至b1泊位,矛盾)。在该情形下,若Cn,3=0,则Cmax(σ)=1,表明序列σ仅由1个小请求和1个大请求组成,从而C*(σ)=Cmax(σ);否则,若Cn,3≥1,则Cmax(σ)≥2,从而可得

④rn-1=1。如果rn-1满足策略C2.1情形而分配至b2泊位,则Cn,1=Cn,2。当Cmax(σ)=Cn,1时,C*(σ)≥4Cmax(σ)/5;当Cmax(σ)=Cn,3+1<Cn,1+1/2时,结合Cn,3+1/2<Cn,1与Cn,1<Cn,3+1,可以推出,Cn,3≥1(否则,1/2<Cn,1=Cn-1,1<1,即0<Cn-1,2= (Cn-1,1-1/2)<1/2,不等式矛盾),从而
C*(σ)≥(4Cn,1+Cn,3+1)/5≥4Cmax(σ)/5
如果rn-1满足策略C2.2情形而分配至b1泊位,则Cn,1=Cn,2+1/2。由情形(2)的条件知,Cmax(σ)=Cn,1>Cn,3+1(否则,rn将分配至b2泊位,矛盾),从而

综上所述,对于所有情形,均有Cmax(σ)/C*(σ)≤5/4成立。定理得证。 证毕
3 2≤Δ<3的情形
3.1 在线策略设计
对于2 ≤Δ<3 的情形,设计给出在线策略GR2(Greedy-2)。在该策略中,1个大请求ri(=Δ)的分配可能导致b1或b2泊位在服务该请求之前产生一个空闲时间段[t1,t2)= [t1,si),相应的空闲泊位记为bT。若0<t2-t1<1/2,则该时段长度不足以服务后续释放的任一小请求,记这一不可利用时段为Tw;若t2-t1=1/2,则该时段长度足以服务后续释放的1个小请求,将这一可利用时间段记为Ta。初始化Ta=Tw= [0,0)。下面给出策略GR2的具体描述。
策略GR2若ri=rn,由于预知没有后续请求,分配rn至某个泊位以使Cmax最小,若有多个泊位均导致相同的Cmax,则分配rn至下标最小的泊位;否则,若i<n,分两种情形调度:
介绍一部研究天然气产业的专著:《低碳经济下中国天然气产业发展战略》… ……………… 周 鹏(6.封三)
C1ri=Δ。若i=1且r2=1,或者i=2且r1=1,则令si=0,将ri分配至b2、b3泊位;否则,令si=max{Ci,1,Ci,2},将ri分配至b1、b2泊位。若Ci,1-Ci,2=1/2,则令b T=b2且

若0<|Ci,1-Ci,2|<1/2,则令

C2ri=1。若T a= [t1,t2)≠[0,0),则令si=t1,将ri分 配 至b T泊 位 并 重 新 设 置T a= [0,0);若ri+1=Δ且max{Ci,1,Ci,2}-Ci,3+Δ/4≥1,则分配ri至b3泊位且令si=Ci,3;否则,若上述两种情形均不满足,则不论ri+1=Δ或1,按如下两种情形进行调度:
C2.1ti,1=ti,3或ti,1<ti,2=ti,3。令si=Ci,1,将ri分配至b1泊位;
C2.2ti,1=ti,2<ti,3或ti,1<ti,2<ti,3。令si=ti,2,将ri分配至b2泊位。
给定任意请求输入序列σ= {r1,r2,…,rn},根据C1情形,只有在r1=Δ且r2=1或r1=1且r2=Δ的两种情形下,序列中的第1个大请求才被分配至右侧2个泊位;否则,所有大请求均分配至左侧2个泊位。同时,当且仅当分配第1个大请求至右侧2个泊位时,才可能在分配第2个大请求时产生唯一的T w时间段,如图1(a)、(b)中的阴影区域所示,其中,阴影的高度表示空闲时间的长度。在图1中,横轴表示3个相邻泊位,纵轴表示时间,每一个矩形表示一个船舶服务请求,矩形高度即为该请求实际服务的时长。对于左侧b1和b2这2个泊位,任意2个相邻大请求之间若存在空闲时段,则根据C2.1情形,必定是后一个大请求释放前在b1泊位分配了一个小请求,即该空闲泊位b T必定是b2,对应空闲时段Ta的长度等于1/2,如图1(c)中的阴影区域所示。综上所述,GR2策略所产生的加工序列中至多有1个T w时段。
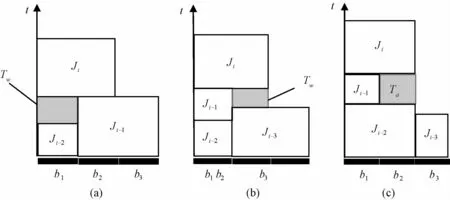
图1 两类空闲时间段Ta 和T w 示意图
3.2 策略GR2的竞争分析
下面的定理给出了策略GR2在2≤Δ<3情形下的竞争比结论。
定理2对于问题

当2≤Δ<3时,策略GR2具有竞争比5/4。
证明给定任一请求输入序列σ= {r1,r2,…,rn},令Cmax(σ)为 策 略GR2 的 最 大 完 工 时 间,C*(σ)为离线最优方案对应的目标函数值。根据序列σ包含的大请求数量讨论如下3种情形:
(1)序列σ中无大请求。根据C2.1和C2.2情形 可 知,r1,r2,…,rn-1均 分 配 至 左 边2 个 泊 位 即Cn,3=0。若rn-1分配至b1泊位,则rn将分配至b2泊位,b1、b2泊位的完成时间相同,从而Cmax(σ)=Cn,1且C*(σ)≥4Cmax(σ)/5;若rn-1分配至b2泊位且rn
分配至b3泊位,则分析同上;若rn-1分配至b2泊位且rn分配至b1泊位,因为Cn,3=0,所以Cn,1=1/2(否则rn将分配至b3泊位)且σ中仅由3个小请求组成,此时,C*(σ)=Cmax(σ)=1。
(2)序列σ中有且仅有1个大请求。在该情形下,T w= [0,0)。
①r1=r2=1。不妨设rk=Δ(2<k≤n),根据k的取值分为如下3个子情形:
(a)k=3<n。则s3=C3,1=C3,2=1/2。由于Cn,1≥Cn,2≥e3≥1及Cn,3=0,rn必 定分配 至b3泊位。对Cn,1=Cn,2与Cn,1=Cn,2+1/2两种情形,均可得C*(σ)≥4Cn,1/5=4Cmax(σ)/5。
(b)3<k=n。由于min{Cn-1,1,Cn-1,2}≥1/2,Cn-1,3=0且Cn-1,1+Δ/4≥1,表明rn-1必定分配至b3泊位即Cn,3=1。如果rn分配至b1、b2泊位,不论分配后是否Ta≠[0,0),均有Cmax(σ)=Cn,1+Δ/4且C*(σ)≥4Cmax(σ)/5;如果rn分配至b2、b3泊位,则Cn,1=Cn,2+1/2,Cmax(σ)=Cn,2+Δ/3,且
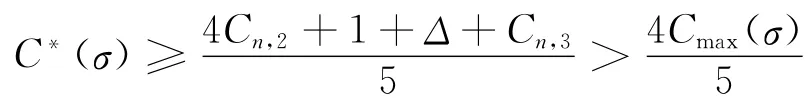
(c)3 <k<n。类似于(b)情形的分析,有Cn,3=1。若rn分配至b1泊位,则
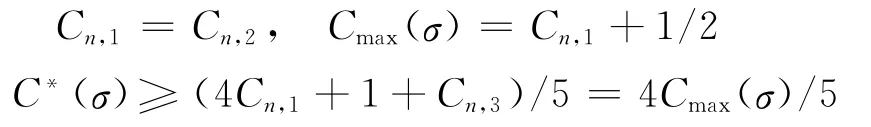
若rn分配至b2泊位,则

若rn分配至b3泊位且Cmax(σ)=Cn,1,分析同上;若rn分配至b3泊位且Cmax(σ)=Cn,3+1=2,则


②r1、r2中有且仅有1个大请求。则该大请求必定分配至泊位b2、b3,根据C2.1和C2.2情形,rn之前的所有小请求均分配至b1或b2泊位,表明Cn,3=Δ/3。
(d)rn分配至b1或b2泊位。结合2/3≤Δ/3<1与Cn,3=Δ/3可得,Cn,1≤3/2 且Cn,2≤Δ/3+1/2(否则,rn分配至b3泊位),从而序列σ由1个大请求和至多5个小请求组成即n≤6。对于2≤n≤6,均可验证Cmax(σ)/C*(σ)<5/4。
(e)rn分配至b3泊位。结合(d)中情形的分析知,n>6且有

由于|Cn,1-Cn,3|<1/2,故

(3)σ中至少包含2个大请求。
①T w= [0,0)。若r1、r2中有且仅有1个大请求,由T w= [0,0)可推断,σ中仅有2个大请求且rn=Δ分配至b2、b3泊位(否则,由C1情形知,第2个大请求将分配至b1、b2泊位,从而T w≠[0,0),矛盾)。Cmax(σ)=Cn,2+Δ/3,由于Cn,3=Δ/3,故

下面讨论r1=r2=1的情形。在该情形中,序列σ中的所有大请求均分配至b1,b2泊位,除非rn=Δ。
(f)rn分配之后,Ta≠[0,0)。则在该Ta出现后的所有请求均为大请求;同时,根据C2情形可以判定Cn,3≥1(否则,若Cn,3=0,则Ta期间b1泊位上加工的小请求ri由于满 足ri+1=Δ且max{Ci,1,Ci,2}-Ci,3+Δ/4≥1将被分配至b3泊位)。由于T a的空闲时长等于1/2,在该时段内2个空闲岸桥的总加工能力为2×(1/2)=1,故
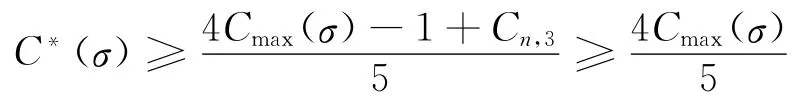
(j)rn分配之后,Ta=[0,0)。若rn=Δ且分配至b1、b2泊位,则Cmax(σ)=Cn,1+Δ/4且C*(σ)≥4Cmax(σ)/5;若rn=Δ且 分 配 至b2、b3泊 位,则Cmax(σ)=Cn,2+Δ/3,结合1>Δ/3与Cn,1-Cn,2=1/2,

若rn=1且rn分配至b1泊位,则

(否则,若Cn,3<Cn,1-1/2,rn会被分配至b3泊位),

若rn=1 且分配后有Cmax(σ)=Cn,1,则C*(σ)≥4Cmax(σ)/5;若rn=1且分配至b3泊位后,有Cmax(σ)=Cn,3+1,则Cn,2>Cn,3+1/2。类似于(c)情形的分析,有Cn,3>1,从而

②T w≠[0,0)。此时,r1、r2中有且仅有1个大请求且被分配至b2、b3泊位。根据定义,T w只出现在b1或b2泊位。在T w之前,b1泊位只服务小请求且加工长度均为1/2,而b2泊位所分配的请求除了第1个是大小为Δ/3的大请求,其他均为小请求。因此,若T w在b1或b2泊位,其长度分别为Δ/3-1/2和1-Δ/3。结合2≤Δ<3,max{Δ/3-1/2,1-Δ/3}≤Δ/6,表明在T w期间2个空闲岸桥的总加工能力至多为Δ/3。
(k)rn分配之后,Ta≠[0,0)。则在该T a出现后的所有请求均为大请求。类似于(f)情形的分析可知,Cn,3≥Δ/3+1,Cmax(σ)=Cn,1+Δ/4。由于T w与Ta时段内2个空闲岸桥的总加工能力分别不超过Δ/3和1,故
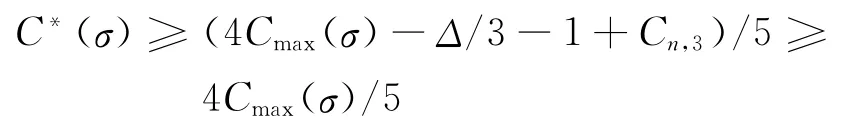
(l)rn分配之后,Ta=[0,0)。已知Cn,3≥Δ/3且Tw期间2个空闲岸桥总加工能力至多Δ/3。若rn=Δ且分配至b1、b2泊位,则Cmax(σ)=Cn,1+Δ/4且
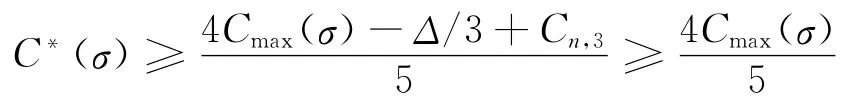
若rn=Δ且分配至b2、b3泊位,则Cmax(σ)=Cn,2+Δ/3,结合条件1>Δ/3与Cn,1-Cn,2=1/2,
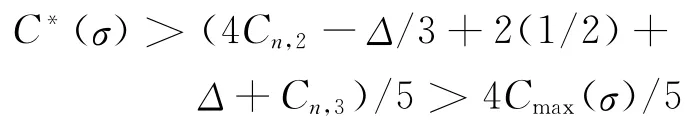
若rn=1且分配至b1泊位,则

从而
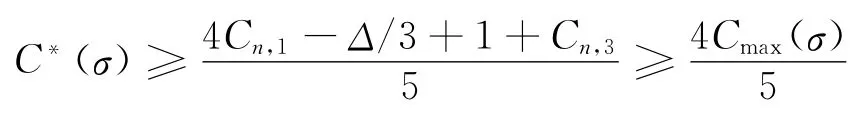
若rn=1且分配后有Cmax(σ)=Cn,1,则Cn,3≥Δ/3且
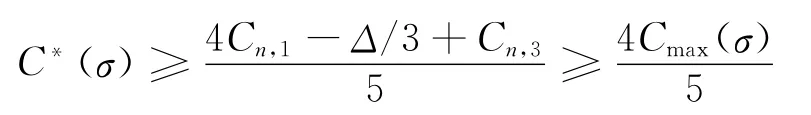
若rn=1且分配至b3泊位后有Cmax(σ)=Cn,3+1,则Cn,1=Cn,2>Cn,3+1/2。当Cn,3=Δ/3时,由于Cmax(σ)=Δ/3+1,且σ中包含至少2个大请求和2个小请求,结合C*(σ)≥min{2Δ/3,1+Δ/4}可得,Cmax(σ)/C*(σ)≤5/4;当Cn,3≥Δ/3+1时,

综上所述,对于任意序列σ,总有Cmax(σ)/C*(σ)<5/4。定理得证。 证毕
结合定理1、2的结论,对于

模型可设计如下调度策略:对于Δ≥3的情形采用GR1策略,对于2≤Δ<3的情形采用GR2策略。由定理1、2可知,该调度策略对于上述模型具有竞争比5/4。
4 竞争比下界分析
下面给出泊位与岸桥联合调度模型的竞争比下界,以及无预知能力时相应的竞争比下界。
定理3问题

的竞争比下界为5/4。
证明要证明该定理,只需设计一个请求输入序列σ,使得对于任一在线策略A满足不等式Cmax(σ)/C*(σ)≥5/4,其中,Cmax(σ)和C*(σ)分别为策略A所产生服务序列的最大完工时间、离线最优方案下的目标函数值。序列σ包含至多3个请求且r1=r2=1。策略A在分配r1时预知r2=1。若A分配1个岸桥服务r1,则e1=1,σ={r1,r2},从而Cmax(σ)≥1。最优方案将各分配2个岸桥分别服务2个请求,C*(σ)=1/2且Cmax(σ)/C*(σ)≥2;反之,若A分配2个岸桥服务r1,则r3=Δ且σ={r1,r2,r3}。因为r3需占用2个相邻泊位,所以Cmax(σ)≥min{Δ/3,1/2+Δ/4}。最优方案将分配1个岸桥服务前2 个请求,分配4 个岸桥服务r3,C*(σ)=max{Δ/4,2}。令Δ=8,从而Cmax(σ)/C*(σ)≥5/4。定理得证。 证毕

定理4问题的竞争比下界为4/3。
证明相同于定理3的证明思路,只要设计一个请求输入序列σ,使得对于任一在线策略A满足不等式Cmax(σ)/C*(σ)≥4/3即可。序列σ包含至多2个请求且r1=1。若A对r1只分配1个岸桥,则σ= {r1};Cmax(σ)≥1 而C*(σ)=1/2,从 而Cmax(σ)/C*(σ)≥2;反之,若A分配2个岸桥服务r1,则r2=Δ且σ={r1,r2}。由于只有5个岸桥,策略A要么分配3个岸桥服务r2,要么对r2分配4个岸 桥 且 最 早 从1/2 时 刻 启 动 服 务,Cmax(σ)≥min{Δ/3,1/2+Δ/4}。最优方案则分别分配1个和4个 岸桥来服务请求r1和r2,C*(σ)= max{Δ/4,1}。令Δ=6,从而Cmax(σ)/C*(σ)≥4/3。定理得证。 证毕
结合定理1~4可知,即使赋予十分有限的预知能力,即只能预知后续一个请求,在线策略的最坏情形理论竞争性能也是能够得以改进的。
5 数值分析
针对前面所讨论的Δ≥3和2≤Δ<3两种情形,下面通过数值计算进一步验证策略GR1 和GR2的平均执行性能。主要考察不同的序列长度,以及大请求的不同任务量对相应策略的平均性能有何影响,同时,对比分析理论证明结果与模拟分析数值结论的差异。这里,对每一种参数设置情形,利用计算机分别随机产生10 组请求序列,并计算GR1(或GR2)策略的解与最优解对应目标函数值在10组序列中的平均比值,借以判断在线策略的平均执行效果。具体的数值计算设置和分析如下:
首先,对于Δ≥3 的情形考察在线策略GR1。给定大请求的任务量Δ=5,设置序列长度n分别等于50、100、150、200、250、300、350、400、450和500;针对上述每一种序列长度分别随机产生10组序列,并计算GR1策略所给出的目标值与最优值的平均比值,得到表1所示的结果。
将表1的数据在图2中用折线图进行表示。由图2可以看出,对于不同的序列长度,策略GR1所得到的平均竞争比取值在[1.048 7,1.098 4]区间内小幅波动,并无明显的增减规律,表明序列长度对于策略的平均执行性能基本上没有影响;其次,所有的值均明显小于理论竞争比1.25,说明策略的实际执行效果明显优于理论结果。

表1 Δ=5时不同序列长度下的平均竞争比数值

图2 策略GR1平均竞争比值随输入序列长度的变化趋势图
下面考察大请求任务量Δ的不同取值对策略GR1平均竞争比值的影响。分别取Δ=3、6、9、12、15、18、21、24、27 和30,并设定序列长度n=100(对于其他序列长度,结论相似)。对每一个Δ取值分别随机产生10组序列并计算平均竞争比值,得到表2所示的结果。将表2 的数据用折线图进行表示,如图3所示。

表2 序列长度n=100时不同Δ 取值下的平均竞争比数值
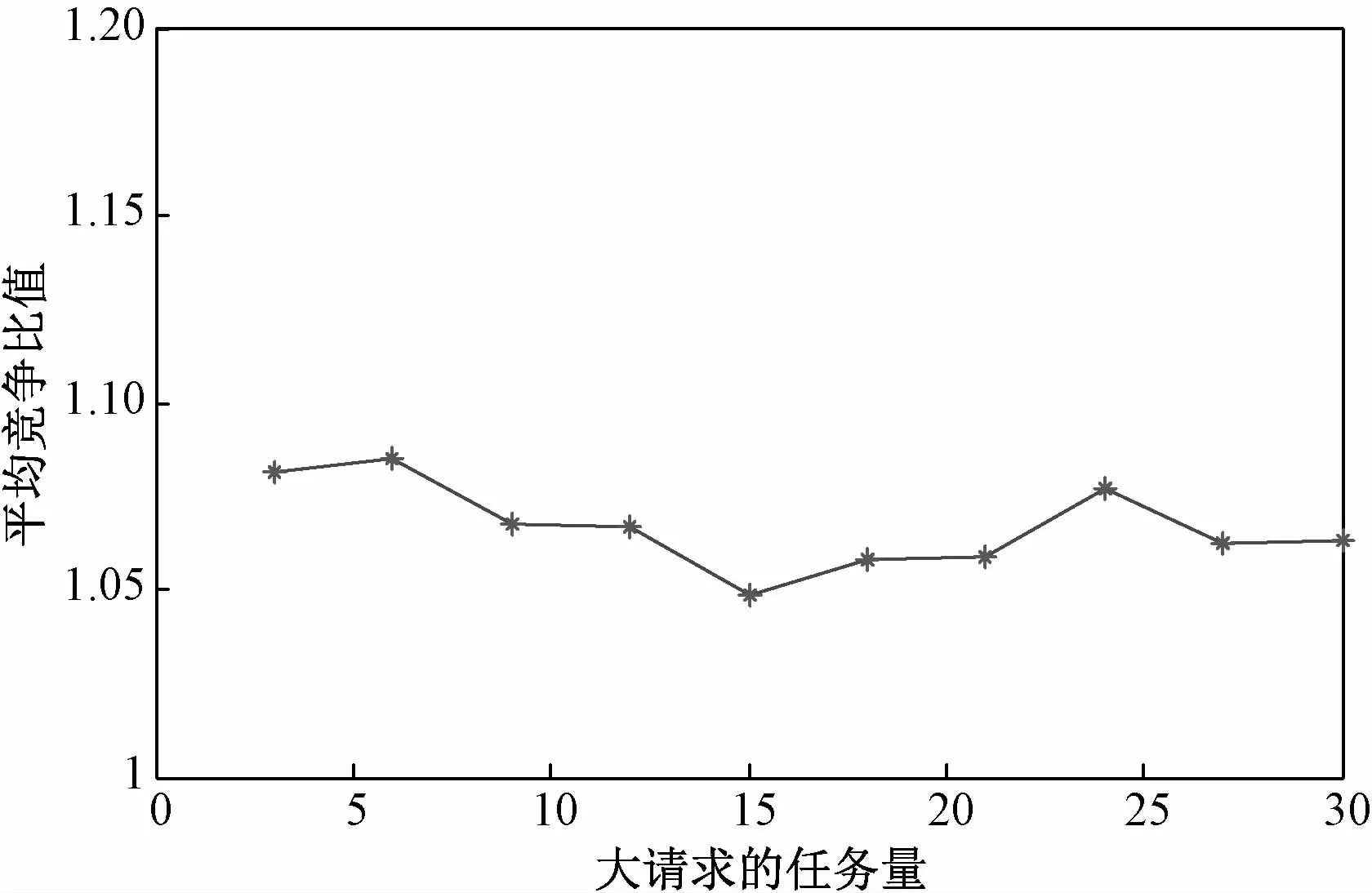
图3 策略GR1平均竞争比值随大请求任务量的变化趋势图
根据表2和图3,策略GR1的目标函数值与最优值的平均比值在[1.048 7,1.085 5]区间内小幅波动,且无明显的增减规律,表明大请求的大小对于策略的平均执行性能基本上没有影响;其次,所有的数值均明显小于理论结果1.25,表明该策略对于大请求的各种大小均具有良好的平均执行性能。
其次,对于2≤Δ<3的情形下在线策略GR2的考察思路同前,其分析结论基本相同于策略GR1的结果。设定大请求任务量Δ=2.4,针对前一情形的10种序列长度类似地计算GR2策略的平均竞争比值,结果如图4所示。策略GR2的目标函数值与最优值的平均比值在[1.051 2,1.058 1]微小区间内波动,波动区间整体小于策略GR1在Δ=5时的情形,表明策略GR2对于较小的Δ值在平均性能上略优于在Δ取值较大时所采用的GR1策略。
进一步,设定序列长度n=100,针对10种不同的Δ取值,即Δ=2.0、2.1、2.2、2.3、2.4、2.5、2.6、2.7、2.8和2.9,分别计算策略GR2的平均竞争比值,如图5所示。

图4 策略GR2平均竞争比值随输入序列长度的变化趋势图
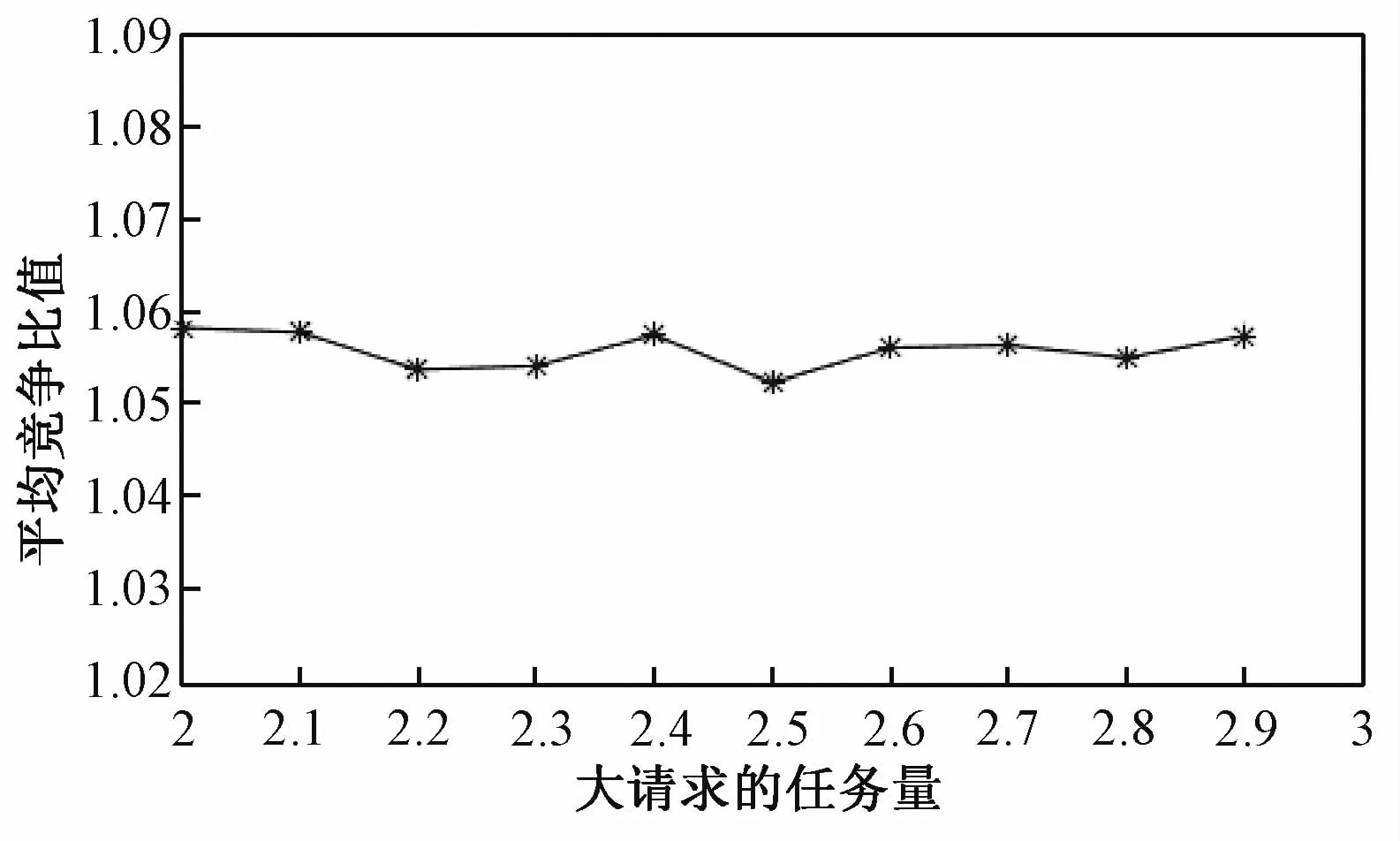
图5 策略GR2平均竞争比值随大请求任务量的变化趋势图
在图5中,策略GR2的平均竞争比值的波动区间为[1.052 3,1.058 3],这个波动区间同样略优于策略GR1对于不同Δ取值下的平均性能,其结论相同于前面对不同序列长度下的两种策略优劣的讨论;同时,策略GR2的平均竞争比值要明显优于理论竞争比5/4。
基于上述分析,策略GR1和GR2对于给定的某个大请求任务量取值,其平均执行性能均控制在最优值的1.1倍以内。这表明,2个在线策略具有良好的平均执行性能,其策略构建思路对于码头实践中的调度优化方案设计具有一定的指导作用。
6 结语
针对集装箱码头加班船作业的实时服务特征,运用在线理论构建了有限预知信息下的泊位与岸桥联合调度在线模型,探讨了一个混合型泊位布局,配置5个岸桥且仅有两种大小船请求的情形。对于预知未来一个请求的能力,设计出了具有最优竞争比5/4的在线调度策略;同时,分析指出,无预知能力下的在线策略竞争比不小于4/3,表明即使十分有限的预知能力也可以有效地改进在线调度策略的竞争性能。在后续研究中,将进一步探讨具有多个并行操作的混合型泊位,或者船舶任务量在一定范围内任意取值的更一般情形,探析新的模型性质并设计具有良好竞争性的在线策略。

