基于空间与技术异质性的能源基础设施选址决策
葛世龙,黄东梅,吴其阳,于可巧
(南京审计大学a.工程管理学院;b.组织人事部,南京 211815)
自20世纪90年代以来,全球气候变暖问题已被列为全球性十大环境问题之首,大力发展可再生能源被世界各国广泛认为是应对全球气候变化、保障能源安全、促进节能减排、实现可持续发展的共同选择[1-2]。近年来,我国先后颁布和制定了《可再生能源法》、《可再生能源中长期发展规划》、《中国应对气候变化国家方案》、《可再生能源发展指导目录》以及《新能源产业规划》等一系列法律和政策法规,在政府推动、危机驱动、市场拉动以及媒体鼓动等多种力量作用下,在能源领域进行了大量的投资,我国可再生能源取得长足发展,尤其新能源装机与发电已成为世界第一。中国政府及国家领导人高度重视可再生能源发展,指出要密切跟踪世界新一轮新能源发展方向,加强新能源技术研发,增加对新能源产业投资,积极发展核电、风电、太阳能发电等清洁能源。《能源发展战略行动计划2014~2020年》中明确指出,按照输出与就地消纳利用并重、集中式与分布式发展并举的原则,加快发展可再生能源,坚持统筹兼顾、因地制宜、多元发展的方针,有序开发可再生能源。这些都强调了能源技术的空间差异性和技术异质性特征。
风能、水能、太阳能发电是可再生能源中发展速度最快、前景最好的能源品种,它们各有特色,在时间和空间上具有互补性。Jacobson等[3]研究指出,未来将出现低成本的100%风能、水能和太阳能组成的系统,Clack 等[4]在指出Jacobson等研究结论存在重大缺陷的同时,认为构建一种由各种能源品种组成的广泛的投资组合以加快能源系统向零排放系统转变是可行的。随着可再生能源装机容量的大规模增加,我国可再生能源发展陷入“边建边弃”的怪圈,弃风弃光问题尤为严重。据统计,2015 年我国弃风弃光总量为386 亿k W·h,弃风弃光率为14.6%,2016年甚至高达700 亿k W·h。其原因包括:①缺乏统筹规划管理。我国能源供应和能源需求呈现倒挂局面,能源供需结构的空间差异性明显。②可再生能源异质性、间歇性显著。以风电、光电为代表的可再生能源发电的稳定性不仅表现在季节性差异,而且还反映在一天的不同时点差异,这种差异使得电力系统难以精确估计电网的供电量,进而影响电网的运行和调度。③调峰能力不足。区域电网调峰能力不足一直是制约我国风能太阳能发电上网的重要因素,这种矛盾又会被我国区域间的资源禀赋、能源需求和经济发展水平等方面的空间差异性加剧,导致可再生能源装机容量的进一步浪费[5-8]。为了解决这种矛盾和不稳定性就需要在考虑能源技术的异质性及互补性的前提下,综合电网规划、区域发展和经济环境等空间要素的差异性,进行科学合理地选址与布局。
为了应对全球气候变化与能源安全,提高能源供给质量和效益,化解和防范过剩产能,推进能源清洁开发利用,需要合理规划传统能源产能和可再生能源发展规模,合理布局能源基础设施。能源基础设施选址不仅需要考虑能源技术的异质性与互补性,而且还需要充分考虑能源需求、经济发展等空间要素,是一个复杂决策问题。一般地,可以借助专家知识及以往经验进行能源基础设施的选址决策,然而,区域经济发展水平、资源禀赋以及决策者偏好不一致,还是一个多指标、多准则问题,使用常规方法难以得到合意的决策结果。因此,本文提出一种结合网络分析法(ANP)和多目标规划的模型,利用ANP方法分析能源技术的异质性及其目标的重要性,解决多指标问题及指标之间的相关性。通过ANP分析所得权重构建多目标规划模型进行选址,以期为我国政府部门制定多能互补相关政策、解决弃风弃光问题提供决策支持。
1 文献综述
选址问题是一项战略性决策,其影响深远且持久。从最初的单一设施选址到多个设施选址,从直线、平面上的布局到网络上的规划,从确定的参数到随机的分布,来源于实践的选址研究逐渐从简单发展到复杂,从零散发展到系统,并随着应用背景的广泛变化不断丰富和发展,涉及物流设施选址、应急设施选址等[9-14]。
随着选址理论模型及其应用研究的不断深入,能源系统的选址也越来越受到关注,主要包括如下研究:
(1)空间因素对选址的影响研究。许多研究指出进行正确的空间分析(包括位置识别、合理选址和正确布局)可以减少环境影响。韦庆明等[15]在实证分析农村改水工程健康效应时,指出这种健康效应具有正向的空间溢出特征。空间分析在可再生能源可持续性领域应用越来越广泛,Mann 等[16]利用Logistic回归研究了Iowa风能发展的空间因素,涉及风速、土地利用、地质特征、输电线、道路和消费者分布等。Piyatadsananon[17]认为,在地面安装光伏电站的选址时需要考虑气候、电网、水资源、土地使用以及地形等空间因素,并指出这些因素可以通过GIS系统获得。Punt等[18]研究了海上风电场选址对海洋环境的影响,指出风电场的合理空间规划是经济与环境双赢的关键因素。Uyan[19]结合GIS和AHP方法研究了土耳其Karapinar地区的光电场的选址问题。Xu等[20]利用GIS技术分析了火电厂的位置识别与选址问题,对道路、燃料供应、电网可用性和土地利用等因素进行了空间分析。Venier等[21]基于地质、环境和社会经济因素,利用GIS合理性分析给出了沼气发电厂设立的潜在位置。在考虑农场规模大小和交通距离经济可行性的同时,利用空间统计分析法研究了沼气发电厂的最优选址。Noorollahi等[22]利用GIS分析了Markazi的风能选址问题。
(2)选址的定性指标及其分析方法研究。在分析空间因素对选址影响的文献均指出选址决策包含了多准则问题,在选址时考虑了许多定性因素,涉及技术、环境、经济、地理和政策等方面[21-24]。AHP广泛应用于多准则间的重要性比较[19,24-25],但AHP难以处理准则间的关联性,其他学者利用语言Choquet积分算子、模糊积分以及ANP等方法进行了研究[23,26-28]。由此可见,开发出一种有效的工具对于提高选址效率非常重要。
(3)选址的定量模型研究。许多文献通过构建数学模型定量化研究选址问题。Cheng等[29]将DEA与二元整数线性规划模型相结合用于建设项目选址的投资分析。Lv等[30]以经济增长、碳排放为目标,秸秆供需为约束,构建了一个多目标混合整数规划模型用于秸秆发电站的选址研究。Song等[31]建立了双层多目标规划模型用于火电厂的选址与布局优化问题。由于数学规划模型难以将定性因素考虑进去,也无法确切地给出多目标决策中各个目标的优先级,使得选址结果难以满足决策者的要求。
目标规划被认为是可以处理多目标问题的有效方法,已广泛应用于可再生能源规划、环境分析、可持续发展以及选址。Ramón等[32]构建了多源多汇网络,考虑多种可再生能源,假定每个备选点均可配置各种能源,但一个地方只能建一个发电厂,进而建立了目标规划模型用于可再生能源发电厂选址。Chang[33]改进了文献[32]中的模型,构建了一个多目标规划模型,考虑了电量、投资成本、减排量、创造的工作岗位、运行与维护成本以及距离安全和社会接受度等目标,用于分析可再生能源行业的电源规划问题。Ramón等[34]基于环境投入产出线性规划构建了一个考虑社会、环境、能源和经济目标的目标规划模型,并将其应用于西班牙环境政策分析,便于政策制定者检验不同的目标以实现可持续发展。Nixon等[35]利用目标规划分析了印度Punjab的热解装置的选址问题。基于股东对资本成本、投资回报期和生物制油及发电的生产成本的要求,同时考虑选址、设施大小和数量、下游能源应用以及原料加工的最优决策,从而实现供应链的最优设计。然而,由于存在不确定性以及信息不完全,决策者有时难以决定每个目标的特殊值。对于多重选择问题而言,目标之间的冲突无法由单一的目标规划解决,文献[33]中构建了多重选择目标规划可以满足决策者对多目标的需求。
(4)多能互补选址研究。能源技术具有异质性,需要充分考虑各种能源技术的优劣势,并考虑多能互补的优势,进行能源基础设施的综合选址[3-4,32-33]。Aydin等[36]利用GIS 分析了混合的可再生能源系统。Wu等[37]基于理想物元可拓法研究了风电混合电站的宏观选址问题。Vasileiou等[38]利用GIS与MCDM 方法研究了希腊海上风电和海浪能混合系统的选址问题。尽管如此,文献中较少考虑多种能源间的协同效应,以及与已有设施之间的协同,尤其当前弃风弃光现象严重的情况下,合理匹配多种能源及其合理选址对于经济发展、环境保护和可持续发展至关重要。
由此可见,现有文献对单一能源的选址问题已展开广泛的研究,尤其是风能、生物质、垃圾发电等新能源选址,文献中不仅强调了空间因素对能源选址决策的重要作用,而且还研究了多能互补系统选址问题。尽管现有文献对能源技术异质性和空间差异性进行了较为深入的研究,但是缺少对选址决策所涉及的多指标、多准则之间的关联性以及多能互补的协同效应的研究。本文通过ANP方法研究多指标、多准则的关联性问题,并确定指标的重要性程度,进而形成多重选择目标规划。在相关约束中考虑不同能源技术之间的协同效应,拓展了多能互补选址模型,便于决策者进行科学决策。
2 能源基础设施选址问题描述
2.1 能源基础设施选址的空间差异性及其评价准则
空间分析对于选址研究至关重要,许多研究指出进行正确的空间分析(包括位置识别、合理选址和正确布局)可以减少环境影响。这不仅充分考虑了区位差异,而且还结合了技术异质性。GIS被广泛应用于空间分析,也有许多文献从多指标、多准则角度来刻画选址的空间差异性,在可再生能源选择以及能源发电厂选址相关文献中对选址准则展开了广泛的讨论,文献[21-24]中总体可以归结为技术、经济、环境和社会等方面,文献[28]中还增加了政治方面。文中在能源基础设施选址分析时只考虑技术、经济、环境和社会4个准则,根据文献,这些准则由具体指标进行度量,衡量技术准则的指标包括效率、可靠性、资源可用性、投资能力、技术成熟度和技术风险;衡量经济方面的指标包括投资成本、运行和维护成本、研发成本、投资回报率和生产成本;衡量环境方面的指标包括温室气体排放、土地利用、噪声、生态系统影响和环境风险;衡量社会方面的指标包括社会效益、社会可接受度、工作创造和健康风险。由此可以形成选址的三级层次结构,如图1所示。

图1 能源基础设施选址的层次结构
图1中,第1层是能源基础设施选址的最终目标,第2层是准则层,分为技术、经济、环境和社会4个方面,第3 层是指标层,分别用于度量相应的准则。
2.2 能源技术的异质性及互补性分析
风能、水能、太阳能发电在可再生能源中占比最大,且发展速度最快、发展前景广阔,不同技术的资源条件不同,呈现出异质性,导致区域发展不平衡,需要因地制宜。同时,各种能源技术又在时间和空间上具有互补性,通过取长补短、合理布局能够提高能源保障能力,优化能源结构。因此,多能互补被认为是一种更高效、可靠的发电方式,在能源基础设施选址时考虑多能互补至关重要。在具体选址研究中,由于指标反映的空间差异性和技术异质性、互补性,研究指出,选址的决策准则之间存在着复杂的交互影响,如果用简单的AHP探析其内在含义,将使得决策不够准确[23,26-28]。由于存在关联性,图1 中的属性关系不再是简单的独立关系,它们有时相互依赖,有时会产生反馈效应,指标层的交互作用也会导致属性间的交互效果,其复杂关系如图2所示。
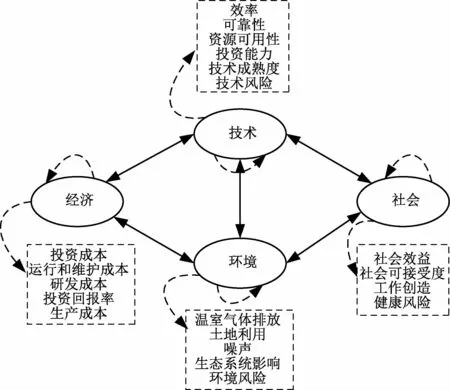
图2 准则及指标的网络关系
以社会与环境之间的交互关系为例来说明图2的网络关系。社会与环境之间的关系广受公众关注,生态系统的结构及功能的可持续性是由社会和环境系统的协同反馈作用形成的。一个地区的人口增长是由当地的环境容量所决定,相应地,人类活动也影响着物理和生物环境。环境承载能力是动态的,随着生命支持系统退化而降低,也会随着新的环境改善技术的使用而提高。
除此之外,能源技术的互补性主要体现在项目之间的关联性,主要包括3种类型:①资源相关性,是指能源基础设施项目间共享场地和电网设施,相同的人员等资源,同时实施两个或更多项目需要的资源,比单个实施这些项目需要更少的资源;②效益相关性,是指当两个相关的项目共同作用时,能产生协同效应,从而使总的效益提高;③技术相关性,是指在开发一个能源项目时需要开发一个相关项目。因此,在能源基础设施选址决策时不仅要关注资源的空间分布,还要关注技术关联性,进而可以共享有价值的资源,从而使得总的资源消耗减少。尤其在当前产能过剩、弃风弃电弃水严重的情形下,如何利用好与已实施项目间的协同问题,并考虑到资金分配的问题,对于提高资源利用率和效益至关重要。
2.3 能源基础设施选址的一般描述
能源基础设施选址问题是一个多源多汇问题,即多种能源技术、多个备选地址。本文基于文献[32-33],给出多源多汇网络的一般结构,设定m种能源技术,n-m个备选地址,如图3所示。
评估这m种可再生能源技术的指标可以从技术、经济、环境和社会等方面展开(见图1),包括发电量、投资成本、年CO2减排量、工作岗位创造、运行和维护成本以及电站的距离、社会可接受度等,可以根据实际情况获得相应数值,并结合国家能源规划和经济发展情景设定了理想值作为优化目标值。最后,得到可再生能源的选址决策。

图3 多源多汇网络
由此可见,关联性是能源技术项目的重要特性之一,关联性原理要求在能源基础设施选址时,不仅要考虑备选项目多属性间的关联性,还要考虑能源项目间、及其与已实施项目间的关联问题。本文通过ANP方法分析指标、准则的关联性,并得到众多目标之间的重要性排序。进而,考虑多能互补系统的协同效应,详细描述能源基础设施选址决策的多重目标约束及多种资源约束。最后,结合权重考虑各目标偏差的多重目标规划模型进行选址决策。
3 ANP与多重选择目标规划模型构建
本文利用ANP确定用于不同选址目的的定性评价指标的权重,建立多重选择目标规划模型对备选地址进行定量研究。因此,综合ANP 与多重选择目标规划模型研究能源基础设施选址的流程如图4所示。
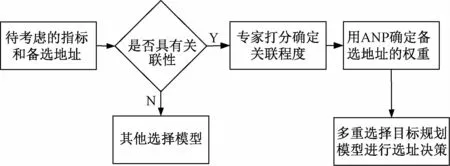
图4 ANP与多重选择目标规划模型分析流程
3.1 空间差异性和准则关联性的ANP分析
AHP方法广泛应用于多指标决策问题,它对于解决多层次、多目标的大系统优化问题很有效。在传统的AHP方法中,同一层次中的元素被认为是彼此独立的,这种递阶结构虽然给处理系统问题带来方便,同时也限制了它在复杂决策问题中的应用。实际的决策问题不具有很清晰的层次结构,因为它们涉及上、下层因素间的相互作用和依赖性问题。这样构造的问题就涉及一个反馈的过程,具有网络关系。因此,需用ANP 来解决项目及指标间的相关性问题。
能源基础设施选址的关联性分析一般过程包括:①识别值得考虑的多种指标,并建立指标的关系图,得到反映指标关联程度的关联矩阵;②确定指标间或项目间的影响程度,比较所有项目在每个指标下的重要程度,用1~9标度来衡量,反映在两两比较的重要性矩阵中;③得到全部备选地址的优先级别及其权重。
3.2 多重选择目标规划
目标规划能够处理单个主目标与多个目标并存,以及多个主目标与多个次目标并存的问题,通过平衡各标准目标的实现程度,使得每个目标函数的偏差之和最小。Chang[39]构建了多重选择目标规划,允许决策者为每个目标设定多重选择的预期水平,以防低估了决策。其模型形式为:
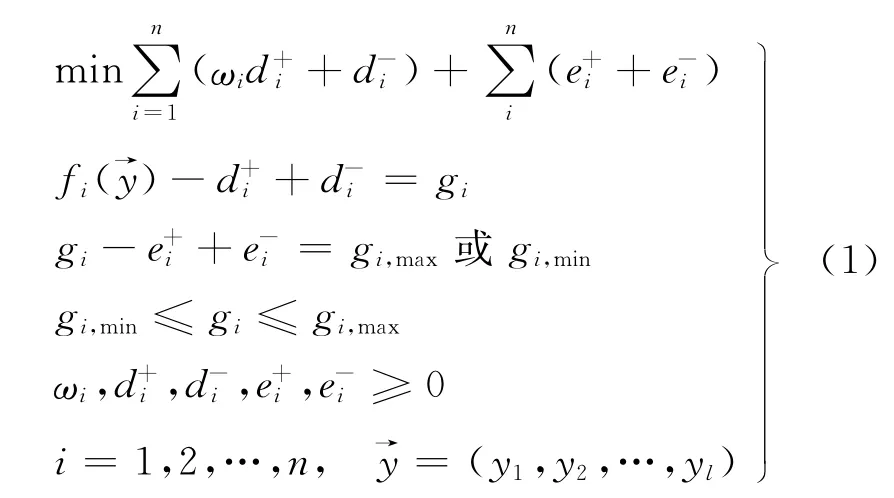
式中:ωi为目标函数的正偏差的权重,是由ANP方法计算所得;分别为第i个目标的正负偏差;n为目标的个数为针对第i个目标关于备选位置的线性函数;gi为第i个目标的预期水平,gi,max、g i,min分别为g i的上限和下限值分别为或的正负偏差值;m、l分别为能源种类和能源基础设施备选位置的数目,假设某些备选位置间存在着关联性,备选项目与已实施项目同样存在关联性。用A、B分别表示备选和已实施的能源基础设施项目编号的集合,记A= {1,2,…,m},B= {1,2,…,l};定义x i、y i为:
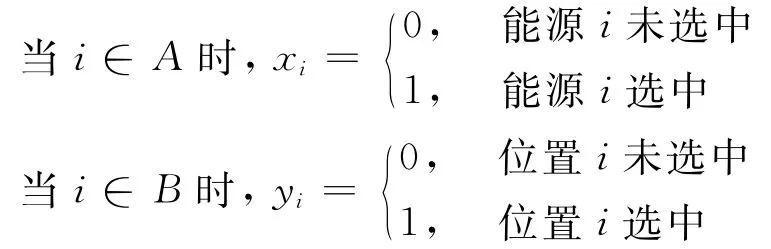
显然,多重选择目标规划是目标规划的线性形式,在达到预期目标的同时实现最优选址。
3.2.1考虑技术异质性和互补性的目标设定
在利用多重选择目标规划分析之前,需要明确设定的目标及各种约束条件。本文中的目标即是能源基础设施选址的准则(也可以直接设定评价指标为目标),在给定的决策环境中,要全部或部分达到的目标,即经济目标、环境目标、技术目标和社会目标[40]。系统约束是指对决策变量进行限制的条件,确保项目选择是可行的,如资源约束、强制性约束等。
(1)经济目标。根据前面分析可知,可以用电站总成本来度量经济目标,总成本包含运行与维护成本、投资成本、研发成本和生产成本等。由于能源品种间存在协同效应,实施两种或更多的能源比单独实施这些项目带来更多的效益(如保障供电稳定性)。经济目标要求实现电站总成本最小化,且假设只考虑两种能源间的协同效应,则经济目标函数为
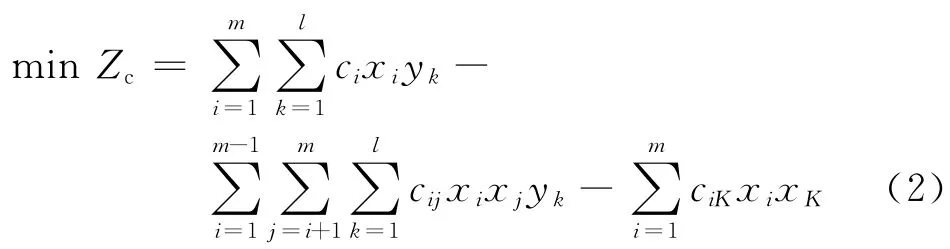
式中:i,j∈A,k∈B,K为已实施能源种类;ci、cij、ciK分别为单独实施第i种能源需要的成本,同时实施第i、j种能源减少的成本(考虑备选能源品种之间协同效用下能够减少的成本),同时实施第i种能源与已实施的第K种能源减少的成本(考虑与已实施能源品种之间协同效应下能够减少的成本,这里不需考虑选址问题,只需匹配能源品种即可),且ci,cij,ciK≥0。
实测距离采用商用精度为1 mm的激光测距仪定标,图7(a)为实际采样到的波形,前一个为激光发射波形,后一个为接收回波波形,饱和度为500%.图7 (b)中传统形心算法、窗宽自适应形心修正算法的误差频率分布分别为-3.3~-2.4 ns、0~0.7 ns,窗宽自适应形心修正算法精度有较大提升,但由于实测波形的微变形导致误差范围偏移.在饱和度50%~1 000%下计算窗宽自适应形心修正算法误差平均值Ec,并基于实测波形对偏移进行修正,即
(2)技术目标。一些项目投资失败是由于技术或管理问题造成,选用不恰当的能源资源往往会造成项目失败,进而影响选址决策。因此,技术目标可以从风险角度进行度量。风险涉及很多方面,如技术成熟度、技术效率、技术可靠性以及资源的可用性等。由于实际中对风险的确定很复杂,考虑到能源资源间的协同性,同时实施两种或多种能源会降低风险。项目风险可看成某个项目失败的可能性,即项目不能成功实施的可能性。风险目标要实现风险最小化,则风险目标函数为
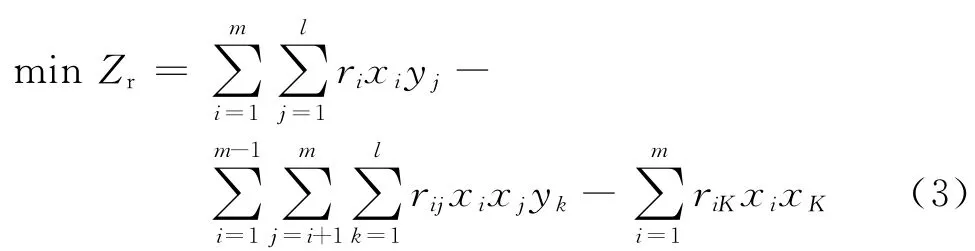
式中:i,j∈A,k∈B,K为已实施能源种类;ri、rij、riK分别为单独实施第i种能源的技术风险,同时实施第i、j种能源能降低风险(考虑备选能源品种之间协同效用下能够降低的风险),同时实施第i种能源与已实施的第K种能源降低的风险(考虑与已实施能源品种之间协同效应下能够降低的风险,这里不需考虑选址问题,只需匹配能源品种即可),且ri,rij,riK≥0。
(3)环境目标。环境目标可以从温室气体排放以及化石能源使用来度量。关联性问题与前面的目标类同,也只考虑两种能源间的关联,根据国家政策大力推进可再生能源发展,降低化石能源的比例。因此,实施多种能源可以减少温室气体排放,也会降低化石能源的使用。环境目标应实现温室气体排放和化石能源使用的最小化,则环境目标函数为
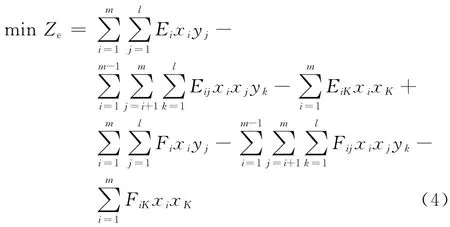
式中:i,j∈A,k∈B,K为已实施能源种类;Ei、Fi分别为单独实施第i种能源的温室气体排放和化石能源使用量;Eij、Fij分别为同时实施第i、j种能源能减少温室气体排放和化石能源使用(考虑备选能源品种之间协同效用下能够减少温室气体排放和化石能源使用);EiK、FiK分别为同时实施第i种能源与已实施的第K种能源减少温室气体排放和化石能源使用(考虑与已实施能源品种之间协同效应下能够减少温室气体排放和化石能源使用,这里不需考虑选址问题,只需匹配能源品种即可),且Ei,Fi,Eij,Fij,EiK,FiK≥0。
(4)社会目标。社会目标主要从社会接受度和创造的就业机会两方面进行衡量。社会接受度是指能源使用过程中受到公众的认可度,主要包括成本、噪声、温室气体排放、土地和水资源的使用等因素,一般而言,多种能源的综合使用会受到公众的欢迎,因此也需要考虑协同效应。就业是由能源基础设施建设后所能创造的工作机会,由于多种能源协同时会共享部分人员反而会减少新的工作岗位,但与已实施项目协同则会创造新的岗位。对于社会目标是追求最大化,其具体函数形式为

式中:i,j∈A,k∈B,K为已实施能源种类;πi、Ji分别为单独实施第i种能源的社会接受度和创造的就业机会;πij、Jij分别为同时实施第i、j种能源能提高的社会接受度和减少就业机会(考虑备选能源品种之间协同效用下能够提高的社会接受度和减少就业机会);πiK、JiK分别为同时实施第i种能源与已实施的第K种能源提高的社会接受度和就业机会(考虑与已实施能源品种之间协同效应下能够提高的社会接受度和就业机会,这里不需考虑选址问题,只需匹配能源品种即可),且πi,Ji,πij,Jij,πiK,JiK≥0。
3.2.2考虑技术异质性和互补性的约束分析

式中:i,j∈A,k∈B,K为已实施能源种类;分别为单独实施第i种能源需要的土地使用量,同时实施第i、j种能源减少的土地使用量(考虑备选能源品种之间协同效用下能够减少的土地使用量),同时实施第i种能源与已实施的第K种能源减少的土地(考虑与已实施能源品种之间协同效应下能够减少的土地使用量,这里不需考虑选址问题,只需匹配能源品种即可),且是总的可用土地。
(2)偶然性约束。偶然性约束是保证有关联项目能被选择而设定的系统约束。A j、Qj是A的一个子集,即A j⊂{1,2,…,m},Qj⊂{1,2,…,m}。偶然性约束分为两种形式:①严格互补约束,即项目间是紧密相关,要实施项目j时,要求同时实施Aj中的所有项目,即这些项目要求同时上或同时不上;②从属关系约束,即项目j本身有可能被选中,但在实施中却有条件的依赖于Qj中至少有一个项目的实施。
偶然性约束形式①为
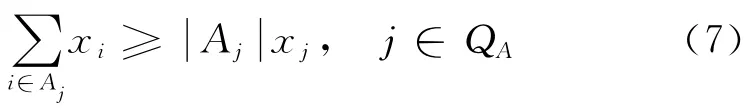
偶然性约束形式②为

式中,QO为集合{1,2,…,m}的子集。
(3)强制性约束。在能源资源开发利用中,由于法律、企业组织的政策或环境等条件所规定要实施的项目,可将已实施的项目也视为这类。强制性约束形式为:
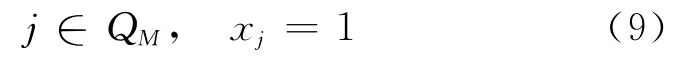
式中,QM⊂A。
(4)项目互斥约束。在项目集E⊂A,最多只能选择其中一个项目i,则互斥约束形式为

综上所述,在设定目标预期值时,应与当地的实际情况相结合,尤其是经济发展水平、资源禀赋、地形地貌以及社会习俗和文化等,还需要同时考虑国家政策法规和行业规范等约束条件,这样才能使得决策方案有效可行。
4 模型的应用
设定能源技术只有风电和光电两种,并有3个备选地址。具体背景数据为:结合文献[27-28]以及ANP的计算方法,可以计算出能源基础设施选址准则的权重,如表1所示;选址准则取值如表2所示;各地对能源的社会可接受度及备选地址的距离如表3所示。

表1 选址准则及其重要性

表2 选址准则取值
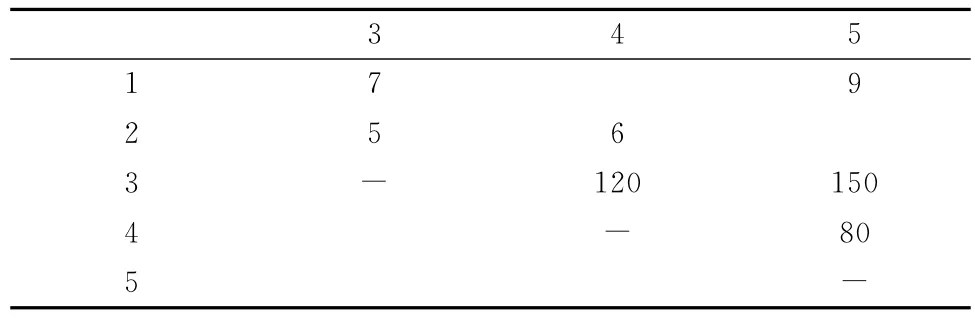
表3 备选能源的社会可接受度及地址距离
由此可得该应用例子的结构,如图5所示。
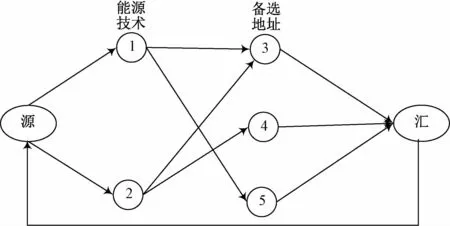
图5 算例中能源基础设施选址结构
结合模型中的目标及约束的分析,尤其考虑到协同效应,进而设定七大目标的理想值作为本文的优化目标,分别为:发电量不少于65 MW,越高越好;投资成本不得超过4 000 万/a,越低越好;年CO2减排量不少11×106t,越多越好;工作岗位增加超过25,越多越好;运行和维护成本不能超过100万元/a,越低越好;电站覆盖距离尽量超过600 km,越远越好;社会可接受度越接近最高水平18越好。
将数值代入式(1),利用Lingo软件可以得到结果,如表4所示。

表4 算例选址结果
由表4可以看出,发电量以及年CO2减排量均比预期结果要好,结果相对满意,该模型用于能源基础设施选址分析是有效的。由于算例中只考虑两种能源技术,备选地址也只有3个,故问题显得简单,所得结果有一定局限性,难以很好地反映能源技术的互补性以及协同效应。
5 结语
我国可持续能源发展战略是贯彻开发和节约并重的方针,改善能源结构与布局,能源工业的发展以煤炭为基础,以电力为中心,大力发展水电,积极开发石油、天然气,适当发展核电,因地制宜地开发新能源和可再生能源,依靠科技进步提高能源效率,合理利用能源,减少环境污染。由此可见,能源品种具有多样性,在空间分布上存在不均匀性,在进行能源基础设施投资与选址决策时需要关注能源品种间的空间与技术异质性,也要关注资源间的互补性以及项目的关联性。基于此,本文指出,在有限资源成本和一定的风险之下进行能源基础设施选址决策时,不仅需要考虑各备选项目之间的关联因素,而且要考虑备选项目与已实施项目之间的关联因素,这样才能使企业正确决策,从而获得最大利润。本文利用ANP方法分析了能源基础设施项目的关联性,进而,构建了多重选择目标规划模型,为企业进行能源基础设施投资及选址决策时提供了一种有效的方法,解决企业实施项目的多个目标及资源优化问题。在未来的研究中需要考虑更多的空间因素,结合GIS等技术收集相关数据展开深入分析,还需研究时序相关、设施相关等内容。
————不可再生能源

