基于BPSO降维的软件故障倾向模块DNN预测
刘继华,王丰锦,孔 洁
(1.吕梁学院 计算机科学与技术系,山西 吕梁 033000;2.北京航空航天大学 计算机学院,北京 100191; 3.清华同方股份有限公司,北京 100083;4.北京电子科技技术职业学院 电信工程学院,北京 100176)
0 引 言
早期的软件故障倾向性[1-3]预测方法是基于统计的,当前引入了机器学习技术,包括数据挖掘、朴素贝叶斯算法、支持向量机、深度神经网络和模糊逻辑等。虽然使用这些技术对软件故障进行了研究,但对故障数据集进行处理时,缺少对数据的降维预处理,导致算法的计算复杂性过高[4,5]。软件工程中最常用的降维方法是主成分分析(PCA)方法。例如,文献[6]在利用PCA方法对软件故障数据进行降维基础上,设计了一种两阶段的故障预测技术等。然而,PCA的一个缺点是,与原始输入变量相反,派生维度可能没有直观的解释。另一种常用降维方法是偏最小二乘法(PLS)。文献[7]利用最小二乘算法对软件故障数据进行降维,并提出一种基于时序的故障检测与故障排除的软件可靠性模型。文献[8]利用最小二乘算法对软件故障数据进行降维,并对复杂软件系统故障分布单元进行统计分析等。PLS在降维领域得到了广泛应用,但PLS的实现过程是基于非线性迭代的,通常需对原始样本数据进行假设或转换,以便使用传统的估计方法。在实际情况下,原始样本数据可能受到操作环境、测试策略和资源分配等多方面因素的影响。因此,在实际问题中很难满足这些假设。
与传统算法相比,本文创新点在于:①对于软件故障数据,引入了粒子群数据降维算法,提高数据的执行效率,并且受到测试过程影响更小;②为提高数据降维效果,提出一种束缚态粒子群算法,取代传统的粒子群算法,利用波函数代替原始粒子群算法的位置和速度,提高了数据降维效果。
1 模型方法与软件指标
1.1 模型方法
DNN[9]是基于在输出和输入两级网络层之间加入多个隐藏的网络学习单元而形成的学习算法结构。隐层在节点规模上要少于编码器输入层和解码器输出层。为对DNNs网络进行训练,引入二阶优化方法,从而实现深度神经网络训练。深度神经网络结构如图1(a)所示。
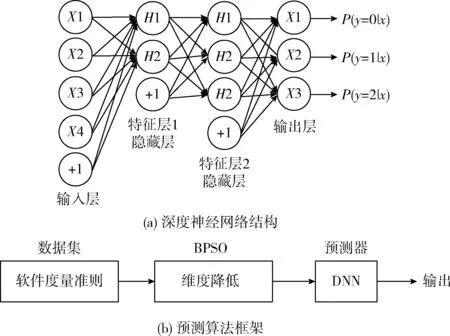
图1 DNN结构和算法框架
本文使用的是双隐层网络的深度神经网络。将场理论引入到传统粒子群优化算法,该算法是可实现全局收敛性保证的搜索方法。因此,利用BPSO算法进行算法降维处理。采用混合深度神经网络和粒子群算法,本文提出了一种有效的软件缺陷预测方法。预测方法如图1(b)算法框架所示。
1.2 软件度量指标
目前的研究大多使用软件指标来识别故障倾向性模块,研究表明软件指标对于预测故障倾向类是非常有用的。在本文中,使用的指标是McCabe,Butler,Halstead准则等[10,11]。选择的指标有代码行,循环复杂度,基本复杂度、设计复杂度等。表1列出了这些指标的描述。在本文的实验中,每个软件模块由21个指标软件故障进行倾向性表示。

表1 选取的指标
1.3 预处理过程
对于DNN算法,给定一个数据集(x(i),y(i))(i=1,2,…,q),其中x(i)∈Rd,是软件指标值的向量,它量化了第i类的指标值,q是数据样本的总数。输出神经元的第i类期望的输出值是y(i),其值为“1”对应的断点倾向和“0”对应的非断点倾向性。在训练深度神经网络时,将每个输入归一化化为相同的区间数。这有助于改善培训过程的行为,确保每个初始输入同等重要。我们注意到,软件指标的上界通常在其取值范围内是无限的。为了规范化,需要获得软件指标值范围的上下界。对于特定的数据集和软件指标,我们可以根据数据集获得每个指标的值。在这些数据集中,给出了每个指标的值,因此很容易获得最大值和最小值。
在本文中,对于每一个软件指标,令min(x(j))和max(x(j))分别为数据集的最小和最大软件指标值。然后可得尺度参数X(j)为
(1)
因此,每个记录的值被映射到封闭的区间0,1。利用(X(i),y(i))(i=1,2,…,q)规范化数据集,归一化指标向量为X(i)∈Rd。
2 基于BPSO的降维处理
2.1 粒子群优化算法
粒子群算法每个粒子根据自己和邻居节点的飞行经验,不时地调整搜索空间中的位置。它是以随机方式进行种群的初始化,该算法搜索满足某些性能的最优解。潜在的解决方案称为粒子,通过多维搜索空间飞行,如图2所示。
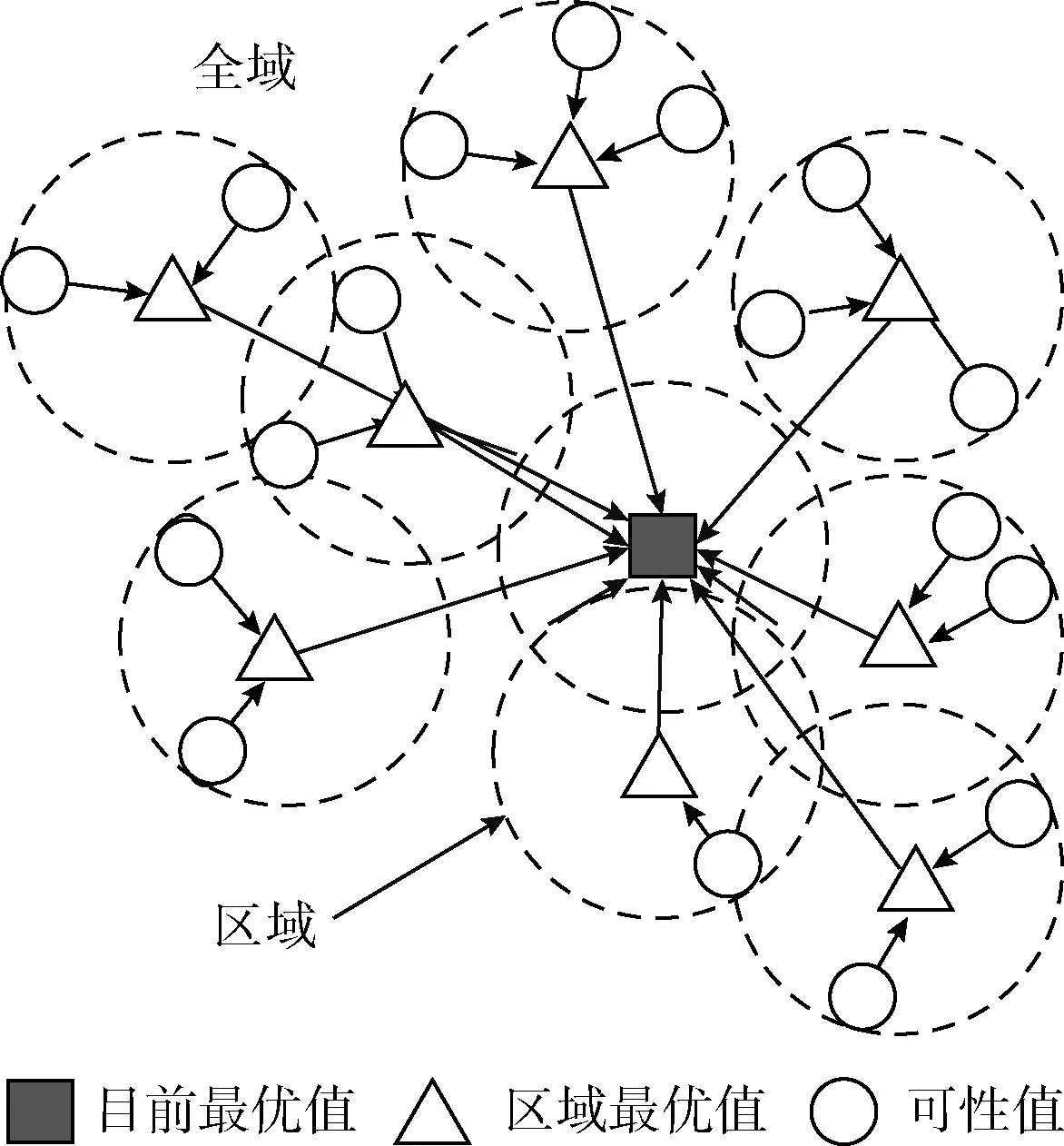
图2 粒子寻优过程
每个粒子i都有一个位置向量表示的位置Xi。用矢量表示的每个粒子的速度Vi。给出了质点速度和位置方程形式
Vi(t+1)=wVi(t)+c1r1(Pi,best(t)-Xi(t))+
c2r2(Pglobal(t)-Xi(t))
(2)
(3)
其中,t是当前迭代次数,w是惯性权重,c1和c2是正常数,r1和r2是区间0,1内均匀分布的随机数。Pi, best和Pglobal分别是当期访问粒子i的最佳位置和所有粒子位置值的最佳值,其中
(4)
式(2)中,w、c1和c2是预定义的。在迭代次数为t时,粒子i的成本值如下
(5)
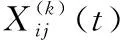

(6)
当粒子找到比先前最佳位置更好的位置时,它将被存储在存储器中。该算法将持续进行直到找到一个满意解决方案或迭代最大数量可满足。
2.2 束缚态粒子群算法

(7)
其中,参数α具有均匀特性,为膨胀收缩参数,ui、s是处于区间0,1范围内的均匀随机数,且有
pi(t)=φi(t)·Pi,best(t)+(1-φi(t))·Pglobal(t)
(8)
(9)
其中,φi是区间0,1内的均匀分布的随机数,Q是所有粒子的个数,mi, best定义为种群中所有粒子的最佳位置的平均值。粒子群算法的终止准则是,如果Ct+1和C(t)之间的绝对差异连续10次小于δ,然后停止算法;否则直到最大迭代次数Gmax可满足,其中δ是训练阈值。BPSO算法的流程如下所示:
算法1:BPSO算法
初始化所有粒子的位置和Pi,best位置。
Do
利用式(9)计算粒子i的mi, best,i=1,2,…,Q;
选择合适的值α
For 粒子i=1:Q
根据方程(5)计算粒子i的成本值;
根据方程(6)更新Pi,best;
利用以下步骤更新Pglobal;
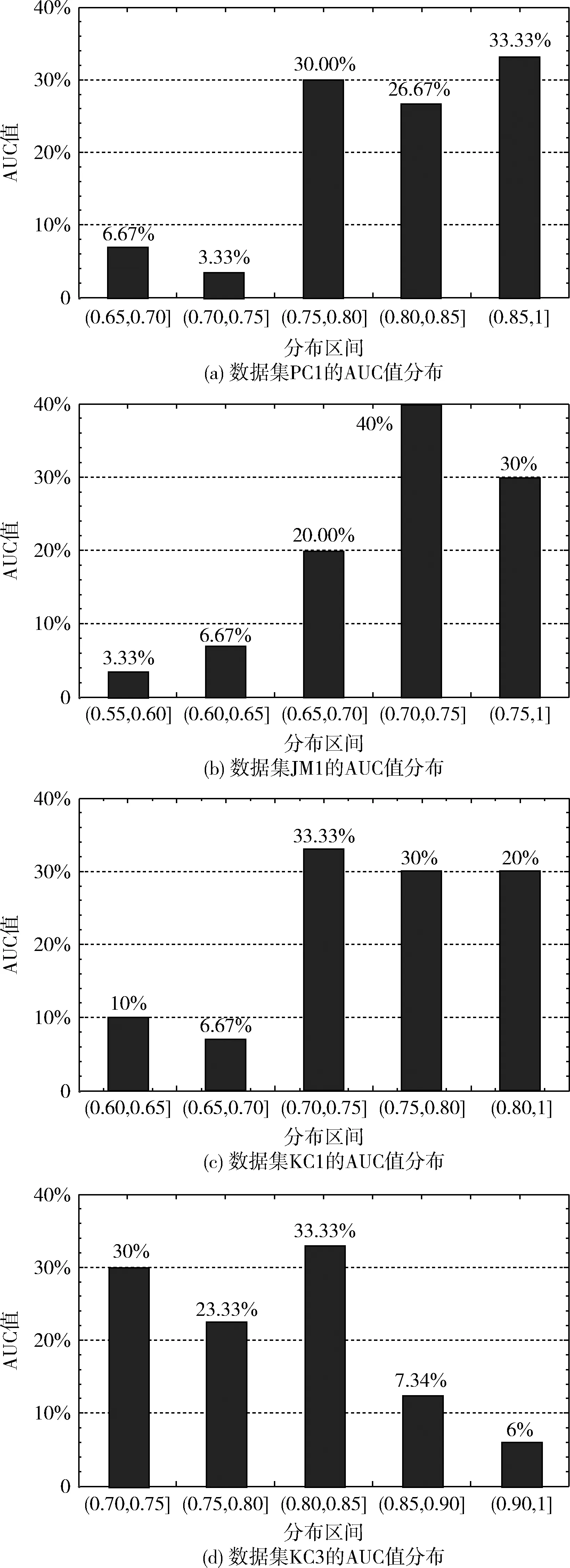
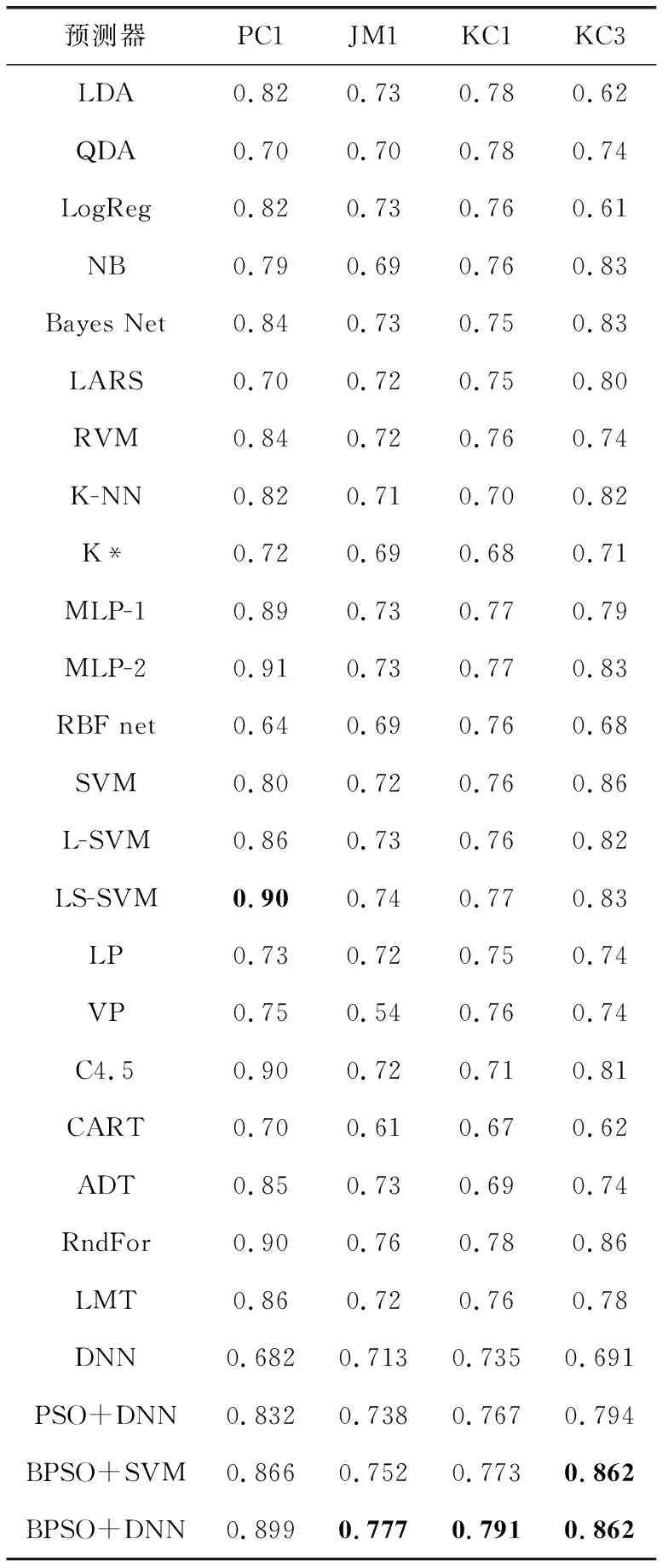
IfC(Pi,best(t)) Pglobal(t)=Pi,best(t); Else Pglobal(t)=Pi,best(t-1); Endif Endfor For 维度1:ddo φ=rand0,1; u=rand0,1; Ifrand0,1≥0.5 do 根据方程(7)上式更新粒子位置; Else 根据方程(7)下式更新粒子位置; Endfor 直到满足终止条件 假设D=(S,M)是一个带有q样本和d指标的数据集,其中M={m1,m2,…,md},S={S1,S2,…,Sq}分别是指标和样本集。C={c1,c2,…,ct}指的是类型集。为实现算法降维,我们按照以下操作将解X编码成二进制字符串 f(rand (10) 其中,S·是sigmoid函数,形式为 S(x)=1/(1+e-x) (11) 在所提降维方法中,粒子i的位置用二进制(0或1)字符串表示,例如Xi=Xi1,Xi2,…,Xid。1代表一个选定的指标,而0则表示非选定的指标。在BPSO算法中,一旦确定了最终解决方案Pglobal,最佳粒子的指标Pglobal可以跟踪其位置。我们让选定的指标集为M1⊂M,则所选择的指标值数量是l 对于所有的DNN模型,将其所有的输入数据和预期的输出进行归一化处理,使其值位于区间[0,1]。在软件故障倾向性预测方法中,深度神经网络可实现从数据空间到“1”或“0”二进制数据空间的映射。可设计软件故障倾向性预测算法如下: 步骤1 对输入指标x进行归一化处理,得到归一化的指标X。其取值位于区间0,1。 步骤2 将预处理的数据分为两个子集:按适当比例划分成训练和测试子集。 步骤3 在训练子集上建立深度神经网络模型,得到训练深度神经网络。 步骤4 基于BPSO算法从M得到一个降维子集M1,可获得降维输入数据集X′和简化DNN模型。 步骤5 在训练子集上建立简化的DNN模型,得到新的深度神经网络。 步骤6 在测试子集中使用新的深度神经网络预测模块(倾向性故障或非倾向性故障)。 步骤7 为了分析软件故障倾向性预测方法的性能,计算预测性能指标值并获得性能评价。 对于两类问题的预测性能,通常利用混淆矩阵中的数据进行评估,见表2。 表2 混淆矩阵 表2中,fij表示实际类i被预测为类j的数量,其中i,j∈{0,1}。预测性能指标选取如下:定量评价预测方法的敏感性和特异性。这些指标指标可基于混淆矩阵进行计算,计算形式分别为 (12) (13) 其中,敏感性称为故障检测率。它被定义为正确预测为故障倾向的类数与实际故障倾向类总数的比值。特异性也称为正确性。它被定义为正确预测非故障倾向的类数与非故障倾向预测类总数之比。 在这项研究中使用的数据集是国家航空和航天局(NASA)的4个关键软件项目[12],这些是美国宇航局IV和V设施指标数据程序,隶属于公共可访问的储存库。其中,PC1和JM1两个数据集是利用C程序语言编写的软件项目,一个模块是一个功能。其余两个数据集KC1和KC3 是利用C++和java面向对象的语言编写的软件项目,其模块对应一种算法。每个数据集都包含其软件指标和相关的独立布尔变量:故障倾向(模块是否有故障倾向)。根据标准McCabes规则,对于4个选取的数据集,v(G)>10的模块识别为故障倾向。表3给出了这些数据集的一些主要特性。 表3 数据集的特性 在本文中,需要确定几个参数: DNN的网络输出利用1、2表示两个类别,DNN输出选择最常用的方法是赢家通吃策略。DNN的逻辑函数选取sigmoid函数,计算形式为 f(x)=1/(1+exp(-x)) (14) (2)PSO和BPSO算法:在这项研究中,需要用户指定的PSO和BPSO算法的参数,见表4设定数据。 表4 PSO和BPSO算法参数 表4中,令参数w=0.45和c1=c2=2,α=0.55。支持向量机:正则化参数设置为1,核函数的带宽设置为0.5。 根据上面的定理,只要α满足不等式α 在实验中,训练集和测试集按3∶2的比例进行划分。基于上述参数,利用MATLAB 7.0深度神经网络工具箱可以得到一个训练好的深度神经网络。表5给出了在上述4个数据集上,PSO和BPSO算法独立运行40次的实验结果均值。 根据表5所示结果,基于PSO的维度降低方法,其选择指标的平均数量要多于BPSO算法。所选指标的算法可以更有效地简化网络架构。基于BPSO算法的指标选择结果见表6。 表5 不同数据集的PSO和BPSO算法性能 表6 基于BPSO算法的指标选取 根据表6结果,所选取的指标用于数据集(X′(i),y(i))的维度降低,其中i=1,2,…,q,X′(i)∈Rl,l=6,4,7和3。可得简化DNN模型。 在训练子集上训练简化深度神经网络后,可以得到新的深度神经网络。我们用MedCalcV11.2.0软件获得ROC曲线的AUC值。如图3所示,在4个数据集的测试子集上,独立运行30次获得的新DNN的AUC值最大的ROC曲线。 图3 原图2~5的曲线合成 根据图3,新DNN的所有AUC值均大于0.77,表明新深度神经网络可预测软件故障倾向模块。由于采取的是随机划分训练集和测试集,每次运行时新DNN预测结果不一定相同。为了评估新深度神经网络的预测能力和可靠性,在给定随机数后,在每次测试集上运行30次。图4(a)~图4(d)所示,分别为在PC1,JM1,KC1和KC3数据集上的AUC值分布情况。 图4 4组数据集的AUC值分布 根据图4(a)~图4(d)所示结果,我们可以观察到PC1,JM1、KCl、和KC3测试集上的AUC值分布情况,AUC值大于0.7的累计值分别为93%、70%、83.33%和100%。因此,预测结果稳定可靠。 利用4个数据集预测软件故障倾向性的实验结果很多,分别采用不同的预测方法。为了比较算法的预测性能,这里在表7中列出所提算法的AUC值及其AUC均值。 表7 4种数据集的预测结果对比 根据表7结果可知,在选取的预测算法中,BPSO+DNN算法在JM1、KC1和KC3上的AUC值最大,这表明该算法相对于其它算法具有更加优异的预测性能。对于数据集PC1,MLP-2,LS-SVM,C4.5和RndFor算法的AUC值均超过了0.90,其预测性能要优于BPSO+DNN算法,但是整体相差不大。这表明所提算法在性能上要优于选取的对比算法。具体分析如下: (1)所提BPSO+DNN算法的AUC值均超过了0.776,这表明,利用所提BPSO+DNN算法可实现对所有数据集软件故障倾向的有效预测。此外,软件度量之间存在很强的相关性,并且存在适当的软件度集,这也表明删除冗余度量有助于提高软件故障倾向模型的性能。 (2)对比DNN和BPSO+DNN两种算法,BPSO+DNN算法的AUC均值要始终高于DNN算法,这表明利用BPSO算法可以提高深度神经网络的预测性能,去除冗余的度量,因此基于BPSO的度量选择是很有必要的。 (3)通过对比PSO+DNN和BPSO+DNN算法,BPSO+DNN算法的AUC均值要明显优于PSO+DNN算法,这表明PSO和BPSO算法均可实现度量指标的有效选择,但是BPSO算法要明显优于PSO算法。同时,根据表5结果可知,BPSO算法选取的指标数量,要少于PSO算法,这表明BPSO算法相对于PSO算法更加具有计算效率。 (4)通过对比BPSO+DNN算法和BPSO+SVM算法,BPSO+DNN算法在PC1、JM1和KC1数据集上的AUC均值要明显优于BPSO+SVM算法,而在KC3数据集上的AUC均值两种算法相同。这表明了SVM算法在软件故障倾向预测上的有效性,也表明了BPSO+DNN算法的性能优势。 表8给出DNN、PSO+DNN和BPSO+DNN这3种算法在4个数据集上的平均计算时间,每种算法独立运行20次取均值。 表8 平均计算时间对比 根据表8计算结果可知,如果没有采取降维措施,而是直接应用软件缺陷预测,时间成本要高得多,这表明在降低运行时的降维效果非常显著。此外,BPSO算法的性能比PSO算法的降维效果更优,可实现计算时间的最大降低。 本文研究了混合深度神经网络和BPSO算法的应用开发软件缺陷预测方法。所提出的预测方法能够较为准确识别故障倾向性。所提出的预测方法的主要优点如下: (1)在本文中,BPSO算法是用于降低度量空间的维数,而深度神经网络用于预测软件模块的故障倾向。并验证了BPSO+DNN算法性能的有效性。 (2)所提降维算法实现简单,这是因为粒子群算法有3个控制参数,而BPSO算法只有一个,因此更容易实现算法的控制。实验结果表明,它是可能的,基于BPSO算法的降维技术可以简化网络结构,并获得更加的预测性能。 (3)从度量空间中选取的几个度量对于软件模块的故障倾向性而言,比其它非选择度量具有更显著的效果,这表明在软件开发过程中,开发人员应该更多地关注选定的度量指标,而不是所有的度量指标。 (4)提出的预测方法能够有效地预测软件故障倾向性,因此开发人员只需集中于具有故障倾向性的软件模块,从而最大限度地降低软件维护成本。2.3 降维方法
3 软件故障倾向性预测方法
3.1 算法步骤
3.2 性能评价指标

4 实验分析
4.1 测试数据集

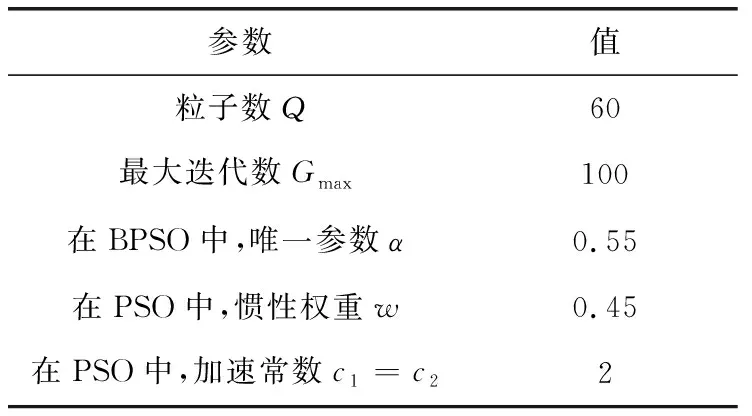
4.2 参数设置

4.3 降维和预测结果分析



4.4 算法性能对比
4.5 算法计算复杂度分析

5 结束语

