基于残差学习的CT稀疏重建伪影校正

张鹏程，谢世朋

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

0 引 言

辐射剂量问题已成为CT领域亟待解决的热点问题，当前的研究主要集中在降低电流和减少投影数方面。降低电流的方法，虽然降低了X射线的辐射量，但同时引入了较多的统计噪声。为了去除低剂量CT中的统计噪声，L.L.Chen等提出了使用改进的BM3D算法来提高图像的质量[1]，而SayedMasoud Hashemi等采用了NCRE的迭代方法减小低剂量CT中的噪声[2]。减少投影数的方法可以减少CT中的大量辐射，但同时给图像带来了严重的伪影。为了去除重建中的伪影，Shaoting Zhang等利用字典学习的方法稀疏重建[3]，张瀚铭等利用非局部的TV正则化稀疏重建[4]，张俊峰等利用伽玛正则化稀疏重建[5]，在图像去伪影方面取得了良好的效果。由于数据噪声的存在和不理想的先验惩罚项的选取，使得基于TV正则化的重建结果存在梯形伪影和片状伪影。在临床诊断过程中，片状伪影会影响到诊断的误判和正确性。其它稀疏重建的方法都需要大量的正则化约束，且恢复出来的图像有较低的PSNR(峰值信噪比)和SSIM(结构相似度)值，仍然存在较严重的伪影。卷积神经网络(CNN)已经在图像去噪、图像识别和图像分类领域取得了很好的效果且误差率都很小，在医学图像处理中得到了广泛地应用。针对这一现象，本文提出了基于残差学习的CT稀疏重建伪影校正的方法，能更好估计这些伪影的特征达到去伪影的目的。

1 方 法

本文提出了基于残差学习的CT稀疏重建伪影校正方法，首先通过FBP(滤波反投影)方法对CT产生的稀疏投影数据进行重建，重建后的图像带有严重的伪影；然后通过建立残差神经网络结构对伪影的特征进行学习，得到伪影图；最后通过稀疏重建的图与伪影的图做残差，恢复出清晰的CT图像。

1.1 FBP重建

滤波反投影重建(filtered back-projection，FBP)算法具有重建速度快、易于硬件实现等优点,当投影数据比较完备时,能快速重建出高质量图像,因此它是目前应用最为广泛的一种重建算法。对于平行束CT系统，遵循bear定律。这个投影的过程实质上是一个拉东变化的过程。探测器的距离为t，投影角度为θ，公式可以表示为

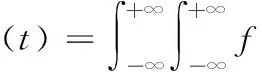
(1)

f(x,y)代表当前的图像，当t=xcosθ+ysinθ，采样投影数据充足那么FBP则有

(2)

其中，w表示斜坡滤波器，Pθ(w)表示沿着探测器方向的一维傅里叶变换，wPθ(w)就是滤波的投影。第二重积分本质上是‘滤波反投影’，即对滤波投影的数据进行傅里叶反变换，然后累积得到反投影的图像。

使用CT对患者进行不同投影数的扫描，产生60个(3600圆轨道扫描，扫描间隔为60)、90个(3600圆轨道扫描，扫描间隔为40)、120个投影(3600圆轨道扫描，扫描间隔为30)和全投影(3600圆轨道扫描，扫描间隔为10)的数据，而后对这些数据进行FBP反投影重建。由CT扫描患者肺部切片全投影成像和稀疏重建成像如图1所示。

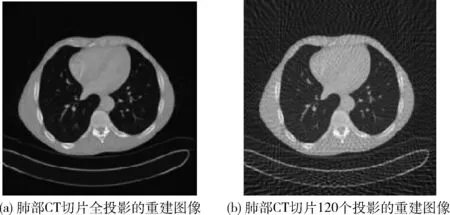
图1 全投影和稀疏投影重建

FBP稀疏重建的CT图像存在明显的条状伪影，投影数减少能够降低X射线对人体造成的辐射危害，但同时带来了伪影的增加，为了去除伪影引入了基于残差学习的卷积神经网络。

1.2 基于残差学习的卷积神经网络

由于深度学习在学习图像噪声特点方面取得了很好的效果，张凯等[6]利用残差学习卷积神经网络去高斯噪声、解决SISR和JPEG图像块效应等方面较传统的方法效果更好。另外，Yo Seob Han等[7]根据张凯的思路提出了基于残差学习的压缩感知CT重建方法，该方法在去稀疏重建伪影方面同样取得了很好的效果。基于二者的思想，本文利用基于残差学习的卷积神经网络对稀疏重建的图像进行学习，然后通过稀疏重建的图像减去学习得到的伪影图像，最后恢复出清晰的校正图像。残差学习的卷积神经网络的输入为稀疏重建图像f=x+n。在深度学习卷积网络当中，典型的去噪模型如MLP[8]和CSF[9]旨在学习一个映射函数F(f)=x预测一个清晰的图像。对于残差学习的卷积神经网络，训练的是一个映射μ(f)≈n函数。本文提出的基于残差的卷积神经网络旨在解决以下问题[8]

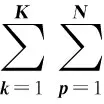
(3)

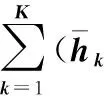
(4)

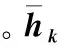
(5)

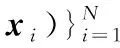
该残差学习神经网络即为本文提出的去伪影校正方法，不同于何恺明等[10]提出的用多个残差单元预测残差图像，本文只使用单个残差单元预测残差图像。由残差学习神经网络学习得到的残差图即为伪影特征图，然后根据x=f-n，得到最终清晰的图像，实现过程如图3所示。

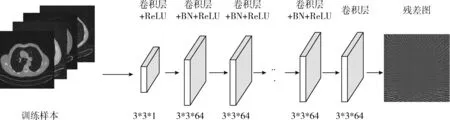
图2 残差学习卷积神经网络结构

图3 稀疏重建图中去伪影恢复CT的过程

1.2.1 残差学习卷积神经网络的具体结构

该网络的深度为D，它有3种不同的网络层，分别为：卷积网络+ReLU[11](修正线性单元)、卷积网络+批规范化(batch normalization，BN)和卷积网络层。第一层为卷积网络和ReLU构成的网络层，它由64个3*3*1的滤波器组成，用来产生64个特征映射。这一层加入ReLU，目的是在卷积网络中引入非线性，因为神经网络学习的实际数据是非线性的，卷积是一个线性操作——元素级别的矩阵相乘和相加，因此需要通过使用非线性函数ReLU来引入非线性。然而经实践证明，ReLU具备引导适度稀疏的能力，训练后的网络完全具备适度的稀疏性，而且训练后的可视化效果和传统预处理的效果很相似。正因为它有这样的作用使得ReLU的速度非常快，而且精确度很高。第二层到D-1层，在卷积网络和修正线性单元的基础上引入了BN(批规范)[12]，使用64个3*3*64的滤波器，将BN加在卷积和ReLU之间。深层神经网络在做非线性变换前激活输入值随着网络深度的加深，分布逐渐发生偏移或者变动，逐渐往非线性函数取值区间的上下限两端靠近，这导致后向传播时低层神经网络梯度的消失，进而使得深层神经网络的训练速度收敛越来越慢。BN通过一定的规范化手段，把每层神经网络中任意神经元输入值的分布强行拉回到均值为0、方差为1的标准正态分布中(即把越来越偏的分布强制拉回比较标准的分布中)，使得激活输入值落在非线性函数对输入比较敏感的区域。这样输入的小变化引起损失函数较大的变化，梯度随之变大，于是避免了梯度消失的问题，同时学习收敛速度加快，大大提高了训练速度。第三层为一个卷积层，使用3*3*64的滤波器用来重建输出结果。

1.2.2 优化加速

在训练中优化过程一般采用梯度下降法，梯度下降法有随机梯度下降法(stochastic gradient descent，SGD)和Adam算法等。其中Adam算法根据损失函数对每个参数梯度的一阶矩估计和二阶矩估计进行动态调整，使其调整到一个合适的学习速率。Adam算法在每次迭代中参数的学习步长都有一个确定的范围，不会因为很大的梯度导致学习步长的增大，参数的值也比较稳定。批量梯度下降算法的缺点是每次都会使用全部训练样本，而且每次都使用完全相同的样本集，这会使得计算相对的冗杂。相反随机梯度下降算法的实现是可以在线更新的，每次只随机选择一个样本来更新模型参数，学习速度是非常快的。在神经网络训练过程当中，SGD和Adam优化方法的引入使网络结构训练得到了更好的结果，其中Adam算法在图像高斯去噪过程中效果要强与SGD算法[7]。

2 结 果

2.1 实验数据

实验的数据由南京某医院提供，来自10个患者肺部的CT扫描。实验设备为临床使用的西门子SOMATOM Sensation 16排CT，曝光量为100 mAs，管电压为120 kVp,射线源距离探测器阵列为1040 mm，射线源到旋转中心的距离为570 mm。重建的CT图像大小为512像素×512像素，每个像素的大小为1.2 mm×1.2 mm。

设定不同的间隔扫描角度，从CT扫描中分别得获得全投影(360个投影)、120个、90个和60个投影数的原始数据，利用FBP方法对这些数据重建得到对应的重建图像。全投影重建的图像作为完整的图像，用于和稀疏投影重建的图像作对比。针对某一个投影数的重建图像，从重建的图像中随机选取400张512*512的图像作为训练数据，再从剩余中选取20张512*512的图像作为测试数据。对于残差学习卷积神经网络的输入，使用全投影图像和稀疏重建后图像之间的残差作为训练初始化值，同时对不同投影数的重建图像分别进行训练，经过20次训练后的残差图作为输出。

2.2 网络训练和参数的设定

本文为了训练的准确性而得到较好的去伪影效果，不同投影数重建的训练样本分别为400张，测试图像分别为20张，同时把网络的深度D设置为20。采用损失函数学习残差映射μ(f)估计预测残差n。优化方法选择Adam下降法，梯度的一阶矩估计α为0.01，二阶矩估计β1为0.9，β2为0.999，更新幅度的校正参数epsilon为1e-8。该残差网络的训练速率为10-3～10-4，每次训练逐渐递减。为了产生较好的去伪影效果，提取出条状伪影的特征图，训练次数设置为60。

本文在训练的过程中使用MatConvNet工具包，运行环境为MATLAB 2015a，处理器为Intel(R) Core(TM) i7_2600 CPU@ 3.4 GHz，内存为8 GB，GPU显卡为GeForce GTX 1070。在此配置环境中，通过该网络训练样本大约需要24个小时。对不同的投影数重建，通过测试程序恢复出重建的图像，所需的测试时间见表1。

表1 不同投影数经过稀疏重建恢复过程的测试时间

2.3 实验结果

2.3.1 定性分析

分别利用120个投影、90个投影和60个投影重建的图像作为样本进行训练，而后通过残差图像恢复清晰的CT图。图4显示了不同投影重建图像训练后恢复的结果，应用本文提出的方法达到了很好的去伪影效果。

图4 不同投影数重建图像经过残差学习恢复的结果

随着稀疏重建投影数的减少，仍能很好地恢复出重建的图像，效果接近全投影的原图像。使用残差网络训练方法达到了预期的处理目的了。

2.3.2 定量分析

为了验证本文提出的方法，观察图像像素强度尤为重要。本实验采用120个投影的重建图像、90个投影的重建图像和60个投影的重建图像与全投影、恢复出的图像作对比。选取全投影重建的图像与对应的不同投影个数重建的图像和恢复出的图像，测试其在同一幅CT图像中200行，120列到250列像素的强度。

图5中120个、90个和60个投影重建的图像强度偏离了全投影的像素强度，尤其是60个投影重建的图像偏离的比较严重，通过本文提出的方法恢复的图像强度已经很接近全投影的图像强度了。

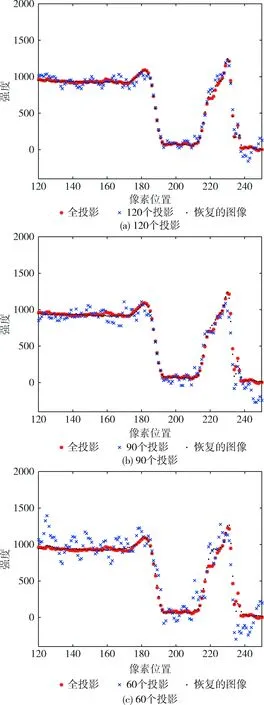
图5 全投影、不同投影个数的重建和恢复的图像(图像矩阵的第200行)在不同像素位置的强度

2.3.3 图像评价

在评价重建图像的好坏主要有两个指标：峰值信噪比(peak signal to noise ratio，PSNR)和结构相似性(structu-ral similarity，SSIM)[13]。

2.3.3.1 PSNR

PSNR的计算如下

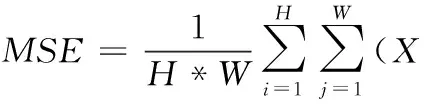
(6)

(7)

MSE表示稀疏重建图像X和通过残差学习恢复的图像Y的均方误差(mean square error)，H、W分别为图像的高度和宽度；n为像素的位深，在CT图像中位深为12。

2.3.3.2 SSIM

SSIM是一种全参考的图像质量评价指标，它分别从亮度、对比度、结构3方面度量图像相似性

SSIM(X,Y)=[l(X,Y)]α·[c(X,Y)]β·[s(X,Y)]γ

(8)

l(X,Y)为亮度对比函数，c(X,Y)为对比度对比函数，s(X,Y)为结构对比度函数，X和Y分别表示稀疏重建的图像和残差学习恢复的图像，α、β、γ是3个对比函数所占的比例因子。

本实验选取了20个原始数据作为测试数据，针对不同投影个数计算使用本文方法与全投影图像比较的平均PSNR和SSIM值，结果见表2。

表2 不同投影数稀疏重建后使用残差学习方法与全投影重建图像比较的PSNR和SSIM平均值

表2反映的是训练恢复出的图像与全投影重建后的图像峰值信噪比和结构相似度值。由上表的数据对比，随着投影数的减少重建效果在一定程度上下降了。PSNR介于20 dB～40 dB之间，效果是最佳的。当投影数太少，PSNR较小，效果要变得稍微差一些。SSIM的值也在逐渐下降。其中SSIM的值越接近于1，效果越好。

2.3.4 实验比较

为了验证本文提出方法的效果，实验部分采用了与传统方法的比较。使用张俊峰等的伽玛正则化[14]的CT稀疏重建方法分别对120个、90个和60个投影的数据进行重建，观察重建图的效果和相应的PSNR、SSIM值。图6从左到右依次是稀疏投影重建的图像、使用伽玛正则化方法重建的图像和本文提出的方法重建的图像。

从测试数据的平均PSNR和SSIM分析，可以明显的得出本文提出的方法要好于传统的伽玛正则化方法，见表3、表4。在一定程度上，利用残差学习的方法去伪影较伽玛正则化方法好。

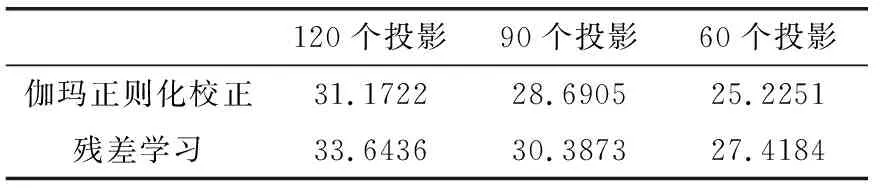
表3 不同投影数的平均PSNR/dB比较

表4 不同投影数的平均SSIM比较

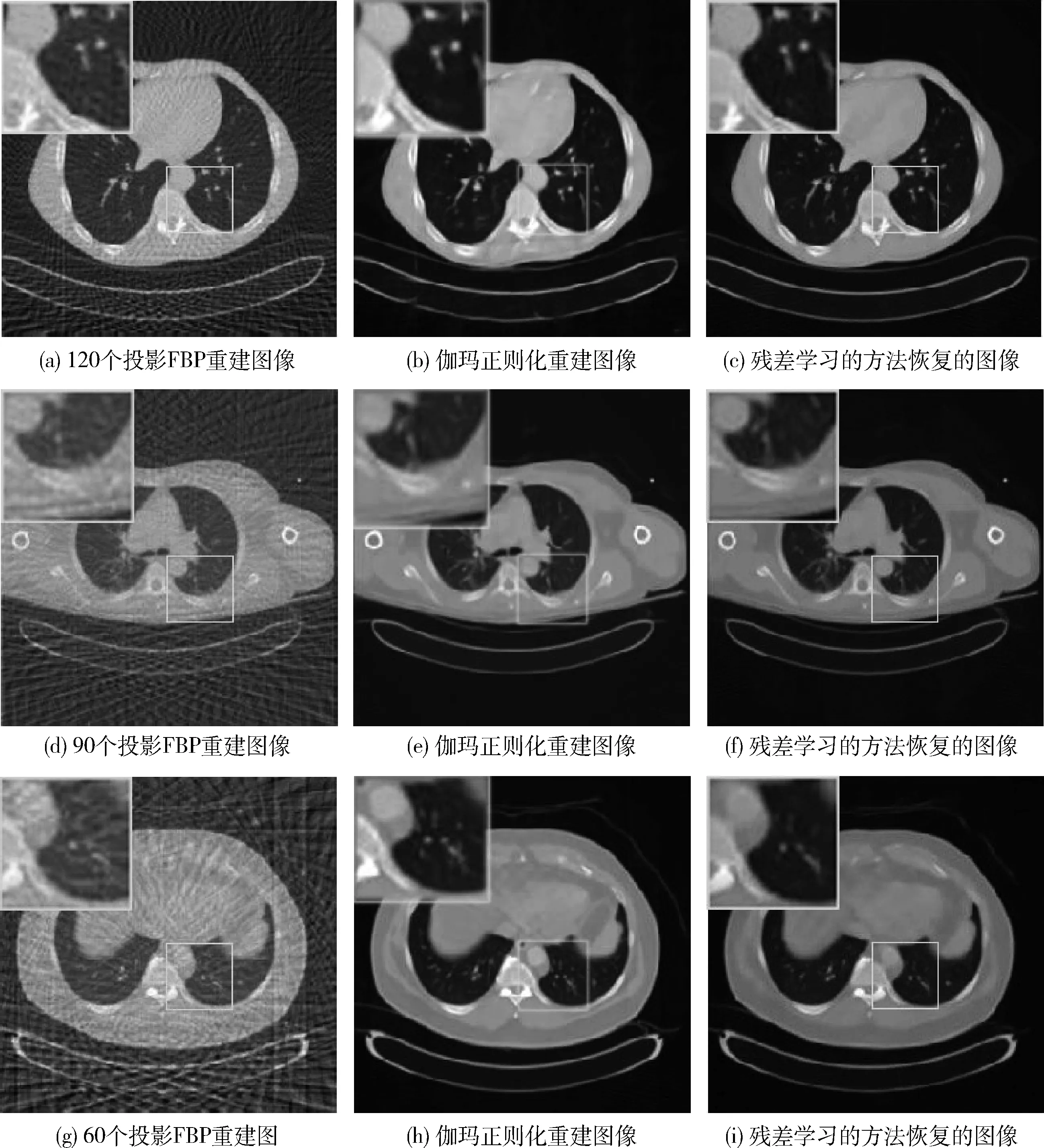
图6 伽玛正则化方法和本文方法的比较

3 结束语

与传统方法不同的是本文研究的方法在稀疏重建的基础上引入了残差学习的结构框架，在一定的程度上大大降低了X射线的辐射剂量。同时采用GPU加速，缩短了训练的时间，加速了实验的训练过程。

总之，本文提出的校正方法不需要大面积扫描人体，在现有的条件下不增加设备，不影响图像的成像质量；降低了辐射对人体不必要的伤害，达到了很好的效果。另外，该残差学习卷积神经网络结构比较单一，需要进一步优化和改进，这将是本文下一步的重点工作。