基于Spark的高维K近邻连接算法
纪佳琪,郑永基
(1.河北民族师范学院 信息中心,河北 承德 067000;2.圆光大学 计算机工学院,韩国 益山 54538)
0 引 言
K近邻连接(k nearest neighbor join),简称KNN连接,是一种简单有效的惰性数据挖掘算法[1],可广泛用于相似图像匹配[2]、相似声音匹配[3]、相似文本匹配[4]等领域。为了解决KNN连接计算量过大问题,许多学者提出了近似KNN连接算法[5,6]。然而,随着应用数据量急剧增加、数据维度不断增高,使用单机运算无法在可以接受的时间内计算出结果。为处理大规模高维度数据,使用Hadoop[7]分布式计算是一种有效的解决方案,因此很多新算法也相继提出[8-10]。文献[11]中提出了一种称为H-BNLJ的KNN连接精确算法,该算法的主要思想是首先把数据集R和S分别划分成子集,如R={R1,R2}和S={S1,S2},然后R中的每一个子集和S中的每一个子集结合形成新集合{R1S1,R1S2,R2S1,R2S2},最后发送新集合中的元素至不同的计算结点进行距离计算后再进行结果的合并,但该方法会产生大量的网络数据传输,当数据量增加或数据维度增高时,性能下降明显。文献[12]中详述了使用LSH基于Hadoop MapReduce实现的KNN连接近似算法(本文简称LSHH-KNNJ),但是MapReduce是一种批量处理的编程模型,它会把计算的中间结果存储到本地硬盘上,当需要时再从硬盘中读取,这样它的IO开销很高,因此不适合于对时间性能要求较高的应用。本文提出了一种基于Spark的使用位置敏感哈希函数[13]对数据预先进行索引的近似KNN连接算法(我们称为LSHS-KNNJ算法),并通过实验对相关讨论进行了验证。
1 背景知识
1.1 KNN连接定义
设R和S是n维空间上的两个数据集,对于任意r∈R和s∈S都是由0和1组成的n维向量。用r[i]和s[i]分别表示数据集R和S中的第i个向量,ri和si分别表示向量r和s的第i维值。设d(r,s)为向量r和s的杰卡得距离(Jaccard distance),knn(r,S)为向量r与数据集S中最近的k个向量的集合,knnJoin(R,S)表示对于每一个r∈R,返回r与数据集S中最近的k个向量的集合。具体数学定义如下:
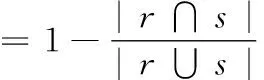
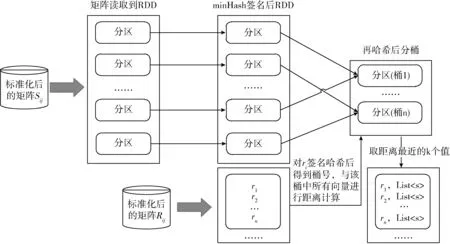
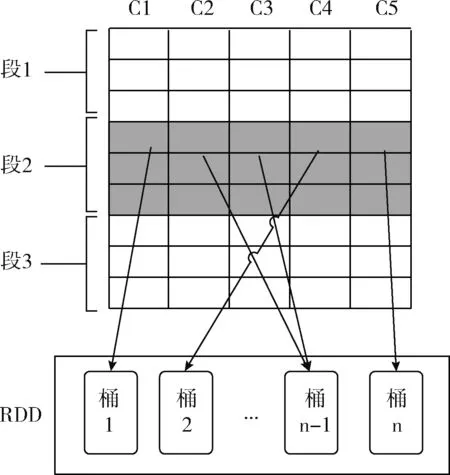
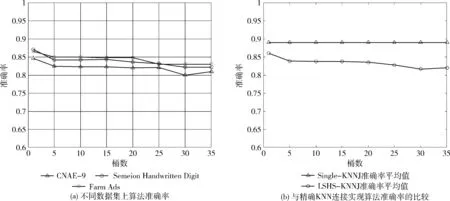
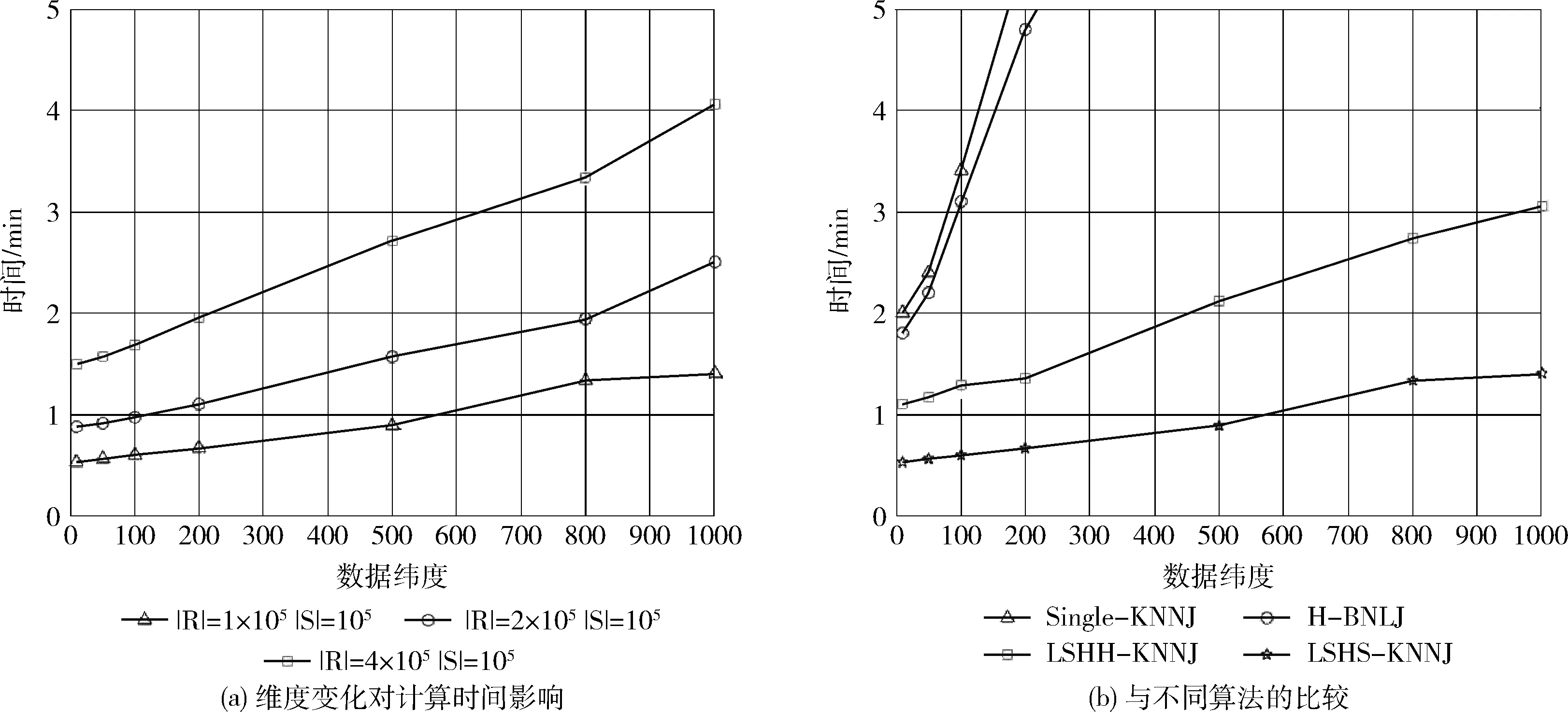
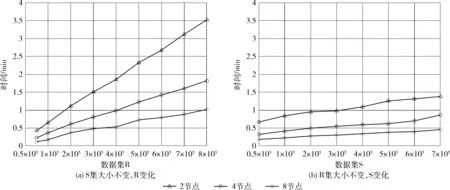
定义2knn(r,S)={(r,s[i])k|∀s[j]∈S,d(r,s[i]) 定义3knnJoin(R,S)={(r,s)|∀r∈R,∀s∈knn(r,S)}。 位置敏感哈希函数(locality-sensitive hashing,LSH)[14]是为了解决高维空间近似近邻查找的一种算法,它可以把相似的高维数据以高概率映射到同一个桶(bucket)中,因此当有新数据进行近邻查找时,只需使用相同的哈希函数把该数据映射到某一桶中,然后和该桶中的数据进行计算即可,这样可以不用遍历整个数据集进行计算。LSH定义如下: 定义4 设距离r2>r1>0,且1>P1>P2>0,Ifd(q,v)≤r1thenPH(h(q)=h(v))≥P1,Ifd(q,v)>r2thenPH(h(q)=h(v))≤P2,向量q,v称为(r1,r2,P1,P2)-敏感的。 其中,q和v是高维空间M中的任意两个由0和1组成的高维向量;由定义1知d(q,v)表示q和v的杰卡德距离。H代表若干由某一向量映射到另一向量的哈希函数,H={h:s→u};P代表碰撞概率,即映射到同一个桶的概率。 本节我们提出了在Spark上实现,基于LSH的近似KNN连接算法,我们称为LSHS KNN连接算法。该算法的主要过程如下: (1)对原始高维数据(数据集S)标准化,形成由0和1组成的高维向量矩阵Sij。 (2)对标准化后的高维向量矩阵进行minHash签名,形成签名矩阵。 (3)对签名矩阵再进行Hash映射,使相似的向量能够以高概率映射到同一个桶中。 (4)对于数据集R中的每一个向量r,使用相同的Hash函数映射到某个桶中,r与该桶中所有向量进行距离计算,并取出距离最近的k个向量返回。 上述过程都是通过Spark RDD在分布式集群中完成。图1描述了整个算法的流程,接下来将介绍一些关键步骤的具体算法和实现。 图1 LSHS-KNN算法整体流程 由于标准化后的向量仍为高维向量,在进行近邻计算时代价依然很高。为了解决高维向量计算开销过大的问题,需要找到一种方法,可以在降低其维度的同时使原有数据的特征尽可能地保留下来,这种方法就是minHash签名方法,它可以保证原始数据的相似度很高经过签名后的数据相似度依然很高,原始数据的相似度很低经过签名后数据的相似度也很低。具体算法是先对矩阵Sij进行随机行排列,则这次minHash值就是每列第一次出现1的行索引值组成的集合,重复该过程n次,即可以得到n个minHash值,即原数据的维度也变为n维。由于在具体实现的时候对Sij进行随机行排列也是一个非常耗时的过程,所以本文采用随机函数来模拟Sij进行随机排列。我们选用的随机函数为h(x)=(ax+b)/d,其中a,b是每次迭代时随机生成的正整数,x是矩阵的行索引值,d是数据的维度。其伪代码表示如下: 算法1:minHash签名 (1)初始化签名矩阵sign×d(n行,d列),值都为无穷大。 (2)随机生成a与b用于哈希函数h(x)=(ax+b)/d的计算 (3)for (r from 0 to矩阵S行数){ (4) for (c from 0 to矩阵S列数){ (5) if(S[r,c]==0) continue; (6) else对签名矩阵的每一行i=1..n计算sig(i,c)=min(sig(i,c),h(r)) (7) } (8)} (9)重复n次步骤(2)到步骤(9) 虽然经过签名后的矩阵达到了降维目的,但是当数据量很大的时候,遍历所有数据查找近邻依然极其耗时。为了解决这个问题,我们需要把相似的数据映射到同一个桶中,这样全部数据会根据相似度不同被映射到不同的桶中,当进行近邻搜索时,只需和某一桶中的数据进行计算机即可。可见,如果桶的数量是n,在数据较平均分配到桶的情况下,计算量只有原来的1/n。具体算法是: (1)把签名矩阵的若干行(具体行数可以自定义)看成一段,这样签名矩阵被分成若干段,每段有若干行。 (2)选取任意一段,对段中的列进行哈希映射(可以使用MD5或SHA等哈希算法)到桶,这样段中相同的列就会被映射到同一个桶中,这时段所在的列我们就认为是高概率相似的。 图2展示了签名矩阵哈希到桶的整个过程。接下来我们证明为什么经过该哈希过程到同一桶中后的数据是高概率相似的。假设该签名矩阵是n行m列的(由于1列代表一条数据,因此实际情况列数会很多,即列数等于数据条数;行数则是数据的维度,因此实际数值的量级在10到102),每段的行数为r,显然共有n/r段(在选取r数值时要保证n/r是整数)。假设C1列和C2列的相似度是s,则C1和C2中存在某个段相同的概率是(s)r,C1和C2在所有段都不相同的概率为(1-sr)n/r,那么C1和C2一定存在某一个段相同的概率是1-(1-sr)n/r。假设此时r=5,n=100,C1和C2相似度为s=0.9的时候,经上面的公式计算可得C1和C2一定存在某一个段相同的概率为0.999 999 982。 可见如果原数据高相似,经过哈希到桶的操作后,原相似数据有0.999 999 982的概率会被映射到同一个桶中。同理如果当C1和C2的相似度s=0.3的时候,经计算C1和C2一定存在某一个段相同的概率仅为0.0474,即原数据相似度低,则映射到同一个桶的概率也会极低。 图2 签名矩阵哈希到桶 经过上面的步骤,相当于已经对数据集S进行了索引(分桶),这时只需读取R到RDD,然后依次取出R中的元素并按上面的方法哈希后得到桶号,然后和该桶中的所有数据进行距离计算取出距离最近的k个值返回即可。算法的伪代码如下: 算法2:KNN连接查询 (1)val R_RDD = textFile(RPath) (2)R_RDD.map{ (3) 哈希得到桶号bucketNo (4) 与bucketNo桶中所有数据计算距离 (5) 返回(rid,list (6)} 为了验证算法的正确性、性能以及不同参数对运算时间的影响,我们在集群上进行了相关测试。 在物理服务器上安装了VMWare,并在VMWare中安装7台虚拟机,每台虚拟机的配置都相同,其中1台作为主结点(Master),其它6台作为从结点(Slaves),其物理服务器和虚拟机的详细配置见表1和表2。 每台虚拟机安装centos 7操作系统,Java1.8 64-bit,Hadoop 2.7.3和Spark 2.0。因为单台虚拟机最大核数是4核,所以当使用n台虚拟机时(本实验n≤8),我们设置的最大分区数应该是4n,即使超过这个值,也不会增大加速比,甚至会因为调度问题反而性能下降。 表1 物理服务器配置 表2 虚拟机配置 实验使用了3个真实的数据集:①CNAE-9 Data Set:这是一个用于文本处理的已经经过预处理的由0和1组成的数据集,有857个维度和1080条记录;②Farm Ads Data Set:是一个从12个网址收集的有关农场动物文本,标签表示该文本是否为广告,有54 877个维度和4143条记录;③Semeion Handwritten Digit Data Set:由80个人手写0-9数字,经过处理后生成16*16共256个值的矩阵(即维度是256),共1593条记录。 部分测试,我们使用由Java程序生成的不同维度不同大小符合我们数据输入标准的数据。与真实数据集比较,在测试算法的准确率时必须使用真实数据集,但是其它测试我们使用程序生成的数据集能够更加方便地进行测试且不会影响测试结果。 (1)准确率分析 该实验中我们不仅在3个真实数据集上测试LSHS-KNNJ准确率,而且还与单机精确实现KNN连接(本文简称Single-KNNJ)算法的准确率进行了比较(虽然精确实现KNN连接算法的效率最低,但是其准确率是最高的)。 LSHS-KNNJ中影响准确率的主要因素是桶的数量,从理论上分析,当桶的数量为1的时候,准确率最高,因为这等价于所有数据都映射到了同一个桶中,显然此时计算量也最大,相当于和所有降维后的数据进行计算。除此以外k值也会影响准确率,但是对于不同数据,不同应用需要不断调试来得到一个比较合理的k值,本实验中把k值固定为5。我们随机抽取数据集中10%的数据用作测试数据,其余用作训练数据,用P代表准确率,T代表测试集标签类型集合,Pr代表经KNN连接计算后的预测类型集合,则 图3(a)显示了在3个不同的真实数据集上的测试结果,结果表明无论哪个数据集都是当桶数为1的时候准确率最高,随着桶数的增加准确率略有下降,但仍然保持着比较高的准确率。 图3 准确率比较 图3(b)显示LSHS-KNNJ和Single-KNNJ在3个不同的真实数据集上准确率平均值的比较。从图中可以看出LSHS-KNNJ的准确率比Single-KNNJ略低,但差距不大。 (2)数据维度的影响 随着数据维度的增高,显然计算量会增大。但是因为本文算法最终的距离计算是和映射到某个桶中的数据进行的,因此很大程度地减少了数据维度对计算量的影响。该实验中我们使用3个计算结点,k值为3,使用程序生成数据集S和R,S集的大小固定为105,R集的大小分别取105、2*105、和4*105,数据维度取值为{10,50,100,200,500,800,1000}。从图4(a)中可以看出,当维度从10上升到1000增长了100倍时,计算时间分别仅增加了约2.627倍、2.825倍、2.699倍,可见维度对计算时间的影响非常小,因此本算法非常适用于高维数据的计算。 图4 不同数据量和维度对算法时间影响 同时,我们还与另外3个有代表性的算法进行了比较:Single-KNNJ方法,本文引言介绍的H-BNLJ方法和LSHH-KNNJ方法;从图4(b)中可以看出无论Single-KNNJ还是H-BNLJ,当维度增加时计算时间都急剧增长,无法适用于高维数据;LSHH-KNNJ虽然能够比较好地适应维度的增长,但计算时间比本文提出的LSHS-KNNJ算法约慢2倍,这主要因为本文提出的算法充分利用了Spark的高性能内存计算能力。 (3)数据量和结点数影响 随着数据量的增加,计算量因此增高,计算时间会增长;随着结点数的增加,计算时间会减少。为了更清晰地分析数据量和结点数对计算时间产生的影响,我们进行了如下实验。先保持其中一个数据集大小不变,另一个数据集大小从0.5*105到8*105变化,数据维度都为200,k=3,分别在2到8个结点上进行计算。从图5(a)中我们可以看出:①随着数据集R大小的倍数增长,计算时间增长的倍数约等于数据集R增长的倍数。显然这是因为如果R增长了m倍,计算量也会增长m倍,因此计算时间也会增长m倍;②随着结点数的增加,计算时间不断减小。结点数增加为原来的2倍,计算时间的减小始终小于2倍,这主要因为计算结点的增加会增加一部分的通信和调度的开销。从图5(b)中可以看出随着数据集S的倍数增长,计算时间增长的倍数远小于数据集S增长的倍数,这主要是因为我们对数据集S建立了索引,增加的数据按照相似度被哈希到了不同的桶中,所以实际计算量的增幅很大程度上的减少了,这也是该算法能适应大数据的一个主要原因。 图5 不同数据量不同结点数算法运行时间 本文详细介绍了基于Spark的使用位置敏感哈希函数的近似KNN连接算法。无论从理论分析还是实验结果来看该算法对高维大数据的处理是准确的、高效的,尤其是维度的变化对计算时间的影响较小使得该算法非常适用于超高维数据的场景。下一步我们将继续研究基于Spark的使用KD-Tree的近似KNN连接算法,并比较两者之间的性能差异。1.2 位置敏感哈希函数定义
2 连接算法
2.1 minHash签名
2.2 签名矩阵映射到桶
2.3 KNN连接查询
3 实 验
3.1 软硬件环境配置


3.2 数据集
3.3 测试与分析
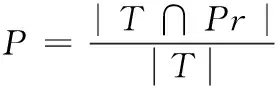
4 结束语

