基于对称矩阵的云计算和信息共享预测分类器

王 腾，高秋生，王立玮

(国网河北省电力公司信息通信分公司，河北 石家庄 050021)

0 引 言

大数据应用和研究的主要目标就是从海量大数据中提取有效信息或分析数据并预测未来发展趋势[1]。目前主要以并行计算方式进行大数据的分析，而云计算环境已经成为大数据分析常用的并行分布式计算系统。为提高云计算环境中的安全性和信息隐私，文献[2]使用异构自动复杂演化定理进行大数据挖掘，并利用Flex Analytics方法增强数据传输宽带[3]。上述两种方法都没有解决空间和时间复杂度问题，使得大数据挖掘的效率较低，无法直接应用在实际数据挖掘中。本文提出一种PSM-PBC方法，对云环境下的大数据进行计算和信息共享[4]。该方法主要包括3个过程。首先，以并行方式对分布式大数据构建三角对称矩阵，该步骤通过Householder变换可以提高云环境下数据的提取和共享速率。其次，利用交叉验证贝叶斯分类器对用户请求的实值对角数据查询结果进行评估，该步骤可以提高预测率。最后，利用贝叶斯类改进的MapReduce函数提高数据的预测分析，从而更好地计算和信息共享[5,6]。

1 基于并行对称矩阵的贝叶斯预测分类器

本文提出PSM-PBC模型用来在云计算环境中对大数据进行高效的计算和信息共享。在PSM-PBC模型中，利用三角对称矩阵更快的提取数据和信息共享，同时提高搜索精度。而交叉验证贝叶斯分类器对用户请求的结果进行评估，以提高预测率[7]。PSM-PBC模型中的MapReduce用于减少大数据的空间和计算复杂度。PSM-PBC模型如图1所示。

图1 PSM-PBC模型结构

1.1 三角对称矩阵的构造

现有的传统方法无法对用户收集的原始数据进行模式和相关性识别，而这种模式和关系在外贸企业、政府等机构的决策中有很大的帮助作用。PSM-PBC模型对分布式大数据进行并行对称矩阵运算提高数据提取的计算率。假定在云环境中并行分布有CNi个云节点，并且云节点间的计算时间由M×N矩阵形式表示，其中CTij表示云节点i和云节点j之间的计算时间[8]。根据对称矩阵的性质，有CTij=CTji，即

(1)

式中：CTi用于表示云节点i和云节点j之间的计算时间矢量V。随着数据量的快速增长，影响数据应用的因素主要是时间复杂度(如完成算法所需的时间量)和空间复杂度(如算法运行所需的存储量)。PSM-PBC模型利用对称矩阵对大数据进行实值对角搜索，并使之并行分布在整个云空间[9]。图2给出了利用Householder变换构建三角对称矩阵的过程。

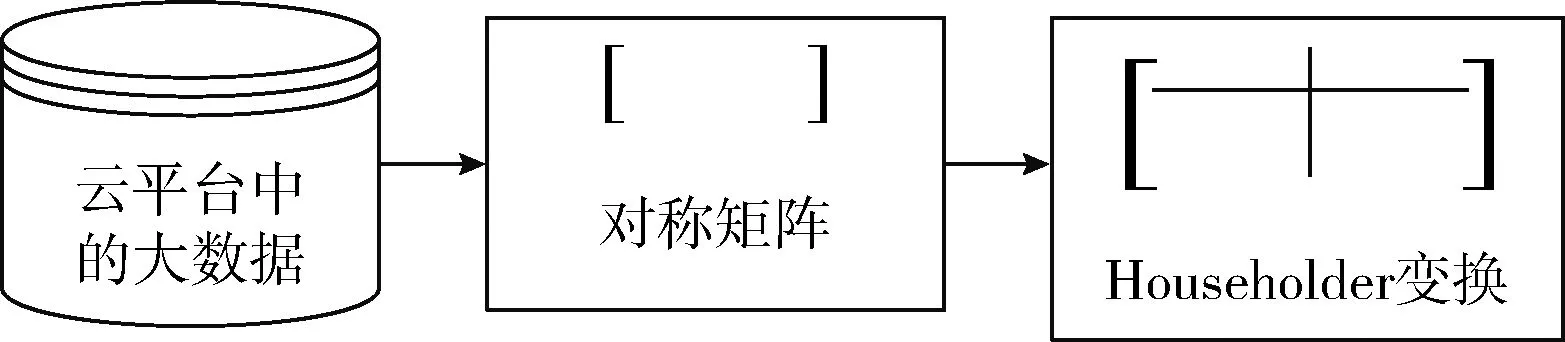
图2 三对角矩阵的构造过程

从图2可以看出Householder变换利用实值对角搜索算法将M×N矩阵变换为三对角模型。PSM-PBC模型中的Householder变换矩阵如下

HT=1-2V×VT

(2)

而HT2可以通过如下计算得到

HT2=(1-2V×VT)×(1-2V×VT)=
(1)-(4V×VT)+4V×(V×VT)×VT=
(1)-(4V×VT)+(4V×VT)=1

(3)

在PSM-PBC模型中使用Householder变换的主要目标是对大数据执行多种学习策略，提高搜索精度，并减少时间和空间复杂性。PSM-PBC模型中的矩阵对角搜索的二Householder变换的数学表述如下

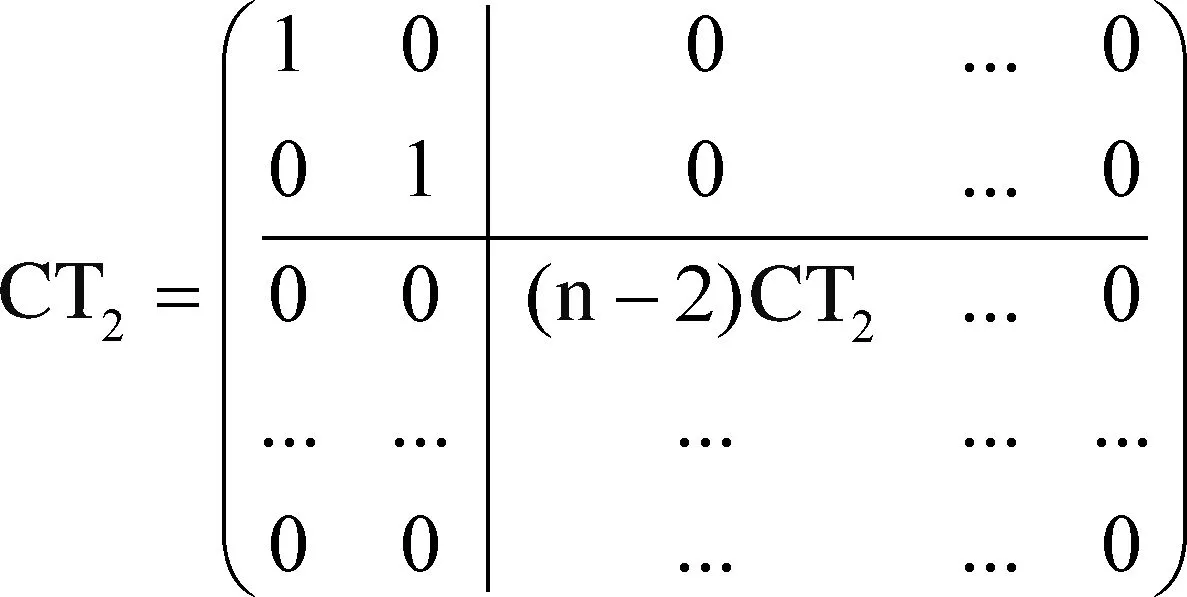
(4)

式中：左上角的单位矩阵保证了三对角化。由于Householder变换矩阵插入了一个额外的行和列，因此，通过三对角搜索可以加快分布式大数据对称矩阵的计算速度。

1.2 交叉验证贝叶斯分类器模型的设计

PSM-PBC模型中的第2步操作就是利用贝叶斯模型对用户请求进行实值对角搜索，并对结果进行有效分类[10]。假定考虑几个用户请求，那么类隶属函数或隶属函数的后验概率如下

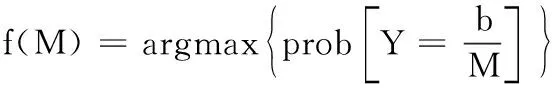
(5)

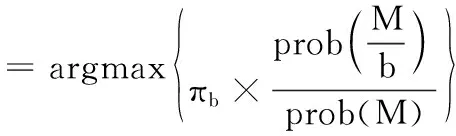
(6)

在云平台下，PSM-PBC模型在迭代“i”中选择的用户请求集由向量“vi”表示。PSM-PBC模型适用于全局和局部与云平台的交叉学习策略，用于验证贝叶斯分类器。从式(7)，选择最佳值，通过交叉验证大数据的情况下，下面的数学公式，然后进行验证

(7)

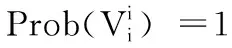
1.3 基于贝叶斯类的MapReduce函数

PSM-PBC模型最后是对MapReduce函数的应用，该方法已经用来为商业社区和政府组织提供大数据预测分析，可以实现有效的计算和信息共享[11-13]。本文中利用MapReduce函数来分析贝叶斯分类器对用户请求关键字进行分类。在PSM-PBC模型设计的最后阶段是MapReduce函数的应用。MapReduce函数法应用于从搜索数据的贝叶斯类。这种方法是由企业界和政府机构提供预测分析的大数据，并进行有效计算和信息共享化。在PSM-PBC贝叶斯类模型运用假定某些特征的存在或不存在的指示。在我们的PSM-PBC模型，贝叶斯分类fiER的百分比用户讨论分类是使用MapReduce函数。

随着数百万数量级用户的产生，由于速度和可扩展性，传统的分类技术无法应用。为了解决这一问题的空间复杂性，大数据的并行编程模型中使用的PSM-PBC模型显著提高了运算速度和降低空间复杂度。在PSM-PBC模型Map-Reduce函数以并行方式处理大数据。最初从用户请求获得的原始数据被馈送到map函数中。map函数以键值对作为输入，输出中间键值对。工作分配到一个精确的数字地图的任务是使用Apache Hadoop框架进行。

所有的云节点执行类似的计算，在地图设计中，广泛使用地方的数据，以减少空间的复杂性。成功地完成映射后，从几个云节点获得的中间结果最小化，以产生所得到的输出。该PSM-PBC模型使用Apache Hadoop框架依靠MapReduce函数和Hadoop分布式文件系统进行数据处理。

随着数据种类的增多，空间复杂度增大，传统的技术由于速度和可扩展性的落后而逐渐被遗弃。为了解决空间复杂度问题，PSM-PBC模型采用并行大数据编程模式来提高处理速度以及减少时间复杂度。对于MapReduce过程，首先将得到的用户请求数据馈送到映射函数中，映射函数使用键值对作为输入，并输出中间键值对。本文任务在Apache Hadoop框架下执行，所有云节点的映射设计都广泛采用类似计算以降低空间复杂度。然后将云节点的中间结果最小化后作为结果输出。Apache Hadoop框架就是由MapReduce函数和Hadoop分布式文件系统(HDFS)进行数据处理[13]。映射(Map)的主要目的就是将从贝叶斯类得到的类、属性和值等作为输入转换为键值对，其流程如下所示

Map(x)→(Key,Value)

(8)

(Key)→(Class,Attributes)

(9)

Map操作将训练集中的关键字进行标记，并把类和对应的关键字作为键值对输出。规约(reduce)操作把键值进行合并，最终以单键值对输出，其中键是唯一的关键字组合[14]。通过分析用户请求来分类关键字的MapReduce函数的框架，如图3所示，描述了用于分类用户请求的MapReduce函数，关键字最初被分成块。然后，对关键字块与包含用户共享文件信息的每个函数进行映射。最后文件在多个云节点进行并行处理，这比在单云节点上进行仿真实验效果更好。

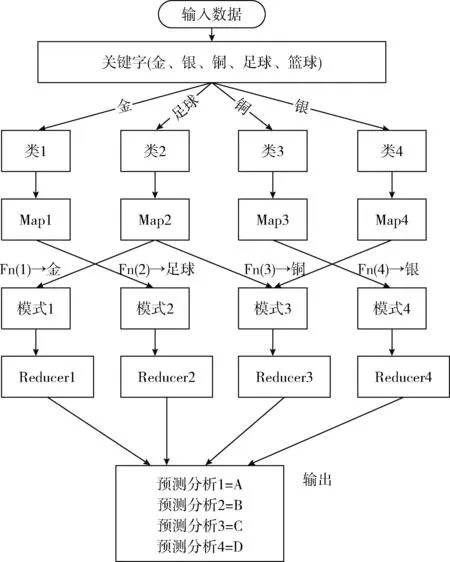
图3 MapReduce过程框架

下面给出描述了贝叶斯类的MapReduce算法的伪代码。

初始化：关键字→贝叶斯类

输出：约束功能

步骤1 Begin

步骤2 For 每类

步骤3 将该类分为n块

步骤4 将n块同时并行处理

步骤5 End for

步骤6 For 每个Map函数

步骤7 将每个Map函数分为n块

步骤8 运行Map函数

步骤9 聚合相似的类

步骤10 End for

步骤11 For 每个reducer

步骤12 结合Map函数和关键字作为输出

步骤13 End for

步骤14 End

2 结果与讨论

本文实验是在HDFS两层命名空间进行，HDFS为虚拟机实例分配不同的资源，其中每个虚拟机实例配置了特定数量的内存、CPU和本地存储器。PSM-PBC模型配有两个双核2.33-2.66 GHz Xeon处理器，7 GB RAM以及160 GB本地磁盘存储器。PSM-PBC模型使用HDFS层命名空间来降低运算的复杂度和计算成本。云计算服务首先识别出用户的请求信息共享，然后做出最佳决策的数据和信息传递给其他的用户，这样信息没有冗余。利用JAVA语言实现PSM-PBC模型，并从搜索精度、预测率、计算时间和空间复杂度4个方面进行对比研究。

2.1 搜索精度的影响

表1中对PSM-PBC方法的搜索精度做了评估同时与DM-BD[2]和FlexAnalytics[3]两个方法做了对比。为了说明实验的有效性，本文数据的大小从200 GB到1400 GB范围变化，其中，大数据的搜索精度用下式表示

(10)

式(10)中说明，大数据的搜索精度SA由正确识别模式的百分比来体现。从表1数据可以看出，搜索精度随大数据的增大而增加，且当数据大小达到800 GB时，大数据的搜索精度趋于饱和状态。

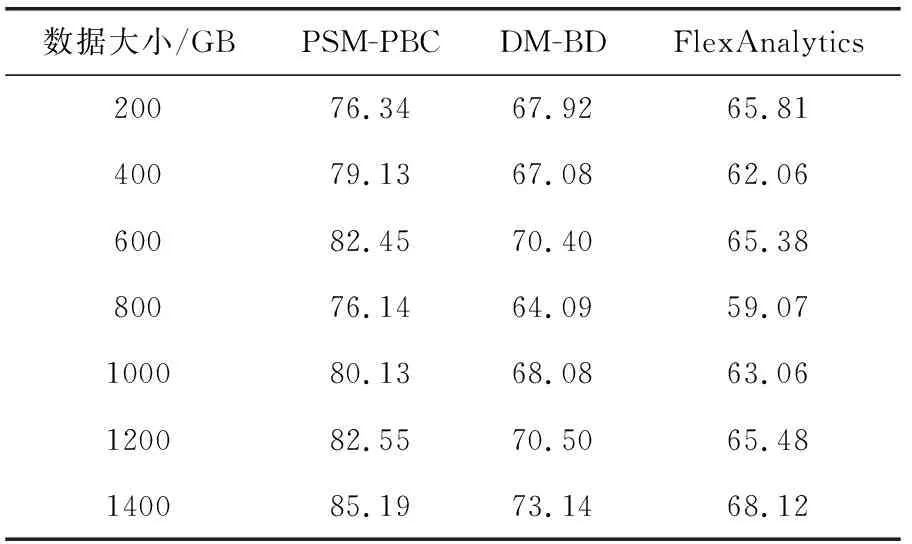
表1 搜索精度

图4相应给出了大数据搜索精度的折线表示，更直观的说明本文PSM-PBC模型优于DM-BD和FlexAnalytics方法。其主要原因是本文模型使用三对角对称矩阵识别重要模式和其相关性。相比之下，PSM-PBC搜索精度比DM-BD提高了13.42%，搜索准确率比FlexAnalytics提高了17.68%。

图4 搜索精度对比

2.2 预测率的影响

PSM-PBC模型通过考虑当前数据和历史预测用户请求来最大化预测率。所谓预测就是从现有的用户请求中提取信息，以便与其他用户分享并预测未来的结果和趋势，其数学公式如下

(11)

式(11)中，预测率PR通过结合当前数据和历史因素来体现。本实验中，数据大小从200 GB到1400 GB变化，见表2。本文对PSM-PBC的预测率同前面所提两类方法进行对比，表2数据说明PSM-PBC模型优于DM-BD和FlexAnalytics方法，主要原因是本文方法应用了交叉验证的贝叶斯分类器，可以根据用户的请求进行分类。同样地，从图5中可以看出，本文预测率相比DM-DB提高了7.27%，比FlexAnalytics提高了13.83%。

表2 预测率

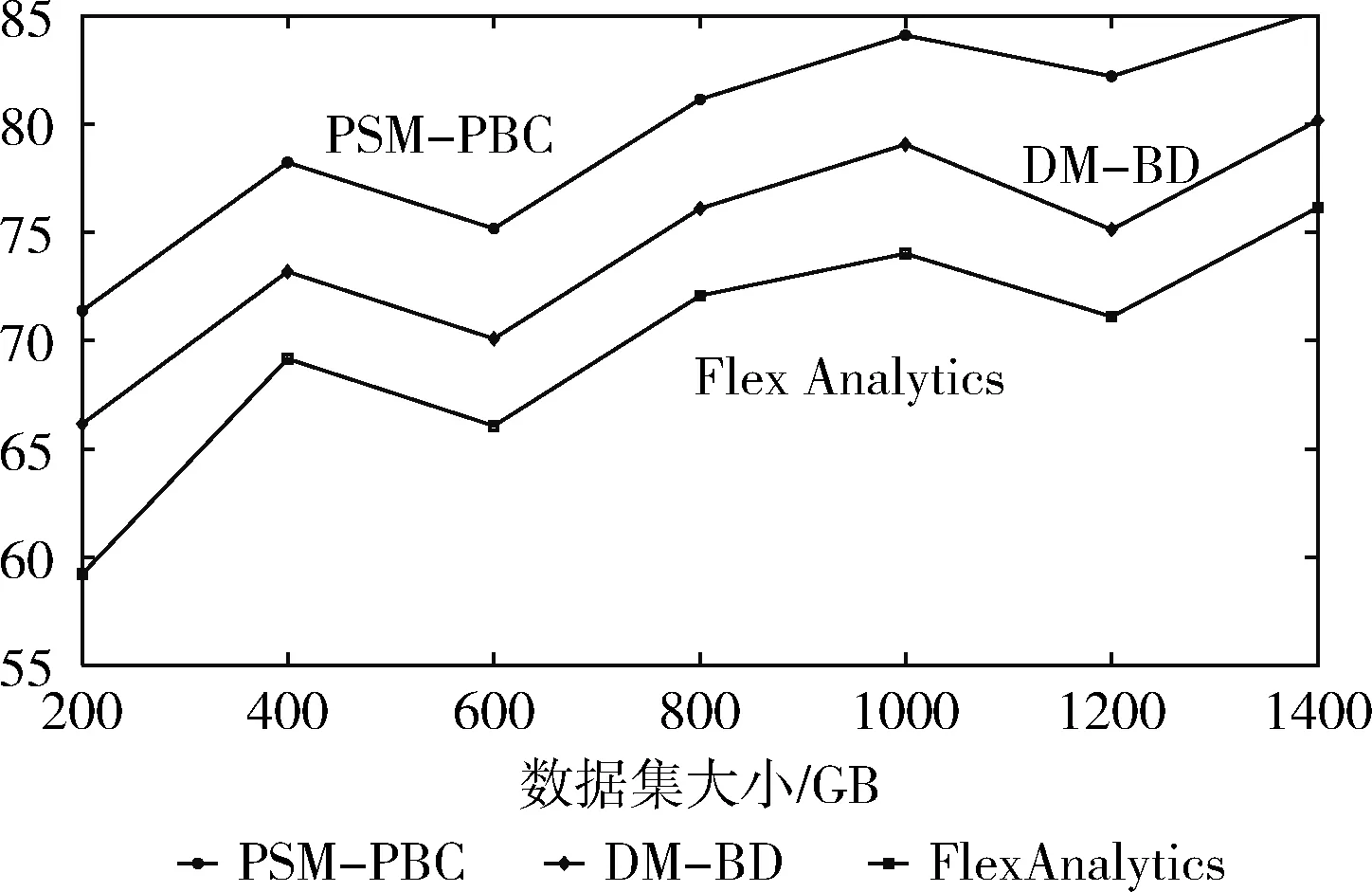
图5 预测率对比

2.3 计算时间的影响

本文所提计算时间指在云环境中构建一个有效计算和信息共享的贝叶斯MapReduce函数所需的时间，以毫秒(ms)计，数学表示如下

CT=Time(Map(n))

(12)

表3显示了计算时间与放置实例数的关系，其中实例从5到35个。从表3数据可看出，PSM-PBC的计算时间明显少。图6给出了3类方法计算时间的折线图对比。其中，PSM-PBC优于FlexAnalytics方法的主要原因是MpaReduce函数的使用。具体的，PSM-PBC比DM-BD减小了31.48%的计算时间，由于Map函数的使用，计算时间比FlexAnalystics降低了50.39%。

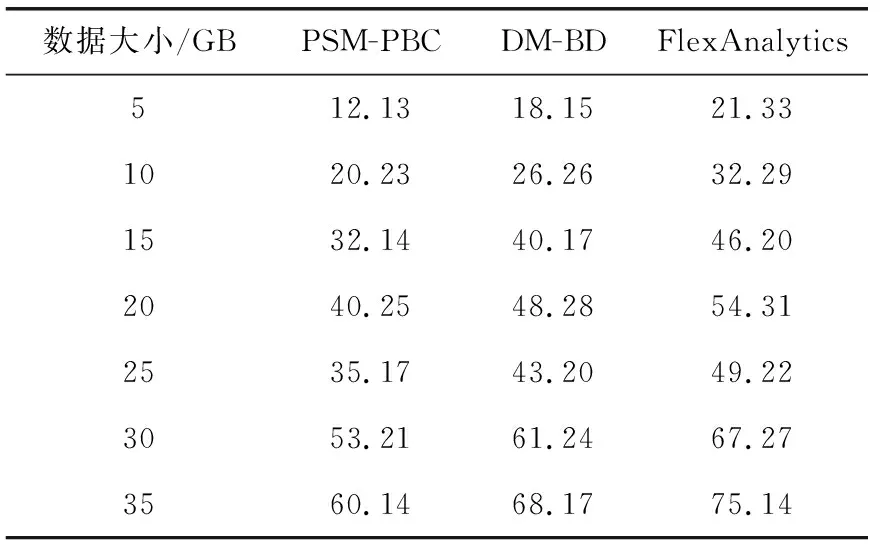
表3 计算时间

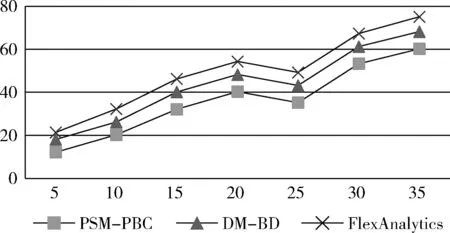
图6 时间复杂度对比

2.4 空间复杂度的影响

所谓空间复杂度指算法运行所需的内存单元数目，需要内存空间越小，说明算法就越有效。表4和图7显示了PSM-PBC模型空间复杂度的评价。本文实验采用不同数量的实例数来测量PSM-PBC的复杂度。相比DM-BD和FlexAnalystics方法，本文方法相同数量实例条件下所需空间复杂度更小。虽然3个方法的空间复杂度都随实例数的增加而增加，但PSM-PBC增加的幅度较小。具体的，使用PSM-PBC模型的空间复杂度相比DM-BD和FlexAnalytics方法分别减少了19.7%和32.5%。

表4 空间复杂度

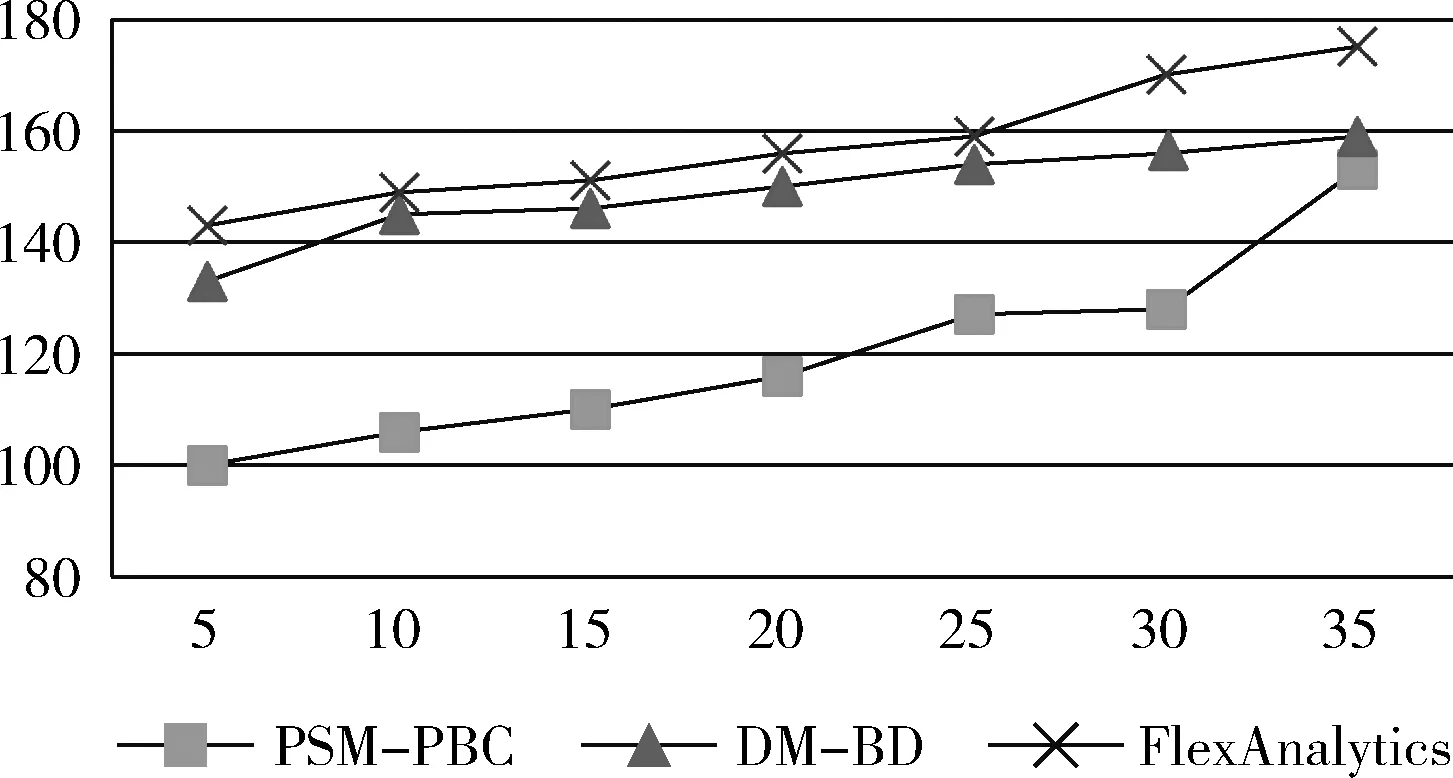
图7 空间复杂度对比

3 结束语

本文在云计算环境下提出PSM-PBC模型，旨在提高云计算环境中大数据计算和信息共享的效率。该PSM-PBC模型使用三对角对称矩阵对云环境中的分布式大数据共享，提高了大数据搜索精度。同时使用Householder变换提高大数据的搜索精度，计算时间和空间复杂度。然后，交叉验证贝叶斯分类器模型用于评估从每个用户请求获得的相应查询结果的实值对角搜索数据，从而提高了预测率。因此，该PSM-PBC模型拥有了相当好的性能，利用Householder变换和平行跨分布式云空间以提高搜索精度。然后，交叉验证的贝叶斯分类器的模型，来评估从每个用户请求获得真正价值对角线搜索数据相应的查询结果。这有助于提高预测率。本文使用国家电网大数据集进行了一系列实验，以分析搜索精度、预测率、计算时间和空间复杂性，以便测量PSM-PBC模型对大数据的有效性。相比之下，本文方法较DM-BD和FlexAnalytics效果更优。