基于两阶段流形学习的半监督维数约简算法

徐金成，李晓东，刘 辉

(1.广东司法警官职业学院 信息管理系，广东 广州 510520； 2.国家计算机网络应急技术处理协调中心广东分中心， 广东 广州 510665)

0 引 言

维数约减算法的目的是在保持数据的本质信息的前提下减少数据的复杂度。目前有大量半监督维数约简算法提及：半监督维数约减算法能够同时利用有标签和无标签训练样本进行综合考虑。

一些研究者定义新的优化目标。Jincheng Xu[1]提出了一种对称局部保持的半监督维数约减(SLPSDR)算法，该方法主要是针对自然界较多图像具有对称的特点以及数据分布大多呈一定的流行结构情况。Yi Yang等[4]提出一种排序学习的半监督维数约减算法，使用局部预测误差表示样本之间的流形结构，该方法假设的流形结构与多媒体数据有较好的一致性，但是该方法没有处理全局流形结构。Jia Wei等[3]提出一种结合局部和全局拓扑结构的半监督维数约简算法，该方法通过最小化类内距离和类间距离来突出分类结构，局部拓扑结构通过最小化局部重构误差实现，全局拓扑结构通过最大化不在邻域的样本之间的距离实现。

一些研究者定义新的流形结构。Tingjin Luo等[8]提出一种判别正交弹性投影保持方法(DOEPP)，该方法使用EPP中的方法构建局部图和全局图，使用最大间距准则中的方法提取判别信息和正交信息。Puhua Chen等[5]提出一种基于稀疏图的半监督维数约简方法，该方法首先利用邻域对无标签样本赋予伪标签，然后根据标签建立类内和类间稀疏表示图，最后使用特征分解方法得到映射矩阵。兰远东等[6]通过最小化样本到其所属类别的中心点之间的距离，得出其邻域的拓扑结构；再通过最大化不同类别边缘间的距离，在投影子空间中就可以增强类别间的分离度。王宪保等[7]提出了一种半监督等距映射算法，该方法使用训练样本的标签样本构建K连通图，得到近似样本间测地线距离，并把它作为矢量特征代替原始数据点；然后通过测地线距离计算核矩阵，用半监督正则化方法代替多维尺度分析算法处理矢量特征；最后利用正则化回归模型构建目标函数，得到低维表示的显式映射。Xianglei Xing等[9]通过融合多种局部集合信息来获得可信度更高的流形结构。ShengHuang等[10]提出一种全局局部保持的维数约简算法，该方法使用薄板样条和核径向基核拟合数据的流形结构，能够捕获到步态中动态和静态特征。

上述方法在建立数据流形结构时，直接使用高维数据。但是高维数据在样本空间非常稀疏，流形结构可能不明显，并且流形结构也容易受到噪声的影响，导致保持该流形结构对分类的意义减小。为了克服上述问题，本文提出先利用原始数据建立数据的流形结构，并在该流形结构的基础上，将训练数据映射到低维空间。然后在低维空间中，建立新的数据流形结构，并在该流形结构的基础上，得到最终的映射矩阵。显然，在低维空间建立流形结构有3个好处：①低维空间由根据整个训练数据学习到的映射矩阵获得，能够过滤掉噪声的影响；②低维空间获得时，还考虑了有标签训练数据，建立的流形结构考虑了类别结构；③在低维空间中数据维度更低，流形结构更明显。

1 算法基础

TSMSDR算法是在线性判别分析和局部嵌入的基础上研究得到，所以本节对这两种算法进行简单介绍。

1.1 线性判别分析(LDA)

(1)计算样本的类内距离Sw和类间距离Sb

(1)

(2)

其中，C为类的个数，ui为第i类样本的均值，ni为第i类样本的个数。

(2)计算Sw=λSb的特征值，并将特征值从大到小排序，选取前k个特征值对应的特征向量w1,w2,…,wk构成m×k的映射矩阵W。

(3)可使用Y=WTX将数据从高维空间映射到低维空间。

1.2 局部与全局保持的半监督维数约减(LGSSDR)

(3)

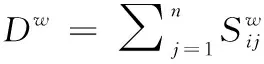
(4)

Sw定义如下

(5)

Sb定义如下

(6)

Sf定义如下

(7)

1.3 判别正交弹性投影保持方法(DOEPP)

(8)

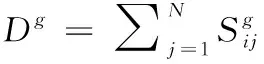
(9)

(10)

2 两阶段流形学习半监督维数约简算法(TSMSDR)

本节将给出本文提出的对称局部保持半监督维数约简算法，首先给出视觉信息处理中的对称现象及其保持方法，然后给出TSMSDR的目标函数及其优化方法，最后给出本文提出的TSMSDR算法。

2.1 TSMSDR的目标函数及其优化

(11)

其中，Lb与Lw的定义与式(3)中的Lb与Lw相同，Lg′=Dg′-Sg′,Sg′定义如下

(12)

Lm′分成两阶段定义，第一阶段Lm′的定义与式(3)中的Lm定义相同。第二阶段Lm′的定义如下

Lm′=(I-A′)T(I-A′)

(13)

其中，A′使用下式优化得到

(14)

可以看到优化式(11)是一个广义瑞利商的问题[3]，如果Lw+aLm′非奇异，那么式(11)的优化可通过求解下式的特征值和特征向量完成

X(Lb+aLg′)XTw=λ(Lw+aLm′)w

(15)

将特征值从大到小排序，选取前k个特征值对应的特征向量w1,w2,…,wK构成m×K的映射矩阵W。

2.2 TSMSDR算法

根据前面一节的描述，TSMSDR可总结成如下算法：

算法TSMSDR:

输出：映射矩阵W

(1)在输入数据的基础上。根据式(5)和式(6)计算Lb和Lw。根据式(12)计算Lg′。根据式(13)计算第一阶段的Lm′。

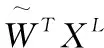
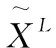
(5)使用Lb,Lw,Lg′和第二阶段的Lm′，根据式(11)计算第二阶段的映射矩阵W。

2.3 TSMSDR算法的理论依据

本小节依次分析式(11)中各个组成部分的原理与作用。

Lb,Lw的定义与式(3)中的Lb,Lw一样。其中最大化WTXLbXTW，可以最大化低维空间中类间样本之间的距离；最小化WTXLbXTW，可以最小化低维空间中同类样本之间的距离。达到使分类结构更突出的目的。

Lg′的定义根据式(10)改进而来。该式的功能与式(3)中Lf的功能相似，能够保持数据的全局流形结构。但是式(3)中Lf有一定的缺点。首先式(7)在定义Lf时样本对之间的权重相同，导致即使两个样本之间的距离非常大时，依旧有可能最大化这两个样本之间的距离。显然，使两个离得非常远的样本之间的距离离得更远意义不大。其次，式(7)在定义Lf时，只定义邻域之外的样本对之间的关系，这会导致邻域之外和邻域之内的样本之间的关系在优化时，赋予的职能会发生突然变化，影响样本之间流形结构的保持。这对本文算法的影响较大，因为本文算法需要利用第一阶段维数约减结果建立流形结构。

Lm′的计算公式与式(3)中Lm的计算公式相同，两者的差别是Lm′分成两阶段计算得到。第一阶段直接使用原始高维数据计算得到，第二阶段使用第一阶段获得的低维数据计算得到。本文使用两阶段的方法计算Lm的原因是：在大部分实际应用中，训练样本的维度经常远远大于训练样本的个数，即容易出现高维度小样本的问题。这会导致在原始高维数据上的流形结构不明显，并且容易受到噪声的影响。

使用两阶段的流形结构建立方法有如下好处：①本文使用式(12)定义一种渐变的全局流行结构定义方法，可以使第一阶段获得的低维空间中的流形结构并不会发生较大的变化，为第二阶段流行结构的建立打下了基础；②另外在第一阶段获得低维空间时，还考虑了类别结构，使第二阶段建立的流形结构中蕴含分类信息；③第二阶段建立流形结构的输入数据维度更低，可以使流形结构更加明显；④经过一次维数约简之后建立的流行结构，对数据小的变化和噪声有一定的克服能力。

3 实验结果

3.1 对比算法与实验设置

TSMSDR是一种维数约简算法，其中维数约简算法有无监督、有监督和半监督维数约简算法，所以本文将与以下算法比较：①无监督维数约简算法，包含主成分分析法(principal components analysis，PCA)；②有监督维数约简算法，局部投影保持(locality preserving projection，LPP)[2]，包含线性判别分析(linear discriminant analysis，LDA)[2]，判别正交弹性投影保持方法(discriminative orthogonal elastic preserving projections，DOEPP)[8]；③半监督维数约简算法，包含局部与全局拓扑结构保持半监督维数约简算法(local and global structures for semi-supervised dimensionality reduction，LGSSDR)[3]，边缘判别嵌入与局部保持的半监督维数约减算法(semisupervised marginal discriminant embedding and local preserving for dimensionality reduction，SSMDELPDR)[6]。其中LGSSDR，DOEPP，SSMDELPDR均需要设置平衡参数。其中LGSSDR需要设置全局保持和局部保持平衡参数，均设为0.1。DOEPP需要设置弹性保持能力平衡参数，设为0.1。SSMDELPDR需要设置边缘嵌入平衡参数，设为0.1。

一般来说维数约简的主要目的是分类，所以在维数约简后使用分类器验证各个半监督维数约简的效果。支持向量机(support vector machine，SVM)[12]是一种非常经典的分类器，并且能取得较为稳定的结果。所以本文使用SVM作为分类器。另外因为维数约简后，以及本文算法在人脸数据库上验证，在维数约简之后，各个类的训练数据均能较为密集的聚集在一起，所示SVM使用线性核函数。

验证半监督维数约简算法需要3种数据：有标签训练数据，无标签训练数据，以及测试数据。本文采用两种实验设置验证算法。第一种从每个类别中随机选择3个作为有标签训练数据，再从剩下的数据中再随机选择3个作为无标签训练数据，其它剩下的数据为测试数据。第二种从每个类别中随机选择6个作为有标签训练数据，再从剩下的数据中再随机选择3个作为无标签训练数据，其它剩下的数据为测试数据。这里使用不同的有标签训练数据的目的是为了说明本文算法对训练数据的个数不敏感。为了减小样本不一样带来实验结果的差异，以上实验重复执行50次，这50次实验的均值作为最终实验结果。另外，本文对比的大部分算法均能达到较高维度的维数约简结果，本文将维数约简之后的维度取值为20,40,60,80,100,120,140,160等，其目的是为了说明维数约简之后的卫队对对比算法的影响。实验结果使用准确度(accuracy)评价。

3.2 分类结果

为了验证TSMSDR，分别使用所有参与对比算法进行维数约简，使用SVM作为分类器，根据分类结果评价TSMSDR。先给实验策略1在4个人脸数据库上的分类结果，实验结果在表1中给出，在该实验策略中有标签训练数据从每个类别随机选取3个，无标签训练数据从每个类别剩余的数据中随机选取3个，其它数据为测试样本。从表1中可以看到，TSMSDR的实验结果比第二好的实验结果在4个数据库中分别高1.08%，1.160%，0.78%，2.33%，验证了TSMSDR的有效性。

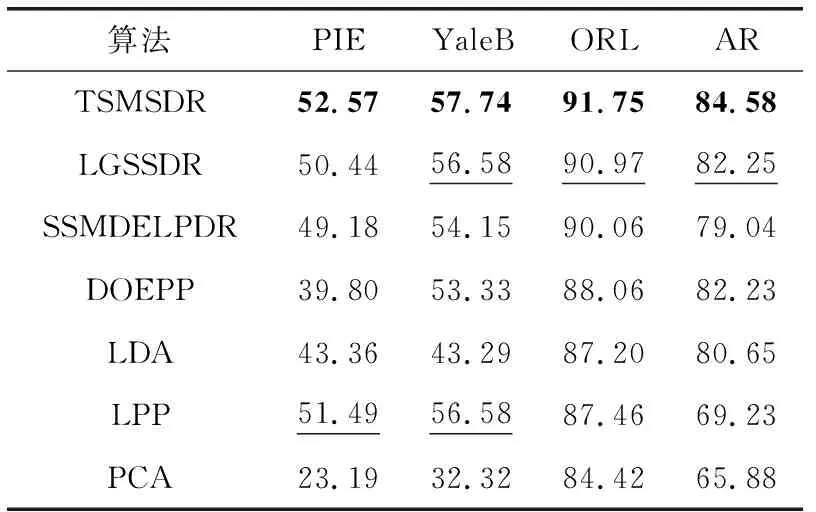
表1 所有算法在4个数据库的最大分类准确度(使用3个有标签训练样本)

另外为了对比TSMSDR与其它对比的算法投影到不同维度时的实验结果，将使用实验策略1时，所有算法在4个数据库上投影到不同维度时的准确度分别在图1到图4给出。从图1到图4可以看到，在4个数据库上，TSMSDR能在较低维度上就能达到较高的分类准确度，这在对速度要求非常高的应用环境中，可以将数据投影到更低的维度，以加快算法的执行速度。另外从图1到图4还可以看到，TSMSDR能在较多的维度上取得较为稳定的准定度，对在实际应用中选择合适的投影子空间的维度K更有利。

图1 所有算法在PIE数据库上投影到不同维度时的准确度

图3 所有算法在ORL数据库上投影到不同维度时的准确度

图4 所有算法在AR数据库上投影到不同维度时的准确度

同样，在表2中给出实验策略2在4个数据库上的实验结果，在该实验策略中有标签训练数据从每个类别随机选取6个，无标签训练数据从每个类别剩余的数据中随机选取3个，其它数据为测试样本。从表2中可以看到，TSMSDR的实验结果比第二好的实验结果在4个数据库中分别高1.27%，1.79%，0.90%，0.70%，验证了TSMSDR的有效性。

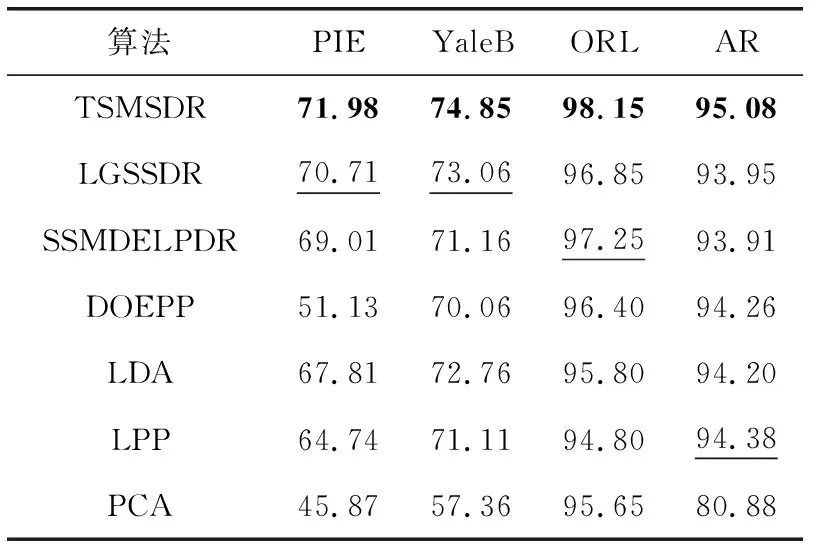
表2 对比算法在4个数据库的最大分类准确度(使用6个有标签训练样本)

同样，为了对比TSMSDR与其它对比的算法投影到不同维度时的实验结果，将使用实验策略2时，所有算法在4个数据库上投影到不同维度时的准确度分别在图5到图8给出。从图5到图8可以看到，TSMSDR能在较低维度上就能达到较高的分类准确度，能在较多的维度上取得较为稳定的准定度，以及在大部分维度上的识别均高于其它算法的识别率。

图5 所有算法在PIE数据库上投影到不同维度时的准确度

图6 所有算法在YaleB数据库上投影到不同维度时的准确度

图7 所有算法在ORL数据库上投影到不同维度时的准确度

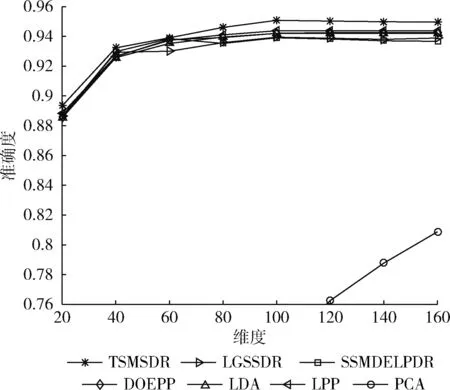
图8 所有算法在AR数据库上投影到不同维度时的准确度

4 结束语

本文算法注意到在大部分实际应用中，在原始高维数据上建立的流形结构不稳定，不突出，提出一种两阶段的流形结构建立方法。第一阶段在原始高维数据上建立流形结构，第二阶段在第一阶段获取的低维空间中建立流形结构。另外为了使第一阶段获取的低维空间流形结构不发生较大的变化，本来还使用一种新的方法建立样本的全局关系。

实验结果表明，本文算法在人脸识别上能有较好的维数约简的效果。但是，本文通过数据的全局结构保持，以减小第一阶段获得的低维空间的流形结构与原始数据的流形结构之间的差别，从而为两阶段的流形结构打下基础。该方法可能在一定程度上使第二阶段的流形结构并不完全正确。所以在将来研究一种更好的方法使建立的流形结构能够克服高维小样本的问题。