基于改进极限学习机的入口氮氧化物预测

金秀章，张少康

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引 言

人工神经网络已经被广泛的研究，但是很少应用到工业中，主要是因为神经网络需要大量的时间来进行训练，不能满足工业上的需求[1]。极限学习机(ELM)具有学习速度快、泛化能力强的特点[2]，并被许多学者研究。将递推思想引入ELM中，提出了在线贯序极限学习机[3](OS-ELM)。

OS-ELM算法认为新旧训练数据的权重是相同的，对于时变系统而言，预测的效果并不理想[4]。虽然加入l2-正则化的算法可以降低对隐含层节点的依赖程度，但是仍然不能有效确定节点数，隐含层节点的多少会对预测产生很大的影响，节点较少不能完全表达数据信息[5]，节点过多可能出现过拟合的情况，降低预测的精度[6]。

基于上述问题，提出了一种基于自适应遗忘因子和灵敏度剪枝的极限学习机(SAFFOS-RELM)，自适应遗忘因子可以根据每次新到的数据进行更新，灵敏度剪枝算法可以优化初始的网络结构，在保证预测精度的条件下得到最优的隐含层节点数，减小计算的时间，将此算法应用到Mackey-Glass混沌时间序列和脱硝系统的入口氮氧化物时间序列中，并和OS-RELM、FFOS-RELM算法进行了对比，准确性和泛化能力得到了提高。

1 OS-ELM算法

OS-ELM的SLFN回归模型为

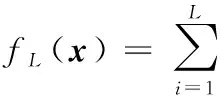
(1)

式中：g(·)为激活函数，ai和bi为隐层的参数，βi为隐含层第i个节点到输出层之间的权值，L为隐层节点数。

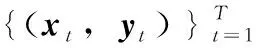
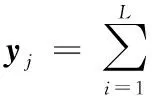
(2)

将式(2)改为矩阵形式，如下所示

Hβ=y

(3)

式中

(4)

(5)

贯序更新阶段只对输出权重β进行更新，矩阵H中的参数是随机得到的，输出权重的公式如下

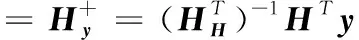
(6)

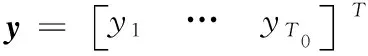
通过对式(6)的推导可以得OS-ELM算法的步骤如下：

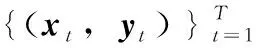
1)建立一个初始训练数据D0。

2)选取激活函数g(·)，随机产生隐含层参数ai和bi，i=1,2,…,L。

3)根据式(4)计算H0。

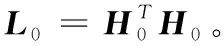
5)令k=0。

(2)贯序更新阶段：

1)根据式(4)和第k+1次的数据得到Hk+1。

2)根据下式计算每次的输出权值公式

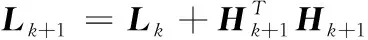
3)令k=k+1，返回(2)中的步骤1)继续执行。

2 SAFFOS-RELM算法

2.1 FFOS-RELM算法

OS-ELM中加入l2-正则化方法避免矩阵HTH出现奇异的情况，降低网络预测误差。加入l2-正则化方法[9]，转化为以下寻优问题

(7)

式中：C为正则化系数，对式(7)求解可以得出

β=(HTH+I/C)-1HTy

(8)

则FFOS-RELM算法的递推公式如下：

根据式(8)可知，初始的输出权重为

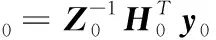
(9)

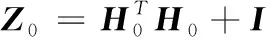
(10)

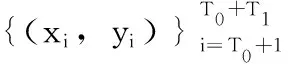
(11)

式中

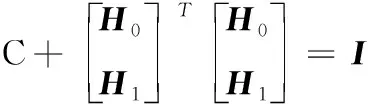
(12)

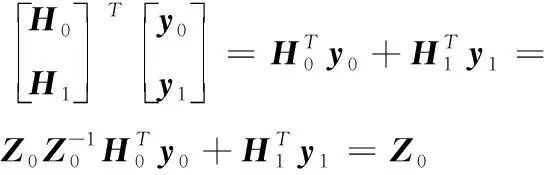
(13)

把式(13)带入式(11)可得

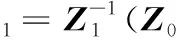
(14)

依次类推，可得递推公式如下

(15)

(16)

(17)

(18)

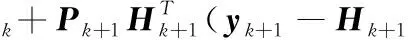
(19)

OS-RELM算法的输出权重在更新时新旧数据占的比重是相同的，对于时变系统，新数据更能体现当前的情况。这里加入遗忘因子，根据新到的数据信息来更新输出权值，对新数据更加敏感，非常适合时变系统[11]。新来的数据个数Tk+1=1，在贯序更新阶段把式(19)变为

(20)

(21)

(22)

(23)

(24)

式中：εk+1为中间变量，λk为第k次的遗忘因子，并且满足0<λk≤1，λk越小，则旧数据的影响越小，第k+1次的遗忘因子公式如下

(25)

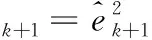
(26)

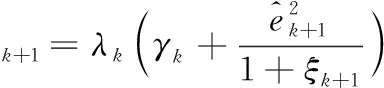
(27)

vk+1=λk(vk+1)

(28)

式中：ρ是一个固定的常数，初始的γ和v是0到1之间的数，遗忘因子越大代表旧数据占的比重越大，遗忘因子越小，新数据占的比重越大。

FFOS-RELM算法具体步骤如下：

1)选取激活函数g(·)，随机产生隐含层参数ai和bi,i=1,2…L。

2)根据式(4)、D0计算H0。

4)令k=0。

(2)贯序更新阶段

1)当第k+1次数据到来时，根据式(4)求得Hk+1。

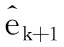
3)如果ξk+1=0，则令Pk+1=Pk；如果ξk+1>0，则根据式(23)、式(24)求得Pk+1。

4)根据式(26)、式(27)、式(28)计算ηk+1、γk+1、vk+1。

5)根据式(25)计算下一步的遗忘因子λk+1，返回(2)中1)继续执行。

2.2 灵敏度剪枝算法

上述的FFOS-RELM算法加入了正则化机制降低了对隐含层节点数的依赖性，但仍然不能确定隐层节点数，这里根据灵敏度剪枝算法来优化初始的网络结构，提高计算的速度和准确度。

2.2.1 灵敏度和网络规模适应度定义

记

kij=gi(xj)=g(aixj+bi)

(29)

i=1,2,…N0

由式(2)可以得到输入为xj时的预测值yj为

yj=k1jβ1+k2jβ2+…+kLjβL

(30)

假设删除第一个节点，则网络的输出变为

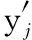
(31)

由式(30)和式(31)可得残差为

(32)

由式(32)可知，根据残差定义第i个节点的灵敏度为

(33)

式中：N0为初始训练样本的个数，kij为第j个输入在第i个隐层节点下的输出，βi为隐层第i个节点的输出权值，可以看出灵敏度越大，代表节点的重要性越大，把灵敏度进行排序，如下所示

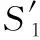
(34)

由灵敏度定义网络规模适应度为

(35)

Mk越大，残差越小，可以设置阈值来确定网络的规模，公式如下

M=minkMk≥θ,1≤k≤L

(36)

式中：θ为设定的阈值，网络规模为M，剔除L-M个节点，阈值的大小通过试凑法得到，为了保存剔除的数据，需要对隐含层参数进一步更新。

2.2.2 权值的更新

剔除的隐层节点参数信息平均加到剩余节点，设M为剩余的节点数，L-M为剔除的节点，记R={i1,i2,…iM}是保留的节点数，D=d1,d2,…dL-M是剔除的节点，则隐层参数更新公式为

(37)

3 Mackey-Glass混沌时间序列的多步预测

混沌系统常用来检验非线性系统性能[12,13]，Mackey-Glass混沌时间序列方程如下所示

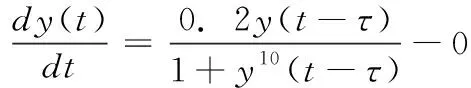
式中：τ为可调的时滞参数，当τ>17的时候出现混沌现象，并且τ值越大现象越明显，利用四阶龙格-库塔法寻找方程的解，用如下方式选取1000个数据

[y(t-18),y(t-12),y(t-6),y(t);y(t+6)]

式中：t=19,20,…,1018，前四项作为输入，最后一项为输出。选取初始的训练数据为150，初始的隐含层节点数为100，初始的遗忘因子λ0=1，γ0、v0为0到1之间的随机数，固定常数ρ=3.8，正则化系数C=1000。灵敏度剪枝算法中的阈值对网络性能影响很大，设置范围为[0,1]，间隔为0.1，仿真结果如图1所示，可以看出随着θ的增大，被删除的节点数越少，RMSE随之变小，从图1中可以看出选取阈值范围在[0.6,1]之间，可以有效表达网络的结构。

图1 网络规模适应度和隐含层节点的关系

综合考虑预测的时间和精度，选取γ=0.7，此时剩余的节点数为37。比较不同算法下以平均绝对值误差、均方根误差和时间，公式如下

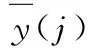
与OS-RELM、FFOS-RELM算法进行比较，结果见表1。

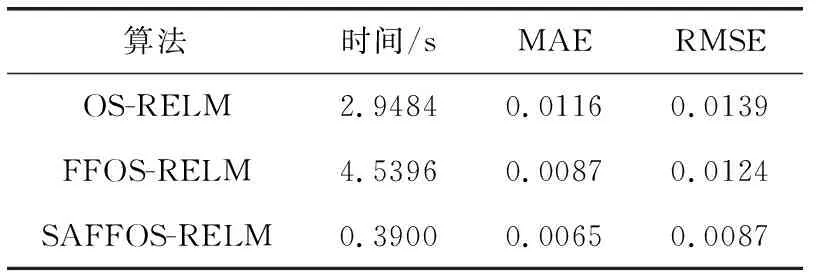
表1 6步预测的结果

从表1可以看出，FFOS-RELM算法由于加入了遗忘因子，预测的准确性得到了很大的提升，并且训练时间和OS-RELM几乎一样，SAFFOS-RELM对初始的网络进行了剪枝，得到了更加紧凑的网络结构，可以看出大大节省了预测时间，并且预测精度也得到了提高，为了更直观观察，图2画出了不同算法下的误差曲线。

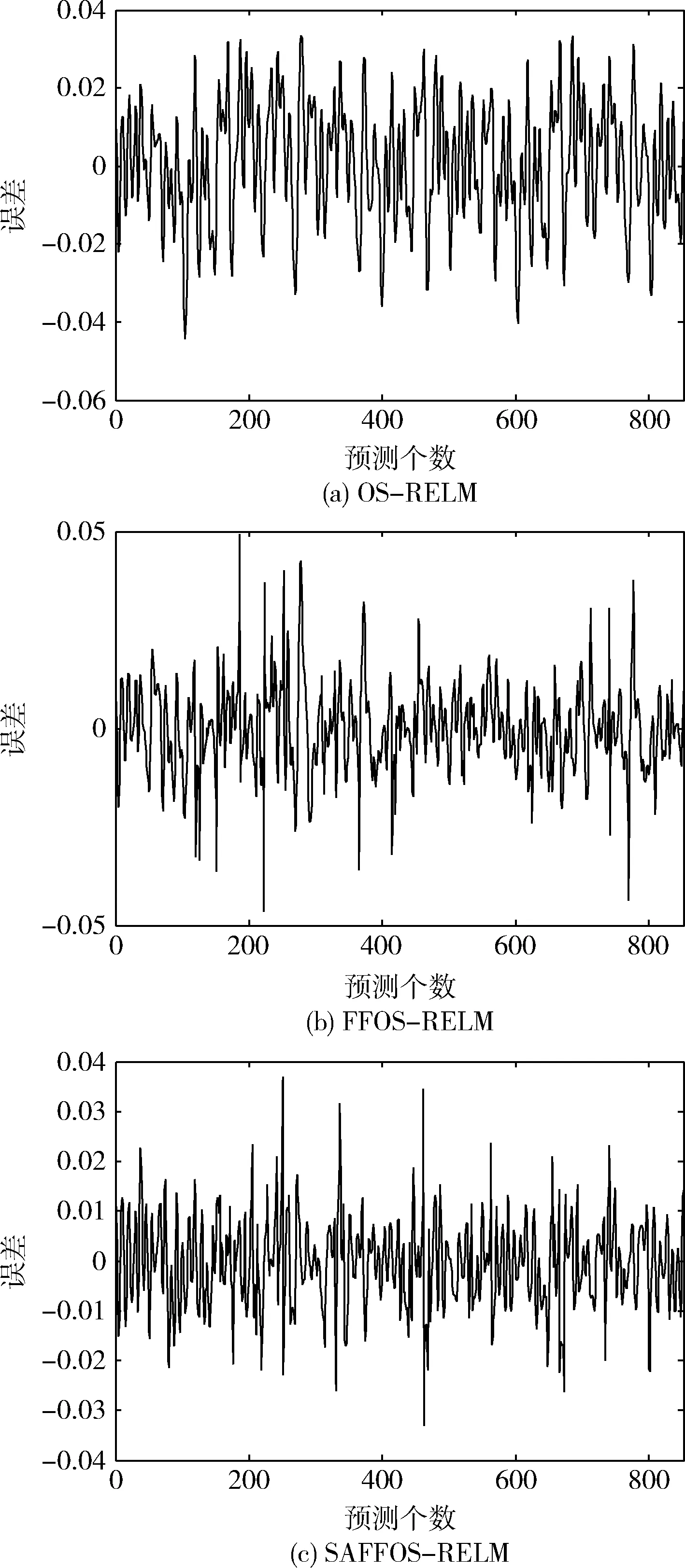
图2 入口氮氧化物误差曲线

4 入口氮氧化物时间序列预测

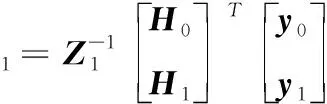
为了进一步验证SAFFOS-RELM算法的有效性，实验数据选取某660M电厂的脱硝系统，数据之间的间隔为10 s，通过对数据进行剔除异常值处理，选取了不同负荷下的320个数据，对数据进行归一化处理，方便网络的计算。初始的训练数据T0=150，隐含层个数为100，正则化系数C=1000，初始的遗忘因子γ0=1，γ0、v0为0到1之间的随机数，固定常数ρ=3.8，网络规模适应度阈值θ=0.8，剩余的节点为25。入口氮氧化物的预测模型如下

y(t+D)=f(y(t-1),y(t-2),…y(t-Δ))

其中，D为预测步长，Δ为嵌入维数，选取Δ=4；对数据进行多步预测，这里选取D=3，并计算预测时间、绝对值平均误差、均方根误差，并和OS-RELM、FFOS-RELM算法进行比较，见表2。

从表2中可以看出，预测的平均绝对值误差和均方根误差从大到小为：OS-RELM、FFOS-RELM、SAFFOS-RELM，因为加入自适应遗忘因子的FFOS-RELM算法可以根据新到的数据改变旧样本和新样本之间的权重，预测精度得到了提高，加入灵敏度剪枝算法得到更加紧凑的网络，提高了网络的泛化能力；预测时间从大到小为：FFOS-RELM、OS-RELM、SAFFOS-RELM，剪枝算法使网络结构更紧凑，运算速度得到了大大的提升，并且因为删除了隐含层冗余节点数，提高了预测精度。图3给出了在不同算法下的预测值和真实值，图4给出了不同算法下的相对误差，由图4可以看出SAFFOS-RELM的相对误差在3%以内，可以有效地预测。

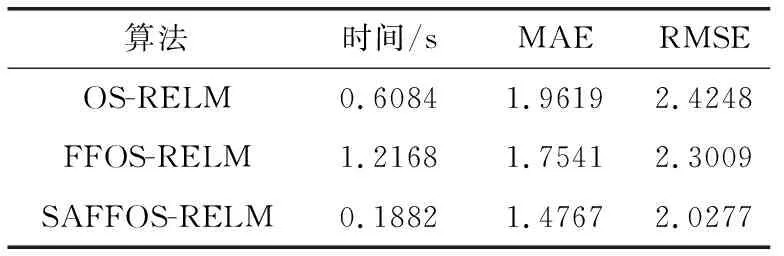
表2 3步预测的结果

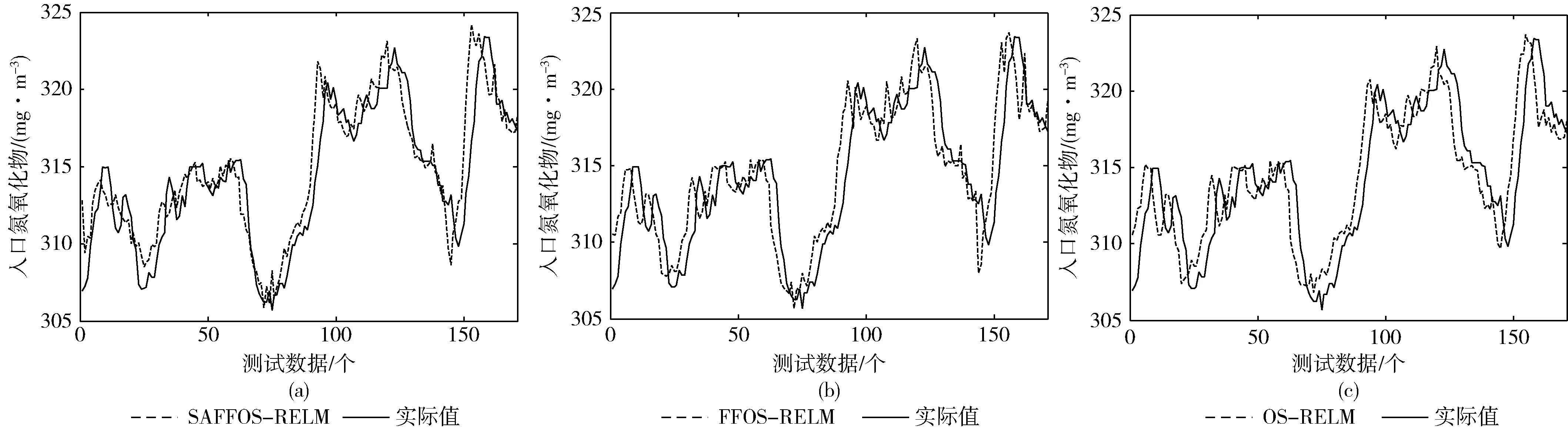
图3 入口氮氧化物的3步预测结果

图4 入口氮氧化物3步预测相对误差

5 结束语

本文提出了一种基于遗忘因子与灵敏度剪枝的极限学习机(SAFFOS-RELM)。加入自适应遗忘因子，赋予了新旧样本不同的权值，更加适用于时变系统，利用灵敏度剪枝算法对初始的网络结构进行优化，删除了网络中的冗余节点，得到最佳的网络结构，以Mackey-Glass混沌时间序列和入口氮氧化物时间序列为例验证了算法的泛化能力。仿真结果表明，SAFFOS-RELM算法的计算时间和模型泛化能力都要优于FFOS-RELM、OS-RELM算法，对于工业中的其它时变系统的时间序列也同样适用。