基于遗传算法的大规模社交网络社区发现算法

陈永建，周 艳,2，刘超英

(1.肇庆学院 计算机科学与软件学院、大数据学院，广东 肇庆 526061； 2.西北工业大学 自动化学院，陕西 西安 710129)

0 引 言

在社交网络中，社区是一个重要的结构，社区内的节点互相具有大量的连接，社区间的节点则仅有少量的连接[1-3]。搜索社交网络中的社区结构能够有助于预测网络的行为、分析网络的功能，目前社区发现问题已经成为社交网络的研究重点。对于大规模社交网络，社区的数量极大并且社区之间的连接也较为复杂，这为大规模社交网络中社区发现算法的准确率与计算效率带来了困难[4]。

许多研究人员已经提出了大量的方案来解决社交网络的社区发现问题，其中一部分算法基于网络的统计分析与聚类分析检测出连接密集的节点集合[5]，但这些算法往往需要一些网络的先验信息，例如：社区数量、网络中社区是否重叠、社区规模等等[6]，而这些先验信息在实际应用中往往难以预知。文献[7]设计了定量描述社区结构的模块性Q函数，随之出现许多元启发式算法将Q函数作为目标函数，从而检测出网络的社区结构，这些元启发式算法包括：模拟退火算法[8]、种群智能算法[9]、遗传算法与演化算法[10]等。遗传算法具有较强的全局寻优能力，因此将遗传算法应用于社区发现问题得到了最为广泛的研究，并且也获得了较好的效果。文献[11]为遗传算法引入了多维染色体与均匀块交叉算子，能够较好地刻画社区重叠部分的节点，但该算法对于社区重叠的社交网络具好较好的性能，而对于社区不重叠的社交网络并未表现出优势。文献[12]为遗传算法引入了免疫机制，该机制能够保证种群的多样性，并且设计了新的染色体编码方案，有效地缩小了种群的搜索空间。文献[13]为了解决遗传算法易于陷入局部最优与缺乏稳定性的问题，设计了基于网络局部信息的节点-社区隶属度机制，该机制能够有效地缩小初始化种群的搜索空间，但该算法的隶属度机制主要考虑了社区内部的隶属度。文献[14]为遗传算法引入了强化学习机制，将agent编码为网络的一个划分方案，并且设计了一系列新的遗传算子，包括：邻居节点竞争算子、混合邻居节点交叉算子、自适应变异算子与自学习算子。上述算法对于遗传算法的改进主要关注于遗传算法的种群多样性、收敛速度以及初始化种群的搜索空间，但如果预测出大规模社交网络的社区数量，能够极大地缩小初始化种群的搜索空间，并且能够提高种群演化的准确性。

当前的社交网络中普遍存在社区重叠的现象，因此许多社区发现算法在计算节点与社区隶属度的过程中，将重叠社区作为先验知识，这类算法[11]无法适用于非重叠社区的社交网络。本文设计了一种基于遗传算法的社区发现算法，采用遗传算法搜索Q函数的最优解，选择随机节点的邻居节点与邻接节点作为初始化种群，并且设计了节点对社区的隶属度计算方案，通过设置合适的阈值能够控制检测的社区规模，该方案也能够预测网络中的社区数量，为社区的规模进行约束，提高种群演化的准确性。因为本算法的社区隶属度计算方案同时考虑了节点的社区内部关联性与外部关联性，因此能够同时适用于社区重叠与社区不重叠的社交网络。

1 背景知识

1.1 社区发现的模块性

模块性是社区发现研究中应用最为广泛的目标函数，能够定量地描述社区的结构，并且形式简洁、易于计算。模块性表示了网络中连接社区结构内部节点的边占网络总边数的比例与一个随机网络中连接社区结构内部节点的边占网络总边数比例的差值，模块性函数(Q)定义为下式

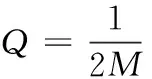
(1)

式中：M表示网络中边的总数量，下标i与j表示网络的两个节点，Ki与Kj分别是第i个节点与第j个节点的度，参数aij表示邻接矩阵第i行、第j列的元素，δ(i,j)表示第i个节点与第j个节点之间的关系，如果节点i与节点j在同一个社区内，那么δ(i,j)=1；否则，δ(i,j)=0。对于社交网络的社区划分问题，Q值越大，表示社区结构性越强，一般社区划分较为明显的Q值范围为0.3～0.7。本文的遗传算法将Q值作为适应度函数。

1.2 基于重叠与非重叠区域的社区隶属度

该文设计了一个基于关联节点的社区数量估计算法，该估计算法考虑了网络连接的整体结构。采用两个参数描述每个节点的社区隶属度，分析社区的重叠部分与非重叠部分。参数IA(内部关联性)表示某个节点与邻居节点的连接情况，该参数度量了社区内节点的内部关联性，IA已经足以检测出社区的非重叠部分，但难以检测出社区的重叠部分。另一个参数EA(外部关联性)度量了网络中每个节点在不同社区之间的作用量，采用生成随机模块模型[15]实现该参数。最终，一个节点属于某个社区的概率依赖该节点的邻居节点数量以及该节点与其它社区的作用量，将这两个度量指标定义为节点的社区关联度。

考虑一个一般性的网络结构，表示为图结构G=(V,E)，其中V与E分别表示网络的节点集与边集合。社区发现问题可建模为搜索节点的分组ci，可将ci表示为C=c1∪c2∪…∪ck。

1.2.1 非重叠区域的内部关联性

内部关联度(IA)评估了每个节点与其所属社区的关联性，具体定义为下式

(2)

式中：N(vi)是节点vi的邻居节点，P(vj|ci)表示节点vj对于社区ci的社区传播概率，该值由边聚类算法[16]推导而来，N(vi)等于节点vi的邻居节点数量。

1.2.2 重叠区域的外部关联性

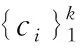
图1是重叠社区与非重叠社区的网络示意图。通过模块模型可检测每个节点与其它社区的外部关联度，每个节点外部关联度的计算步骤如下：

步骤1 估计两个社区之间的作用矩阵；

步骤2 基于邻居节点的社区传播概率与作用矩阵计算给定节点的外部关联度。

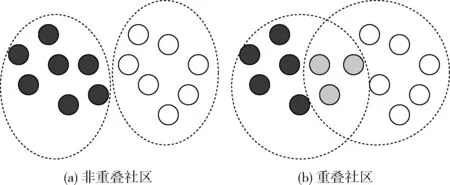
图1 非重叠社区与重叠社区的网络

2 针对社区发现的遗传算法

针对社交网络的社区发现问题提出了一种遗传算法，采用模块性函数(Q函数)引导遗传算法的演化过程，并且设计了不同的策略与遗传算子来识别网络的社区。

随机初始化策略的网络节点之间缺少关联性导致初始解的质量较低，影响了遗传算法的寻优能力与收敛速度。为了解决该问题，设计了一种初始化方案，将原网络图中连接的相邻点作为初始化空间，该方案有助于提高算法的收敛速度；然后，采用社区密度指标度量个体数据的结构，从而平衡各个社区的规模。

本文的社区初始化机制有以下两种：

(1)一级邻居初始化机制：图2是初始化机制的示意图，随机选择一个节点(图中为节点3)，将节点3与其一级邻居纳入初始化社区中，如果达到预设的最大社区规模，则结束搜索过程。如果节点3没有一级邻居，则重复上述过程直至达到预设的最大社区规模。

(2)二级邻居初始化机制：图2是初始化机制的示意图，随机选择社区内一个具有一级邻居的节点(图中为节点3)，将节点3的二级邻居纳入初始化社区中，如果达到预设的最大社区规模，则结束搜索过程。如果节点3没有二级邻居，则重复上述过程直至达到预设的最大社区规模。

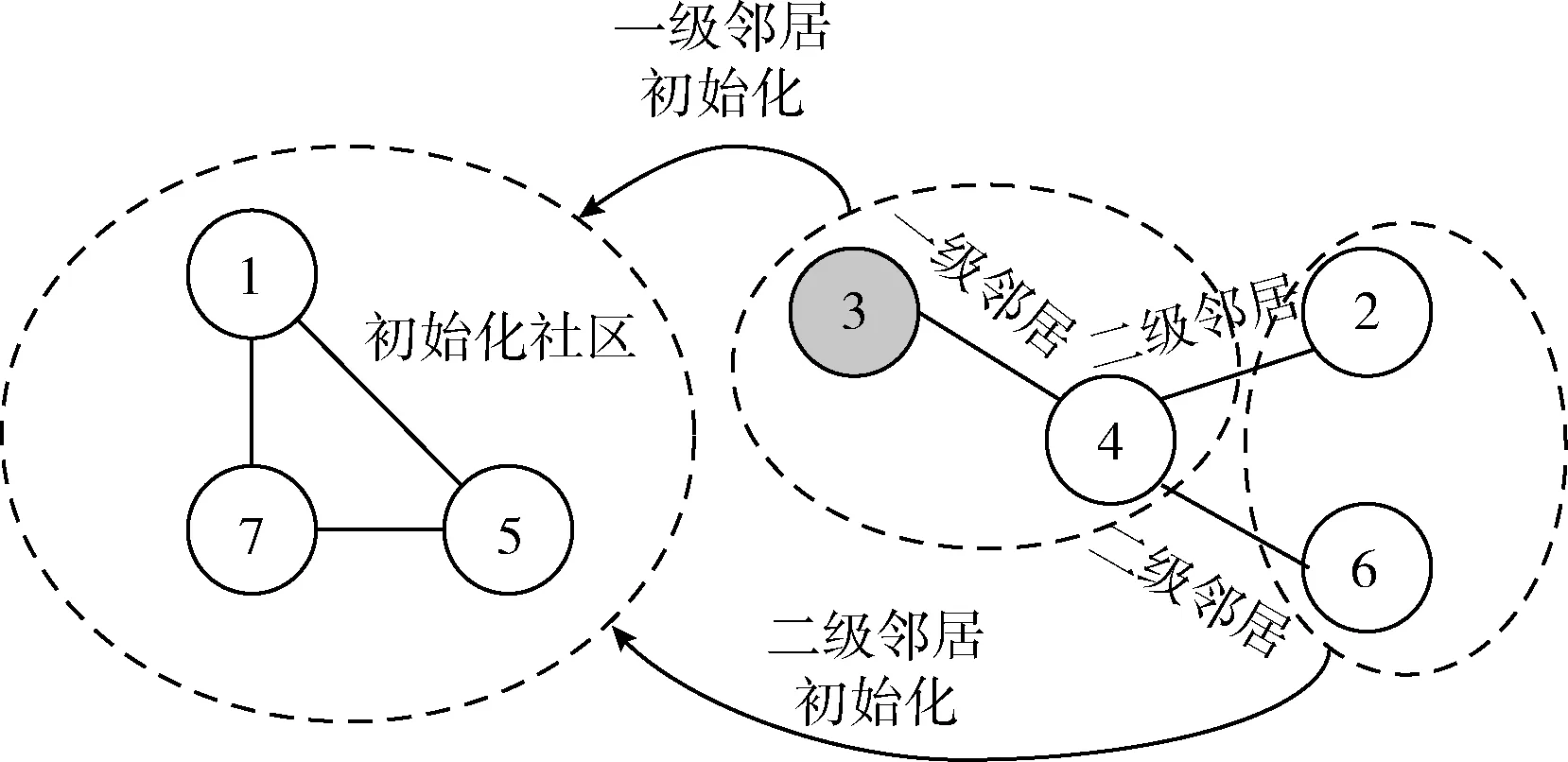
图2 一级邻居初始化与二级邻居初始化

2.1 种群初始化方案

在初始化阶段，使用估计的社区数量(1.2小节)计算每个社区的最大规模，采用平衡初始化机制计算最大规模值：将网络节点总数量除以估计的社区数量，计算结果称为社区密度，将该值作为初始化种群中每个社区的最大规模值。然后开始邻居社区初始化程序，如果①一级邻居初始化机制未能达到最大的社区规模，则开始②二级邻居初始化过程。图3(a)是种群初始化的一个实例。

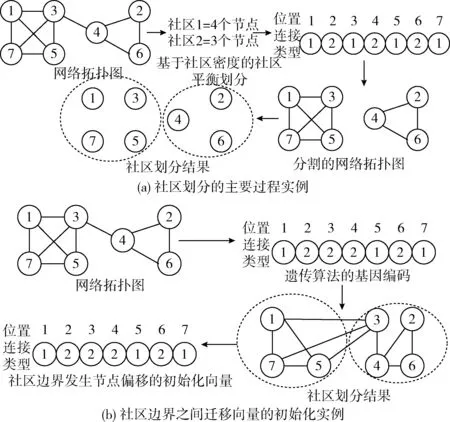
图3 社区初始化实例

种群演化的过程中，两个社区边界之间的节点可能发生迁移，迁移策略是基于边向最有吸引力目标迁移的思想，即给定一个节点，该节点将迁移至该节点连接的最大规模社区。边界之间迁移向量的初始化方案，如图3(b)所示。表1是边界迁移的产生方法，表1的列表示了社区1与社区2，节点数量直接与列节点连接。列迁移向量按照所有社区计数器中的最高值(最多连接数)选择每个节点的最终目标社区。

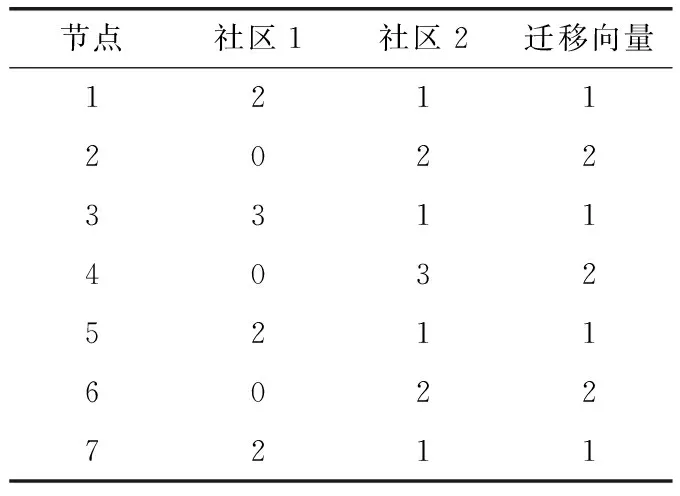
表1 边界迁移的产生方案

2.2 基于社区隶属度的社区发现规模控制

在许多实际应用中，社区结构的数量是已知值，能够缩小搜索算法的搜索空间；而在其它的多数场景下，社区结构的数量是未知值，但可以估计出社区结构的数量，据此也可以缩小搜索空间。预测或者预知社交网络中社区结构的数量，能够有效地缩小搜索空间，并且提高算法的性能。

网络中的社区规模存在巨大的差异，为了满足可控制的社区发现算法，设计了基于社区隶属度的社区发现规模控制方案。通过节点的社区隶属度估计出网络中不同规模的社区数量，如果用户请求搜索大规模的社区结构，则可以设置较大的社区隶属度阈值，从而减小网络中的目标社区数量，该机制能够有效地缩小遗传算法的搜索空间；如果用户请求搜索网络中的全部社区结构，则可以设置较小的社区隶属度阈值。

图4是社区隶属度的计算方法的流程框架，包含了节点的内部关联性与外部关联性。

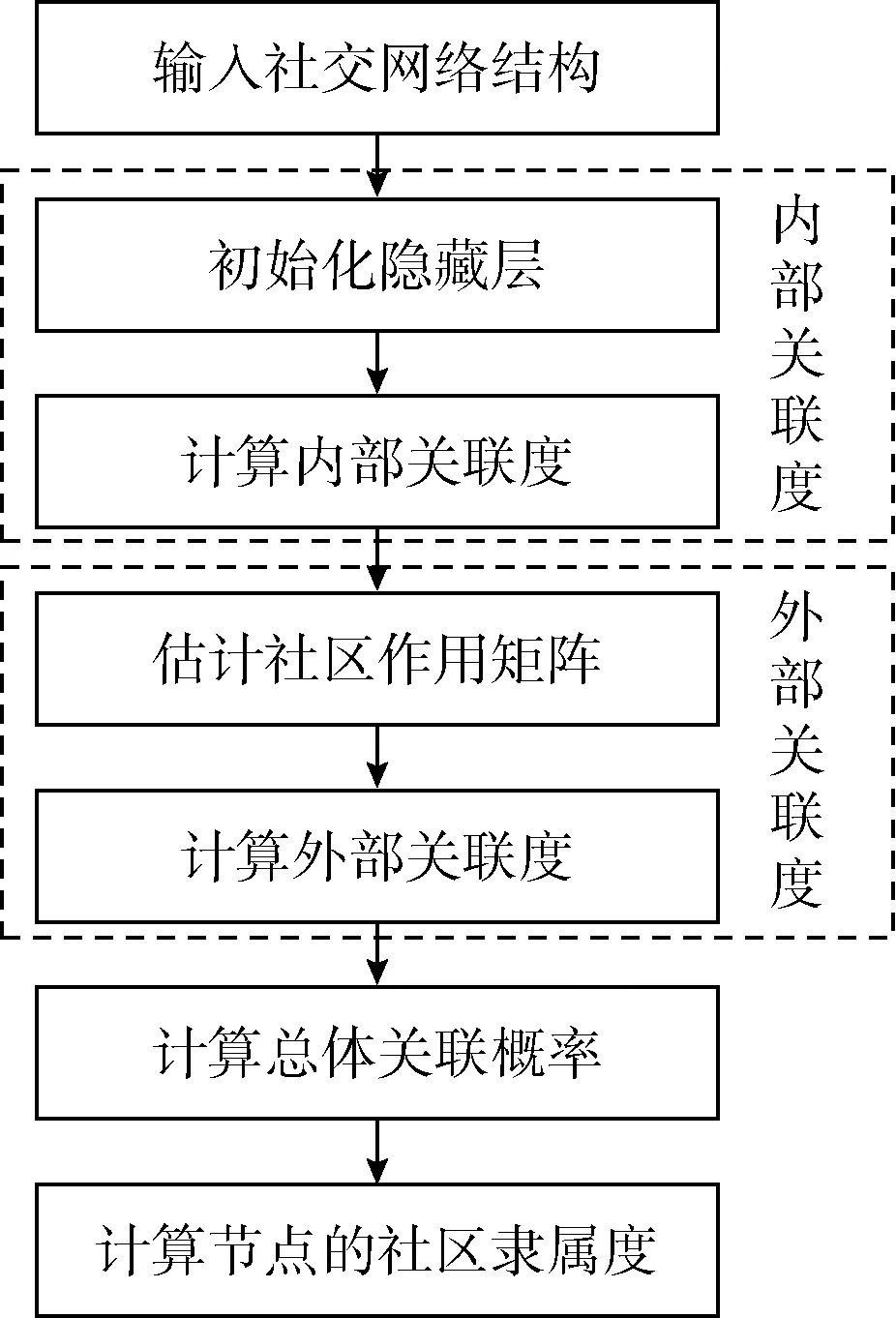
图4 社区隶属度算法的流程框架

假设网络由相互关联的社区组成，网络中每个节点与社区具有两层关联性，第一层是同一个社区节点之间的内部关联性，第二层是节点与其它社区的外部关联性。该文提出一个基于概率的隶属度方法，检测出网络的社区数量。

将每个节点vi对于社区ci的概率隶属条件定义为下式

P(vi∈ci)=P(vi∈ci|N(vi)∈ci)+
P(vi∈ci|N(vi)∈c-i)

(3)

P(vi∈ci)=P1(ci).IAci(vi)+p2(ci).EAci(vi)

(4)

(5)

式中：β(ci,cj)是社区ci与cj之间的作用矩阵。通过最大似然估计方法获得每对社区之间的近似作用矩阵

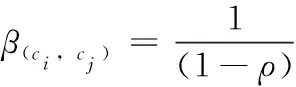
(6)

式中:ρ是已知的稀疏正则化因子，ρ的计算方法为[17]

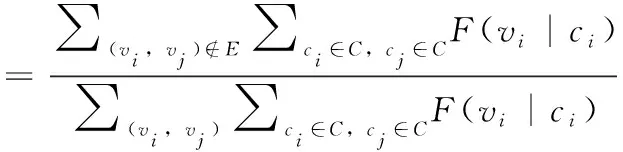
(7)

式中：F(vi|ci)=max(P(vi|ci)×P(vj|cj),P(vi|cj)×P(vj|cj))。

图5是3个社区重叠的实例，节点v4同时属于3个社区，根据式(2)～式(6)可计算出图中：ρ=39/53，βc1,c2=1.25，βc1,c3=0.8，βc2,c3=1，EAv4(c1)=53/70，EAv4(c2)=45/70，EAv4(c3)=46/70，IAv4(c1)=2/7，IAv4(c2)=3/7，IAv4(c3)=2/7。计算出节点的内部关联性与外部关联性之后，最终传播概率依赖权重值p1与p2，p1与p2的计算方法如下

(8)

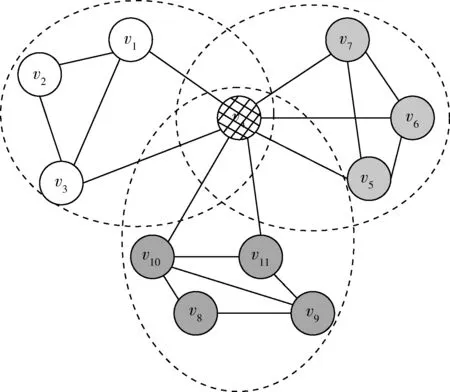
图5 3个社区重叠的实例

节点v4同时属于3个社区，根据式(2)～式(6)可计算出：ρ=39/53，βc1,c2=1.25，βc1,c3=0.8，βc2,c3=1，EAv4(c1)=53/70，EAv4(c2)=45/70，EAv4(c3)=46/70，IAv4(c1)=2/7，IAv4(c2)=3/7，IAv4(c3)=2/7。

2.3 遗传算子

为了增强遗传算法对社交网络相关数据结构的寻优效果，设计了特殊的遗传算子。

2.3.1 交叉算子

交叉算子基于社区边界间节点的交换而实现，将目标社区边界的一个节点与当前社区的另一个节点进行交换，并且目标社区不应是当前的社区。第二个节点应当满足其社区最优的外部关联性(第1.2小节描述)。通过选择外部关联性最优的节点进行交叉操作，有助于维护社区之间规模的平衡。图6是交叉算子的操作实例，在该实例中，选择节点3作为互换节点，其目标社区是节点1，图6中目标社区的节点是与源社区(社区2)关联性最高的社区，选择这两个社区的节点进行交换。列“节点”列出了外部连接的数量，选为交换的节点是具有最多邻居数量的节点：节点3有3个外部连接，节点5有1个外部连接，选择节点5与节点3交换。

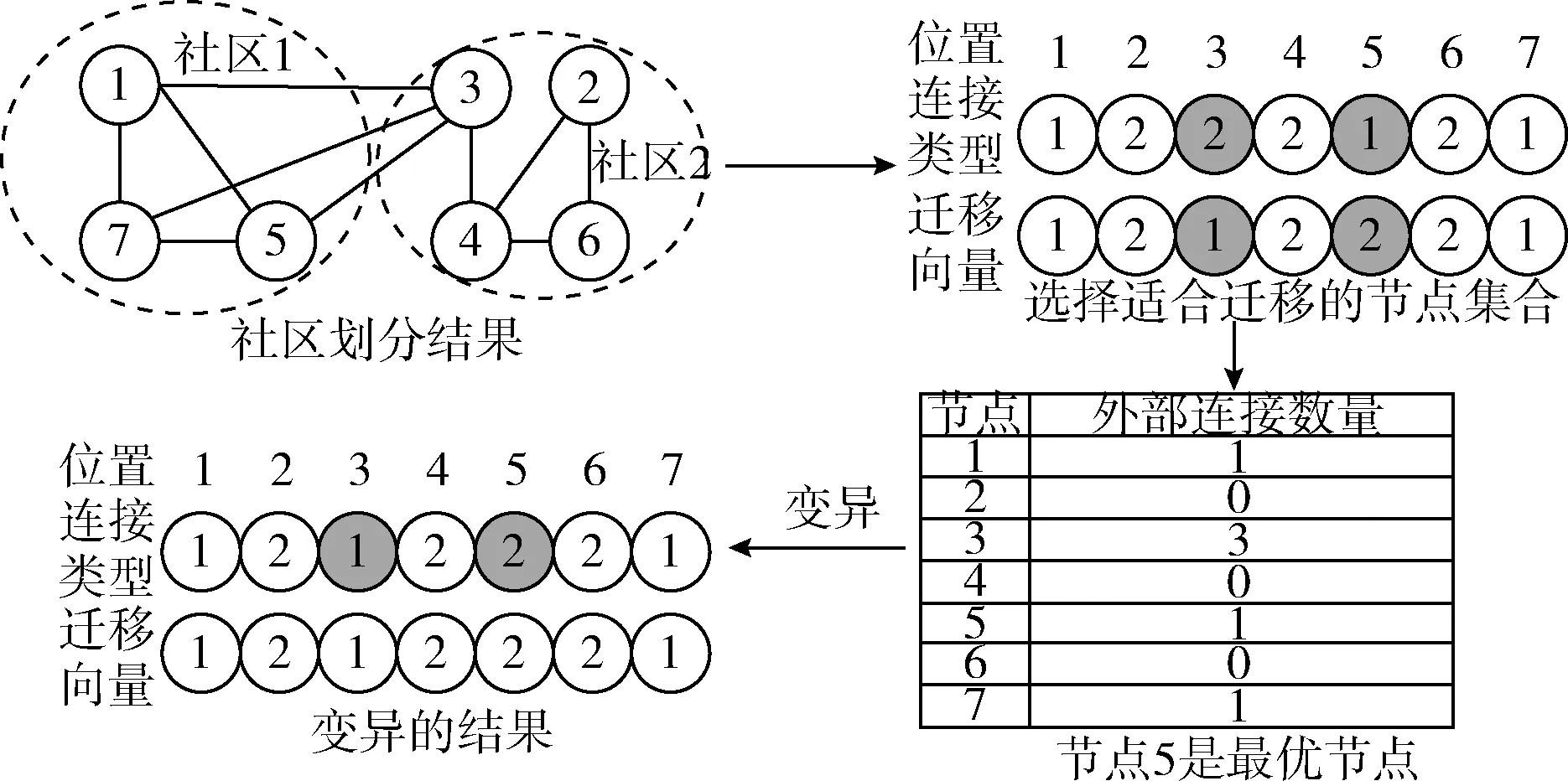
图6 交叉算子的操作实例

2.3.2 变异算子

选择适合变异的节点集，从该节点集中随机选择一个节点，将该节点与目标社区的一个节点进行交换。图7是变异算子的操作实例，在该实例中，目标社区的节点是与源社区(社区2)关联性最高的社区，选择这两个社区的节点进行变异操作，关联性最高的社区能够提高寻优效果。计算的复制(reproduction)节点数量为2，然后随机选择两个复制节点，将节点5复制为节点2。

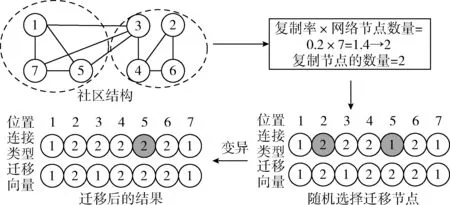
图7 变异算子的操作实例

3 仿真实验与结果分析

将本算法与其它基于遗传算法的社区发现算法以及非基于遗传算法的社区发现算法进行了对比分析，综合评估本算法的性能。实验环境为PC机，CPU为Intel Core i7，2.4 GHz主频，8 GB内存。基于Matlab编程实现本算法。

3.1 性能评价指标

NMI(标准化互信息)是社区发现问题中常用的性能评估指标，NMI定义为下式

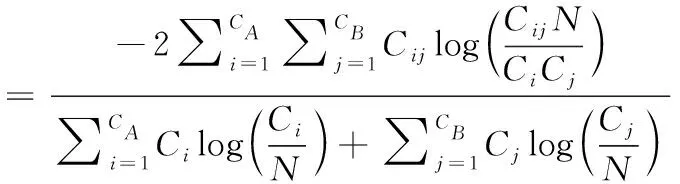
(9)

式中：网络的两个部分A与B构成了混淆矩阵C，Cij表示属于A部分中社区i与B部分中社区j的节点数量，CA与CB分别表示A与B部分的社区数量，Ci表示A部分中社区i的节点数量，N表示节点的总数量。如果A=B，那么NMI(A,B)=1；如果A与B完全不同，那么NMI(A,B)=0。NMI值越接近1，说明算法划分的社区结构与最优网络结构越相似。

3.2 参数配置

目前已经具有许多基于遗传算法的社区发现算法，为了评估本文本算法的有效性，首先将本算法与其它基于遗传算法的社区发现算法进行比较，分别为IGA[12]、GAOM[13]、MAGA[14]。

为了确保对比的公平性，所有的遗传算法采用相同的参数设置，具体见表2。

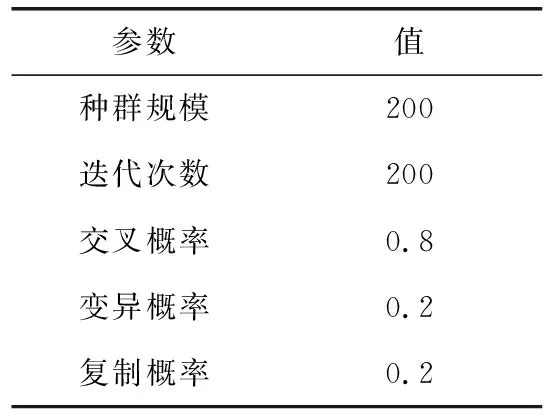
表2 遗传算法的仿真实验参数

3.3 与基于遗传算法的社区发现算法比较

3.3.1 benchmark数据集

采用4个常用的公开社交网络数据集作为benchmark数据集，评估4个基于遗传算法的社区发现算法的性能，4个社交网络的描述见表3。

表3 基于遗传算法的社区发现算法benchmark数据集

3.3.2 社区发现的准确率结果与分析

每个算法对每个benchmark数据集均独立地运行50次，统计每组数据的平均值与标准偏差。4个算法对4个数据集的社区划分准确性如图8所示。从图中可看出，本算法的NMI平均值与标准偏差均优于其它3个基于遗传算法的社区发现算法，随着社交网络规模的扩大，本算法的优势更加明显。本算法的标准偏差也明显地优于其它3个算法，可看出本算法的社区划分结果具有较好的鲁棒性。

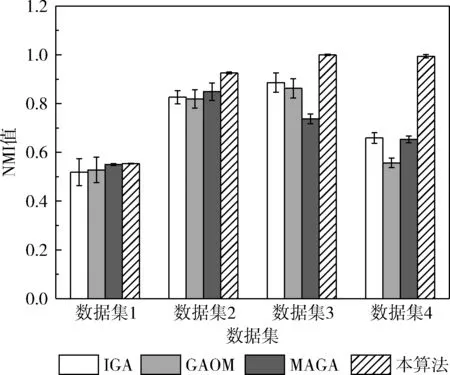
图8 4个算法对4个数据集的社区划分准确性(NMI值)

数据集1的网络规模较小，社区数量也仅有3个，4个社区发现算法的NMI值均较低，遗传算法对于这种小规模数据集的迭代次数较少，并且容易受到初始化种群的影响，因此小规模数据集的性能低于大规模数据集的性能。但是数据集4的网络规模约为数据集1的4倍，而IGA[12]、GAOM[13]、MAGA[14]这3个算法的NMI值却低于数据集2与数据集3，这显示了这3个遗传算法未能较好地考虑社交网络的特点，而本算法设计了基于社区隶属度的社区数量估计算法，对于不同规模的数据集均能够获得较高的准确率。

4个算法对4个数据集的社区划分模块性结果(Q函数)如图9所示。因为4个遗传算法均将Q函数作为适应度函数，因此Q函数的结果直接反映了4个遗传算法的最优解结果，可看出4个算法对数据集1,2,3的模块性结果均在[0.3,0.7]之间，而数据集4提出的最优社区并未考虑模块性，所以导致GAOM、MAGA两个算法的模块性结果小于0.3。

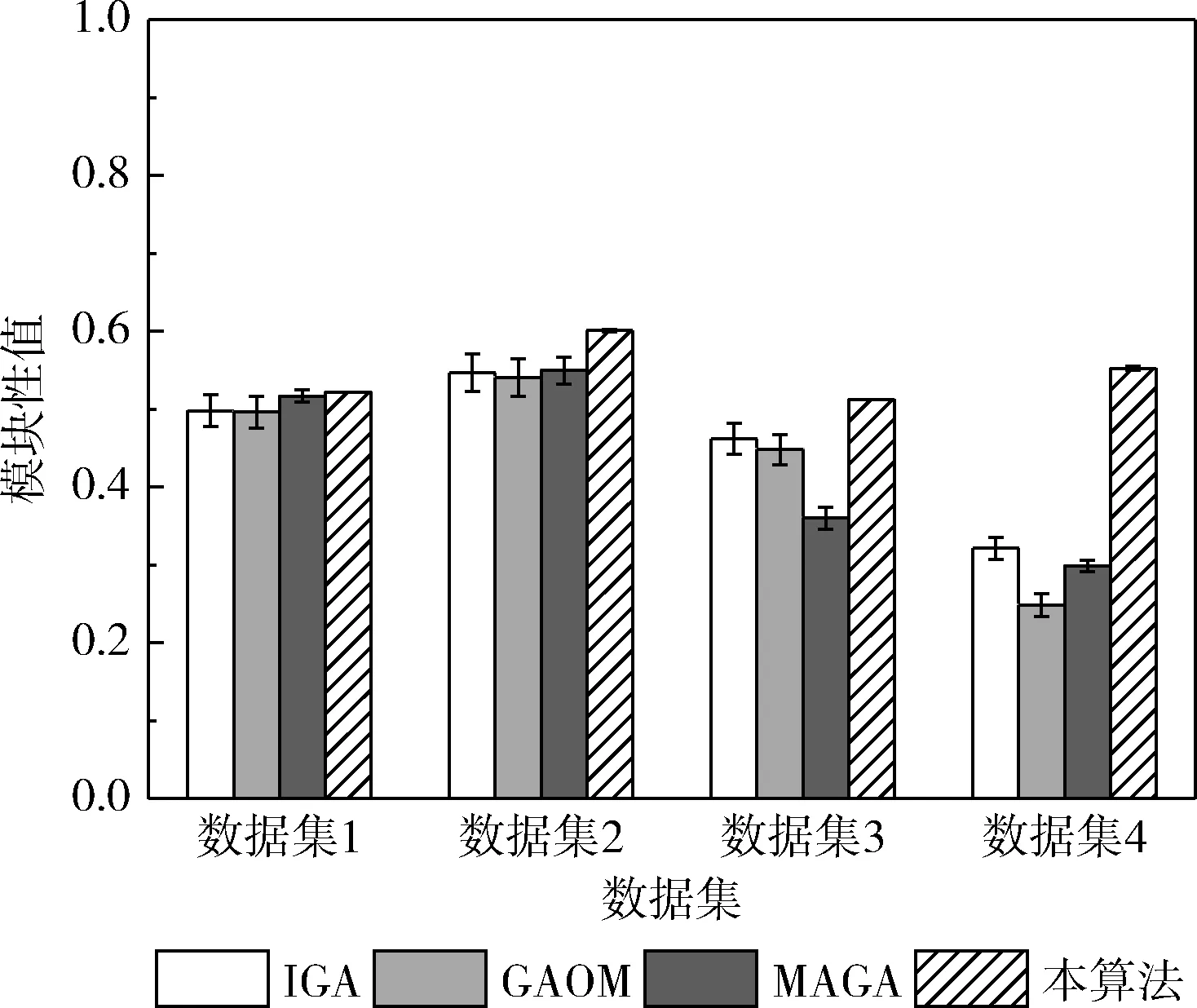
图9 4个算法对4个数据集的社区划分模块性结果(Q函数)

3.3.3 社区发现的时间效率

时间效率是遗传算法的一个重要指标，在此统计了4个遗传算法对于数据集4的计算时间，结果见表4。GAOM算法为了解决遗传算法易于陷入局部最优的问题，其变异算子在每轮迭代过程中均需要计算网络中每个节点的局部信息以及社区隶属度值，遗传算法求解大规模问题的迭代次数往往较多，而GAOM每次迭代的计算量均较大，严重影响了计算效率。MAGA是一种基于agent的遗传算法，该算法的各个agent均需要完成多个复杂的算子，包括：基于分割与合并的邻居节点竞争算子、混合邻居节点交叉算子、自适应变异以及自学习算子，这些算子计算量较大，因此MAGA的收敛速度也较慢。IGA通过免疫机制约束了遗传算法的初始化种群，缩小了初始化搜索空间，因此收敛速度较快，计算速度也较快。本算法将社交网络中的邻居节点与邻接节点纳入初始化种群中，并且设计了基于社区隶属度的社区数量估计算法，有效地减小了网络的社区空间，并且能够快速地引导种群的演化过程，本算法获得了最低的计算时间，此外，计算时间的标准偏差为0.0077，因此本算法的计算效率具有较好的稳定性。

表4 4个社区发现算法对于数据集的计算时间(单位：秒，每组实验独立运行50次，统计平均值与标准偏差)

3.4 与一般社区发现算法比较

3.4.1 benchmark数据集

因为本算法的社区隶属度估计算法考虑了重叠社区与非重叠社区，因此本文采用两种类型的真实数据集评估本算法的性能，分别见表5与表6，表中给出了重叠社交网络与非重叠社交网络的结构介绍。10个数据集的网络规模均较大，能够测试本算法对于大规模社交网络的性能。

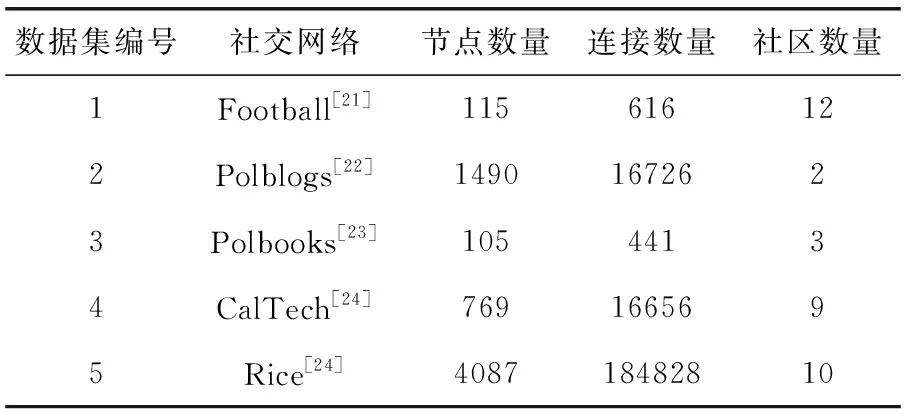
表5 重叠社区结构的社交网络

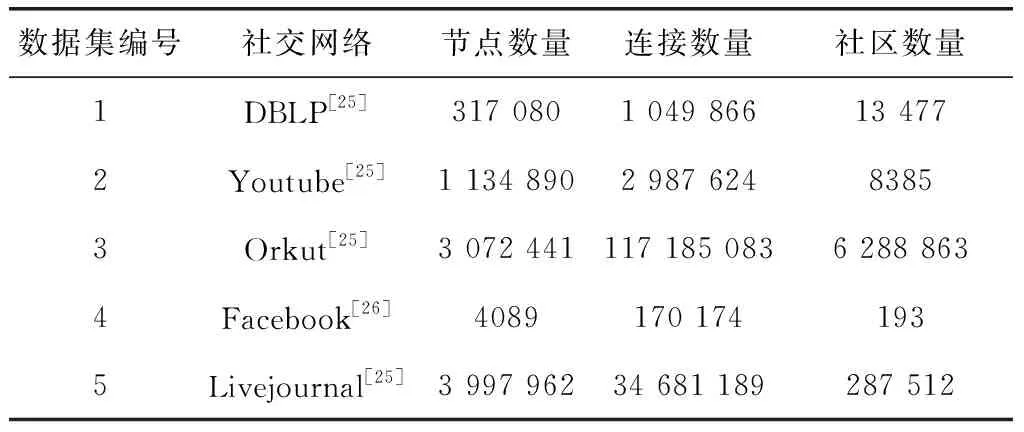
表6 非重叠社区结构的社交网络

3.4.2 实验结果与分析

COMBO、NISE是两个近期性能较好的社区发现算法，并且这两个算法同时支持重叠社区与非重叠社区的社交网络，因此将本算法与这两个算法进行比较。首先对5个重叠社区的社交网络进行实验，每组实验独立运行50次，统计NMI的平均值与标准偏差，结果如图10所示。可看出，本算法对于数据集1,2,3,4的社区检测准确率均优于其它两个算法，数据集5的最优社区划分方案并未考虑模块性，而本算法成功搜索出最优的模块性结果，但是与数据集5提出的最优社区划分方案仍然有一定的差异，因此本算法对于数据集5的NMI值较低，略低于其它两个算法。

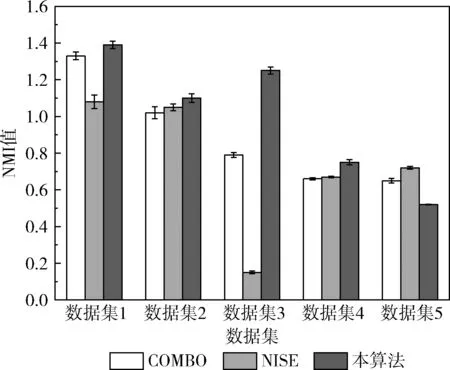
图10 3个算法的对于社区重叠社交网络的社区检测NMI结果

然后对5个非重叠社区的社交网络进行实验，每组实验独立运行50次，统计NMI的平均值与标准偏差，结果如图11所示。可看出，本算法对于数据集1,2,3,4的社区检测准确率均明显地优于其它两个算法，数据集5中包含大量位于社区边界的节点，并且这些节点与其它社区的距离均较为接近，3个社区发现算法对于数据集均获得了较低的NMI值，3个算法的结果较为接近。

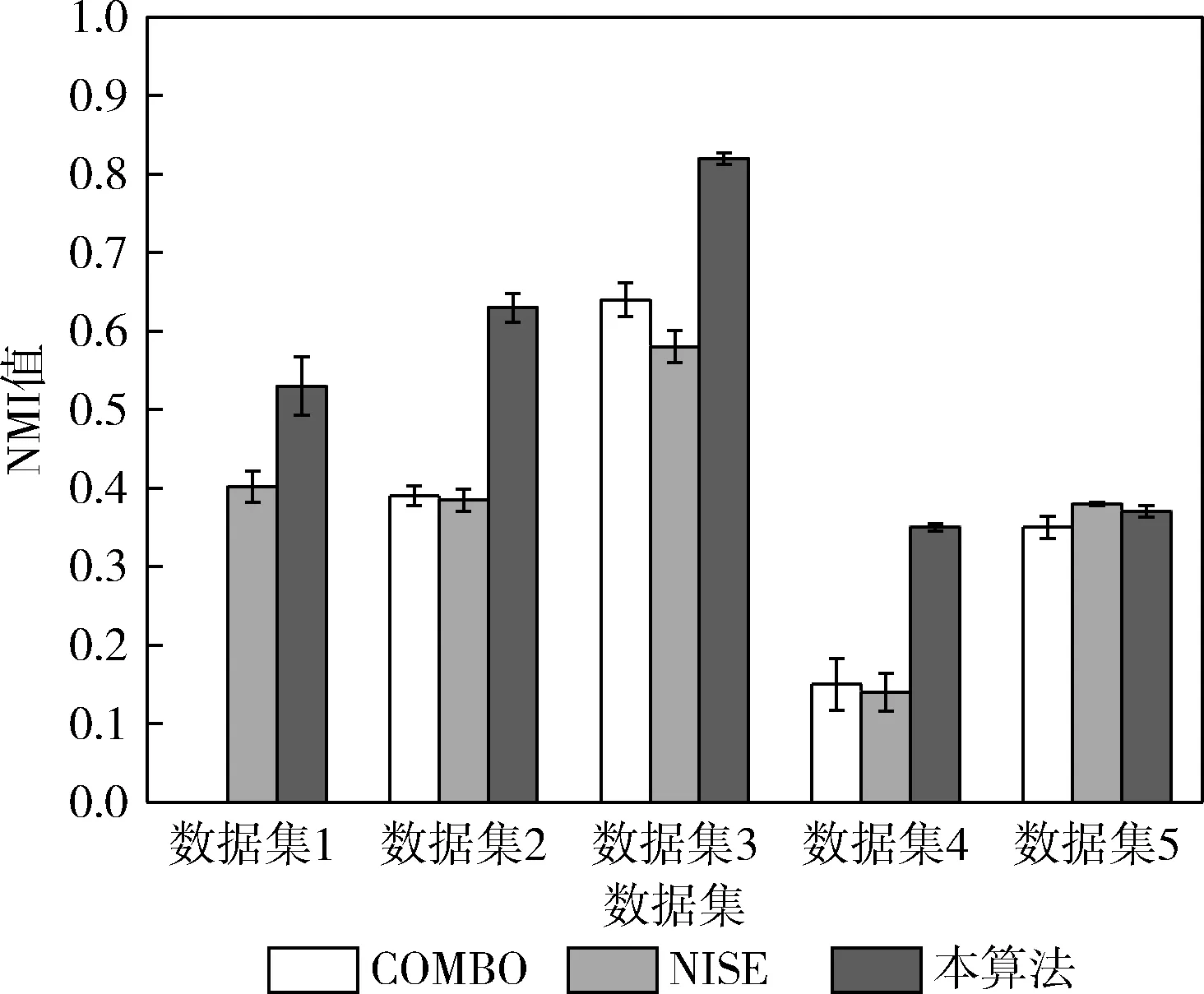
图11 3个算法的对于社区不重叠社交网络的社区检测NMI结果

4 结束语

为了提高大规模社交网络社区发现算法的准确率与计算效率，设计了一种基于遗传算法的社区发现算法，采用遗传算法搜索Q函数的最优解，选择随机节点的邻居节点与邻接节点作为初始化种群，并且设计了节点对社区的隶属度计算方案，通过设置合适的阈值能够控制检测的社区规模，该方案也能够预测网络中的社区数量，为社区的规模进行约束，提高种群演化的准确性。因为本算法的社区隶属度计算方案同时考虑了节点的社区内部关联性与外部关联性，因此能够同时适用于社区重叠与社区不重叠的社交网络。该算法对于大规模数据集也具有较高的社区检测准确率。

因为本算法是一种基于社交网络模块性的社区发现算法，如果社区的重叠部分存在密集的连接，则会影响社区的模块性，这为本算法的社区检测准确率带来不利的影响，未来将重点关注不满足社区模块性的社交网络问题。