基于整数混沌和DNA编码的并行图像加密算法

胡辉辉，刘建东，商 凯，陈 飞

(1.北京化工大学 信息科学与技术学院，北京 100029； 2.北京石油化工学院 信息工程学院，北京 102617)

0 引 言

近年来的研究表明，DNA计算具有许多良好的特性，例如，大量的并行性、巨大的存储量和超低的功耗，十分利于其在图像加密中的应用。Zhang Qiang等[1]提出了一种基于DNA编码与2D Logistic映射的数字图像加密算法，该算法将DNA编码与混沌加密相结合，在一定程度上提高了加密算法的安全性，但也存在着DNA编码的规则有限、低维混沌系统结构简单，使得加密后的图像存在像素相关性强等缺陷，安全性依然不高。

时空混沌系统是一种复杂的动力学系统，十分适合用于设计针对图像等大数据量的多媒体信息的加密算法。目前已有许多基于时空混沌理论的图像加密算法[2-4]，这些加密算多是采用像素位置置乱和像素值扩散的思想，很好地体现了密码设计的混淆和扩散这两个基本原则。由于现有的混沌模型难以产生同时具备独立性和均与性的伪随机序列，降低了加密方案的安全性，而且位置置乱较为耗时，不利于大批量图像数据的加密和实时传输。

结合DNA编码和高维混沌系统的优点，成为设计更加安全、耗时更低的图像加密算法更好的选择[5,6]，然而这些图像加密算法所使用的混沌系统都是三维及以下混沌系统，混沌系统的结构比较简单且复杂度相对较低，降低了加密算法的安全性。本文基于DNA编码和四维以上的高维时空混沌系统，设计了一种并行彩色图像加密算法。算法充分利用了DNA编码、DNA加法和DNA求补等DNA密码的思想，复杂化了图像加密中的基本运算。同时，构造了高维的整数非线性耦合混沌系统，从模型基础上保证了算法所用整数伪随机序列的安全性。实验结果表明，相对于其它加密算法而言，本文设计的加密算法不仅密钥空间无限大，而且易于并行实现，加密速度快，利于图像数据的加密和实时传输的实现，同时还能很好地抵御各种常用的攻击手段。

1 整数非线性耦合混沌系统

时空混沌模型中经典的耦合帐篷映像格子模型(CML)的数学形式为

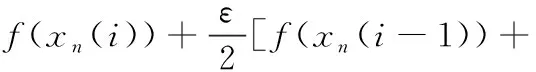
f(xn(i+1))]

(1)

此模型包含了时间上的并行迭代特征和空间上的耦合扩散机理，通过多次并行迭代，很容易产生多维的伪随机序列，但模型产生的多维伪随机序列存在着相邻序列的互相关性过大的缺点，同时，此模型是在实数域内实现的，有限精度的存在既不利于计算机高速计算的实现，又使得数字化混沌系统的动力学特性相较于连续系统而言存在着严重的退化。

为解决相邻序列的互相关性过大的问题，引入Arnold猫映射的方法，采用猫映射作为模型的空间格点耦合方式，解决了原模型相邻序列的互信息值过大的问题。其次引入动态整数Tent映射构造整数非线性耦合混沌模型，模型在整数域内实现，从而消除了有限精度对系统的不良影响。

由此构造了整数非线性耦合混沌模型，其数学形式为

xn+1(i)=[f(xn(i))+f(xn(j))+f(xn(k))]mod(2a)

(2)

式中：2a表示系统可容纳的最大状态值，n为迭代步数；i=1,2,…,L为格点坐标，L为系统格点数，且L大于等于4；边界条件由xn(L+1)=xn(1)，xn(0)=xn(L)实现，初始条件xi∈[1,2a-1]。

非线性函数f选择动态整数Tent映射,其数学形式为

(3)

gi=xi+kimod2a

(4)

式中：系统的位数为a，xi∈[1,2a-1]，ki是Tent映射的水平移动距离。

空间格点位置i，j，k之间由猫映射决定

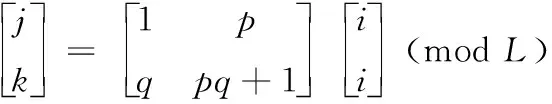
(5)

其中，p和q是映射参数。

以下分别从独立性(互信息)和均匀性(分布特性)两个最根本的密码学特性对整数非线性耦合混沌模型产生的整数伪随机序列进行密码学特性分析。

1.1 互信息分析

互信息显示了不同序列之间的统计约束程度，当两序列完全相关时互信息值最大，反之，两序列相互独立时互信息值为零。

图1和图2分别给出了两种模型取100个空间格点、格点两两之间的互信息值。对比图1和图2可知，整数非线性耦合混沌模型很好地解决了耦合帐篷映像格子模型(CML)所产生的多维伪随机序列中相邻序列间互信息值过大的问题，不同序列之间的互信息值都接近于零，任意格点的伪随机序列都接近于相互独立。

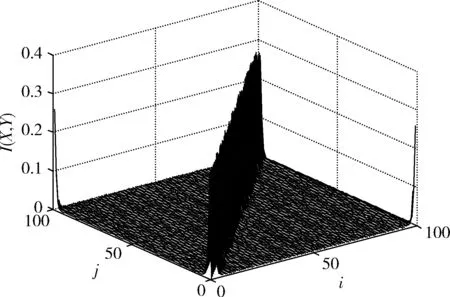
图1 CML模型的互信息

1.2 序列不变分布特性分析

混沌伪随机序列的不变分布特性能够直观地展示出各点状态在不同取值区间的分布概率。

图3和图4分别给出了CML模型和整数非线性耦合混沌模型所产生的混沌伪随机序列的不变分布特性曲线，对比两图可知整数非线性耦合混沌模型产生的伪随机序列具有良好的均匀分布特性，远优于CML模型。

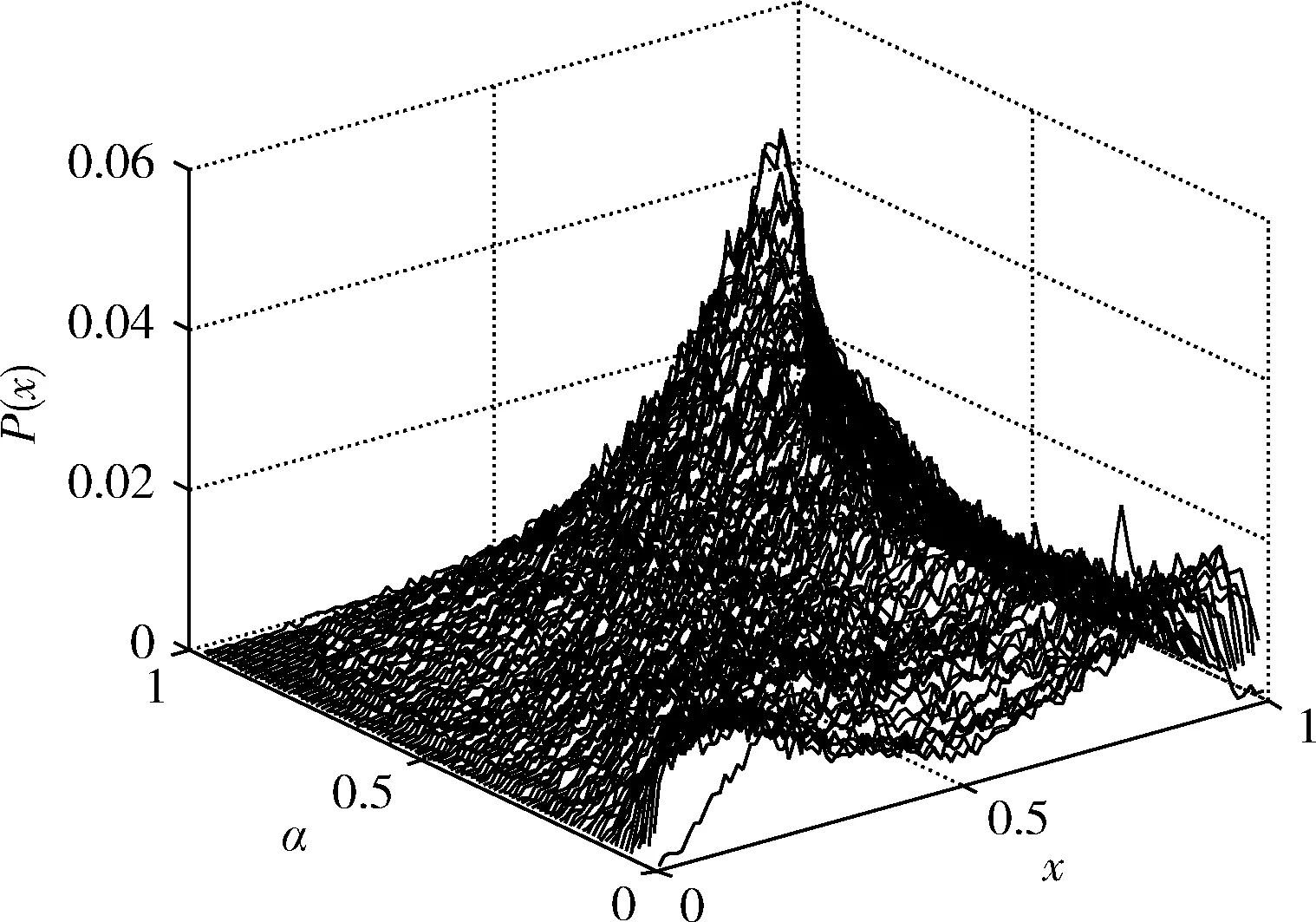
图3 CML模型随α变化的不变分布概率曲线

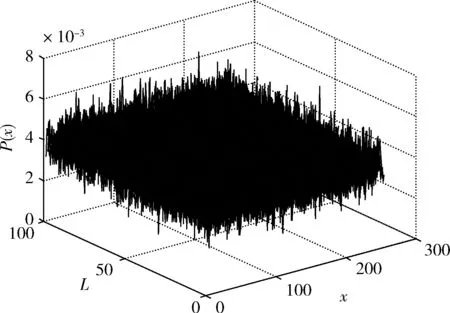
图4 整数非线性耦合混沌模型的不变分布概率曲线

通过对整数非线性耦合混沌模型所产生的混沌伪随机序列从独立性和均匀性两个最根本的密码学特性进行仿真分析，结果表明了本文构造的整数非线性耦合混沌模型能够快速、并行地产生多维混沌伪随机序列，序列的密码学特性优良，能够从根本上解决目前混沌伪随机序列发生器难以产生同时具备均匀性和独立性的多维序列的缺陷。

2 DNA序列

2.1 DNA序列操作

每个DNA序列都是由A、G、C、T这4种核酸碱基组成，其中A与T，C与G互补配对。在现代的计算机理论中，所有的信息都是由二进制数字0和1表示，且0和1是互补的，因此00和11、01和10也是互补的。在4！=24种编码规则中只有8种满足互补规则，见表1。

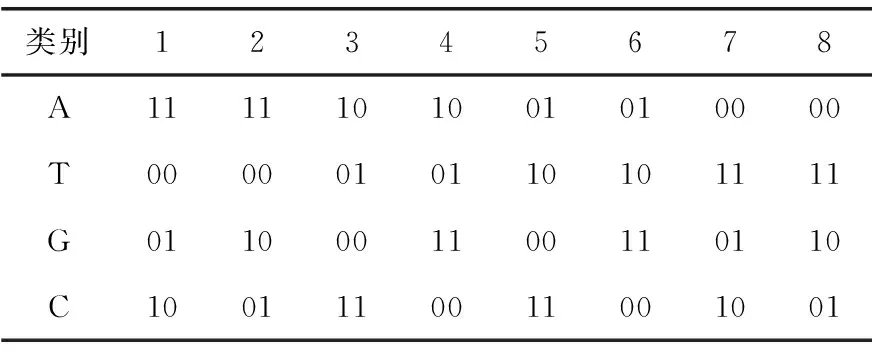
表1 满足互补规则的8种DNA编码规则

2.2 DNA互补规则

互补规则必须满足条件：对于核酸串中的每个核酸xi有

(6)

式中：B(xi)是xi的基对(base pair)，它能保证单映射的互补规则成立。

2.3 Hamming距离

在DNA计算中，Hamming距离用于计算两个长度相同序列相应位置具有不同项的数目。序列x=(x1,x2,…,xn)和y=(y1,y2,…,yn)的Hamming距离H(x,y)可定义为

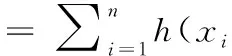
(7)

2.4 DNA序列的加减法代数运算

DNA序列的加法和减法是在两位二进制下按照传统加法和减法运算进行的。与8种DNA编码规则对应，存在8种DNA加法规则和8种DNA减法规则。在进行运算时应注意，所有加减运算都只有2位。

3 彩色图像加密方案

整数非线性耦合混沌模型能快速、并行地产生性能良好的多维整数混沌伪随机序列，这使得此模型能够十分便利地应用于图像加密算法中。基于此模型和DNA编码，本文设计了一种并行的彩色图像加密算法。算法主要包含3个部分：图像数据与整数伪随机序列按位异或混淆灰度值、中间密文按DNA编码规则进行求补运算、RGB三分量两两做DNA加法运算。其中第一部分的按位异或能够很好地发挥整数伪随机序列良好的均匀性和随机性优势；第二部分的求补运算以整数伪随机序列为参考量来决定是否进行求补运算，从而增大了算法的复杂度；第三部分三分量相互做DNA加法运算彼此混淆，既很好地保证了算法对于明文的敏感性，又再次混淆了图像的灰度值。图5给出了算法的流程图，具体加密步骤如下：

(1)读取彩色图像，得到图像数据矩阵E[3,N*N]，并计算3个汉明距离H1,H2,H3(加密解密时都使用原图的汉明距离)；

(2)给定L,p,q,k,H1,H2,H3及其它初值，生成混沌序列，并与图像数据做按位异或运算，得到中间密文P1[3,N*N](使用序列a1,a2,a3)；

(3)对P1进行DNA编码(编码规则b1),得到P2[3,N*N*4]；

(4)当混沌序列数值大于127时，对图像编码序列求补得到P2[3,N*N*4](使用序列a4,a5,a6)，求补规则为(A:00，T:11，G:01，C:10；A-T-C-G-A)；

(5)深入开展水权试点研究工作。开展相关专题研究，探索层次分析法与模糊决策理论，建立适宜黑龙江省实际情况的水权分配指标体系，构建初始水权分配模型，开展水权初始配置应用研究，编制五常市、庆安县、肇州县等试点水权确权实施方案，探索开发考虑第三方影响的市场供需平衡的水权转让均衡定价技术方法，为黑龙江省水权试点工作推广提供技术支撑。

(5)图像R/G/B三原色矩阵P2[3,N*N*4]相互混淆做DNA加法得矩阵E[3,N*N*4]。相互混淆规则为(R=r+g、G=g+b、B=g+2b)；

(6)对E进行DNA解码(解码规则b2),得到密文图像矩阵[3,N*N]。

图5 加密算法流程

解密步骤是加密步骤的逆过程。首先将密文图像进行DNA编码，再对密文图像三分量进行DNA减法运算进行混淆，相互混淆的规则为加密时混淆规则的逆运算，即(r=R+B-2G、g=2G-B、b=B-G)；然后选择同样的伪随机序列进行逆求补，规则为(A∶00，T∶11，G∶01，C∶10；A-G-C-T-A)；之后对密文图像进行解码，再与伪随机序列执行按位异或运算即可得到解密图像。

4 并行实现与实验结果

4.1 算法的并行实现

本文设计的彩色图像加密算法的主要理论基础是整数非线性耦合混沌模型和DNA编码及运算，前者能快速、并行地产生性能良好的多维混沌伪随机整数序列，后者本身也具备着高并发性易于实现的特性。因此，本文基于C#编程环境，充分利用.NET4.0及以上版本所提供的一个新的命名空间System.Threading.Tasks及其附属的Parallel静态类(System.Threading.Tasks.Parallel)，简单方便地发挥了多核计算机中多个逻辑内核的作用，高速并行地对算法进行了编程实现。并行程序主要包含彩色图像三分量加密过程中的Task类命令式任务并行和大循环计算时的Pa-rallel类命令式数据并行两大部分。

算法的实验环境为64位Windows系统，处理器为Intel(R)Core(TM) i7-2600CPU，3.4 GHz。针对算法，分别进行了并行编程实现和串行编程实现，以标准测试图像Lena彩色图像为例，运行算法所花费的时间统计为表2。同时表2也给出了文献[7]对相同大小的彩色图像加密的算法耗时和文献[8]对相同大小的灰度图像加密的算法耗时。对比表中数据可知，对于不同尺寸大小的彩色图像，本文设计的算法的并行实现都能稳定达到串行实现的两倍速度以上。同时，算法并行实现的速度为文献[7]设计的算法的两倍左右，文献[8]设计的算法的3倍左右。

表2 算法耗时统计

4.2 算法实验结果

采用Visual Studio 2013平台，取512×512像素大小的Lena彩色标准图像作为明文图像进行实验。实验结果如图6所示，图6可以看出，通过加密算法对实验图像进行加密，能够完全隐藏原图所包含的直观信息，达到很好的保密效果，并且通过解密算法能够无损地恢复原图。

图6 算法加密效果

5 算法安全性分析

5.1 密钥空间及敏感性分析

(1)密钥空间

对于任何的加密算法来说，密钥空间的大小都直接决定了其安全性的高低，当密钥空间较小时，就不可避免地会受到穷举攻击等暴力破解攻击。本文算法采用了可变长度的整数非线性耦合混沌模型，其空间格点大小可以任意选取(L≥4)，与之对应的空间格点初始值的数量也是可变的，因此其密钥空间可变，且可以无限大。本文可以选作密钥的变量只要有两个部分：一是混沌系统的初始值以及系统参数，二是加密过程中选取的混沌序列所在空间格点位置以及DNA编码、解码和求补规则的选取。当今的密码算法普遍认为密钥空间大于2^100就相对安全，本文算法中当取10个空间格点时，其密钥空间为：256^13×8^6×6^3×10^6=2^131×3^3×5^6≈2^146，满足密钥空间安全性要求。若将空间格点数增加到25，其密钥空间将超过2^256，同样将空间格点数增加到55，其密钥空间将超过2^512，密钥空间的安全性完全可以通过增加空间格点数量得到足够的保证。

(2)密钥敏感性分析

在实验中，对512×512像素大小的Lena彩色标准图像加密后，分别采用正确密钥和错误密钥解密，敏感性分析如图7所示，改变其它密钥参数也能得到相同结果。可知在解密过程中，即使密钥只发生了微小的变化，解密过程也变成了一轮新的加密过程，无法得到正确的解密图。

图7 密钥敏感性

5.2 抗统计攻击分析

(1)直方图分析

图8给出了Lena彩色图像加密前的明文图像和用本文算法加密后的密文图像的各分量灰度直方图。对比可知，密文图像各分量的灰度直方图都呈现均匀分布的特点，很好地隐藏了原图的统计信息。

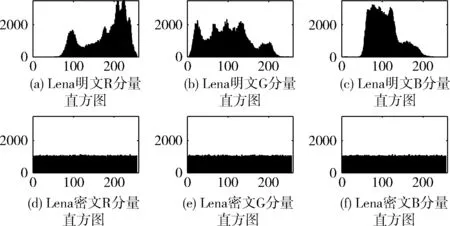
图8 灰度直方图分析

(2)相邻像素相关性分析

相关系数是用来分析和度量相邻像素之间的相关程度的指标，密文相关性越低，相关系数越接近于零。对明文图像和密文图像分别随机选取了5000组相邻像素，从水平、垂直和对角线3个不同方向计算密文图像的相邻像素相关系数，见表3，同时，表3也给出了文献[8]中密文图像的相邻像素的相关系数。对比表中数据可知，使用本文算法加密得到的密文图像相邻像素相关系数更接近于零，这表明明文图像所包含的统计特性已经充分扩散到密文图像中，算法可以抵抗统计分析攻击。

表3 密文图像相邻像素的相关性系数

(3)信息熵测试

信息熵可以用来表征图像像素分布随机性的强弱。由于图像像素值的取值有256种可能，所以图像数据信息熵的最大理想值为8。表4给出了512×512的Lena彩色图像的明文和几种加密方案对其进行加密后的密文图像的信息熵，对比表中数据可知本文算法能够得到的密文图像的信息熵更为接近理想值8。

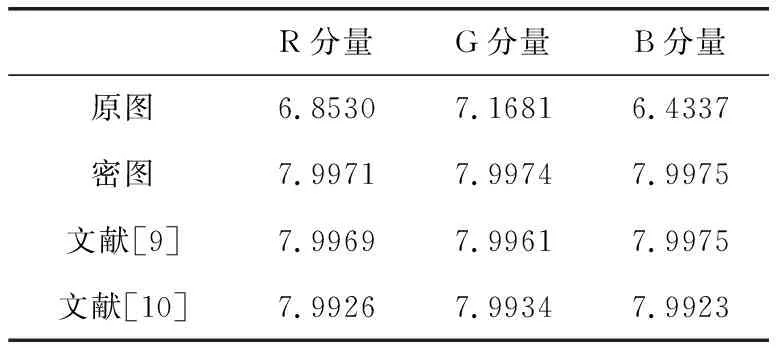
表4 Lena图像信息熵比较

5.3 抗差分攻击分析

差分攻击是常用的已知明文攻击的攻击方法，图像加密算法要做到能够抵抗差分攻击，就必须对明文足够敏感。一般使用像素变化率(NPCR)和归一化像素值平均改变强度(UACI)这两个指标来衡量加密算法对明文的敏感性，其理想值分别为99.6094%和33.4635%[11]。

表5给出了本文算法和另外两种不同加密方式的NPCR和UACI值。对比表中数据可知，本文设计的加密算法更能抵抗差分攻击。

表5 明文敏感性分析比较

6 结束语

本文首先构造了一种基于整数非线性耦合的时空混沌模型，通过仿真分析验证了此模型能够快速、并行地产生多维整数混沌伪随机序列，且序列同时具备均匀性和独立性，从而克服了混沌伪随机序列发生器设计中存在的根本性缺陷。

基于此模型，设计了一种使用DNA编码的彩色图像加密算法，并利用多核处理器的优点对算法进行了并行实现。算法主要包含3个部分：图像数据与整数伪随机序列按位异或混淆灰度值、中间密文按DNA编码规则进行求补运算、RGB三分量两两做DNA加法运算。实验结果表明本文提出的彩色图像加密算法密钥空间可变且足够大，算法能够有效地抵抗统计分析攻击和差分攻击，安全可靠，算法的并行实现使得算法的加密速度较串行实现提高了至少两倍，在图像信息的存储和实时传输中具有极大的实用价值。