基于Godunov格式的流域地表径流二维数值模拟

张大伟，权 锦，马建明，向立云

（中国水利水电科学研究院，北京 100038）

1 研究背景

采用水动力学方法模拟地表径流过程有诸多优点，能够更好反映小流域地形、地貌的特点，能够提供整个流域面上的风险点水力要素信息，能够适用于无水文资料的地区，具有更好的扩展性，方便与泥沙模型、水质模型耦合等。由于扩散波和运动波形式简单，数值稳定性相对较好，因此在地表径流模拟中得到较广泛的应用［1-2］，但是对于复杂地形，特别是对于山洪这种洪水形态，采用简化的运动波或扩散波方法会带来较大的计算误差［3-4］。近几年，随着计算机硬件技术和数值计算技术的快速发展，采用完整的二维浅水方程组对地表径流过程进行模拟成为了可能［5-6］。完整的二维浅水方程组除能够提供更准确的水力要素信息外，还能够模拟局部复杂的水流现象，如滚波和水流流态过度现象等。

在浅水数值模拟领域以求解Riemann近似解为基础的Godunov格式已发展得比较成熟，该格式既能模拟光滑解，又能自动适应复杂流态变化，因此得到广泛应用［7-8］。目前，在应用完整二维浅水方程组模拟地表径流方面，该格式依然是主流数值格式［5-6］，但是，直接将已有的基于Godunov格式的浅水模型用来模拟流域地表径流过程时极有可能会出现不合理的计算结果［9-10］。采用完整二维浅水方程组对地表径流过程进行模拟，面对的主要难题是如何在复杂地形上（如坡度大、存在倒坡、地形起伏大）准确模拟水深相对较浅的（小于mm量级）薄层二维水流运动，这一问题与常规洪水（如河道洪水、溃堤洪水等）有明显不同。当前的Godunov模型在地形概化时主要有斜底模型和平底模型之分，斜底模型的地形高程布置在网格节点，平底模型的高程布置在网格单元型心。常规二维洪水演进的干湿变化过程见图1，由图1可见，不论是平底模型还是斜底模型，在常规洪水模拟中，干湿变化一般位于洪水面边缘的位置，但是在降雨径流计算中，干湿变化毫无规律，可能在任意时刻出现在任意网格单元上，再加上坡面径流较浅，坡面离散后，按照现有的干湿处理技术很容易出现水面到处间断的假象。所以，如果再直接采用常规洪水模拟时用到的干湿处理技术，将很难正确反映实际地表水流运动的状态特征。

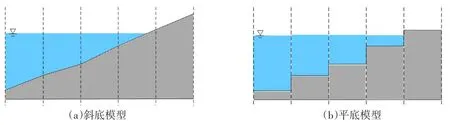
图1 常规洪水的干湿变化过程

综上，将Godunov格式用于流域地表径流模拟时遇到了新的技术问题，即坡面小水深条件下的干湿处理难题。目前这一问题已成为该领域新的热点和难点，很多学者提出了各自的处理方法，如Yu等［11］开发完成的CHRE2D模型，当水深小于10-3m时，采用扩散波计算单元流速；Xia等［12］提出了一种新的水面重建方法来处理底坡源项。已有这些方法均取得了较好的效果，但如何使干湿处理更简洁、模型精度更高依然有很大的研究空间。本文基于非结构网格的Godunov格式，开发一套新的降雨径流二维水动力模型，并与多个经典算例进行验证，最后用于谢家湾流域地表径流过程模拟中。

2 模型开发

2.1控制方程采用的完整守恒型二维浅水方程组如下式所示：

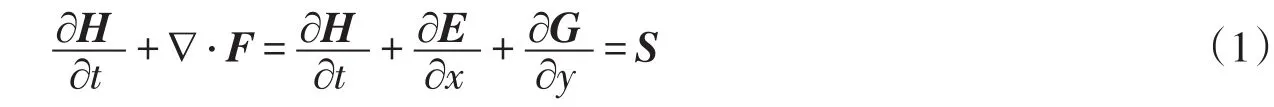
2.2 数值离散方法在坡面流研究领域，作为一个可接受的概念，可以将坡面流设定成为均匀覆盖流域地表的片状薄层水流［13-14］，如图2所示，本文模型开发就是基于这一概念进行的，即采用三角形非结构网格对流域进行离散后，在每个三角形单元内的径流量是沿着地表坡度均匀分布的，以此区别与常规洪水的不同。

整体的数值离散方法依然在有限体积法框架下进行，首先在三角形单元上对式（1）进行积分并进行Green变换后得到下式：

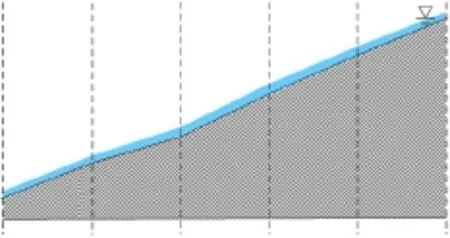
图2 坡面流流动示意图

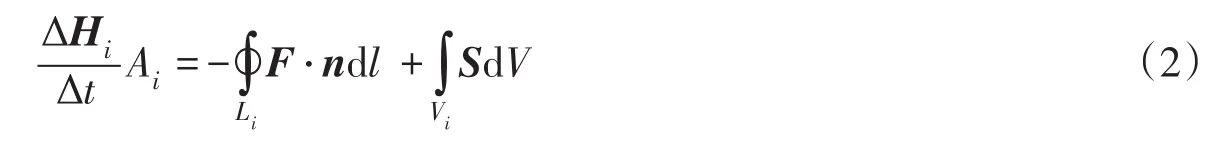
式中：Ai为第i个三角形计算单元的面积；Li为第i个控制单元V的边界；F·n为通过每条边的法向数值通量。

在本模型中，高程点布置在三角形网格节点，以x方向为例，对坡度直接积分：

其中：

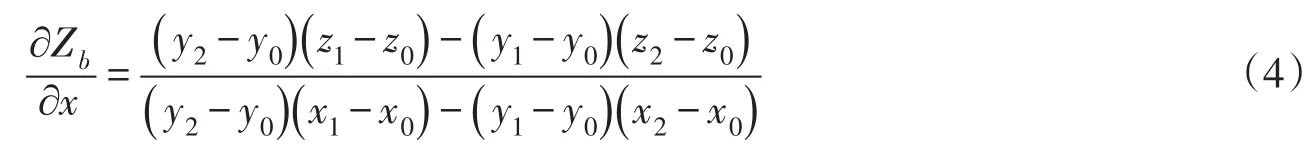
式中：x0、x1、x2、y0、y1、y2、z0、z1、z2分别为三角形单元3个顶点的横坐标值、纵坐标值和高程值，3个点以逆时针顺序排列。

界面通量计算，采用具有广泛应用基础的Roe格式进行求解。为了保持计算格式的和谐性，平衡底坡项直接离散带来的数值误差，需要在经典Roe格式的基础上，加上一修正项［15］，通量计算如下式所示：

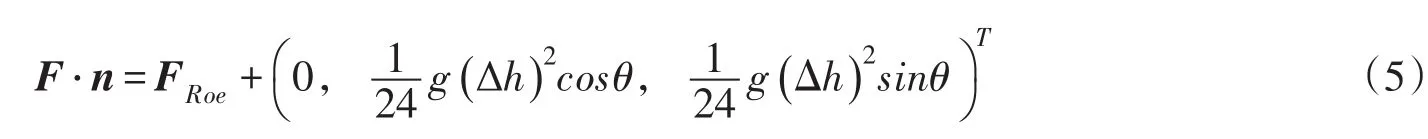
式中：FRoe为经典Roe格式计算公式，详细过程可参见文献［16］；Δh为单元边两端的水深差值；θ为单元边外法线方向与x轴正方向的夹角。

摩阻项具有高度的非线性性质，如果处理不当，很容易带来数值不稳定问题。为了适应降雨径流这种小水深条件下摩阻项的计算，对摩阻项积分采用半隐式方法进行求解［17］，以x方向为例，对摩阻项的计算如下式所示：

将式（6）带入式（2）即可求得时段末的守恒变量(hu)t+1。

在干湿处理方面，由于本文模型采用了片状薄层水流的建模概念（如图2所示），因此干湿处理方法变得异常简洁。提前设定单元干湿判断的水深阈值Htol，当单元计算水深值大于Htol时，则该单元为湿单元；当单元计算水深值小于或等于Htol时，则该单元为干单元。当界面两侧同时为干单元时，认为界面处无质量和动量的交互，不进行界面处数值通量计算；其它情况下，即界面两侧同时为湿单元或一侧为湿单元，另一侧为干单元的情况下正常进行界面处数值通量计算。在进行下一时刻单元的水力要素值更新时，如果一个单元为干单元，与其相邻的3个单元也同时为干单元时，仅在连续方程中考虑该单元在该时段降雨源项的汇入；其它情况下，单元的连续方程和动量方程正常求解。本文采取的这种干湿处理方法，能够很好地反映降雨径流运动的特点，单元水面和地形均不需做任何特殊处理，易于计算机编程实现。对于降雨径流这种小水深条件下的浅水流动，在保持模型稳定的前提下，干湿阈值Htol选取越小越好。在本文采用的验证算例中，Htol取值均为10-10m，在谢家湾流域算例中，Htol取值为10-8m，可完全满足降雨径流条件下数值计算的精度需求。

在本文模型中，仅有Manning糙率系数需要率定，该系数是一个综合系数，雨滴对地表径流的打击效应、地表的摩擦力、微地形影响以及坡面流的表面张力效应等均反映在该系数中。坡面流的阻力规律与一般明渠流的阻力规律是有所不同的，但是目前仍缺乏细致的定量认识，实践应用中，在坡面流的糙率选取时一般还需要借鉴明渠流的糙率选取经验。

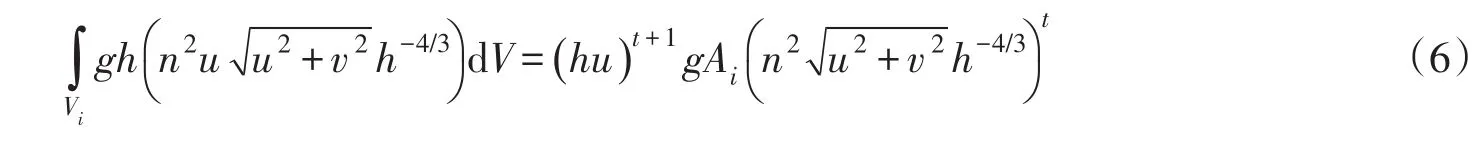
3 模型验证

3.1 一维坡面恒定雨强径流算例该降雨径流试验由Morgali等［18］完成，试验区域是一块长21.945 m（72ft）的覆盖草皮的坡面，坡度为0.04。采用的恒定降雨强度为93 mm/h，坡面糙率系数n=0.5 m-1/3s；降雨过程是一直持续的，计算时间取为1200 s，计算时间大于坡面的汇流时间，因此，出口径流过程的末端是一恒定值。

采用0.1 m的三角形网格来离散计算区域，采用本文研发模型对算例进行模拟，计算的坡面末端径流过程如图3所示。从图3可以看出，模型计算数值解与运动波解析解和实验观测值吻合较好，在起始阶段，计算值比实验观测值略大，分析原因可能是由于在实验初始阶段，降雨被带有草皮的实验坡面吸收、滞留造成的。

3.2 一维坡面非恒定雨强径流算例Govindaraju等［19］设计了该数值算例，算例中，一维坡面长21.945 m（72ft），在工况1中，谢才系数C=1.336 m1/2/s，坡度为0.001；在工况2中，谢才系数C=1.767 m1/2/s，坡度为0.04。两种工况的降雨过程如表1所示。降雨过程在空间上分布是均匀的，但是随着时间变化。计算采用的网格尺寸为0.1 m，总模拟时长80 min。模拟结果如图4所示，由图4可以看出，本模型计算结果与文献［19］提供的该算例的近似解析解吻合的非常好，说明模型对非恒定降雨过程的模拟是成功的。

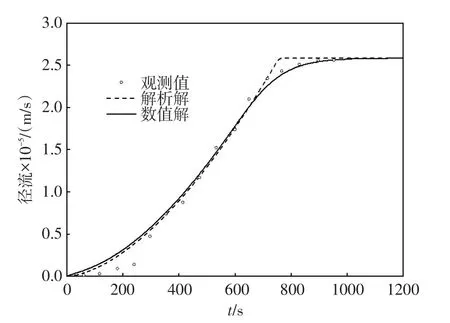
图3 恒定雨强算例计算结果

表1 降雨过程数据

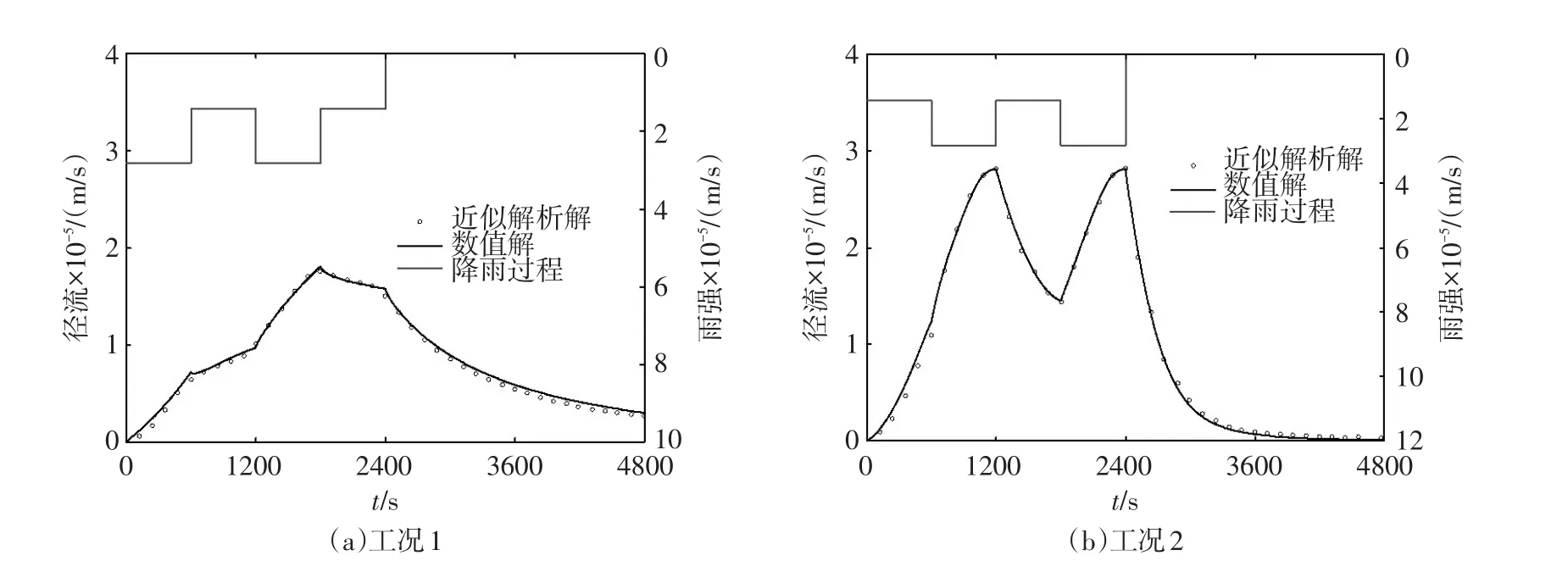
图4 非恒定降雨过程算例计算结果

3.3 二维降雨径流实验算例Cea等［20］在简化的二维流域上进行了降雨径流的室内试验研究，降雨在空间上均匀分布。流域模型由3片不锈钢片组成，三块钢片的坡度均为0.05，流域几何尺寸为2.0 m×2.5 m，在流域内部布置2块条形挡水墙来增加汇流难度，流域的几何尺寸如图5所示。计算选用了两组降雨过程，第一组降雨强度是5.28 mm/min，降雨历时45 s；第二组在前25 s的强度是5.33 mm/min，停止7 s后，重新以5.28 mm/min的强度降雨25 s。计算网格的平均尺寸为0.02 m，计算糙率为0.009。

图6给出了工况1在t=50 s时的流场和水深分布，由图6可以看出，流速最大位置出现在左侧挡水墙末端，水流进入主沟道位置处，这与文献［20］结果一致。图7为本文计算结果与试验测量值及文献［20］计算结果的对比，可以看出，本文计算结果整体上与实验值吻合较好，与文献［20］计算结果也比较接近，工况2中本文数值结果在峰值部分略高于文献［20］的结果，与试验值吻合更好一些。数值计算结果和试验结果的差异有部分原因归因于试验测量手段，比如，降雨喷头从打开到恒定状态有约3～4 s的滞后，这能解释径流的起始阶段，计算值为什么比实测值偏大。另外，降雨试验结束后，喷头无法有效解决漏水问题，所以在退水阶段，模拟的径流过程比实测的径流过程要小一些。

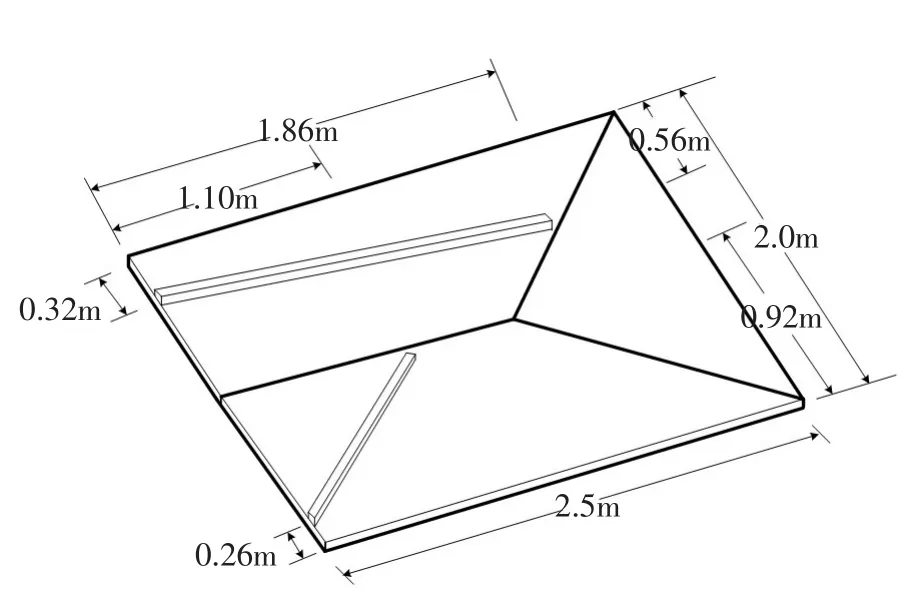
图5 试验流域几何尺寸

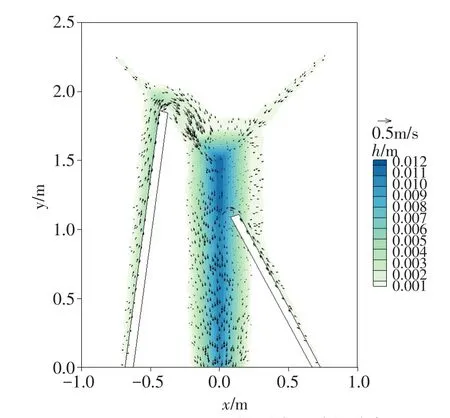
图6 工况1 t=50s时的流场和水深分布

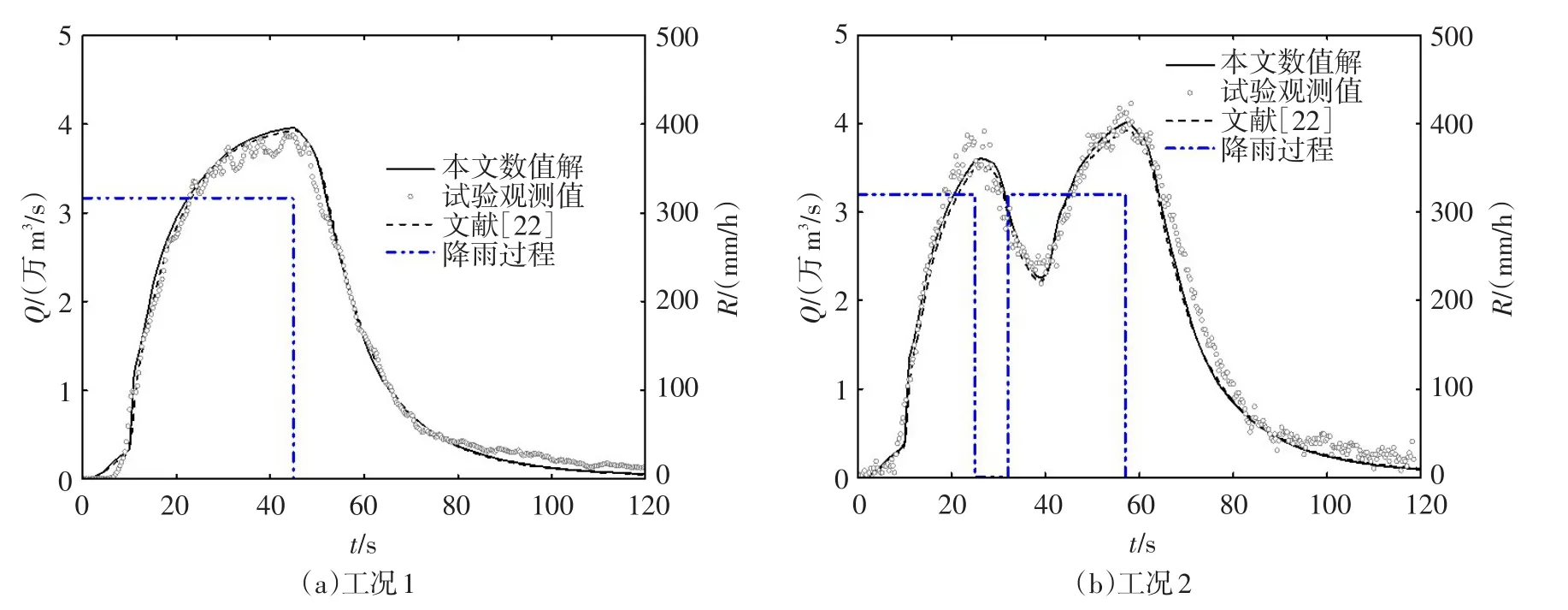
图7 本文计算结果与试验测量值及文献［22］的对比

3.4 变糙率变坡度降雨径流算例该算例为一500 m×400 m的矩形区域内的降雨径流算例［21］，x方向的坡度Sox=0.02+0.0000149x，y方向的坡度Soy=0.05+0.0000116y，降雨过程为一对称的三角形形状，在t=0 min和t=200 min时，雨强r=0，在t=100 min时，雨强r=0.8×10-5m/s。糙率nx=0.1-0.0000168x，ny=0.1-0.0000168y。区域长短边各离散成20段，共生成908个三角形单元，模拟时长240 min。初始条件为整个区域内水深和流速为0，边界条件为x=0和y=0的两条边采用固壁边界，其余两条边为自由出流条件。

图8为本文计算结果与已有文献的数值解对比。由图8可以看出，本文计算结果介于Jaber等［21］和Tsai等［22］的结果之间，整体上与Tsai等［22］的结果更接近一些，而Tsai等［22］的数值解采用了非常细的网格，可以将其结果当作本算例的近似解析解。通过该算例说明本文新研发的模型能够较好地模拟复杂地形和复杂糙率条件下的降雨径流过程。

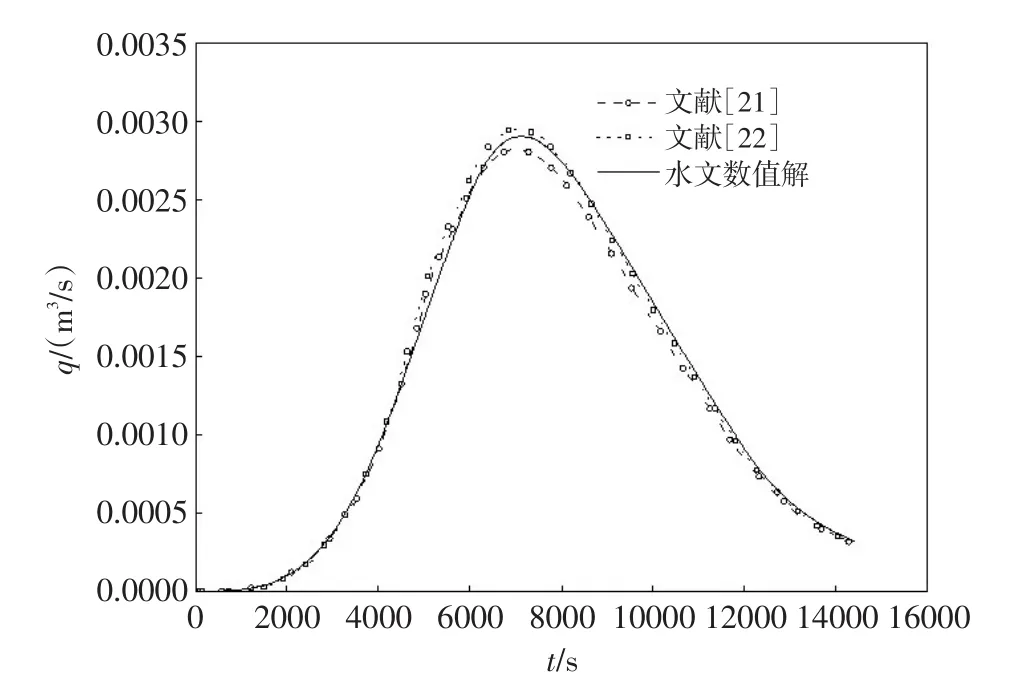
图8 本文计算结果与已有计算结果比较

4 模型应用

4.1 流域概况解家湾流域位于嘉陵江中下游，在四川省遂宁市安居镇境内，紧邻遂宁水土保持试验站。该流域面积 m2，流域平均坡度为0.27，属于典型的丘陵地貌。采用1∶1000的高精度流域测绘数据开展研究工作，地形及水系分布如图9所示。为便于监测流域出口流量过程，在流域末端开挖了一条宽约2 m的集水渠，水渠的末端连接集水池，集水池的出口为三角堰，用来测流。采用平均尺寸2 m的三角形网格离散计算区域，为体现集水渠的效果，在流域末端位置进行了网格加密，该流域总共生成 个三角形网格单元。由于该流域面积较小，地貌均质性较好，以耕地和荒坡为主，林草植被稀少，不失一般性考虑，计算区域内坡面糙率统一取为0.05，沟道糙率取为0.025。为检验该模型处理实际流域的能力，首先对该流域的S曲线进行分析，然后通过一场实测的降雨径流过程对模型的精度进行验证。

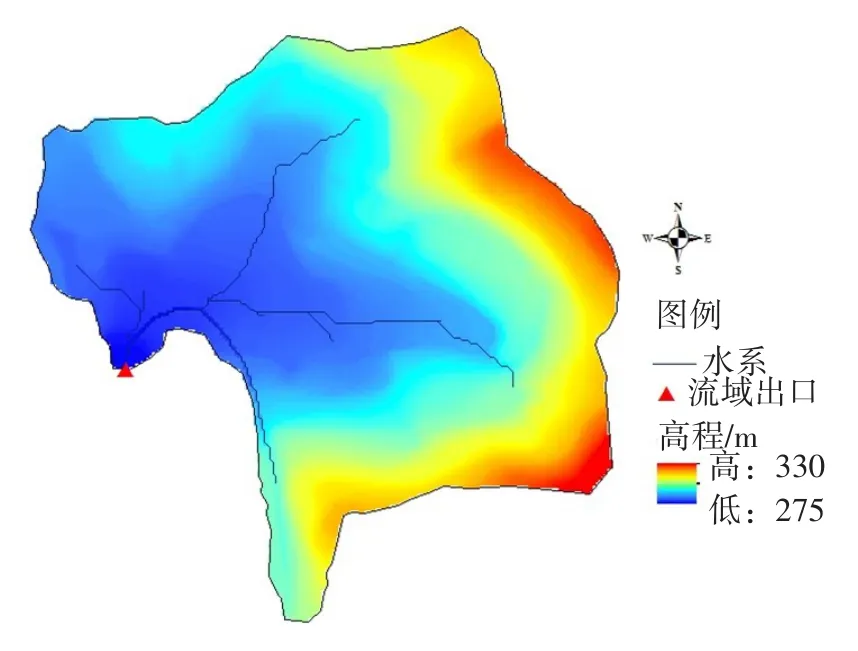
图9 解家湾流域地形及水系分布

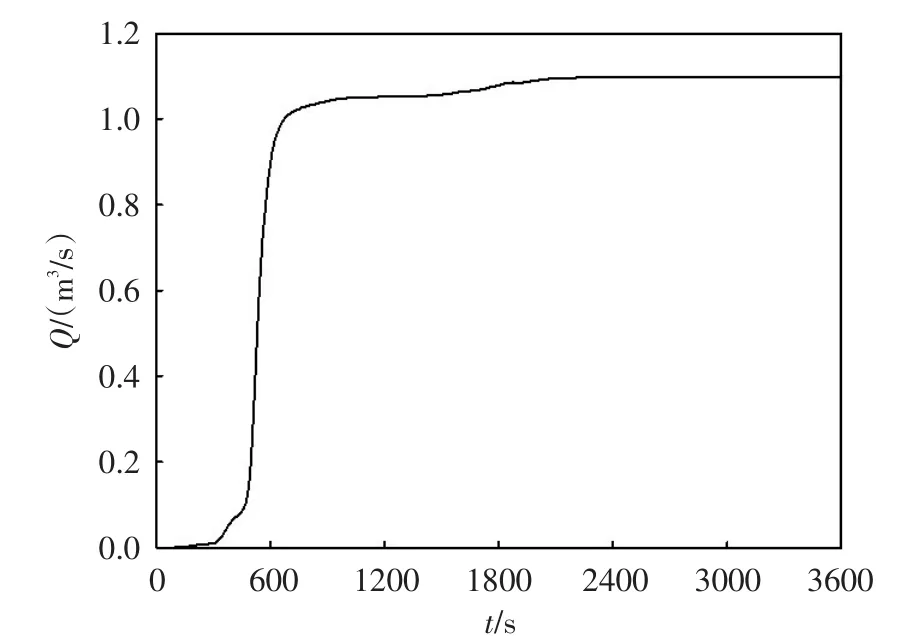
图10 解家湾流域S（t）曲线

4.2 S曲线求解假定时段长为10 min，每个时段的净雨为10 mm，净雨持续不断，则在流域出口形成的流量过程线即S曲线。采用本文模型计算的谢家湾流域的S曲线如图10所示。由图10可以看出，由于流域面积较小，汇流时间较短，所以S曲线在涨水阶段的斜率较陡，S曲线理论上的稳定值为1.097 m3/s，本模型计算的稳定数值解也为1.097 m3/s，说明该模型能够处理实际地形，模型能够保证严格的质量守恒特性。

图11为S曲线达到稳定状态时的水深分布和局部流态。图11（a）中白色区域为水深小于1 cm的区域，流域坡面大部分地区的水深均小于1 cm，流域出口处的人工渠道水深最大，最深处达到1 m左右，除人工渠道外，其余天然沟道的水深相对较小，平均约10 cm左右；图11（b）为A处的局部流场分布，A处为沟道文汇处，流场变化平稳，两条支流汇合后的最大流速约为1.0 m/s左右；图11（c）为B处流场分布，B处为坡面水流进入人工集水渠道处，由于渠道边坡陡峭，所以当水流由渠道边壁进入渠道底部时流速较大，平均流速约为1.3 m/s左右，水流一旦进入渠道底部，由于渠道水深较大，流速降低，平均流速约为0.5 m/s，计算结果与实际情况是吻合的。

图11 S曲线达到稳态时的水深和局部流场分布

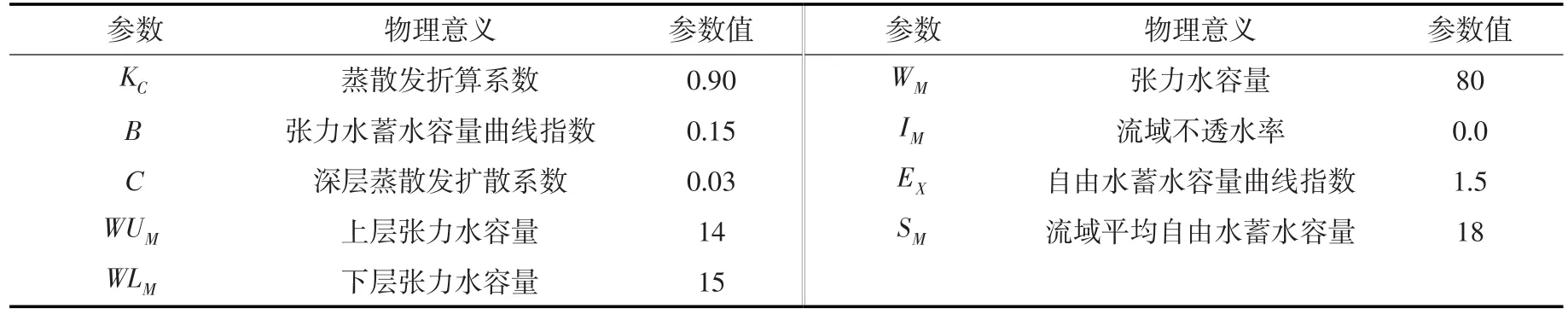
表2 新安江三水源模型产流参数

4.3 实测降雨径流过程模拟采用该流域实测的一场降雨径流过程来验证模型的准确性。该场降雨径流的模拟起始时间为2010年8月21日11点，结束时间为2010年8月22日12点。该流域属于亚热带湿润气候区，采用在我国应用广泛的新安江三水源模型进行净雨过程的计算，采用的产流参数如表2所示。

将坡面净雨过程作为输入条件，采用本文研发的模型进行本场降雨径流过程的模拟，模拟结果如图12所示。由图12可以看出，计算径流过程和实测的径流过程吻合很好，Nash-Sutcliffe系数为0.95。前后两个洪峰的计算值与实测值也比较接近，洪峰出现时间基本吻合。第1个洪峰实测值35.81 l/s，计算值32.30 l/s，相对误差绝对值为9.80%，第2个洪峰实测值65.73 l/s，第2个洪峰计算值61.20 l/s，相对误差绝对值6.89%。按照《水文情报预报规范》（GB/T 22482-2008）的标准，该场洪水的计算精度达到了甲等。

通过以上分析，说明本文研发的二维地表径流水动力模型能够处理实际流域的复杂地形，具有较高的计算精度，模型研发是成功的。

图12 解家湾径流模拟值与实测值对比

5 结论

本文采用Godunov格式对完整的二维浅水方程组进行非结构离散开发完成了一套新的地表径流二维水动力模型。该模型具有如下特点：（1）数值格式具有高分辨率属性，能够自动适应复杂流态变化，克服了运动波或扩散波等简化模型的缺陷；（2）设定地表径流为均匀覆盖流域地表的片状薄层水流，基于该概念完成的模型在干湿处理方面异常简洁，单元水面和地形不需任何特殊处理；（3）采用三角形网格概化流域，地形高程存储在网格节点，对底坡项直接积分求解，地形具有二阶精度；（4）摩阻项采用半隐的处理方法，干湿阈值Htol取为10-10m时，本文中用到的验证算例依然保持了很好的稳定性。

通过4个降雨径流算例对本文模型进行了验证，结果表明，本文的数值解与算例的解析解、实测值或已发表文献结果吻合较好。最后将检验后的模型用于解家湾流域S曲线和场次降雨径流过程的模拟中，结果表明，S曲线稳定阶段的数值解与理论解完全一致；场次洪水计算中，数值解与实测值也符合得很好，说明本文新研发的二维水动力模型应用是成功的。该模型能够为小流域汇流计算提供一种新的途径，可弥补现有水文方法的一些不足。

致谢：Cea博士提供了二维降雨径流实验算例的数据，阚光远博士在解家湾流域产流计算中给予了帮助，在此一并致谢！