超声肿瘤治疗头非线性声场测量方法研究

蒋 剑， 赵 鹏， 王月兵， 郑慧峰

(中国计量大学计量测试工程学院，浙江 杭州 310018)

0 引 言

超声肿瘤治疗头内部的核心部件是聚焦换能器[1]，它将超声波能量汇聚并利用超声波的热效应对人体病变组织进行有针对性的治疗。然而，在频率提高或强度增大时，聚焦换能器极易产生非线性声场[2]，致使释放的声能量难以准确获知，影响治疗效果。因此，对超声肿瘤治疗头的声场进行测量和评价尤为重要。

对声场的测量，出现最早、应用最广泛的是辐射力天平法[3-4]，但由于它自身结构中的吸收靶会吸收掉部分能量，会使测量的准确度降低。2012年，Rajagopal等[5]对量热法进行了深入研究，但其测量效率不高，且选用蓖麻油作为吸收媒介，由于热平衡时间较长，期间会有部分热量散失到测量环境，致使测量值偏低。更重要的是，上述两种方法只能获得声场中单一的功率参数[6]，对于其他声学参数或非线性现象[7]不能进行有效分析，不利于对肿瘤治疗头性能进行全面评价。为解决以上问题，目前多采用水听器法[8]进行声场测量。然而，常用的双水听器法要求两个水听器的间距足够小，其硬件制作困难，使得测量的频率上限一般不会超过10 kHz，故不能应用于非线性声场的测量，且难以保证两个水听器的性能一致，存在着相位不匹配的问题[9]。

针对上述问题，本文依据近场互谱测量原理[10]，仅使用单个探针水听器并选用聚焦换能器作为被测对象，对声场中的声压分布进行测量，通过互谱关系推导出声强和声功率，并展开一系列误差分析，验证了近场互谱法适用于超声肿瘤治疗头非线性声场的测量。该方法不仅可以获得多个声学参数，能够对治疗头的性能作全面评价，而且能够克服双水听器法测量频率上限低以及测量系统相位不匹配的缺点。

1 基本理论

1.1 声强与声功率

由声学理论可知，声强可用单位时间内、单位面积的声波向前进方向毗邻媒介所做的功来表示，如下式[11]所示：

式中：I——声强；

T——平均时间；

Re——取实部；

p——瞬时声压；

v——瞬时振动速度。

通过声强对面积的积分，可计算出某曲面S上的声功率[12]，表示为

其中，当S为封闭曲面时，W表示曲面内声源向介质中辐射的声功率；s表示被测面的面积；In表示声强。

1.2 声强测量原理

根据式（1）可知，倘若测得声压与振速，求两者之积便可得到声强值，但是在实际测量中，直接测量质点振速极其困难[13]。利用双测量平面可以较好地解决这个问题，依据Euler方程，可求出声压与质点振速的关系式[14]：

式中ρ表示介质密度。如图1所示，设沿着r方向上相距Δr的a、b两点处的声压值分别为Pa和Pb，ab连线的中点处声压值为Po，当满足以下关系时：

式中λ为波长。对式（3）取一阶有限差分，可得：

由此，o点的振速可以通过其两侧距离很近的两点声压计算得到。用a、b两处的平均声压代替o点处的声压：

将式（5）和式（6）代入式（1），可得o点声强：

依据声强与两点声压的互谱关系[15]，推导可得：

式中：ω=2πf——圆频率；

Gab(ω)——两点声压互功率谱；

Im——取虚部。

图1 声强测量原理示意图

1.3 近场互谱测量法

如图2所示，采用单个水听器在聚焦声场的预聚焦区域选取两个相距很近的平面A、B进行声压扫描测量，通过式（8）计算得到O平面上的声强分布。

图2 近场互谱测量法示意图

在实际测量时，测量面S被划分成N个小面元Δsi(i=1,2,3,···,N)，将式（2）转换成离散形式后，辐射声功率W可近似表示为

式中Ii为第i块小面元上的法向声强值。

2 实验研究

2.1 测量实验

搭建实验系统，如图3所示，硬件部分主要包括信号发生器、功率放大器、聚焦换能器、水听器、前置放大器、数据采集系统、运动控制系统、计算机等。实验过程如下：

1）信号发生器发射一个脉冲信号，一方面经过功率放大器放大并驱动聚焦换能器工作；另一方面被采集卡直接采集，作为参考信号，后期用来捕获初始声压值和计算时延。

图3 测量系统示意图

2）超声波在除气水介质中传播，被水听器所接收，水听器输出的电信号经过前置放大器，由数据采集系统采集并存储在计算机中。

3）计算机通过运动控制系统控制水听器在水箱中做三维运动，对某一被测位置的前后两个平面进行声场扫描，从而获得声压数据。

取声场中3个不同位置进行测量实验，选用直径为20 mm，工作频率为2 MHz的聚焦换能器作为被测对象。水听器选用ONDA公司的仓式水听器，其灵敏度已校准。在确定焦点位置后，再选取距离焦点前后各10 mm的两个被测位置，采用近场互谱测量法，对每个位置测量两个平面，依据式（4），取两个测量平面的距离为0.1 mm。为了保证大部分能量集中在测量平面内且提高测量效率，选取焦点处的测量平面大小为6 mm×6 mm，水听器的扫描步长为0.1 mm，而两侧位置的测量平面大小为12 mm×12 mm，水听器扫描步长为0.2 mm。

2.2 实验结果与误差分析

分别对聚焦换能器焦点前10 mm处、焦点处和焦点后10 mm处3个测量位置进行了声压分布测量。由于聚焦换能器能够将声能量聚集在很小区域内，当其辐射声波的频率较高或能量较大时，声波在传播时波峰质点振动速度会大于波谷，使得声波的波形发生畸变，声波的能量转向更高的频率成分，从而形成非线性声场。此时，可通过声压推算出3个测量面上各次谐波的声强分布，如图4、图5和图6所示。

图4 焦点前10 mm处平面内各次谐波声强分布

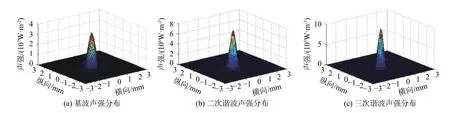
图5 焦点处平面内各次谐波声强分布

图6 焦点后10 mm处平面内各次谐波声强分布

从声强分布图中可以看出，非焦点处的声强皆小于焦点处的声强，且焦点前的非线性现象弱于焦点后，这是因为波形的畸变是随距离增加而逐渐累积的，波的传播距离愈大，波形的畸变就愈严重，同时测量的结果符合声波在传播过程中的衰减规律。此分布图可以用来评价聚焦换能器的聚焦效果。

为了更加全面地评价肿瘤治疗头的性能，计算出各个测量面的声功率值，以获得更多的超声肿瘤治疗头性能评判指标。已知声强分布，通过式（9）计算3个位置的声功率值，结果如表1所示，同时得出3个位置的声功率一致性误差小于5%，说明测量方法是可行的。

表1 3个不同位置的声功率

一致性误差产生的主要原因是测量系统的偏差，为了检验测量系统的误差大小，对上述实验中焦点前10 mm位置的声功率进行了6次重复性测量实验，计算出该位置声功率测量的重复性误差在2%以内，说明本文所述的近场互谱法具有良好的重复性，也表明测量系统的精度符合要求。为了进一步验证测量结果的正确性，将上述测量结果与辐射力天平法的测量结果进行比对。使用进口的UPM-DT-1PA毫瓦级超声功率计，采用控制变量法，对实验中所用的聚焦超声换能器进行声功率测量，测出焦点处的声功率值为5.662 W，由于辐射力天平法可以向NIST溯源，可将5.662 W作为上述聚焦换能器焦点处的理论真值。根据相对误差的计算公式：

式中δ为相对误差；Δ为绝对误差；L为理论真值。计算可得上述3个测量位置的声功率相对误差，结果如表2所示。

表2 3个不同位置声功率的相对误差

由表可知，3个位置的测量相对误差都小于5%，与辐射力天平法的比对结果十分理想，表明近场互谱测量法对聚焦换能器非线性声场的测量结果是可靠的。在实际治疗过程中，超声肿瘤治疗头焦点处的声能量大小是人们最为关心的。从图5可见，当治疗头产生非线性声场后，在焦点处的基波声强值最大，但由于非线性导致了多次谐波的产生，会加剧焦点处的热效应，倘若热效应太强，则会损伤周围正常组织。采用本文所述的方法进行声场测量，可将非线性导致的各次谐波声强分布都直观地展现出来，为超声肿瘤治疗头的性能评价提供了依据。

3 结束语

本文采用近场互谱测量法，利用单个水听器对聚焦换能器非线性声场中3个不同位置的声压、声强和声功率进行了测量与计算。不仅克服了以往的测量方法仅能获得单一功率指标的不足，而且验证了该方法对非线性声场测量的可行性，更利于全面评价超声肿瘤治疗头的性能。

值得注意的是，仅使用单个水听器进行声场测量，消除了双水听器法相位不匹配的问题，提高了测量精度，也提高了测量频率上限，使其达到兆赫兹的级别。然而，由于非线性导致了多次谐波的产生，就要求水听器能够拥有足够的带宽，否则会影响测量结果的准确性，因此，高性能水听器的研发势在必行。