基于GM(1,1)和人工蜂群的配电测试系统状态估计

符金伟， 关石磊， 左思然， 范闻博， 王中宇

(1. 中国电力科学研究院配电研究所，北京 100085; 2. 北京航空航天大学仪器科学与光电工程学院，北京 100191)

0 引 言

配电测试系统状态估计方法是一种利用测试系统中量测数据的相关性和冗余度，对运行参数和运行状态进行预测和估计，为其他电力控制设备提供完整、可靠、高精度实时数据的方法[1]。

常用的状态估计方法有加权最小二乘法、等效功率变换法、基于支路估计法等。加权最小二乘法将量测值与其估计值之差的平方和作为目标函数，具有模型简单、收敛性好等优点，但是该方法也存在运算量大、抗差能力弱等问题[2]。等效功率变换法将支路功率、电压幅值和电流幅值转换为支路两端等效功率，该方法具有计算速度快、内存占用少的优点，但是不易处理注入型的量测量[3]。支路估计法将整个配电网的状态估计问题分解为与对应支路数相等的状态估计子问题。该方法与潮流计算的前推回代相类似，计算速度快，但是根节点电压的正确性对计算结果的影响很大，一般只用于辐射网[4-5]。

人工蜂群算法由Karaboga提出，其目的是解决多变量函数的优化问题。该算法利用雇佣蜂、侦察蜂和跟随蜂3种具有不同功能的蜂群采集并寻找最优蜜源[6]。在蜜蜂个体局部寻优的基础上，通过比较适应度函数确定全局最优解[7]。人工蜂群算法的鲁棒性强并且具有较好的寻优质量，因此被广泛应用于配电网网络重构、求解电力系统最优潮流模型和配电网状态估计等方面。但是，人工蜂群算法运用于状态估计时，存在节点状态估计准确度不稳定，容易陷入局部最优解等问题。分析其主要原因在于，量测数据在测量和传送过程中存在着偶然故障和随机干扰，因此配电测试系统的量测数据中存在着不良数据，这些不良数据造成了状态估计准确度的恶化。

GM(1,1)模型是灰色理论最基本的一种预测模型，它通过原始量测数据的预处理和灰色模型的建立，对数据序列进行外推[8]。对原始量测序列进行灰色生成，能够使非负序列或摆动序列转化为非减序列，从而削弱量测数据的随机性，突出量测数据的内在规律性，有效判别序列中是否存在不良数据。

本文提出基于GM(1,1)的不良数据修正方法，减少不良数据对状态估计误差的影响。在现有的人工蜂群算法基础上采用Metropolis准则[9]进行迭代终止判定，从而避免陷入局部最优解，提升算法的全局搜索能力。

1 状态估计模型

1.1 目标函数

配电测试系统实时量测是对装设在馈线上的测量装置进行实时收集，包括节点电压幅值、支路有功功率和无功功率、节点注入有功功率和无功功率等。量测量z可以表示为

式中：h(x)——量测函数；

e——量测过程中引入的随机误差；

当J(x)达到最小值时，得到加权最小二乘法的估计结果。

1.2 等式约束和不等式约束

对配电测试系统进行状态估计时，需要满足等式约束和不等式约束条件[10]。等式约束条件基于基尔霍夫第一定律，目标函数的求解值必须满足一组约束条件。

不等式约束条件有负荷有功、负荷无功、节点电压约束，可表示为

式中：PLD——负荷有功功率，W；

QLD——负荷无功功率，W；

V——除起点外的所有节点电压的幅值，V；

k——负荷节点数；

s——所有节点数。

2 不良数据修正

通常，配电测试系统量测数据分为有效量测数据和量测噪声两部分。由于粗差的出现，实际噪声分布与假设的量测噪声分布模型存在偏移，因此不良数据是影响状态估计结果准确性的关键因素[11]。传统的不良数据辨识方法有标准残差法、零残差法和非二次准则法等，但是这些方法均无法消除残差污染和残差淹没，进一步会造成不良数据的误判和漏检[12]。为了克服残差污染和残差淹没现象，引入GM(1,1)模型实现对不良数据的修正。

以根节点电压幅值V为例，选择一定的时间窗口，读取量测值。令多组原始量测值按从小到大排序，其序列记为V(0)。对序列V(0)做累加生成，得到测量值累加数列V(1)：

式(4)的累加曲线可以用一个折线来包络，包络线的下界的折线方程为

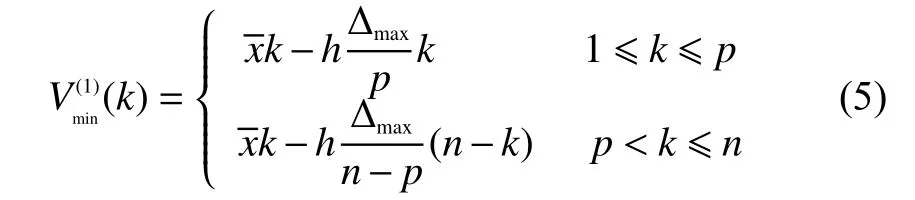
其中h一般取3.75。

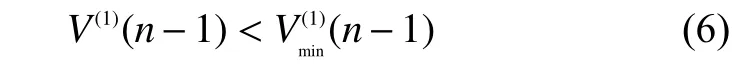
对于量测值序列如果满足式(6)，则认定量测值中有不良数据，V(0)(n-1)和V(0)(n)可剔除；否则，最大量测值是否为不良数据无法判定。因此需要为数据V(1)建立GM(1,1)模型获得一个预测值V(1)(n+1)。GM(1,1)灰色微分方程为

式中：a——GM(1,1)的发展系数；

b——GM(1,1)的灰作用量。

式中：z(1)——V(1)的均值序列；

V(1)——V(0)的一次累加序列。

通过求解灰色微分方程可以得到预测值(1)(n+1)，表达式为

其中k=1,2,···,n。

为了保证每个节点量测数据的个数不变，采用线性插值法对不良数据进行修正，即不良数据的修正值采用其前后两次测量值的均值。

3 配电测试系统状态估计

有将负荷有功功率和无功功率作为状态变量：

式中：P——负荷有功功率，W；

Q——负荷无功功率，W。

则量测函数表达式为

式中：V——节点电压幅值的量测值，V；

I——节点电流幅值的量测值，A。

配电测试系统状态估计就是对1.1节中提出的目标函数进行优化求解。采用改进的人工蜂群算法对其进行求解，步骤如下：

1)种群初始化

输入初始参数，包括蜂群的规模M、雇佣蜂的规模S和最大迭代次数MAX，并将局部搜索限度trail置零。

随机生成S个状态向量，则产生可行解的公式为

其中τ1、τ2为0～1之间的随机数。

将蜜源设置为目标函数J(x)，计算各个状态向量对蜜源的适应度fit(x)。

2)雇佣蜂阶段

雇佣蜂在蜜源的邻域进行随机搜索，表达式为

其中τ3、τ4为0～1之间的随机数。

计算当前状态量对蜜源的适应度fit(xi′)，比较fit(xi)与fit(xi′)的大小。若fit(xi′)＞fit(xi)则状态量更新为xi′；否则保持原状态量xi不变。同时将trail(i)加1，若trail(i)=trail则雇佣蜂变为侦察蜂并放弃该解，进入步骤4)；否则执行步骤3)。

3)跟随蜂阶段

跟随蜂以一定的概率选择状态量，概率计算的表达式为

在其附近进行随机搜索，搜索方式与步骤2)中的雇佣蜂相同。若fit(xi′)＞fit(xi)则状态量更新为xi′，跟随蜂代替雇佣蜂的位置；否则保持xi不变。

4)侦察蜂阶段

令trail(i)=0，侦察蜂根据式(14)随机生成新的状态量xi′。当fit(xi′)＞fit(xi)时更新状态量为xi′，侦察蜂变为雇佣蜂；否则保持不变。

5)迭代终止判定

每一次迭代后，若最优解的适应度函数增大，那么就接受它；否则按照下式来判断是否接受：

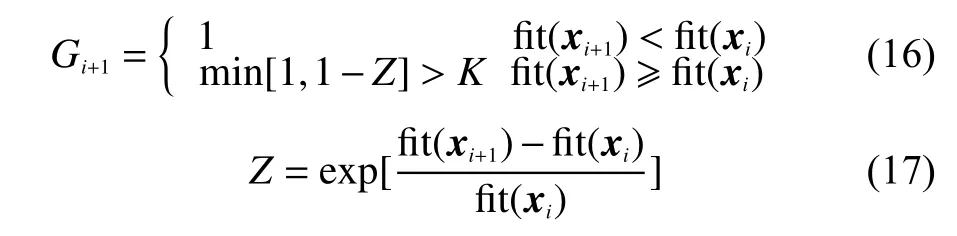
式中：K——0～1之间的判定阈值，通常取0.5；

G(xi+1)——状态xi+1下的接受概率。

xi+1可以表示为

其中α为温度冷却系数。

令总循环次数加1，判断是否达到迭代终止条件，如果是则终止迭代并输出最优解；否则重新返回步骤2)。

6)记录当前的最优解。

4 实验分析

为了对本文提出的方法进行验证，采用由中国电力科学研究院搭建的33节点配电测试系统开展实验，其接线图如图1所示。分别在节点4、8、12、15、21、23、28和31上配置配电自动化终端和分布式电源。

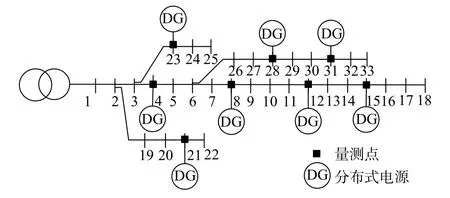
图1 33节点配电测试系统接线图

采用GM(1,1)方法分别对8个节点的电压幅值和电流幅值进行不良数据检测，得到节点4中第18次量测数据、节点12中第11次量测数据以及节点28中第6次量测数据为不良数据，如图2和图3中的红色叉号所示。

图2 节点电压幅值

图3 节点电流幅值

采用线性插值的方法对检测到的不良数据进行修正，即计算出不良数据的前后各一次量测值的平均值，将其作为节点当次量测的修正值[13]。各节点的不良数据的修正结果如表1所示。

表1 不良数据修正

完成不良数据的检测与修正后，采用改进的人工蜂群算法进行配电网状态估计。设定蜂群的规模为50，雇佣蜂的规模为25，局部搜索限度为6，最大迭代次数为300。设定随机数τ1和τ2的值为0.5，随机数τ3和τ4的值为0.3，温度冷却系数α的值为1.5。同时，根据原始量测数据，分别采用加权最小二乘法和人工蜂群算法进行状态估计。表2和表3分别表示采用不同方法下有功功率和无功功率的估计结果。

对8个节点的负荷有功功率和无功功率进行估计时，不同方法的估计误差绝对值如图4和图5所示。通过各节点估计误差绝对值的比较发现，加权最小二乘法的误差最大，其次是人工蜂群算法，而本文方法的误差最小。另外，对存在不良数据的节点4、12和28进行分析后可以发现，相对于加权最小二乘法和人工蜂群算法，本文方法的估计误差绝对值的波动范围最小。

表2 负荷有功功率估计结果比较

表3 负荷无功功率估计结果比较

图4 有功功率估计误差绝对值比较

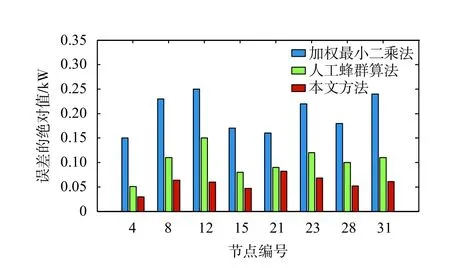
图5 无功功率估计误差绝对值比较

同时，采用不同方法对选取的8个节点重复进行15次状态估计，记录运行时间，得到8节点状态估计的平均运行时间如表4所示。

表4 不同方法的平均运行时间比较

由表可知，加权最小二乘法的复杂度低，因此该算法的平均运行时间最短；人工蜂群算法在存在不良数据时对全局最优值的搜索效率不高，平均运行时间最长。本文方法的平均运行时间与加权最小二乘法的相接近，同时比人工蜂群算法减少了46%。

为了对这3种状态估计方法的误差进行比较，定义平均绝对误差MAE和节点最大相对误差NMRE：

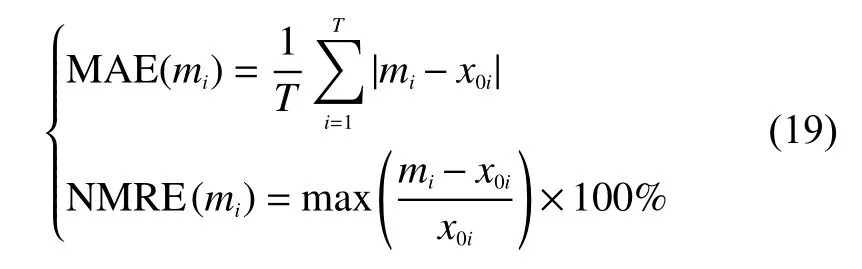
式中：mi——i时刻状态量的估计值；

xi——状态量的真值；

T——节点数目。

根据式(19)计算出不同方法估计有功功率和无功功率时的MAE和NMRE，结果如表5所示。

表5 不同方法估计误差比较

由表可知，本文方法估计的有功功率MAE比加权最小二乘算法和人工蜂群算法的相应结果分别减少了大约69%和43%，NMRE分别减少了70%和63%；对于无功功率，本文方法比加权最小二乘算法和人工蜂群算法的MAE结果分别减少了大约60%和33%，NMRE分别减少了58%和57%；这说明本文方法对于每一节点的状态估计误差都明显小于加权最小二乘法和人工蜂群算法，验证了本文方法的有效性。

5 结束语

1)本文提出了一种基于灰色累加生成和人工蜂群算法的配电测试系统状态估计方法。通过建立灰色微分方程求解序列预测值来判断序列中是否存在不良数据，能够解决传统方法中存在的残差污染和残差淹没问题。

2)研究了人工蜂群算法的节点状态估计准确度不稳定、容易陷入局部最优解等问题。首先采用线性线性插值的方法对不良数据进行修正，其次建立迭代终止判定条件，提高算法的全局最优搜索能力。在存在不良数据的条件下，本文方法比人工蜂群算法的估计精度更高，运行时间更短。

3)本文对不良数据的修正采用了线性插值的方法，当量测数据的采样频率较低时状态估计准确度会受到影响。因此可以作为下一步的研究方向。