论流体压力形式的统一性和内涵多样化
聂千越 聂千翔
(⒈ 青岛西海岸新区第一高级中学 266555;⒉ 山东省日照第一中学(东校) 276826)
物理学习中要面对许多复杂的公式推导与数值计算,难免让人产生难懂之感.实际上,物理学是充满美感的,统一美便是其美感的一个典型特征.“窥一斑而知全豹”,本文以重力场静止流体和直线匀加速运动相对静止流体为研究对象,研究流体压力的分布的一般规律,探讨流体压力形式的统一性和物理参数内涵的多样化.
一、重力场静止流体的压力
重力场是典型的质量力场,地球上的一切物质都处于重力场中.工程中的许多问题,诸如液体容器的受力、船舶浮力和浮力矩设计、液压机械的受力等,都与重力场中静止液体的力学行为有关.
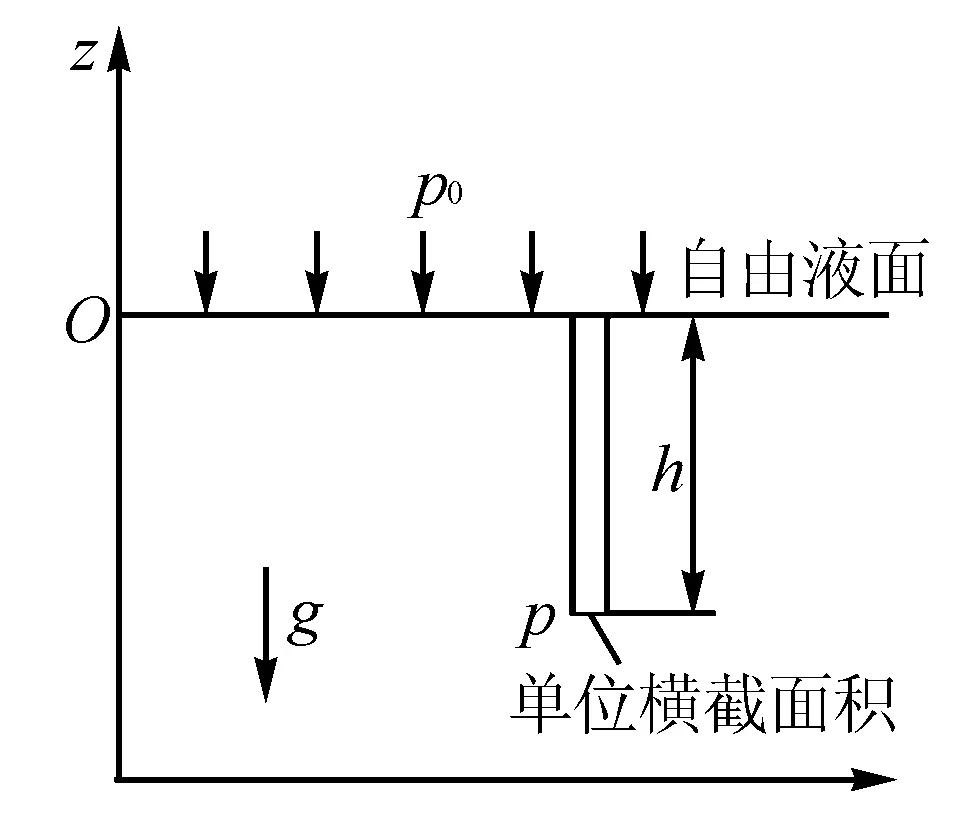
图1 重力场的静止液体
重力场静止流体单位质量力f=g.对于图1所示的坐标系统,单位质量力的分量表达形式为
静力学全微分方程为
dp=ρ(fxdx+fydy+fzdz)
(2)
将式(1)代入式(2)中,得到重力场静止流体的压力微分方程,即
dp=-ρgdz
(3)
对于不可压缩流体,ρ为常数,自由液面承受外界大气压p0,所以边界条件为p|>z=0=p0,对式(3)进行积分,可得
p=p0-ρgz
(4)
若用距离自由液面的深度h替代-z,压力则有更一般的表达形式
p=p0+ρgh
(5)
二、直线匀加速运动相对静止流体的压力
根据达朗贝尔原理,质量为m的物体以加速度a运动时要受到与加速度反方向的惯性力作用,惯性力为-ma,并且惯性力与物体所受其他外力构成平衡力系.因此,对于重力场中以加速度a运动的流体,其单位质量力为
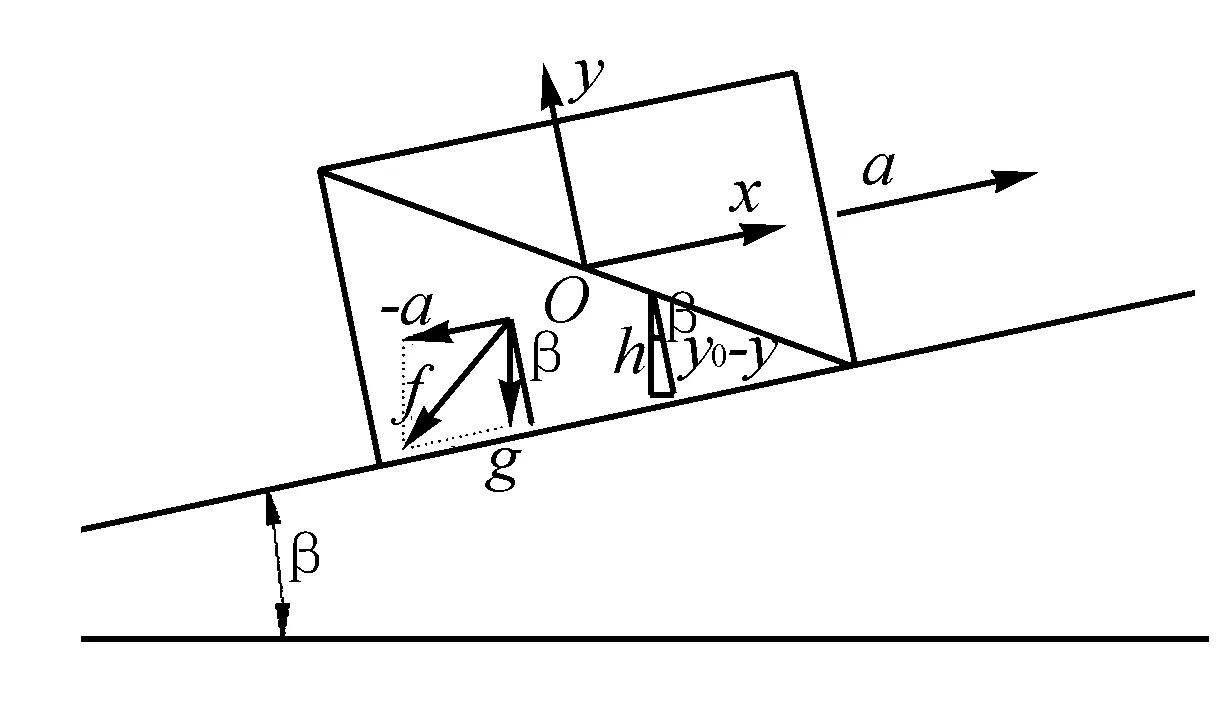
图2 直线匀加速运动容器
f=-a+g
(6)
图2所示容器以等加速度a沿升角β的斜面做直线运动.设液体密度为ρ,自由液面的压力为p0,液体所受的
单位质量力为
fx=-ax+gx=-(gsinβ+a)
fy=-ay+gy=-gcosβ
fz=-az+gz=0
(7)
将式(7)代入式(2)中,可得容器中相对静止流体的压力全微分方程为
dp=-ρ(gsinβ+a)dx-ρgcosβdy
(8)
考虑边界条件p|>x=0,y=0=p0,对式(8)积分,可得
p=p0-ρ(gsinβ+a)x-ρgcosβy
对于式(8),若令dp=0,积分可得自由液面方程,即
将式(10)代入式(9)中,可得
p=p0+ρg(y0-y)cosβ
(11)
由图2可知(y0-y)cosβ为研究点距离自由液面的竖直深度h,若令(y0-y)cosβ=h,则式(11)亦可写成
p=p0+ρgh
(12)
通过计算和适当的变换,重力场静止流体和直线匀加速运动相对静止流体的压力均可表达为p=p0+ρgh,但p0和h在不同场合其物理含义也有所不同.p0是自由液面的压力,也就是外界的大气压力.深度h均指研究点到自由液面的竖直距离,但表达形式不同,具体公式文中已列出.

