基于极限学习机的边坡可靠度分析

，,3，，，

(1.中国科学院水利部成都山地灾害与环境研究所 山地灾害与地表过程重点实验室，成都 610041；2.中国科学院大学，北京 100049; 3.中国科学院 青藏高原地球科学卓越创新中心，北京 100101)

1 研究背景

目前对边坡稳定性的研究，广泛采用安全系数法。该法把岩土的参数值取为定值，通过求解安全系数来判断边坡稳定情况，是一种确定性的计算方法。但实际边坡工程存在大量不确定性，包括各种计算参数的随机性和变异性[1]，仅以安全系数的大小来判断边坡安全性是远远不够的。为了弥补传统稳定性分析方法的缺点，引入了可靠度理论。可靠度理论运用概率论和数理统计方法将各种不确定因素看作随机变量来分析边坡失稳的可能性[2]，能够更合理地反映边坡的实际安全状况。

可靠度是指结构在规定时间和条件下，完成预定功能的概率，常用可靠度指标来衡量；不能完成预定功能的概率称为失效概率[3]。可靠度指标越大，失效概率则越小。边坡可靠度的研究方法很多，如：一次二阶矩法(中心点法[4]、验算点法)、响应面法、蒙特卡罗法等。其中，中心点法精度较低;验算点法简单、准确，但只适用于目标功能函数能够显式表达的边坡。基于二次多项式的常规响应面法，只保证验算点附近的拟合精度[5-6]，有时还存在收敛困难的问题。直接蒙特卡罗法的精度较高但计算量偏大[7]。基于此，很多学者将智能算法引入可靠度分析，利用智能算法强大的数据拟合功能构造响应面函数。目前应用较多的是BP神经网络[8]和支持向量机[9]等，不过BP神经网络需要人为设置大量参数，且易陷入局部极小值；支持向量机参数确定困难，且需消耗较多时间进行参数调整和训练[10]。

极限学习机是一种新的单隐含层前馈型神经网络方法，该法在训练过程中无需调整输入层与隐含层间的权值以及隐含层神经元的阈值，只需设置隐含层神经元的个数，便可获得唯一最优解。因此，与传统方法相比，其学习速度快、泛化性能好[11]，受到越来越多的关注[12]。基于此，本文将极限学习机引入边坡可靠度分析，利用均匀试验和FLAC3D强度折减法生成训练样本，通过极限学习机建立随机变量与安全系数之间的映射关系，构建响应面功能函数，结合蒙特卡罗模拟求解边坡的失效概率和可靠度指标。算例分析表明，该方法可行，具有较好的应用前景。

2 基于FLAC3D和极限学习机的可靠度分析

2.1 FLAC3D强度折减法

强度折减法中将边坡安全系数定义为：对岩土体抗剪强度进行折减时，边坡刚好达到临界破坏状态的折减程度，即岩土体实际抗剪强度与临界破坏时剪切强度的比值[13]。拆减后的黏聚力和摩擦角公式如下：

cF=c/Ftrial；

(1)

φF=arctan(tanφ/Ftrial) 。

(2)

式中：cF为折减后的黏聚力；φF为折减后的摩擦角；Ftrial为折减系数。

FLAC3D在计算安全系数时，用Solve FOS命令求解，通过不断增大强度折减系数，反复调整岩土体的强度指标c和φ来分析边坡稳定性，直至达到临界破坏，此时强度折减系数即为安全系数。与极限平衡法相比，该方法无需假定滑动面位置、形状，避免了极限平衡法中各种人为假定的缺点[14]，且能反映岩土体材料应力、变形等信息。

2.2 极限学习机

2.2.1 极限学习机简介

极限学习机(Extreme Learning Machine, ELM)是Huang等[15-16]于2004年提出的一种新的单隐含层前馈型神经网络方法，包括输入层、隐含层和输出层，其中输入层与隐含层、隐含层与输出层神经元间为全连接。

给定Q个不同样本的集合R，其表达式R={(xi,yi)|i=1,2,…,Q;xi∈Rn,yi∈Rm}，则具有l个隐含层神经元的ELM输出tj,可表示为

(3)

式中：wi为输入神经元与第i个隐含层神经元间的连接权值；βi为第i个隐含层神经元与输出神经元间的连接权值；bi为第i个隐含层神经元的阈值；xj为第j个样本的输入值；g(x)为隐含层神经元的激活函数。式(3)可表示为

Hβ=T。

(4)

式中:β=[β1β2…βl]T，T=[t1t2…tQ]T;H为隐含层的输出矩阵，具体表达式为

H(w1,w2,…,wl,b1,b2,…,bl,x1,x2,…,xQ)=

(5)

单隐含层神经网络学习的目标是使输出的误差最小，即网络可以零误差逼近Q个训练样本，表达式为

(6)

然而，当激活函数g(x)无限可微时，网络参数并不需要全部进行调整，w和b在训练前可随机选择，且在训练过程中保持不变。而输出连接权值β可通过求解以下线性方程组的最小二乘解来获得,即

(8)

其解为

(9)

式中H+为隐含层输出矩阵H的Moore-Penrose广义逆。

2.2.2 极限学习机的训练与检验

在ELM训练时，需先将样本数据归一化为[-1,1]之间的数，可利用MatLab软件的mapminmax函数进行处理。

隐含层神经元数对ELM的性能影响较大，一般采用“试凑法”进行选择。本文从3开始依次增加隐含层神经元数，逐个比较网络的性能，来确定最佳神经元数。对网络泛化性能的评价，通常是通过仿真误差err、决定系数R2等参数进行的[10]，公式如下：

(10)

(11)

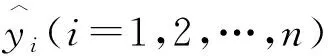
2.3 蒙特卡罗模拟

当影响边坡稳定性的各个基本变量Xi的概率分布函数已知时，利用计算机产生符合相应基本变量概率分布的N组随机数(N足够大)，分别代入极限状态方程Z=K-1(K=f(x1,x2,…,xN)为极限学习机拟合的响应面函数)，若其中有M个<0，由伯努利大数定理可知，失效概率为

Pf=P{Z<0}=P{f(x1,x2,…,xN)<1}=M/N。

(12)

对这N个Z1,Z2,…,ZN，其均值μZ和均方差σZ的估计量分别为：

(13)

(14)

可靠度指标为

(15)

当基本变量为正态分布时，可由式(16)求解对应的可靠度指标。

β=-Φ-1(Pf)=Φ-1(1-Pf) 。

(16)

2.4 基于极限学习机的可靠度分析步骤

对于边坡极限功能函数无法显式表达的情况，可利用极限学习机强大的数据拟合功能，建立安全系数与随机变量间的复杂非线性关系，构造出极限状态方程，然后利用蒙特卡罗模拟求解可靠度指标，具体步骤为：

(1)确定影响边坡稳定性的因素及其概率分布，利用均匀试验和FLAC3D软件，构造出极限学习机的训练和检验样本。

(2)选择合适的隐含层神经元数，利用上述样本，通过极限学习机建立安全系数与随机变量之间的映射关系，即响应面函数。

(3)将蒙特卡罗模拟生成的大量随机变量数据，代入到训练好的极限学习机中，获得相应安全系数，进而求解边坡失效概率和可靠度指标。

3 算例分析

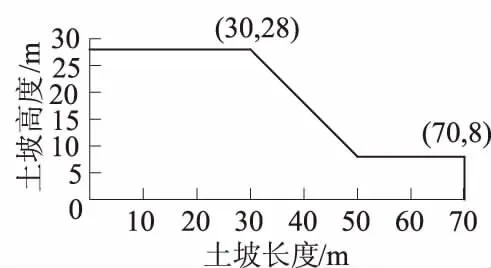
图1 边坡剖面Fig.1 Cross-section of slope

采用如图1所示的均质边坡[17]，坡比为1∶1，坡高H=28 m。土层参数：黏聚力c=40 kPa，内摩擦角φ=20°，剪胀角ψ=20°，重度γ=20 kN/m3，杨氏弹性模量E=20 MPa，泊松比ν=0.3。其中c和φ为相互独立的正态随机变量，变异系数δ均为0.1，其余参数为定值。

3.1 边坡安全系数求解

边坡土体采用摩尔-库伦理想弹塑性模型，底部为刚性边界，上部为自由边界，左右两侧垂直边界为水平滑动支承。坡体等效为平面应变问题，将y方向设为一个单位宽度。采用六面块体网格将边坡模型划分为1 346个节点，610个单元。

随机变量c和φ取均值时，利用FLAC3D强度折减法分析边坡稳定性，得到安全系数为1.29，边坡剪切滑移面如图2所示。同时，利用Bishop法、Spencer法、Morgenstern-Price法进行了分析计算，安全系数分别为1.270，1.269，1.267。文献[14]和文献[17]中利用ANSYS软件求得此坡安全系数分别为1.25，1.29，利用滑面应力法求得安全系数为1.320，均与本文方法结果相近。

图2 边坡剪切应变增量及速度矢量Fig.2 Shear strain increment and velocity vectors of slope

3.2 训练样本和检验样本数据的生成

本文采用均匀设计[18-19]生成样本数据，该法生成的试验点在高维空间内均匀分散，有限的数据便能具有广泛的代表性，可大幅减少试验次数。样本数据的生成采用现成的均匀表进行。

由于c和φ服从正态分布，取值范围可通过[μ-3σ,μ+3σ]确定，故c取值范围为[28,52]kPa，φ为[14°,26°]。根据上下限利用插值法，将第1列和第5列数据分别转化为c和φ真实范围内的数值，然后通过FLAC3D软件逐组求解安全系数，作为网络的训练样本，如表1所示。

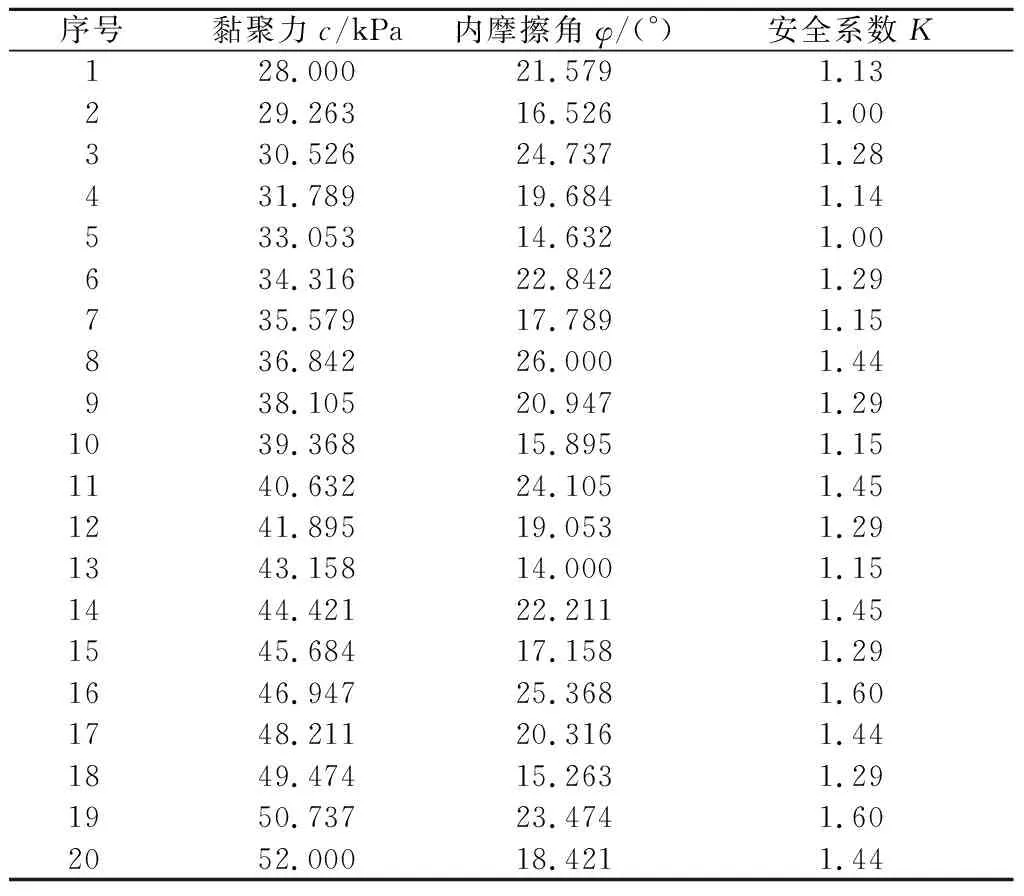
表1 极限学习机的训练样本Table 1 Training samples of ELM

表2 极限学习机的检验样本Table 2 Test samples of ELM

3.3 ELM预测模型的训练与检验

经过比较，激活函数为Sigmoidal时预测精度相对较高。为减小随机初始权值w和阈值b对结果的影响，对每个神经元数分别运行10次，得到隐含层神经元数与ELM性能间的关系，如图3所示。

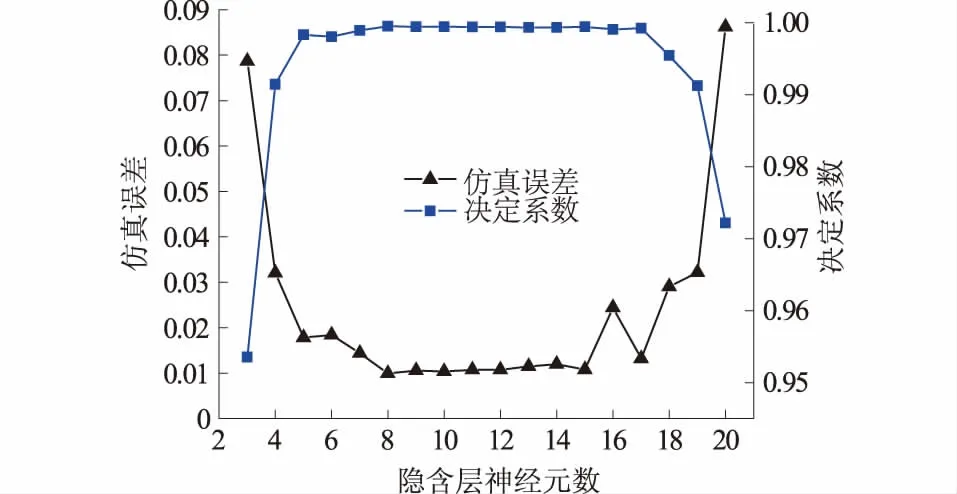
图3 隐含层神经元数与ELM性能的关系Fig.3 Relationship between the number of neurons in the hidden layer and the performance of ELM

由图3可知，对于不同的隐含层神经元数，ELM预测效果不同，总体来看效果均较好。决定系数均在95%以上，仿真误差最大不超过0.09。神经元数为8～15时，网络预测性能最好。综合比较后，将隐含层神经元数选为8，即网络结构为“2-8-1”。此时用检验样本进行检验，结果见图4。

由图4可见，此训练的ELM预测精度较高，预测值与实际值几乎完全重合，仿真误差为0.005 7。ELM拟合出的安全系数K与随机变量c和φ之间的关系，即响应面函数K=f(c,φ)如图5所示。

3.4 蒙特卡罗模拟求解边坡可靠度

图5 ELM拟合出的功能函数曲面Fig.5 Functional surface fitted by ELM

为了选择合适的模拟次数，利用MatLab软件的normrnd函数分别生成不同数量(由模拟次数确定)的随机样本数据，依次求解边坡的安全系数，进而得到失效概率。由于每次生成的样本不同，失效概率也会有差别。重复20次蒙特卡罗模拟，得到这20个失效概率的变异系数与模拟次数的关系如图6所示。

图6 模拟次数与失效概率的变异系数之间的关系Fig.6 Relationship between the number of simulation and the coefficient of variation of failure probability

图7 安全系数的频数分布直方图Fig.7 Frequency distribution histogram of safety factor

由图6知，边坡失效概率的变异系数随模拟次数增加而减小，即模拟次数越多，精度越高。当模拟次数较少(<50 000)时，失效概率的变异性较大，准确性差；当>50 000次时，失效概率的变异系数较小，在10%左右，且基本趋于稳定，为了使结果更加准确，兼顾精度与效率，本文采用100 000组随机参数样本进行边坡可靠度分析。

将生成的100 000组随机参数样本，代入前文已训练好的ELM中，得到100 000组安全系数值K，并绘制出K的频数分布直方图，见图7。

如图7所示，经统计，安全系数<1的个数为91个，根据“大数定理”可得该边坡失效概率Pf=91/100 000=9.1×10-4，由式(16)得边坡可靠度指标β为3.118。

文献[17]中，基于ANSYS和二次多项式拟合响应面函数所求的可靠度β=3.42，验算点法β=3.215，常规响应面法β=3.214，直接蒙特卡罗法β=3.234。结果均与本文较为接近，证明了本文方法的可行性，且与直接蒙特卡罗法求得的可靠度指标3.234相比，文献[17]所用方法误差为5.75%，本文方法为3.59%，精度相对较高。强度折减法程序内置于FLAC3D中，无需假定滑面形状，能够有效搜索最危险滑面，而原文利用ANSYS需在图形用户界面反复折减强度参数进行求解，耗时相对较多，且二次多项式拟合精度明显低于极限学习机。特别是当随机变量增加时，上述其他方法计算量较大，而采用极限学习机结合均匀试验可大幅提高可靠度分析的效率。

4 c和φ相关性对边坡可靠度的影响

为了与文献[17]所用方法进行对比，本文也将c和φ当作相互独立的随机变量。但大量统计数据表明，同一场地土的c和φ具有负相关性，且相关系数多在-0.5左右[20]。

将其他参数保持不变，研究c和φ相关性对边坡可靠度指标β的影响，如图8所示。

图8 可靠度指标和失效概率与c和φ之间相关系数的关系Fig.8 Relationship of reliability index and failure probability against coefficient of correlation between c and φ

由图8可知，c和φ间相关性对边坡失效概率和可靠度指标有较大影响，随着c和φ间相关系数的增大，边坡失效概率增大，可靠度指标减小。忽略c和φ间的负相关性会导致计算的失效概率偏大，可靠度指标偏小，不过这也可看作是一种安全储备。

5 结 论

本文提出了一种基于FLAC3D和极限学习机的边坡可靠度分析方法，并以具体边坡作为实例，利用均匀设计和FLAC3D强度折减法构造样本数据，通过极限学习机拟合响应面功能函数，结合蒙特卡罗模拟，得到了边坡失效概率和可靠度指标，并讨论了c和φ相关性对边坡可靠度的影响，忽略c和φ的负相关性会高估其失效概率。本文方法与其他方法结果相近，验证了该方法的可行性。该方法具有以下优点：

(1)利用均匀试验设计，只需较少的样本点便可确保其代表向量空间中的所有部分，大幅减少了试验次数，缩短了仿真计算时间。

(2)利用极限学习机构造边坡极限状态的响应面，拟合精度好、计算效率高，特别是对于具有高度非线性隐式功能函数的边坡可靠度分析，优势更明显。

(3)将极限学习机与传统的可靠度分析方法结合，既提高了计算效率，又避免了传统方法存在的一些缺点，为边坡可靠度理论与工程实践提供了一条新途径，具有广泛的应用前景。