基于解析法的Ti/Al3Ti层状复合材料断裂力学分析
原梅妮,李 瑶,魏成富,栾道成
(1.中北大学机电工程学院, 山西 太原 030051; 2.西华大学材料科学与工程学院, 四川 成都 610039)
近年来发展的以Al3Ti为基体、高强度钛合金为增强体的Ti/Al3Ti层状复合材料,除了具有高强度、高模量、低密度的优异性能外,还具有强大的抗冲击能力。许多国家已经考虑将这种复合材料应用于航空航天、舰船、现代化武器装备等高技术领域[1-2]。目前国内外学者利用实验和数值模拟的方法对Ti/Al3Ti层状复合材料的断裂行为与力学性能进行了广泛研究。Price等[3]利用四点弯曲实验研究了韧性金属的体积分数对Ti /Al3Ti层状复合材料力学性能的影响,分析了在垂直与水平方向加载时复合材料的性能差异。Zhou等[4]利用实验分析了Ti/Al3Ti层状复合材料在准静态和高应变速率情况下的界面性能和断裂机制,研究了应变率对界面性能的影响。王泽明等[5]利用ENF和MMF测试方法分析了Ti/Al3Ti层状复合材料的层间裂纹断裂行为,通过实验对Ⅱ型及Ⅰ+Ⅱ型裂纹的能量释放率进行了比较。马李[6]建立了三点弯曲试样的有限元模型以模拟Ti/Al3Ti叠层材料的裂纹扩展形式,分析了复合材料层数、组元体积分数对裂纹扩展的影响。
本文基于梁的纯弯曲理论以及裂纹扩展的能量原理,利用四点弯曲试样的力学模型对Ti/Al3Ti层状复合材料的断裂行为进行了理论分析,通过裂纹偏折与扩展条件推导出裂纹能量释放率间的关系式,并分析了材料层数、层厚比对材料性能的影响。
1 Ti /Al3Ti 层状复合材料的断裂力学分析
1.1 力学模型及应力分析
图1为Ti/Al3Ti层状复合材料四点弯曲试样的力学模型。试样由金属间化合物Al3Ti层与韧性金属Ti层组成,Al3Ti层数m=2n-1(n为正整数),总层数为2m-1。Ti层的厚度、弹性模量分别为h1、E1;Al3Ti层的厚度、弹性模量分别为h2、E2;满足关系h=h1+h2。假设梁为有限长梁,跨度为2L,总厚度为H,宽度为B,并做出材料力学假设:1)H/(2L)≤0.2,细长梁;2)w(x)/ρ(x)≤1,小挠度梁。

图1 Ti/Al3Ti层状复合材料四点弯曲力学模型
材料力学中,梁纯弯曲部分受到的弯矩相等,且只有横向应力,该部分应力表示为
(1)
在图1所示的坐标系下对应力进行面积积分,得到弯矩表达式为
(2)
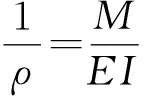
(3)
用等效抗弯刚度Σ表示EI,得到Σ的表达式为

(4)
化简可得
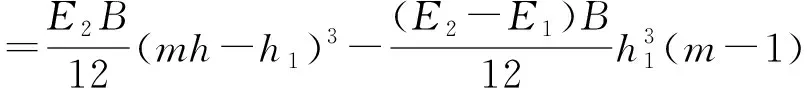
(5)
矩形梁的最大弯曲正应力发生在离中性轴最大位移处,即H/2处,所以最大弯曲正应力表达式为

(6)
1.2 断裂分析模型
由于韧性金属Ti层的作用,Ti /Al3Ti层状复合材料发生断裂时形成Ⅰ型和Ⅱ型裂纹,扩展形式为垂直扩展和界面扩展。在裂纹的传递过程中,其扩展驱动力可用能量释放率G来表示,当能量释放率高于临界值时,裂纹发生扩展。
图2所示为Ti/Al3Ti层状复合材料四点弯曲试样裂纹扩展模型。在该模型仍符合梁的纯弯曲假设的基础上对其做出进一步假设。

图2 Ti/Al3Ti层状复合材料四点弯曲试样裂纹扩展模型
1)断裂过程。实验的加载方式为位移加载。当加载点C位移达到临界值时,梁上缘跨中由于受到的横向应力最大,最先达到梁的强度极限而发生断裂,出现垂直方向(图2模型中的y方向)裂纹。垂直裂纹扩展至临界长度后,停止继续沿垂直方向扩展,在界面处改变方向,开始沿界面在水平方向扩展(假设同时向两边对称扩展),水平裂纹扩展长度达到临界长度后停止扩展。此过程中加载点位移保持不变,所有裂纹扩展所需能量完全由试样的应变能提供。随着外部载荷的继续加载,裂纹发生进一步扩展,最终使Ti /Al3Ti复合材料试样完全失效。
2)界面扩展。一次加载后,梁上只有最深一层界面裂纹发生扩展,之前已经扩展的界面裂纹长度保持不变,该部分脱离梁整体失去抗弯能力,不再参与裂纹扩展。
3) 应变能释放率。考虑到弱界面层影响,垂直裂纹扩展临界应变能释放率按混合率估算,即Γv=Γ1h1/h+Γ2h2/h。四点弯曲试样在相位角ψ=40~60°时,界面裂纹扩展临界应变能释放率近似认为不随裂纹长度变化而变化[7-9]。
1.3 垂直裂纹扩展能量释放率Gv

在Ti /Al3Ti层状复合材料中,钛合金Ti-6Al-4V的弹性模量E1为116 GPa,Al3Ti的弹性模量E2为216 GPa[10]。韧性金属增韧机制为:通过层板间的相互作用产生桥接韧带,为裂纹尖端的闭合提供牵引力,以及通过发生塑性变形来提升复合材料的抗裂性能。考虑到Ti层对垂直裂纹扩展的影响,参考垂直裂纹扩展临界应变能释放率Γv的估算方法,在求解垂直裂纹能量释放率Gv时同样按照混合率计算,Gv的计算公式为
(7)
纯弯曲试样的应力强度因子[11]的计算公式为

(8)
式中:t为垂直裂纹的扩展长度;M为四点弯曲试样纯弯曲部分的弯矩。
每次断裂过程并不是独立存在,而是和相邻的断裂过程存在一定关系。Hn、Hn-1分别为第n次、第n-1次裂纹扩展前的材料的厚度,tn、tn-1分别为第n次、第n-1次垂直裂纹扩展长度,mn为第n次裂纹扩展后Al3Ti层的剩余层数。根据定义,Hn和mn的表达式为:
Hn=Hn-1-tn-1;
(9)
mn=(Hn-tn)/h。
(10)
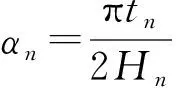

(11)
把M=pl、式(8)代入式(7),得到垂直裂纹扩展能量释放率的计算公式为

(12)
1.4 界面裂纹扩展能量释放率Gi
在线弹性情况下,加载点位移y与外载荷P成正比,即
y=CaP。
(13)
构件的柔度C是裂纹长度a的函数,能量释放率的计算公式为
(14)
文献[7]利用积分法推导出梁的纯弯曲部分与非纯弯曲部分的挠曲线方程,由式(13)、(14)可得到Gi的表达式,结果表明Gi与最深一层界面裂纹临界长度an到达的区域有关。具体表示为:
1)an>L(即an到达AB区)

(15)
2)an≤L(即an到达OA区)
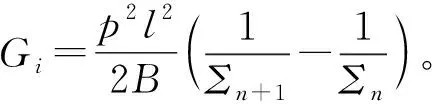
(16)
1.5 裂纹偏折与扩展
由垂直裂纹和界面裂纹扩展能量释放率,可进一步分析垂直裂纹的拐折现象。随着裂纹扩展,垂直裂纹能量释放率Gv逐渐减小,垂直裂纹扩展到界面时不具备穿透界面条件,转向沿界面扩展,此时满足条件[12]
(17)
如图2所示,假设界面裂纹临界长度an扩展到OA区,将式(12)、(16)代入(17)可得:

(18)
由式(11)、(18)以及假设3)的公式,可求解αn,进一步可得垂直裂纹扩展长度tn与Al3Ti层剩余层数mn。
垂直裂纹拐向界面后,由复合材料应变能所提供的能量仍会使裂纹沿界面扩展。将p=-yn/Cn代入式(16),可得到Gi的表达式
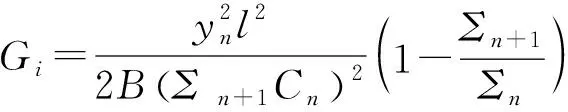
(19)
式中:柔度Cn与an有关;yn为垂直裂纹起裂时的加载点位移。
随着界面裂纹扩展,Gi不断减小。当满足条件
Gi≤Γi,
(20)
裂纹扩展停止。由式(19)、(20)可求出界面裂纹临界长度an。
对于所求的an,如果an≤L,则an正确;若an>L,则须用式(15)重新求解an。
随着外部载荷继续增加,当Gi>Γi时,界面裂纹继续扩展,当梁上应力满足σxmax≥σb(σb为Al3Ti极限强度),垂直裂纹再次起裂,新裂纹扩展随之开始。
1.6 裂纹起裂
随着外载荷的增大,Ti /Al3Ti层状复合材料试样上缘跨中的应力逐渐增大,当σxmax≥σb时,垂直裂纹开始扩展。此时σxmax表达式为
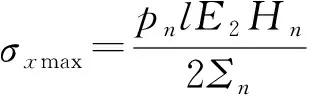
(21)
所以裂纹起裂的临界载荷为
(22)
加载点L+l处的位移为
yn=pn·Cn,l+L。
(23)
多次加载直到Ti /Al3Ti层状复合材料试样完全断裂。利用计算的pn、yn绘制成载荷-位移曲线。曲线与坐标轴之间的面积值表示整个断裂过程所消耗的断裂功。
2 算例分析
2.1 四点弯曲试样算例
用制备好的Ti /Al3Ti层状复合材料四点弯曲试样进行验算,可得如下数据:E1=116 GPa,h1=0.23 mm,E2=216 MPa,h2=0.94 mm,m=9,H=10.6 mm,B=4 mm,L=50 mm,l=10 mm,σb=220 MPa,Γ1=164 J/m2,Γ2=19 J/m2,Γi=17 J/m2。
按照复合材料断裂过程编写程序,设置终止条件,代入上述数据可得图3所示的Ti /Al3Ti层状复合材料四点弯曲试样的载荷-位移曲线。

图3 Ti /Al3Ti层状复合材料四点弯曲试样载荷-位移曲线
Vecchio等[13]利用三点弯曲和四点弯曲实验对同一个陶瓷纤维增强Ti/Al3Ti层板复合材料试样断裂韧性进行了研究,得到不同的载荷-COD曲线,根据ASTM E399标准[14]利用曲线得到的起裂断裂韧性相等,证明四点弯曲实验可以研究非脆性材料的断裂行为,得到的载荷-COD曲线可以反映复合材料断裂过程。
算例计算出临界起裂载荷为1 451 N,利用式(24)得到算例中Ti /Al3Ti层状复合材料四点弯曲试样临界断裂韧性。
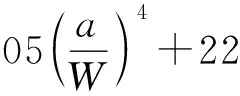
(24)
Ti体积分数为14%~20%时,通过实验得到Ti/Al3Ti起裂断裂韧性为15~23 MPa·m1/2[15]。算例中Ti /Al3Ti层状复合材料四点弯曲试样Ti的体积分数为17.8%,起裂断裂韧性KO为15.443 MPa·m1/2,计算与实验得到的起裂断裂韧性数值接近,说明本文分析方法可以研究Ti /Al3Ti 层状复合材料断裂过程,算例的载荷-位移曲线可以反映Ti /Al3Ti层状复合材料四点弯曲试样断裂过程。
对于偏差,分析如下。
1)Ti /Al3Ti 层状复合材料制备方法是交替叠放Al板与Ti板,通过热压工艺烧结合成,该过程中Al板与Ti板发生化学反应生成Al3Ti[1]。这种制备工艺导致材料存在残余应力、孔洞、表面氧化等缺陷,材料性能不能达到预期设计要求。
2)与裂纹实际扩展过程相比,裂纹偏折与界面扩展的耗能机制约占所有耗能机制的71%[7]。桥接、脱粘和分层裂纹等现象[16]产生的应变能为裂纹的扩展提供了能量。
2.2 材料几何参数对断裂功的影响
层状复合材料设计目的是在保强增韧前提下,使裂纹扩展转向界面,尽可能沿界面扩展较远距离,消耗更多能量。为研究材料的增韧机制,改变材料几何参数计算pn、yn得到断裂功,与相同尺寸的Al3Ti块体试样做对比,分析Ti /Al3Ti层状复合材料断裂功与Al3Ti断裂功比值变化。
材料增韧机制分为内部增韧和外部增韧[17-19]。内部增韧是材料微观结构抵抗裂纹扩展的固有属性,任何能引起位错运动或塑性区域规模的行为都属于内部增韧机制。外部增韧是通过层板间的物理联系达到增韧效果,常见的外部增韧包括裂纹偏折、裂纹尖端钝化、裂纹桥接、应力重新分配等。材料整体增韧效果由内部增韧与外部增韧共同决定。
1)层数对材料性能影响。
Al3Ti的层数小于9时,由于材料厚度影响,内外增韧机制未有效发挥作用。随着层数增加,内部增韧和外部增韧对材料的影响逐渐增大,图4中曲线迅速上升,同时材料在加工过程中形成的微观裂纹和孔洞等缺陷增多,受到外载荷作用时,这些缺陷成为应力集中点,在Al3Ti层中会加快微观裂纹扩展,在Ti层中会使晶体发生位错,产生塑性变形。宏观裂纹首先在Al3Ti层产生[26],随着裂纹扩展,裂纹尖端附近应力迅速增大,附近Al3Ti层的微观裂纹生长导致脆性断裂,而Ti层发生屈服生成小型塑性区,使裂纹发生尖端钝化延缓裂纹扩展。当裂纹扩展到界面时,在Ti层进一步扩展有2种方式:1)沿Ti层切应力最大方向发生偏折,引导裂纹离开最大应力面,降低局部应力强度;2)将应力传递到远离裂纹一侧,使裂纹重新成核,消耗大量能量,增加材料韧性。无论以哪种方式裂纹都会继续扩展,裂纹尖端之后的区域发生应力重新分布,未断裂的Ti层在经历强化、颈缩阶段后最终发生断裂。另一方面,层数增多后,界面裂纹增多。界面通过桥接限制基体裂纹扩展,但同时受到高剪切应力作用而发生剥离,导致层板间脱层,造成灾难性破坏[23]。综上所述,随着层数增加,外部增韧机制对增韧效果的影响逐渐增大,在层数为9时,内部增韧与外部增韧的综合作用使材料性能达到最佳。再增加层数,界面破坏增多,结构整体的性能有所下降,但内部增韧仍然为主要断裂机制,在图4上表现为曲线缓慢下降。

图4 不同层数对断裂功的影响
2)层厚比对材料性能影响。
层厚比(Al3Ti/Ti)可以用组元体积分数来表示。由于Al3Ti发生脆性断裂,裂纹最先在Al3Ti中产生,然后再扩展到金属层。由于Al3Ti的极限强度比Ti高,与裂纹偏折、桥接等现象相比,Al3Ti层的微观缺陷发展成宏观裂纹需要消耗更多能量,Al3Ti体积分数增加使结构消耗更多能量,这一变化在图5上表现为层厚比0—5时曲线上升,且斜率较大。金属层在内部增韧中起决定性作用,在外部增韧中也扮演着重要角色。金属Ti体积分数减少,内部增韧这一固有属性的增韧效果直线下降,材料发生塑性变形消耗能量减少,外在增韧的裂纹尖端钝化、桥接等现象对裂纹扩展的抵抗力有所下降,再减少Ti体积分数,材料会出现明显的脆性断裂。但是金属Ti的厚度保持不变,增大Al3Ti体积分数意味着材料厚度也增加,复合材料裂纹扩展路径变长。对复合材料整体来说,层板韧性下降所减少的断裂功由裂纹扩展路径变长所增加的断裂功来补偿,再增大层厚比对材料整体断裂功影响不大。如图5所示层厚比为5之后的曲线几乎不再发生变化。

图5 不同层厚比对断裂功的影响
3 结论
本文利用梁的纯弯曲理论和裂纹扩展的能量原理对Ti /Al3Ti层状复合材料四点弯曲试样进行了断裂力学分析,得到如下结论。
1)基于四点弯曲模型建立的解析方法能较好反映Ti /Al3Ti层状复合材料的主要断裂行为。
2)通过编程,可以观测Ti /Al3Ti层状复合材料的裂纹扩展和外部加载,得到载荷-位移曲线,计算出断裂功。
3)由材料几何参数对断裂功的影响曲线可知,Ti /Al3Ti层状复合材料中Al3Ti层层数为9、层厚比为5时抗冲击性能达到最优。
本文以Ti /Al3Ti层状复合材料为基础进行分析,分析结果对于具有相同结构、相似组元的其他金属间化合物基层状复合材料也具有参考价值。
校友作者介绍

原梅妮(1974—),女,山西运城人,西华大学材料加工工程专业2002级硕士研究生。2008年在西北工业大学获得博士学位。山西省项目评审专家、教育部学位论文评审专家、中国航空宇航协会会员。
主持完成国家自然科学基金、教育部博士点基金、大飞机关键构件重大专项子项目、中央军委装备部等国家、省部级科研项目20余项。以第一作者发表论文100余篇,SCI收录15余篇,EI收录20余篇。申请发明专利8项,授权发明专利5项。担任Materials and Design、稀有金属材料与工程等多种国内外期刊审稿人。

