正激变换器的非线性行为

刘俊良，江传奇

（北方民族大学，宁夏 银川 750000）

0 引 言

DC-DC变换器在很多领域都有着极其广泛的应用，如家用电器、工业自动化、通信、军工等。由于变换器中开关器件动作的频繁性，在其运行中会发生很多预想不到的情况，如间歇性震荡、较大的噪音、电磁间的相互干扰、系统的突然紊乱等。开关电源是一种高频化电能转换装置，是当代电子信息产业迅猛发展中不可或缺的一种电源形式。DC-DC变换器属于开关电源的核心部分，性能的好坏对于开关电源的性能影响巨大。当某些电路参数发生微小变化时，DC-DC变换器会呈现出丰富的非线性动力学行为，如分岔、混沌现象等。而这些现象的产生会使电路系统在运行过程中发生剧烈的振荡，使系统失稳，严重时甚至导致系统崩溃[1]。随着现代电力电子技术的飞速发展，各行各业对开关电源性能的要求日益提高。因此，对DC-DC变换器的非线性分析以及用混沌控制策略对其进行控制显得至关重要。

理论上，目前DC-DC变换器中非线性问题的分析和研究，己经成为开关电源领域的一个重要课题。根据非线性动力学理论在DC-DC变换器领域研究的现状，研究较深入的工作还是一些非隔离型的DC-DC变换器，即电能直接传递，不经过变压器。但是，这些非隔离型的DC-DC变换器并不能满足工业需求。因此，需要加入具有转换功能的变压器构成隔离型变换器来克服这一缺点，如正激变换器、半桥变换器、全桥变换器和推挽变换器等。所以，本文以B变压器隔离型Buck（即Forward Converter）为研究对象，从离散迭代模型的建立、非线性动力学行为分析以及混沌控制策略等方面，进行数学分析和仿真分析[2]。

实践上，在DC-DC变换器的工程应用中，工程师和科学家由于没有从本质上对变换器的非线性特性进行深层次了解和研究，往往只是盲目地根据自己长期以来的工作实践经验设计开关电源系统，导致在电路参数设计时或多或少会有一些随机和盲目，易造成电路系统在实际运行中由于某些电路参数在一些敏感系数微变时发生震荡，甚至直接烧坏器件。这种情况需要工作人员耗费不必要的人力和物力去调整实验参数，直到整个电路系统趋于稳定，大大降低了工程项目的进度。因此，系统分析和研究DC-DC变换器的非线性动力学行为，对开关电源系统的电路参数设计具有重要的指导意义。根据上述分析，本文对隔离型正激变换器进行了更深层次的探索，以更加了解变换器的分岔和混沌行为，为系统的参数设计提供理论数据[2]。

1 正激变换器离散模型的建立

正激变换器采用电压反馈式方式对电路构成一个回路，电路的整体结构如图1所示。设定变换器电路在CCM的模态下工作。当全控型开关S导通时，负载电压增加。当负载电压和参考电压Vref相等时，开关管S关断。由基尔霍夫定律得出系统的状态方程，此电路涉及变压器，需对其模型进行简化，整体结构如图2所示。

在实际运用中，正激变换器的功率变压器不是理想化的，其中掺杂着很多影响因素，如寄生电容、寄生电感等。如果在建立离散迭代数学模型时考虑这些因素，将会给推导和仿真带来很大困难[3]。为了更便捷地分析电路，要参考一些有关磁性器件的简化，尤其是有关变压器的书籍。由现阶段掌握的知识和内容，只能运用变压器的一些主要参数，如初级绕组Lm、漏感Le，由此可以求出简化后初级和次级线圈的电压。变压器简化模型如图2所示。

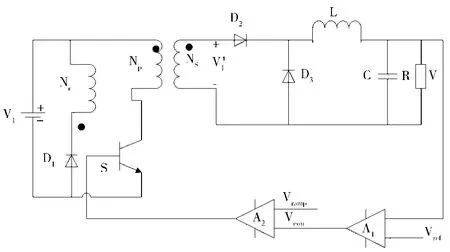
图1 电压反馈型Buck变换器的主电路

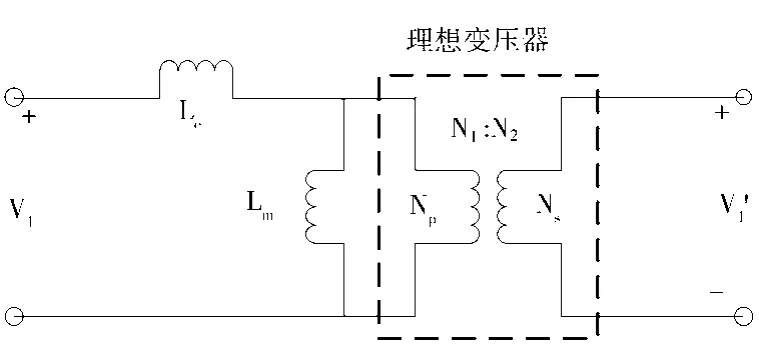
图2 功率变压器简化模型

变压器初、次级电压关系为：

系统的状态方程为：

经过求解上述微分方程，并且离散化得出系统的离散迭代模型为：

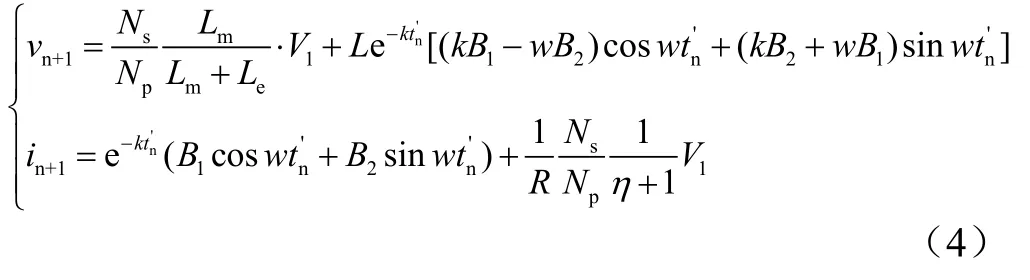
2 正激变换器中分岔和混沌现象的仿真分析

对于非线性动力学特性的研究，可以借助庞加莱截面、相图、频谱、时域波形图、分岔图等方法来判断分岔和混沌状态的运行情况。其中，分岔图是分析系统分岔和混沌行为最清晰、最有效的工具。基于正激变换器的离散迭代模型，可以利用MATLAB的m函数作分岔图进行数值分析。对于分岔图，描述系统的运行状态是由一系列的离散点构成，将这些离散点用线依次连接形成线条。当系统进入非线性行为历程时，通过计算得到大量不单一离散点，将这些点连接起来就构成了非线性现象。因此，对于分岔图，当一个敏感系数有所改变时，系统由周期状态到非线性状态的过程就呈现在分岔图中。

从理论方面分析，对于DC-DC变换器，任何一个敏感电路系数发生微小改变时，都会引起整个系统的非线性状态。在这一部分，主要以正激变换器的负载电阻R、放大系数A为分岔参数分析非线性动力学特性。

运用MATLAB的m函数对正激变换器的离散数学模型进行迭代计算，以负载电阻R为分岔参数，取值范围是20～100 Ω，迭代的步长为0.1 Ω，得出的图形就是分岔图，如图3所示。

由图3可知，当负载电阻在20～48 Ω时，系统处于稳定状态。当负载电阻为48 Ω时，正激变换器出现倍周期分岔，电路系统进入2周期状态；当负载电阻继续增大时，系统最终进入混沌状态。

以放大系数a为分岔参数，利用MATLAB扫描3＜a＜6.5的范围，得出正激变换器的分岔图，如图4所示。

从图4可以看出，当3＜a＜6.5时，正激变换器从稳定的1周期状态到混沌状态。当a=6.5时，电路系统处于稳定的1周期状态；当a=5.8时，电路系统处于稳定的倍周期状态；当a=3时，电路系统处于稳定的混沌状态。

3 正激变换器稳定性分析

DC-DC变换器是强非线性动力学系统，因此在对其进行电路参数进行设计时，需要求出它们稳定工作的参数区间。因此，分析系统稳定性十分必要。本节采用求根轨迹的方法分析系统的稳定性，首先在Buck变换器离散映射数学模型的基础上，求出系统的雅克比矩阵。当选定一个分岔参数（如输入电压）扫过一定范围时，可以用Matlab中的m函数进行仿真，得出其周期轨道特征值运动轨迹，然后分析其稳定性。其次，引入功率变压器得出初级、次级间电压的关系，得出正激变换器的特征值根轨迹图，分析其稳定性。

对于正激变换器的稳定性分析，本文采用状态空间平均法求解变换器的离散映射数学模型，由此选取电容电压和电感电流为状态向量。

分析之前，为了更方便的研究，作出如下两个假设：

（1）正激变换器工作于电感电流连续模式，只存在两个工作模态；

（2）正激变换器中各个元器件是理想的。

由此，得出系统的状态方程为：

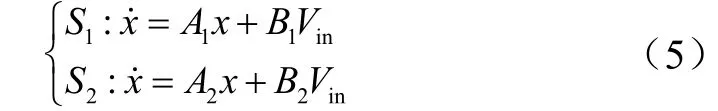
可以得出，正激变换器的1周期和2周期状态的特征值根轨迹图。输入电压Vin为分岔参数，在10～30 V扫描，得到特征值的根轨迹图，如图5、图6所示。

由图5、图6所示，系统的特征值开始在一个半径小于1的内圆上运动，且是一对共轭复数。直到它们运动到实轴上，特征值变成实数。当Vin=18.5 V时，特征值穿过单位圆。当Vin＞18.5 V时，特征值穿过了单位圆，系统从稳定的1周期状态变成不稳定的状态。可以看出，当Vin=19 V时，特征值已经运动到单位圆外，系统此时处于不稳定状态。当特征值穿过单位圆，系统将进入2周期状态。

由图6所示，加大输入电压，2周期系统的特征值在半径小于1的内圆上运行，直到它们运动到实轴，特征值变成实数。当Vin=28.7 V时，特征值将穿过单位圆。当Vin＞28.7 V时，特征值穿过单位圆，系统将从2周期状态在此发生分岔，系统进入4周期状态。当Vin=29 V时，系统处于4周期状态。

本节运用状态空间平均法，得出正激变换器的离散数学模型，在此基础上求出系统的雅克比矩阵，运用MATLAB的m函数得出系统的特征值运动轨迹，并对此轨迹进行分析，得出系统稳定性的变化轨迹。通过正激变换器稳定性分析，得出了正激变换器的稳定工作区间。

4 结 论

本文分析了隔离型变换器——正激变换器的非线性动力学特性。首先，求出功率变压器简化后的离散数学模型。在分析离散数学模型的基础上，分别以负载电阻R和放大系数a为分岔参数，用MATLAB的m函数做出变换器的分岔图；分析了随着负载电阻和放大系数的变化，系统从周期到分岔直到混沌的变化过程，验证了正激变换器非线性行为的正确性；运用状态空间平均法，得出正激变换器的离散数学模型，在此基础上求出系统的雅克比矩阵，运用MATLAB的m函数得出系统的特征值运动轨迹，并对此轨迹进行分析，得出系统稳定性的变化轨迹；通过正激变换器稳定性分析，得出了正激变换器的稳定工作区间。

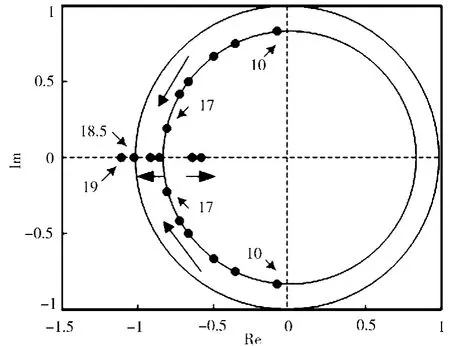
图5 1周期轨道特征值根轨迹图

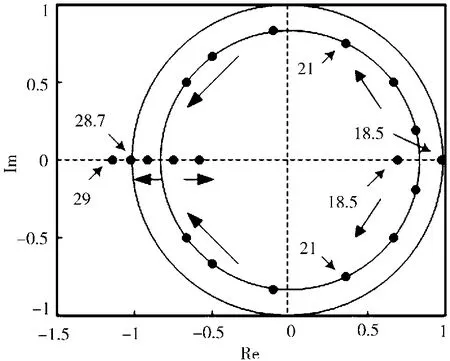
图6 2周期轨道特征值根轨迹图