基于MFOA算法的电力系统无功优化和补偿控制研究

王 政，苑向宇，薛满宇

（北京京能清洁能源电力股份有限公司，北京 100028）

0 引 言

电力能源对经济发展尤为重要。工业发展、生活需要等都离不开电能。因此，为了更好地促进经济的发展，国家应当制定完善的电力系统发展规划，为经济的发展提供安全、可靠、稳定又环保的电力能源[1]。可借助调节设备的帮助如无功补偿，使得电力系统的有功损耗最小。如今，非线性内点法和群智能算法两种算法是无功优化和控制的最常用方法，二者各有优缺点。非线性内点法[2]对离散数据或者变量而言，可操作性不大，但是对较为集中的变量数据，具有较好的收敛性和稳定性。群智能算法可以用来处理较为离散的变量，且可以在全局进行寻优，如遗传算法[3]（GA）、粒子群算法[4]（PSO）等。然而，这种算法有一个突出的缺点就是容易陷入局部寻优，且处理变量和寻优的速度很慢。

群智能算法中还包括一种所控制的参数较少且收敛速度相对较慢但结果准确度高的算法。这种算法通过模拟果蝇觅食行为进行计算，简称为FOA，是英文Fruit Fly Optimization Algorithm的缩写，中文名为果蝇优化算法[5]。通过查阅文献，未发现将此理论应用于电力系统无功优化和控制的研究。由于这种算法容易陷于局部最优，因此作者采用修正补充后的果蝇优化算法研究电力系统无功优化和控制，即MFOA，英文名称为Modif i ed Fruit Fly Optimization Algorithm。最终的计算结果发现，优化修正后的算法结果更准确，速度较快，表现较好。

1 果蝇优化算法

优化修正后的果蝇算法具体步骤如下。

第1步：将算法中的相关参数进行初始化，果蝇群体大小设为popsize，用Iteration代表果蝇的最大迭代数，begin代表开始，用X_begin和Y_begin分别表示果蝇的初始位置。

第2步：设xi和yi为位置，计算单只果蝇的寻优方向和寻优距离Value。

式中，xi和yi都代表果蝇个体的位置，Value代表果蝇的搜索距离。

第3步：根据计算式（3）和式（4）计算单只果蝇寻优地点距离出发点的距离di，其中si代表单只果蝇的味道浓度。

第4步：利用以下函数式（5）计算单只果蝇目前所处位置的味道浓度。

第5步：在一群果蝇所找到的味道浓度中寻找最优，用Smellb表示，xb和yb分别表示寻到的最佳位置。

第6步：用Smellbest=Smellb表示果蝇的最佳位置和做好的味道浓度，将试验结果记录并保存下来，设果蝇的初始位置分别为然后寻找最佳方向。

第7步：进行迭代计算，即循环试验计算第2～5步，如果味道浓度并不比前一迭代味道浓度优质，那么将返回执行第2～5步；反之，不再重复，执行第6步。

2 修正型果蝇优化算法

观察式（3）和式（4）可以发现，当式（4）求倒后，果蝇的味道浓度判定函数si会变得很小，这时就不是全局寻优，而成为局部寻优，会出现“早熟”问题[6-7]。

如果将β设为修正因子，对FOA进行修正优化，可得到优化后的FOA，即MFOA，那么就会避免陷入局部寻优问题。

优化后的果蝇优化算法：

其中，sMi表示MFOA算法的味道判定函数。

其中，g服从均匀分布，K表示常数。

3 无功优化数学模型

3.1 目标函数

在给定负荷和无功补偿装置地点的基础上，以电力系统有功网损最小为目标函数，其数学模型如下[8]。

其中，PL表示有功网损；表示对各节点电压越限的惩罚函数项；表示对发电机无功功率越限的惩罚函数项[9]。

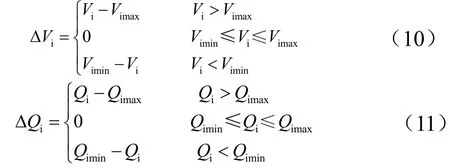
3.2 约束条件

等式约束条件：

不等式约束条件：

4 实证分析

图1为EEE30节点系统拓扑结构。这样可以对此论文中所采用的算法进行检验，看其是否有效，是否足够可靠。图1中，第1节点、第2节点、第5节点、第8节点、第11节点以及第13节点分别有6台发电机。在这6台发电机中，有4台发电机可以调节变压器，分别位于支路上，依次为4-12、6-9、6-10、27-28。此次试验中，同时设有无功补偿设备，第6、19、27以及30节点处装有这种设备。

图1 IEEE30节点系统拓扑

4.1 不同算法优化结果对比

果蝇群体大小为20，最大迭代次数为100，优化结果如表1所示。

表1 MFOA、FOA、PSO和内点法优化结果对比

观察表1可以发现，修正后的果蝇优化算法比上文提到的FOA、PSO以及内点法三种算法收敛速度更快，计算过程所使用的时间更少。

4.2 不同算法收敛速度对比

将不同算法随机任意运行多次（4次以上），记录研究果蝇优化算法、修正后的果蝇优化算法以及其他两种算法（PSO和内点法）的收敛速度，最后对所记录得到的数据进行对比分析。结果表明，修正后的果蝇优化算法的收敛速度较其他算法更快，具体参见图2。

4.3 潮流计算结果

分析表2和表3可以发现，相较于计算结果为0.093 8原来的果蝇优化算法，使用修正后的果蝇优化算法的有功损耗是0.100 9，说明修正优化后的算法可以将网损降到很小。另外，这种算法可以改善电压水平，因此整体优化效果良好。

5 结 论

通过查阅相关文献发现，尽管果蝇优化算法可以通过控制较少的参数较快收敛而使结果较准确，但是还未被用来研究电力系统无功优化和控制。因此，为了避免这种算法的弊端，将其进行修正优化并应用于电力系统。MFOA算法在研究IEEE30节点系统时，较未修正的果蝇优化算法、内点法以及PSO算法，在计算结果准确度和收敛速度快慢方面更具优势，算法效果较好。

表2 MFOA和FOA算法的潮流计算电压计算结果

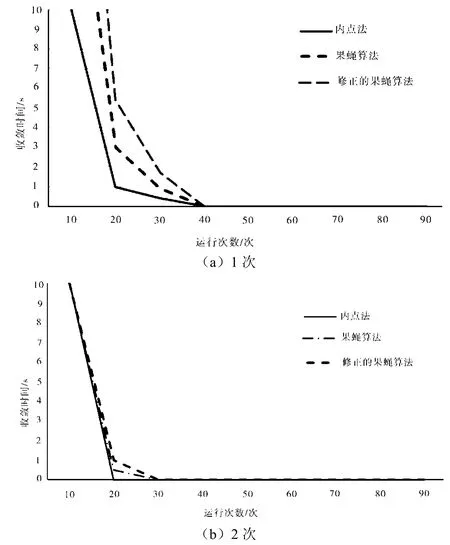
图2 收敛速度对比图

表3 MFOA和FOA算法的潮流计算结果