基于泰勒展开法的结构混合可靠性分析

孟广伟， 魏彤辉， 周立明， 李锋

(吉林大学 机械与航空航天工程学院, 吉林 长春 130025)

0 引言

工程结构设计中广泛存在着材料特性参数、载荷和几何尺寸等有关的各种不确定性[1],概率模型是处理上述不确定信息的有效途径之一。但概率模型对测试数据的强依赖性和实际工程中可得数据的缺乏，在一定程度上会引起可靠性计算结果产生较大误差[2]。近年来发展起来的非概率区间分析方法，只需获取不确定参数的界限或范围，得到工程人员的关注。Ben-Haim等[3]认为由于概率可靠性在概率模型中对小误差非常敏感,在没有足够的信息来支撑概率模型时，宜采用区间集合模型来描述不确定性。Qiu 等[4]提出了不确定性、非随机参数的非概率区间模型，并采用子区间摄动技术对桁架结构进行结构优化。郭书祥等[5]通过将不确定参数进行区间描述，提出了一种非概率可靠性的度量体系及分析方法。王晓军等[6]通过将不确定性信息用区间集合来描述,提出了一种非概率集合的结构可靠性分析模型。邱志平等[7]以区间数学为理论基础,提出了结构灵敏度的区间分析方法。乔心州等[8]通过理论及实例对区间分析法和凸模型方法的求解结果进行比较，得出区间分析法更接近Monte Carlo仿真(MCS)方法的解区间。云永琥等[9]用区间变量对梁结构的不确定变量进行描述，建立了梁结构共振非概率可靠性模型，并结合优化方法求解其可靠性指标。

结构的某些不确定性参数在实际工程中已累积大量的样本，但另外一些不确定性参数由于测试难、成本高等问题只能获得少量的样本。因此，采用单一的概率或者区间不确定模型难以进行有效分析。为了解决此类问题，目前已有学者研究了概率与区间混合不确定性模型及其可靠性分析问题。Du等[10]提出了一种可靠性优化方法，以解决概率变量和区间变量混合的不确定性问题。王军等[11]提出了一种新的概率- 非概率模型，通过一个典型结构和一个机翼下壁加筋板论证了混合模型的有效性。肖宁聪等[12]对认知不确定性用区间变量进行建模，随机不确定性用随机变量进行描述，建立了基于均值1阶鞍点近似的不确定性统一分析模型。文献[13-16]基于概率模型和非概率区间模型，提出了多种高效的混合可靠性分析方法。孙文彩等[17]根据随机- 区间变量耦合性质的不同，将问题划分为4类，并建立了相应的可靠度指标。刘帅杰等[18]采用区间与概率混合可靠性分析方法对星载网状天线的展开过程可靠性进行了分析和评估。尽管目前已有许多关于概率与区间混合模型的可靠性研究，但是，一方面这些方法大多需要对功能函数迭代以求得最可能失效点，而功能函数在迭代过程中可能存在不收敛的情况；另一方面在工程实际中，往往需要先已知基本变量的统计矩，再得到其概率分布。但由于信息的缺乏，获得的数据往往只能描述变量的统计参数，而它们的一些分布概型不能被准确地确定，若分布概型推断错误，则将对失效概率计算结果会产生较大误差。

本文结合区间泰勒展开法、降维算法、四阶矩法进行结构的混合可靠性分析。运用区间泰勒展开理论和降维算法，将功能函数展开为只含n个一维随机变量函数的和函数；利用泰勒展开方法并结合随机变量的前4阶中心矩，计算得到功能函数的前4阶中心矩；借助于四阶矩法，最终计算得到结构功能函数的失效概率区间。

1 区间泰勒展开

若结构中存在随机变量和区间变量，则结构功能函数表达式为

Z=g(x,yI)，

(1)

(2)

直接求解混合结构的失效概率是非常困难的，本文将区间问题转换为近似的确定性问题。为此，将g(x,yI)在区间变量yI的中点yc作泰勒展开，并忽略高阶项，可得

(3)

(4)

(5)

式中：gR(x,yI)和gL(x,yI)分别表示功能函数的上界和下界。

2 降维算法

结构功能函数g(x,yI)可表达为递增层级的低阶函数的和函数，其一般形式为

(6)

式中:g0为常数项；gi(xi,yI)为变量xi和yI共同作用时对结构功能函数的1阶表达；gij(xi,xj,yI)为变量xi、xj和yI共同作用时对结构功能函数的2阶表达；随后各项分别反映了逐渐增加的所有变量共同作用时对结构功能函数的影响。

随机样本降维(RS-HDMR)方法和中心切面降维(Cut-HMDR)[20-21]方法是两种常用的降维方法。本文在Cut-HMDR方法的基础上采用一种基于原始输入- 输出关系的替代模型。在Cut-HDMR方法中，通过g(x)输入空间中与中心点c=(c1,c2,…,cn)相关的信息来近似地表达g(x)，则展开的各分项表达式为

(7)

文献[22]指出，对于充分光滑的结构功能函数，高阶项对其影响要小于低阶项，因此，只保留低阶项可以近似表示功能函数。

在矩法计算和可靠性分析中，文献[23]指出中心点c的最优点值为各变量的均值μx.

综上可得n维函数g(x,yI)的单变量表达形式为

(8)

式中：g(xi,yI)=g(μx1,…,μxi-1,xi,μxi+1,…,μxn,yI)为一维函数；g(x0,yI)=g(μx1,…,μxi,…,μxn,yI)为常数项。

由(8)式可得功能函数的近似表达，主要是将高维函数g(x,yI)展开为由n个一维函数g(xi,yI)叠加的形式。

3 功能函数统计矩

在工程结构的可靠性分析中，点估计法是求解功能函数统计矩比较常用的方法。但点估计法只用到随机变量的前3阶矩，改进后也可用到第4阶矩，但计算精度都不如泰勒级数展开[24]，且点估计法也会受到均值、变异系数等诸多因素的影响导致计算结果精度下降。因而本文借助于泰勒展开理论，得到结构功能函数的前4阶中心矩。

(9)

(10)

(11)

(12)

4 结构失效概率计算

由第3节得到功能函数上界和下界的统计矩后，可基于矩估计法来计算失效概率区间。Zhao等[25]依据所研究问题的不同复杂程度，分别采用极限状态函数的2阶矩、3阶矩和4阶矩来计算失效概率。其中，二阶矩法和四阶矩法比较容易实现且四阶矩法的精度较高。因此，本文结合功能函数上界的前4阶矩，得到失效概率上界表达式为

(13)

(14)

(15)

(16)

(17)

(18)

5 数值算例

算例1考虑如下的极限状态方程：

(19)

式中:x1、x2和x3为随机变量，其分布类型和分布参数如表1所示。y1和y2为区间变量，其取值范围分别为[2.821 5,2.878 5]和[1.485,1.515].

为了验证本文方法的有效性，此算例中给定了随机变量的分布类型，以便与区间MCS方法[26]进行对比，图3是区间MCS方法计算流程图。

表1 基本变量的统计特征值

在结构可靠度计算中，区间MCS方法被认为是一种准确的计算方法。在操作系统为Windows 7、处理器为Intel Core i7、安装内存为8 GB的配置环境下运行，表2是算例1的失效概率计算结果。由表2可得，本文区间MCS方法的样本数为107，其中区间变量的划分数目为20，且在运行时间远低于区间MCS方法的基础上，本文失效概率上界和下界的相对误差仅为1.59%和0.95%，与区间MCS方法计算所得结果基本一致。

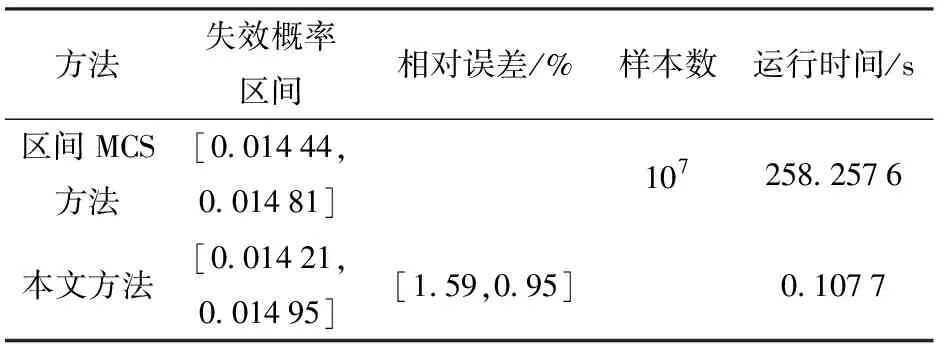
表2 算例1失效概率结果

算例2某型号货车车架为边梁式结构，由主纵梁、副纵梁各1根，横梁共6根所组成，各梁之间主要通过螺栓、铆钉和部分焊接连接而成。该车型的额定载重是2.5 t，长度是4.633 m，宽度是1.69 m，高度是0.17 m，使用的材料是Q235-A钢。车架相应的荷载参数如表3所示[27]。

表3 某型货车车架荷载参数

车架的垂直刚度对于车架的整体性能非常重要，因此需要进行可靠性分析。用垂向最大位移来代表垂直刚度，可以得到结构功能函数如下：

Z=dmax-d(x,yI)，

(20)

式中:dmax=0.92 mm和d分别表示垂向可允许最大位移和垂向实际位移。假设：驾驶室的重量为F1；储油箱的重量为F2；货物的重量为F3；弹性模量为E.F1、F2和F3为随机变量，其分布参数如表4所示。E为区间变量，其取值范围为[207.9 GPa,212.1 GPa]。其中，随机变量F1、F2和F3因样本容量不足，无法准确获知其分布类型，因此只给定其统计矩。为更真实地获得车架的受力情况，建立了货车车架的有限元模型，如图4所示。

表4 某型货车车架参数统计表

依据本文方法，首先利用降维算法，将结构功能函数进行单变量降维表达，再将所得降维表达式进行泰勒展开，利用(4)式和(5)式，获得结构功能函数上界和下界的表达式；由于降维后的功能函数上界和下界表达式仍然是隐性函数，因此，本文调用货车车架结构的有限元程序，得到其相应的最大位移；结合给定的随机变量前4阶中心矩，利用(9)式～(12)式，最终获得结构功能函数上界的统计矩，同理可得结构功能函数下界的统计矩；将所获矩信息作为系数代入(13)式～(18)式中，即可获得结构功能函数下界的失效概率，同理可得结构功能函数上界的失效概率区间。在较短运行时间的情况下，本文计算所得失效概率区间为[0.064 53, 0.089 24].

若将本算例中区间变量E的取值范围表示为[Ec-βEc,Ec+βEc]，其中中心值Ec=2.1×105，β为偏离中心值的偏差系数。图5中给出了β取0.005、0.010、0.015、0.020、0.025时概率分析方法和本文分析方法的失效概率变化趋势。从图5中可以看出，随着β的增大，本文分析方法的失效概率区间也越来越大。

若采用概率分析方法，将区间变量E设为随机变量，均值取Ec，标准差为βEc/3. 从图5中可以看出，概率分析方法的失效概率值介于本文分析方法失效概率上界和下界之间，表明本文方法的正确性。另外，本文分析方法失效概率上界大于概率分析方法的失效概率值，说明本文方法更安全，且更符合工程实际。

6 结论

本文提出了一种带区间变量的结构可靠性分析方法，并在工程实际中得到了应用。所得主要结论如下：

1)利用泰勒展开和降维算法建立结构功能函数的一维随机变量降维表达式，无需运用多重积分对功能函数的统计矩进行计算，无需迭代搜素最可能失效点。

2)结合四阶矩概率分析方法，给出求解随机- 区间混合模型最大失效概率的具体步骤，可对变量分布类型未知的混合模型进行可靠性分析。

3)数值算例表明本文方法不仅具有计算时间少、收敛速度快等优点，而且可处理功能函数为隐式或高维非线性的失效概率计算问题。