基于智能全站仪的隧道超欠挖面积计算方法

胡 博

(秦皇岛市测绘大队 河北秦皇岛 066001)

0 引言

在隧道工程中,快速、准确地计算隧道的超欠挖面积，对保障施工安全、控制工程成本、推进工程进度有着重要意义。智能全站仪的出现，为隧道断面检测提供了强大、便捷的方法。通过编写相应的应用程序，可以实现隧道断面的自动化检测和实时计算。目前，已有大量针对隧道断面检测的机载应用程序的研究，但现有的超欠挖面积计算的方法，多是将超挖面积和欠挖面积分解成多个三角形，再对各个三角形的面积求和，计算出单个超欠挖区域的面积[1，2]。此方法计算过程较为繁琐，需要判断不同的隧道断面情形，并且将弧形的隧道设计断面分解为若干个小三角形，是一种近似计算的方法,并非严密计算的方法。

基此，本文提出应用格林公式，以快速、精确计算隧道超欠挖面积。

1 格林公式

格林公式，描述了平面上沿闭曲线L对坐标的曲线积分与曲线L所围成封闭区域D上的二重积分之间的密切关系，提供了计算封闭区域面积的精确方法[3]，由其推导出的面积表达式为：

由于隧道断面线实质上为平面上的直线和曲线，因此，应用格林公式计算隧道超欠挖面积具有可行性。本文由此出发，研究适用于智能型全站仪编程的数学模型、数据结构以及程序算法。

2 数学模型

首先，建立断面坐标系，坐标系原点定义为轨面零高程线和断面中心轴的交点，以轨面零高程线为X轴，面向隧道前进方向水平向右为正方向，以断面中心轴为Y轴，竖直向上为正方向。

如图1所示，在断面坐标系下中，虚线为设计断面线，实线为实测断面点的连线，JD1、 JD2、JD3……为隧道断面实测点连线与设计断面的若干交点。JD1和JD2、JD2和JD3之间的实测线段和设计线段分别构成了封闭的面域A12和A23。面域A12的面积为JD1和JD2之间的超挖面积，面积A23的面积为JD2和JD3之间的欠挖面积。

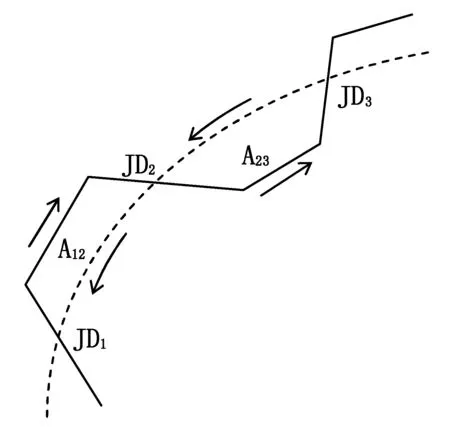
图1 实测与设计元素围成的超欠挖面域

基此，将包围超欠挖面域的封闭路径的前进方向定义为：“从起始交点出发，沿实测线段顺时针方向行进，到达下个交点后沿设计线段逆时针返回”。如图1所示，包围面域A12的封闭曲线的路径为：由JD1出发沿实测线段顺时针行进到JD2，再由JD2沿设计断面线逆时针行进回到JD1；包围面域A23的封闭曲线的路径为：由JD2沿实测线段顺时针行进到JD3，再由JD3沿设计断面线逆时针行进回到JD2(这里的顺、逆时针是相对于整个封闭的隧道断面而言)。

这样，包围超挖面域的封闭路径前进方向相对其包围的面域始终是顺时针，如A12。包围欠挖面域的封闭路径的前进方向相对于其所包围的面域始终是逆时针，如A23。按照这样定义的曲线积分的路径，应用格林公式计算出的超挖部分面积和欠挖部分面积正负号正好相反，于是通过积分结果的正负号来判定属于超挖还是欠挖，相同正负号的计算结果累加，就能得到总的超挖面积和欠挖面积。

当前的隧道工程中，常见的设计断面形状，主要有圆形、矩形、马蹄形。其中，矩形断面是由直线段相接构成的，马蹄形断面则由弧度、长短不同的多段圆弧相接构成，而圆形断面亦可看作圆心角为360°圆弧。因此，可以认为，隧道的设计断面由直线段和圆弧两种元素构成，设计断面与实测断面相交所形成的各超欠挖部分，也均由圆弧和线段两种元素来表达。

为了便于计算机编程实现，需要将线段和圆弧表示为参数式。

线段的参数表达式为：

x(t)=x1+tLcosA

y(t)=y1+tLsinA

其中，x1、y1分别为线段起始点坐标；

L为直线的长度；

A为直线的方位角；

t为从0到1变化的参数。

圆弧的参数表达式为：

x(t)=xc+Rcos(A1-At)

y(t)=yc+Rsin(A1-At)

其中，xc，yc为圆心坐标；

A1为圆弧起始方位角；

A为圆弧的圆心角；

R为圆弧半径；

t为从0变化到1的参数。

这样，将公式(1)转化为：

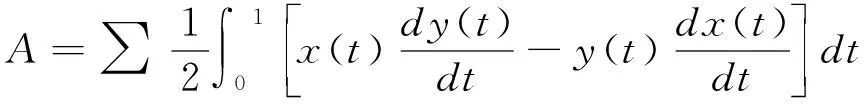
即针对组成封闭面域的各线段和圆弧进行0到1的分段积分，并将积分结果求和，得出该封闭面域的面积。

综上所述，利用格林公式积分可计算出超欠挖部分的面积，利用积分结果的正负号可以判断出所计算出的面积属于超挖还是欠挖。这样，对不同正负值的面积计算结果进行累加，便可得到总的超挖面积和欠挖面积。

3 数据结构

搭载Windows Mobile操作系统的智能全站仪提供了C#语言的开发工具，在此用C#语言设计隧道断面的元素类如下：

//圆弧类

Public class Arc

{

//圆心点坐标

Private point2d center_point;

//起始方位角

Private double begin_angle;

//圆弧圆心角

Private double angle;

//圆弧半径

Private double r;

//起点坐标

Private point2d begin_point;

//终点坐标

Private point2d end_point;

//构造函数

Public void Arc(point2d center_point,double begin_angle,double angle,double r)

}

//线段类

Public class Line

{

//起点坐标

private point2d begin_point;

//终点坐标

Privte point2d end_point;

//线段方位角

Private double a;

//线段长度

Private double length;

//构造函数

Public void Line(point2d begin_point,point2d end_point);

}

在Arc和Line类中，所有成员变量均设置为只读变量，仅由类的构造函数进行赋值。将设计断面以及实测断面表示为Arc和Line的链表，采用.net平台的ArrayList数据结构进行顺序存储。

求解两交点间封闭面域的面积，需要求得各交点的坐标，以及两个交点间的设计断面和实测断面的元素信息。因此，设计交点类如下：

public class JD

{

//交点的坐标

private point2d crd;

//交点所在的设计元素段链表中的索引

Private int id_survey;

//交点所在的实测元素段链表中的索引

Private int id_design;

//构造函数

Public void JD(point2d crd,int id_survey,int id_design)

}

4 程序算法

首先，读取隧道断面的全站仪实测坐标，生成实测元素链表list_survery，读取隧道断面的设计元素，生成设计元素链表list_design，并遍历链表所有元素，求出实测断面与设计断面的所有交点：

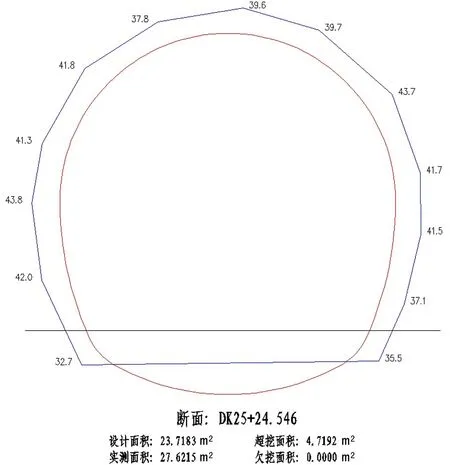
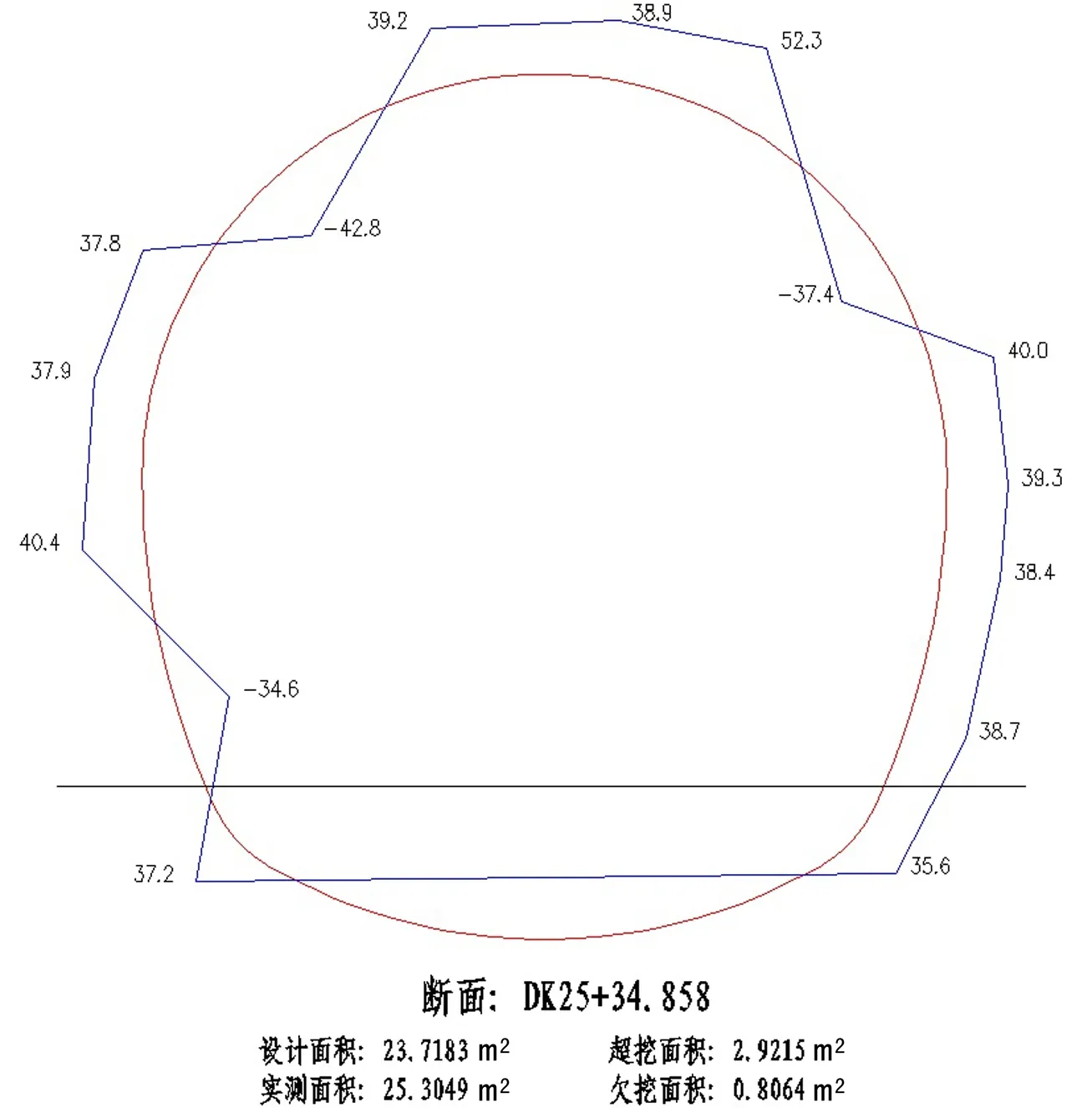
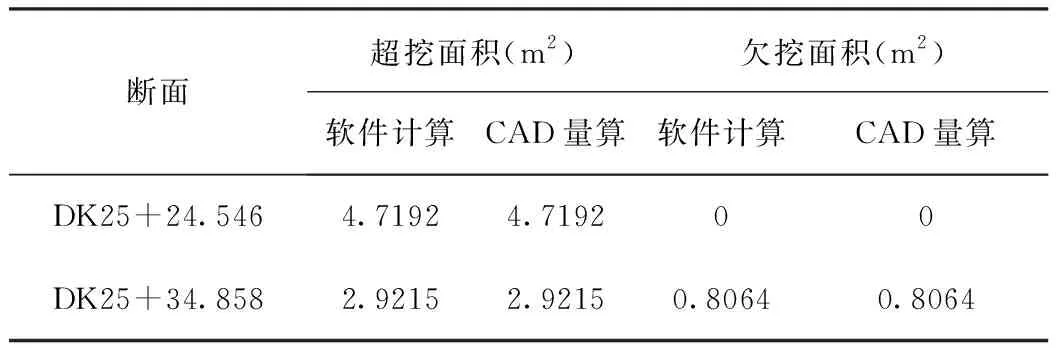
for(int i=0;i

for(int j=0;j

CalculateJD(list_survey[i],list_design[i]);

CalcualteJD为计算两线段、圆弧元素交点的函数。此处遍历设计断面和实测断面中所有的元素，两两组合求解其交点坐标，若交点存在，则创建JD类的实例，存储交点坐标和生成交点的元素在其list_survey和list_design链表中的索引i和j。所有的JD实例依次存储于链表list_JD中。

接下来，求解各个面域的超欠挖面积：

for(int i=0;i

{ CalculateArea(list_JD[i],list_JD[i+1]); }

CalcualteArea(list_JD[list_JD.Count-1],list_JD[0]);

CalculateArea为依据list_JD链表中相邻的两个交点，计算两交点间封闭面域面积的函数。此函数中，首先依据JD类中存储的实测断面元素和设计断面元素的索引，找出list_JD[i]和list_JD[i+1]之间以及list_JD[list_JD.Length-1]和list_JD[0]之间的所有设计与实测元素，并用交点对其所在的线段和圆弧元素进行截取，生成新的构成两交点间封闭面域的Arc和Line元素序列；然后，应用公式(2)对此序列进行分段积分，再求和算出两点间面域的面积。

最后，判断积分结果的正负号并分别累加，正的总和即为总超挖面积，负的总和即为总欠挖面积。

5 应用实例

应用武汉地铁二号线虎泉-名都区间DK25+24.546和DK25+34.858断面检测数据作为实验数据，输出AutoCAD文件格式的计算报告，并用AutoCAD图上面积量算数据作为比较基准，以验证本文算法的正确性和精度。

该断面为典型的多段圆弧组成的马蹄形断面。由于断面实测数据均为超挖，为了充分验证算法有效性，人为修改了DK25+34.858断面的实测数据，使其出现欠挖部分。计算报告，如图2～图3所示。

图2 DK25+24.546断面计算报告

图3 DK25+34.858断面(修改后)计算报告

本文算法计算结果与AutoCAD图上量算结果如表1所示。

表1 对比分析结果

对比表明，本文提到的算法计算结果与CAD图上量算结果完全吻合，具有很高的精度。

6 结语

应用格林公式能够方便精确地计算出不规则封闭区域的面积，本文从此思路出发，结合隧道断面的特点，给出了适合于计算机编程的数据结构和具体的计算过程，并应用地铁隧道断面检测数据进行了实验验证。

相较于现有的将超欠挖面域分解为若干个三角形，分别求解各个三角形面积再求和的近似计算方法，提出的方法具有以下优点：

(1)精度高。采用函数式表达设计和实测断面的各个元素，应用积分的方法计算超欠挖面积，数学模型严密，计算结果精确。

(2)通用性好。从单一思路出发，不必事先判断是超挖还是欠挖；应用统一的线段、圆弧模型来表达隧道断面，无需考虑各种各样复杂的隧道断面形式，都能够得出计算结果。

(3)易于编程。本文提出的元素类模型设计简单合理，算法清晰明了，利于计算机编程实现，能够极好地应用于智能全站仪的隧道断面检测软件开发。