广义双循环群上Cayley图中的处处非零3-流
李良辰,张小霞,张会芹
(1.洛阳师范学院 数学科学学院,河南 洛阳 471934;2.信阳师范学院 数学与统计学院,河南 信阳 464000)
0 前言
文中除特别说明外,图都是简单无向的有限图.未作说明的概念和符号参见文献[1].
设A是具有一个2阶元y的交换群.广义双循环群G=Dic(A,x)是由群A和元素x生成,且满足
[G:A]=2,x2=y,
并且对任意的a∈A有x-1ax=a-1.
设D(Γ)是图Γ的一个定向,记E(Γ)为图Γ的定向边的集合.如果E(G)中的边e=uv的方向是从顶点u指向v,则称u为e的起点,v为e的终点.对V(G)中的任意顶点v,定义
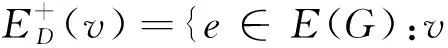
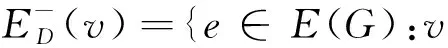
设整数k大于等于1.如果实值函数
f:E(Γ)→{0,±1,±2,±(k-1)},
对于任意的v∈V(Γ),有
则称函数f是图Γ上的一个k-流.定义
S(f)={e∈E(Γ):f(e)≠0}.
如果S(f)=E(Γ),则称k-流f为处处非零k-流.整理流理论是Tutte[2,3]研究四色问题时引入的,并提出了著名的3-流猜想.
猜想1 每个4-边连通图存在处处非零3-流.
Jaeger[4]证明了每个4-边连通图存在处处非零k-流.图中处处非零3-流是否存在引起了众多学者的研究兴趣.2012年,THOMASSEN[5]做出重要突破,证明了每个8-边连通图存在处处非零3-流.随后,Lovász等[6]改进这个结果,证明了每个6-边连通图存在处处非零3-流.尽管如此,猜想1仍然没有解决.
设G是单位元为1的有限群,S是G-{1}的子集并且S=S-1.我们构造一个图Γ=Cay(G,S),Γ的顶点集合V(Γ)=G,而边集合E(Γ)={gh:g,h∈G且g-1h∈S},称为群G关于S的Cayley图.
图Γ到自身的同构映射称为自同构.图Γ的全体自同构在置换乘法之下构成一个群,称为Γ的全自同构群,记为Aut(Γ).显然1≤Aut(Γ)≤Sym(Γ).如果Aut(Γ)在顶点集V(Γ)上传递,则称Γ为点传递图.容易证明,每个度为k的点传递图都是k-边连通的[7].因此,如果猜想1成立,那么度不小于4的点传递图存在处处非零3-流.
在所有的点传递图中,我们了解最深刻的莫过于Cayley图.POTOCNICK等[8]证明了交换群上的度不小于4的Cayley图存在处处非零3-流.对非交换群,ALSPACH等[9]证明了每个度不小于2的可解群上的Cayley图存在处处非零4-流.YANG等[10]验证3-流猜想对于定义在二面体群上的Cayley图是成立的.文献[11]推广了他们的结果.受此启发,我们主要研究定义在广义双循环群上的Cayley图中处处非零3-流的存在性.
1 预备知识及引理
一个连通的2-正则图称为圈.设n为大于等于2的正整数,含有n个顶点的圈记为Cn,含有n个顶点的路记为Pn.设有两个图Γ1和Γ2.图Γ1和Γ2的笛卡尔积Γ1□Γ2是以V(Γ1)×V(Γ2)为顶点集的图,其中Γ1□Γ2的两个顶点(u1,v1)和(u2,v2)相邻当且仅当u1=u2,v1v2∈E(Γ2)或u1u1∈E(Γ1),v1=v2.
设V(Pn)={1,2,…,n},V(K2)={1,2}.在图Pn□K2中添加边(1,1)(n,1)和(n,2)(1,1)的图称为循环梯,记作CLn.若在图Pn□K2中添加边(1,1)(n,2)和(1,1)(n,1),则所得之图为莫比乌斯梯,记作MLn.这两种图统称为闭梯,记作Ln.对于1≤i≤n,边(i,1)(i,2)称为闭梯Ln的横档.闭梯Ln所有横档构成的集合记作ER(Ln).
引理1[2]一个3-正则图存在处处非零3-流当且仅当它是二部图.
引理2 如果图Γ可以分解成边不交的子图并且这些子图是圈或3-正则二部图,那么图Γ存在处处非零3-流.
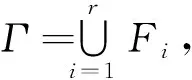
E(Fi)∩E(Fj)=ER(Fi)∩ER(Fj),i≠j.
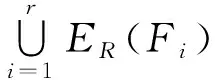
(4)不料孩子突然死亡,妇人又慷慨自杀,——我心将要怎样呢,而且她为什么死?老友,你知道么?她为爱我和你底妹妹而出此的。
引理4 设τ∈A是广义二面体群G的一个对合,a是G的一个阶大于等于3的元素,则Cay(G,{a,a-1,τ})是闭梯的并,并且其中的横档是由τ生成.
证明对于群G中任意的元素g,考虑下面两个圈
C:g,ga,ga2,…gas-1,gas=g,
C′:gτ,gτa,gτa2,…gτas-1,gτas=gτ,
其中s=orda.如果gτ∈V(C),则C=C′.不妨设gτ=gat,从而τ=at.又因为
τ2=(at)2=1,orda=s.
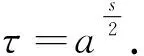
如果gτ∉V(C),则C和C′是不同的圈.如果a∈A,那么gai通过τ-边与gaiτ=gτai相邻,其中i=0,1,…,s-1.否则,设a=αtx,这里αi∈A,则有
gaτ=gαtxτ=gτa.
2 主要结论
定理1 若广义双循环群G=Dic(A,x)上定义的Cayley图Cay(G,S)的度不小于4,则Cay(G,S)存在处处非零3-流.
证明设Γ=Cay(G,S)是定义在广义双循环群G=Dic(A,x)上的度大于等于4的Cayley图.注意到,Γ是|S|-正则图.因为度为偶数的点传递图存在处处非零3流,故可设|S|是奇数.
群G中由两个对合生成的图或由一个阶不小于3的元素生成的图记为H.显然,H是图Γ的2-因子,所以图H存在处处非零3-流.从而,只需证明图G-H存在处处非零3-流.对|S|归纳可知,只需证|S|=5时定理成立即可.因为阶数大于2的元素是在S成对出现的,故S中含有奇数个对合.
由广义双循环群的定义可知,
Dic(A,x)={axi|i=0,1,a∈A}.
因为
(ax)2=ax·ax=aa-1xx=x2=y≠1,
所以广义双循环群的对合必包含于群A中.由于S的生成集,S中不可能含有5个对合.
若S包含3个对合,即
S={τ1,τ2,τ3,a,a-1},
其中τ1,τ2,τ3∈A;a,a-1∈G-A.容易验证由τ1,τ2,τ3-边生成的图同构于Q3.由引理4,
Γ1=Cay(G,{a,a-1,τ1})
是一个闭梯.显然,Γ=Q3∪Γ1,并且
ER(Q3)=ER(Γ1).
由引理3知,此时图Γ中存在处处非零3-流.
若S={τ,b,b-1a,a-1},其中τ∈A.根据引理4可得,Cayley图Cay(G,{a,a-1,τ})和Cay(G,{a,a-1,τ})都是以τ-边为其横档的闭梯的并.由引理3知,此时图Γ中存在处处非零3-流.证毕.
3 结束语
本文验证了定义在广义双循环群上的Cayley图中处处非零3-流的存在性,即Tutte的3-流猜想对这类图是成立的.这个结果为研究图中处处非零3-流的存在性提供了帮助.

