树的Zagreb指标的上界
李树立
(泉州师范学院数学与计算机科学学院,福建 泉州 362000)
1 预备知识
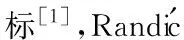
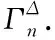
2 主要结果
定义1对于一个连通图G,第一类Zagreb指标M1(G)定义为
容易证明第一类Zagreb 指标也可表示为
引理1记图G的度序列为(d1,d2,…,di,…,dj,…,dn),其中d1≥d2≥…≥dn,若图G′的度序列为(d1,d2,…,di+1,…,dj-1,…,dn),则
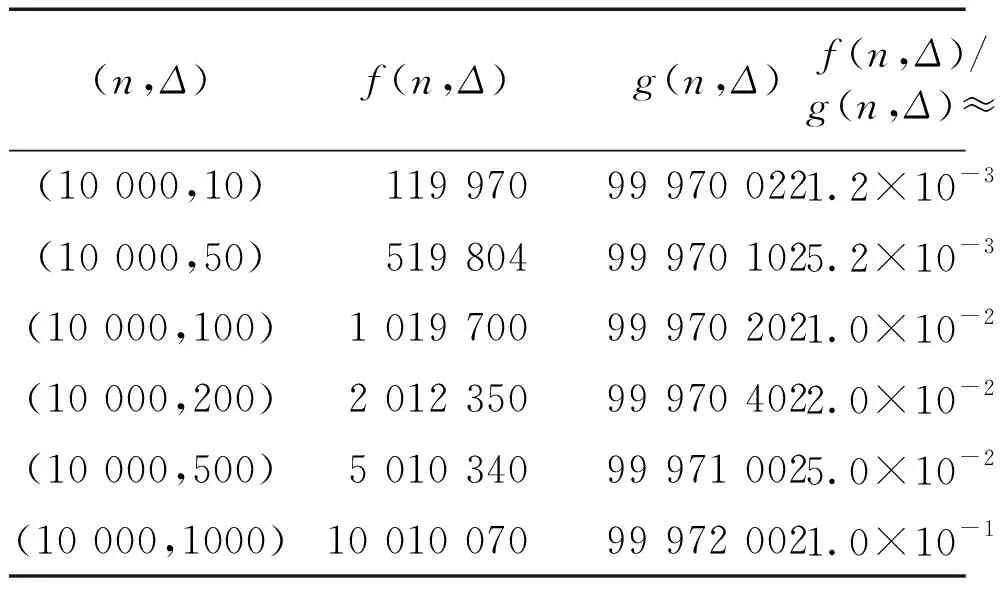
M1(G) 证明由定义1可知, M1(G′)-M1(G)=(di+1)2+(dj-1)2- di2-dj2=2(di-dj)+2. 因为di≥dj,故di-dj≥0,则M1(G′)-M1(G)>0,引理得证. 由于n个顶点的树有n-1条边,由握手定理可知 kΔ+s+n-k-1=2(n-1), 即 k(Δ-1)+s=n-1. 因为 1≤s<Δ, 所以 设Sn为n个顶点的星图,若有k个星图Sp1,Sp2,…,Spk,则连接Spi与Spi+1的中心点,i=1,2,…,k-1,所得到的图记为Sp1,p2+1,…,pk-1+1,pk.如图1所示. 图1 5个顶点的星图S5(a)及由4个星图S5,S4,S3,S5构造的星图S5,5,4,5(b)Fig.1 The star S5 of five vertices (a) and the new graph S5,5,4,5 constructed by S5,S4,S3,S5 (b) 由以上分析及引理1,可得到以下定理是显然的. 对于第一类Zagreb指标,Das等[10]得到了如下结果. 定理2[10]设T是顶点数为n,最大度为Δ的树,则 M1(T)≤n2-3n+2(Δ+1) 等式成立当且仅当T≅Sn,或T≅P4. 记 g(n,Δ)=n2-3n+2(Δ+1). 下面证明我们得到的上界优于Das等[10]得到的上界. 定理3对顶点个数为n及最大度为Δ的任意树,有f(n,Δ)≤g(n,Δ). n-1=(n-2)·(Δ+1)-ε(Δ2-1)+ [1+ε(Δ-1)]2+n-1=(n-2)·(Δ+1)+ n-(ε-ε2)(Δ-1)2. 因为0≤ε<1,2≤Δ≤n-1,则 f(n,Δ)≤(n-2)·(Δ+1)+n=(n-4)· (Δ+1)+n+2(Δ+1)≤(n-4)· n+n+2(Δ+1)=n2-3n+2(Δ+1)= g(n,Δ). 定理得证. 由定理3可知,定理1中的树的第一类Zagreb指标的上界优于Das等[10]给出的上界,一些数值比较见表1.由表1数据可以看出f(n,Δ)≤g(n,Δ). 表1 f(n,Δ)与g(n,Δ)的一些数值比较 Tab.1 Some numerical comparisons of f(n,Δ) and g(n,Δ) (n,Δ)f(n,Δ)g(n,Δ)f(n,Δ)/g(n,Δ)≈ (10 000,10) 119 97099 970 0221.2×10-3 (10 000,50)519 80499 970 1025.2×10-3 (10 000,100)1 019 70099 970 2021.0×10-2 (10 000,200)2 012 35099 970 4022.0×10-2 (10 000,500)5 010 34099 971 0025.0×10-2 (10 000,1000)10 010 07099 972 0021.0×10-1
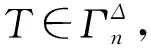


——泉州宋船

