高轨目标监视系统星座设计和探测效能分析

张科科，朱振才，周美江，胡海鹰，陈宏宇

(1.中国科学院上海微系统与信息技术研究所，上海 200050；2.上海微小卫星工程中心，上海 201203；3.中国科学院大学，北京 100049)

0 引 言

高轨空间尤其是地球同步轨道，分布着诸多重要战略型高价值卫星，如通信、数据中继、导航、导弹预警和军事侦察等，是人类进入空间、控制空间的战略高地，对高轨空间目标进行监视、跟踪和编目维护具有十分重要的意义。

空间目标监视有地基和天基两种手段，受地球曲率和气象条件限制，地基系统无法对全部空间目标进行全天时和全天候观测。天基系统相比地基系统，不受气象条件限制、探测范围广、观测精度高[1]，与地基系统可相互补充，受到各航天大国重视。

美国正在构建功能强大的天基目标监视体系，从轨道部署和工作模式可分为两类。

一种部署于低轨太阳同步轨道[2]，采用区域凝视模式[3]对高轨空间目标开展观测，24小时即可完成对整个同步带目标的扫描。其典型代表为天基空间监视(Space-based space surveillance，SBSS)系统，分两个阶段部署，第一阶段Block-10“探路者”卫星已于2010年9月25日发射[4]，进入630 km太阳同步轨道，并于2013年4月交付使用；第二阶段Block-20计划3颗卫星组成星座，预计2021年发射。SBSS系统建成后，将使美国对地球静止轨道卫星的跟踪能力提高50%，对空间目标编目信息的更新周期由现在的5天左右缩短到2天[5]。由于“探路者”卫星预计于2018年寿命到期，为避免在轨太空监视出现能力缝隙，美国空军于2017年8月26日发射一颗“作战及时响应空间”-5(ORS-5)卫星[6]，部署于低轨赤道圆轨道，为美国空间目标监视提供过渡能力。

另一种部署于地球同步轨道附近[7-8]，高于或低于标称地球同步轨道一定距离，通过自然漂移的方式对同步带目标开展近距成像观测，增加详细特征识别能力。其典型代表为地球同步轨道空间态势感知项目(Geosynchronous space situational awareness program，GSSAP)系统，第一期两颗卫星于2014年7月28日发射[9]，第二期两颗卫星于2016年8月19日发射[10]，4星组网，最快30天可完成对整个同步带目标的巡视侦察。GSSAP系统将支撑美军高轨态势感知能力向支持空间作战的目标技术侦察、行动意图判断等多个领域拓展。

天基空间目标监视系统的观测效能主要与天基平台的轨道部署、机动能力、探测载荷能力以及观测模式相关。在探测载荷能力和天基平台机动能力一定的前提下，轨道部署和观测模式具有内在联系，二者互为影响，共同决定了监视系统的观测效能。当前国内外学者对部署在低轨太阳同步轨道的天基平台的观测模式以及覆盖能力分析已有一定的研究[11-14]，但鲜见系统阐述高轨天基平台轨道部署与工作模式设计的文献。受GSSAP系统启发，设计一种运行于同步轨道附近、兼具对同步带目标远距离探测编目和近距离成像侦察功能的同步带目标高轨天基监视星座，并通过理论分析和仿真对星座部署及其效能问题进行研究。

1 同步带目标轨道分布

空间目标的轨道分布直接影响天基平台的轨道部署和工作模式设计。以参考文献[15]的数据分析同步带目标的轨道分布情况。对半长轴介于astad±500 km(其中astad=42166.261 km[16]，为J2模型下标称地球同步轨道半长轴)范围内390颗处于可控状态的目标进行分析，经统计有如下结论：

1)88.5%同步带目标半长轴介于astad±50 km内。

2)94.6%同步带目标偏心率小于0.001，所有同步带目标偏心率均小于0.1。

3)61.5%同步带目标倾角小于0.2°，85.1%同步带目标倾角小于5°。

4)除去-140°～-160°经度目标分布较少，其余经度均有同步带目标较为均匀地分布。

2 天基平台星座部署

2.1 轨道类型

根据第1节分析，同步带目标大多分布在标称地球同步轨道±50 km范围内，高轨天基平台选择亚同步带赤道圆轨道，轨道高度略低于标称半长轴h，偏心率为0，倾角为0°或180°，不仅可以对地球另一侧的同步带目标进行远距离扫描探测，与同步带目标的半长轴差还可以形成自然相对漂移，实现对地球同侧头顶上方同步带目标的近距离成像观测，原理如图1所示。考虑光学成像对太阳光照角的要求，将探测相机安装在平台对地面，远距离探测任务在太阳位于平台天顶一侧时开展；将成像相机安装在平台对天面，近距离成像任务在太阳位于平台天底一侧时开展。保证远距离探测和近距离成像开展任务的时间区间不同，保证天基平台在整个太阳变化区间都处于有效工作状态。

高轨天基平台采用亚同步带赤道圆轨道，轨道参数只有轨道高度、即与标称半长轴的差h未知。h由近距离成像任务决定，本文选择h=100 km。

2.2 星座设计

对高轨远距离探测任务，受平台姿态机动能力限制和地球遮挡，单星存在观测盲区，需要多星部署才能实现对全部同步带目标的遍历。多星部署的星座规模和星座配置方式由平台的姿态机动能力(机动范围、机动速度)和探测任务需求(观测弧长、遍历时间)决定。一般来讲，姿态机动范围越大，星座规模越小；姿态机动速度越快，遍历时间越短，相应观测弧长也越短。分别对两种轨道：0°倾角顺行轨道和180°倾角逆行轨道、采用两种姿态扫描方式：自西向东扫描和自东向西扫描下的星座规模和星座配置方式进行理论分析。

2.2.1参数约定

取地球常数μ=398600.4418 km3/s2，地球赤道平均半径Re=6378.137 km，计算如下参数。

1)平台相对目标的轨道角速度

标称同步带目标相对地心的轨道角速度为

(1)

高轨天基平台相对地心的轨道角速度为

(2)

采用顺行轨道和逆行轨道，平台相对同步带目标的轨道角速度分别为

ωSX=ωSat-ωTar=0.0009 (°)/min≈0

(3)

ωNX=ωSat+ωTar=0.5023 (°)/min≈2ωTar

(4)

2)平台的姿态机动速度

平台基础姿态指向采用对地定向，探测相机安装在平台对地轴，平台进行俯仰姿态机动带动探测相机对同步带目标进行扫描成像。设平台的俯仰姿态机动范围为±β，平台的俯仰姿态机动速度为ωAtt，则平台对同步带目标的扫描周期为

TAtt=2β/ωAtt

(5)

定义平台进行同步带目标扫描的速度比为

k=ωAtt/ωTar

(6)

3)等效地球遮挡角

平台进行姿态扫描时，由于地球遮挡，会形成探测盲区，对应地心角一半称为等效地球遮挡角，如图1所示。实际应用中，探测相机针对暗弱目标成像设计，对地球大气杂光抑制能力有限，在计算探测盲区时，需在地球遮挡的基础上加上相机的杂光抑制角，等效地气光对相机的影响。本文假设相机的杂光抑制角为γ=9°，则等效地球遮挡角为

θ=arcsin[Re/(astad-h)]+γ=17.7209°

(7)

4)扫描方向定义

从北极俯视，天基平台扫描方向与地球自转方向一致(即逆时针方向扫描)，定义为自西向东扫描；天基平台扫描方向与地球自转方向相反(即顺时针方向扫描)，定义为自东向西扫描。

2.2.2观测覆盖性

定义由平台姿态机动能力限制而导致的盲区为盲区1，由地球遮挡导致的盲区为盲区2，分别对平台采用顺行轨道和逆行轨道对应的盲区进行分析。

1)顺行轨道

当平台采用0°倾角顺行轨道时，近似认为其相对同步带目标静止，两种扫描方式下的盲区与可视区分布相同，如图2所示。

顺行轨道平台的盲区1和盲区2分别为

Φ1=2×2(90° -β)=360°-4β

(8)

Φ2=2×2θ=4θ

(9)

盲区1和盲区2相对平台和地心的连线对称分布，已知盲区1和盲区2，则可视区1和可视区2为

Ψ1=Ψ2=180°-Φ1/2-Φ2/2=2(β-θ)

(10)

2)逆行轨道

当平台采用180°倾角逆行轨道时，近似等效为地球和同步带目标不动，平台以两倍标称地球同步轨道角速度相对地球和同步带目标转动。

(1)盲区1

图3所示为平台采用自西向东方式进行扫描。平台从图①位置开始扫描，运行到图②位置时结束一次扫描。与顺行轨道不同，逆行轨道下的盲区1增加了平台在一个姿态机动周期内相对同步带目标(即地球)运行转过的部分，为

Φ1= 2(90° -β)+ωNXTAtt+2(90°-β)=

360° -4β(1-1/k)

(11)

图4为平台采用自东向西方式进行扫描。平台从图①位置开始扫描，运行到图②位置时结束一次扫描。与自西向东扫描盲区1的计算方式不同，自东向西扫描的盲区1由姿态能力限制导致的盲区与平台轨道转过的区域相减，为

Φ1= 2×2(90° -β)-ωNXTAtt=

360° -4β(1+1/k)

(12)

自东向西扫描方式下，当平台的姿态机动速度较慢时会出现如图5所示盲区1为零的情况。此时

(13)

即逆行轨道下，平台采用自东向西方式扫描，可以通过调整平台的姿态机动能力(机动范围β,机动速度ωAtt)使盲区1为零。从式(13)可以看出，机动速度ωAtt是机动范围β的单调增函数，即若平台的机动范围增加，机动速度也应随之提高，才能达到一定的匹配使盲区1为零。

(2)盲区2

图6为平台采用自西向东方式进行扫描。平台运行到图A位置时开始切入地球临边，运行到图B位置切出地球临边。与顺行轨道不同，逆行轨道下的盲区2不仅与地球遮挡角有关，还与姿态从切入地球临边到切出地球临边期间，平台相对同步带目标(即地球)运行转过的部分有关。

从位置A到位置B，平台姿态在对地定向的基础上转过2θ，耗时为

t*=2θ/ωAtt

(14)

可知在逆行轨道下，平台自西向东扫描时的盲区2为

Φ2=4θ-ωNXt*=4θ(1-1/k)

(15)

自西向东扫描方式下，由式(15)知当平台姿态机动速度减慢时，同样会出现盲区2为零的情况。此时

Φ2=4θ(1-1/k)≤0⟹ωAtt≤ωTar

(16)

即逆行轨道下，平台采用自西向东方式扫描，当平台的姿态机动速度ωAtt不超过标称地球同步轨道角速度时，盲区2为零。但慢的扫描速度意味着长的遍历时间，需要折中考虑。

图7为平台采用自东向西方式进行扫描。平台运行到图A位置时开始切入地球临边，运行到图B位置切出地球临边。与自西向东扫描时盲区2的计算方式不同，自东向西扫描的盲区2由地球遮挡角和平台轨道转过的区域相加，可得

Φ2=4θ+ωNXt*=4θ(1+1/k)

(17)

(3)两盲区分布

图8为自西向东扫描时的可视区1。从盲区1开始时平台所在位置①到盲区2开始时平台所在位置A，姿态在对地定向的基础上转过β-θ，用时为

t1A=(β-θ)/ωAtt

(18)

可知可视区1的表达式为

Ψ1= 180°-2θ-ωNXt1A-2(90°-β)=

2(β-θ)(1-1/k)

(19)

则可视区2的表达式为

Ψ2= 360°-Φ1-Ψ1-Φ2=

2(β-θ)(1-1/k)=Ψ1

(20)

图9为自东向西扫描时的可视区1。从盲区1结束时平台所在位置①到盲区2开始时平台所在位置A，姿态在对地定向的基础上转过β-θ，用时为

t2A=(β-θ)/ωAtt

(21)

可知可视区1,可视区2的表达式分别为

Ψ1= 180°-2θ-[2(90°-β)-ωNXt2A]=

2(β-θ)(1+1/k)

(22)

Ψ2= 360°-Φ1-Ψ1-Φ2=

2(β-θ)(1+1/k)=Ψ1

(23)

至此，得到两种运行轨道、两种扫描方式下的盲区与可视区分布如表1所示。

表1 两种运行轨道、两种扫描方式下盲区与可视区统计Table 1 Blind areas and visible areas of two orbits and two scanning modes

2.2.3观测弧长

设探测相机全视场角为φ。对顺行轨道，由于其相对同步带目标静止，观测弧长为

LSX=φ/ωAtt

(24)

对逆行轨道，观测弧长计算原理如图10所示。

推导出自西向东扫描时的观测弧长为：

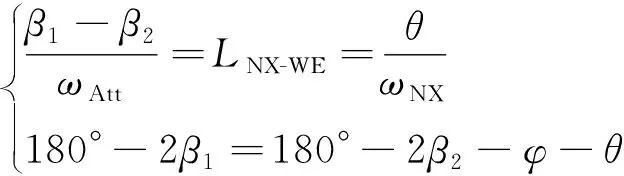
(25)

自东向西扫描时的观测弧长为：

(26)

2.2.4星座配置

由第2.2.2节可知，平台采用顺行轨道的总盲区为

ΦSX=Φ1+Φ2=360°-4(β-θ)

(27)

平台采用逆行轨道自西向东扫描的总盲区为

ΦNX-WE=Φ1+Φ2=360°-

4(β-θ)(1-1/k)

(28)

平台采用逆行轨道自东向西扫描的总盲区为

ΦNX-EW=Φ1+Φ2=360°-

4(β-θ)(1+1/k)

(29)

由式(27)、(28)、(29)可得如下结论：

1)三方案总盲区：ΦNX-WE>ΦSX>ΦNX-EW。即若采用单星观测，观测效率：逆行轨道(自东向西)>顺行轨道>逆行轨道(自西向东)。

2)顺行轨道下，可以通过增大姿态机动范围β减小总盲区；逆行轨道下，可以通过增大姿态机动范围β和增大(自西向东)或减小(自东向西)姿态机动速度ωAtt减小总盲区。

3)由于0<β-θ<90°，顺行轨道和逆行轨道自西向东姿态扫描的总盲区一定大于零；逆行轨道自东向西姿态扫描当满足如下关系时，总盲区为零。

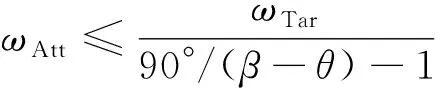
(30)

对单个平台总盲区大于零的情况，可采用双星星座配置，通过合理配置双星相位差Δu消除观测盲区。此时双星相位差与盲区和可视区满足如下关系

(31)

由于Δumin≤Δumax，式(31)转化为如下关系

max(Φ1,Φ2)≤min(Ψ1,Ψ2)

(32)

可求得，对顺行轨道，姿态机动范围β和姿态机动速度ωAtt(即k)应满足如下条件

(33)

对逆行轨道自西向东扫描，应满足

(34)

对逆行轨道自东向西扫描，应满足

(35)

2.2.5遍历时间

对单星就可以无缝遍历的情况，遍历时间为

TSin=TAtt

(36)

对双星配置才能无缝遍历的情况，遍历时间为

TDou=TAtt+Δu/TTar

(37)

2.2.6轨道优选

对采用顺行轨道、逆行轨道自西向东姿态扫描和逆行轨道自东向西姿态扫描三种方式,根据上文推导的公式进行可行解计算。设探测相机全视场角φ=3°；变量为姿态机动范围β和姿态机动速度ωAtt；计算可行解的筛选条件为天基平台数目N和观测弧长L，如表2所示。

计算得到三种方式的可行解分布如图11所示。从图11可以看出：

1)可行解：顺行轨道(900组) > 逆行轨道自东向西(367组) > 逆行轨道自西向东(84组)。

2)顺行轨道可行解在姿态机动范围和姿态机动速度取值区间上分布较为均匀；逆行轨道自西向东的可行解分布在姿态机动范围取值较大、姿态机动速度取值相对较小的窄区间上；逆行轨道自东向西的可行解分布在姿态机动速度较小的区间上。

表2 可行解计算条件设置Table 2 Feasible solutions computational conditions setting

三种方式所需天基平台数目、观测弧长、最短遍历时间对比如图12～图14所示，可得到三个结论：

1)在姿态机动范围较大(集中在67°～90°)、姿态机动速度较小(集中在0.3～1°/min)时，逆行轨道自东向西扫描方式单星就可以无缝遍历同步带目标，但遍历时间较长：8.87～18.62 h。

2)针对双星才能实现无缝遍历的情况，顺行轨道相比逆行轨道，观测弧长更长、遍历时间更短，具有优势。如图15为顺行轨道观测弧长减逆行轨道两种扫描方式观测弧长的结果，均大于零；如图16为逆行轨道两种扫描方式最短遍历时间减顺行轨道最短遍历时间的结果，大部分大于零。

3)逆行轨道自东向西扫描方式单星遍历时间最短为8.87 h，一天最多遍历2次，获取目标2个观测弧段；顺行轨道双星遍历时间最短为5.51 h，一天可以遍历4次，获取目标4个观测弧段。即逆行轨道相比顺行轨道，无明显优势，考虑逆行轨道的发射难度，天基平台宜采用顺行轨道双星星座配置，然后根据遍历时间和观测弧长的需求折中选择天基平台的姿态机动能力。

因此，在工程应用中，建议优选使遍历时长不超过6 h的姿态机动能力，以保证双星星座1天可对同步带目标进行不少于4次遍历，其可行解分布如图17所示。从图17可以看出，其姿态机动范围和姿态机动速度的可行解位于71°≤β≤90°, 1.9°/min≤ωAtt≤3°/min的区间内。

3 观测效能分析

3.1 观测导引律设计

考虑顺光观测需求，设定双星星座中每颗卫星都采用如图18所示的扫描方式：位置A和位置1相对太阳矢量对称；卫星位于位置A时，探测相机视轴位于最东边界，开始自东向西扫描，卫星运行至位置1时，探测相机视轴正好扫描至最西边界，实现一次完整扫描；然后从位置1开始自西向东回扫，卫星运行至位置2时，探测相机视轴与太阳光垂直，不能扫描至达到最东边界。如此往复扫描。位置A←位置B←位置C←……的扫描方式与位置1→位置2→位置3→……的扫描方式相同。

记位置A至位置1为n=0，从位置1至位置2为n=1，位置2至位置3为n=2，以此类推，由图18可以推导得到两个位置间的扫描角度Bn,扫描时间tn和卫星相对地心转过的角度θn为

(38)

公式(39)理论上表征扫描次数可趋向无穷大。但实际应用中，太小的扫描弧段应用意义不大，因此只在tn≥10 min的位置间扫描。

(39)

“位置A←位置B←……”的扫描参数与“位置1→位置2→……”相同，不再赘述。可以求得，采用这种相对太阳矢量对称的往复扫描方式，单星一天最多扫描37次(包括一次完整周期扫描和36次不完整周期扫描)，工作时间可达到18.5 h。

不同季节时间，同步带目标受光照条件不同，其观测效能结果也不同，其中夏、冬至情况一致，在夏(冬)至前后，同步带目标处于全光照；春、秋分情况一致，在秋(春)分前后，部分同步带目标会受地球遮挡处在阴影区，使得探测效率下降。因此，选择夏至和秋分两种极端工况进行仿真。

3.2 仿真结果与分析

根据第2.2.6 节的推导和结论，在顺行轨道双星星座遍历次数不少于4次的可行解中任意选择一组作为STK仿真输入的理论值，选取如表3所示。

表3 理论星座配置和观测效能Table 3 Theoretical constellation parameters configuration and its observation efficiency

根据第3.1节设计的观测导引律，对390颗同步带目标进行STK仿真。结果表明，双星星座每天探测次数不少于4次的目标个数分别为：夏至367颗，秋分355颗。双星星座并不能对所有390颗目标每天遍历4次。这是由于第2.2.6节假设相机全视场角为3°，390颗目标中倾角超过半视场1.5°的是126颗。显然，这126颗目标均可能在某些时段出现每天探测次数小于4次的现象，不同时间段对应不同的目标数量。本次仿真得到探测次数小于4次的目标共有42颗，均为倾角超过相机半视场的情况，如表4所示。因此，仿真结果符合理论推导情况。

第3.1 节表明，秋(春)分前后的探测效率低于夏(冬)至。STK仿真中，夏至和秋分工况下每天探测次数均不小于4次的同步带目标有348颗，对这348颗目标两种工况下的探测次数进行对比，如图19所示。从图19可以看出，夏至的探测次数总体高于秋分，具体来说：夏至比秋分对348颗目标的探测次数平均高3.38次；348颗目标中，319颗目标的探测次数夏至比秋分高，与预期一致。

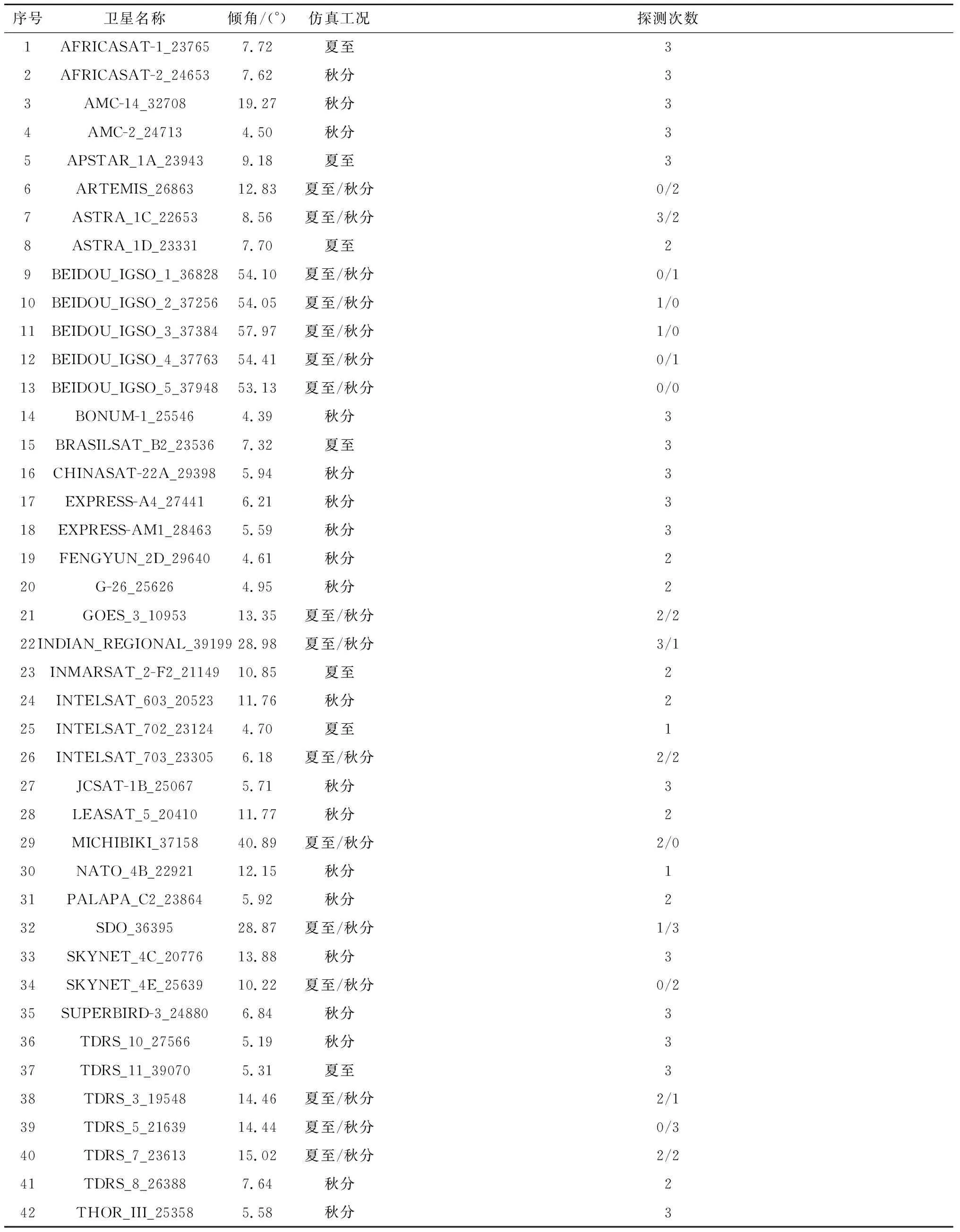
表4 探测次数小于4次的目标统计Table 4 GEO objects with detection times less than 4

4 结 论

本文对高轨天基监视星座执行同步带目标探测任务遍历效能、星座轨道部署和探测相机扫描方式之间的关系进行了研究。理论推导表明，天基平台采用顺行轨道、探测相机采用自西向东或自东向西姿态扫描方式，其姿态机动范围和速度的可行解更多，星座规模更小、观测弧长更长、遍历时间更短。设计了相对太阳矢量对称往复扫描导引律，STK仿真结果表明，在夏至和秋分工况下，双星星座对轨道倾角不大于相机半视场的所有同步带目标进行无缝遍历，且每天探测次数不小于4次，观测弧长不小于1 min。本文充分考虑了实际观测需求和工程约束，可为高轨目标监视系统的构建提供设计依据。