AOS空间通信系统中自适应帧生成算法
刘立士,田 野,徐 野,付 钰,赵晓曦
(沈阳理工大学,沈阳 110159)
0 引 言
空间数据系统咨询委员会 (Consultative Committee for Space Data Systems, CCSDS)自成立以来逐步建立了一套基本的空间通信标准。其中,高级在轨系统协议(Advanced Orbiting System, AOS)通常用来实现空-地、空-空等双向传输不同种类和特性的空间数据,被广泛的应用于空间通信领域[1-3]。该协议采用包信道复用和虚拟信道复用两层复用机制实现多用户动态共享同一物理信道[4-5],以提高空间数据信道的利用率。
在包信道复用中,通常可以采用三种帧生成算法:等时帧生成算法[6]、高效率帧生成算法[7]和自适应帧生成算法[8]。文献[9-12]对帧生成算法的性能参数进行了研究,得到一定的理论成果。但上述结论都是在泊松流模型下,针对无限缓存而得出,没有考虑提取帧所花费的时间。越来越多的研究表明[13-16],泊松流的短相关性已经不再适合现有的网络流量特性,取而代之的是自相似流量模型[17-19]。而在自相似流量模型的研究中,文献[20]对于等时帧生成算法进行了初步研究,得到复用效率的计算公式。文献[21]对文献[16]提出的模型进行细致分析,利用复合泊松过程,得到数据包到达概率分布,并对高效率算法的性能进行了研究。但是关于自适应帧生成算法的研究目前仍然比较少。文献[22]提出一种基于小波神经网络业务流量的自适应帧生成算法,相比等时算法,复用效率有所提升,同时避免高效率算法的可能长时延迟问题。但该算法重点在仿真实现,没有进行严密的理论分析。
针对以上问题,本文在自相似流量模型下,对AOS空间通信中的自适应帧生成算法进行全面研究。在有限缓存的限定下,规定了帧提取时间,分析了算法的缓存溢出情况,给出了该算法的缓存溢出概率的分布。并对该算法的性能进行分析,选取帧复用效率和包时延两个最能影响算法性能的参数指标,通过严格的理论推导,得到上述参数的理论计算公式。理论分析和仿真结果都支持了理论公式的正确性。这为AOS空间通信应用提供理论支持。
1 包到达模型
在模拟自相似流量时,ON/OFF 模型由于物理意义明确,有利于理解网络流量的自相似性产生的原理,而且计算复杂度小,得到广泛的应用。本文采用文献[16]建立叠加一类Pareto分布构成的ON/OFF模型。假设有M个ON/OFF信息源相互独立,每一个信息源都存在两种状态,分别为活跃的(ON状态)的或者是空闲的(OFF状态)。在活跃期,信源持续匀速发送数据包。在空闲期,信源不发送数据包。活跃期的长度,即信源发包时间τ服从一种Pareto分布,即P(τ=l)=cl-α,l≥1,c为常数。当M→∞时,通过叠加Pareto分布,生成渐进自相似流量。文献[21]进一步分析,发现在时刻t到达的数据包的个数由活跃期的个数ξt与活跃期的长度τ以及信源发包速率R共同决定。这里ξt=X1+X2+…+XN(t),其中Xi(i=1,2,…,N(t))表示第i个活跃期开始时刻对应的活跃期的个数,是独立同分布于参数为λ的泊松分布的随机变量。{N(t),t≥0}表示(0,t]内活跃期开始时刻处于发包状态的信源个数,服从强度为λ的泊松过程。若记(0,t]内到达的数据包数为Φ(0,t),则有[21]
(1)
特别地,在任意长度为a的时间段[s,s+a]内,到达n个数据包的概率为[21]
(2)
2 自适应帧生成算法缓存溢出概率
2.1 理论分析
自适应帧生成算法的包信道复用处理过程如图1所示。设MPDU包区长度为N,设置成帧时间的最大值,即门限值为Th。若成帧时间未到Th而当前累计的数据包数已达到N,就开始提取一帧;若成帧时间到达Th,但累计的数据包数仍不足N,则补充空数据包填满MPDU包区后开始提取一帧。提取一帧的时间设定为Te,每一帧提取后开始帧生成过程并释放。
第一帧提取过程中缓存溢出概率为
(3)
其中k=Φ(0,Th)。P(Φ(0,Th)≤N)是在成帧门限值Th内到达N个数据包的概率,由式(1)叠加得出。

(4)
1)缓存剩余包个数φj-1≥N时,第j个帧开始提取。在提取时间Te内到达的数据包个数为Φ(Te),则当Φ(Te)≤B-φj-1时缓存不会溢出。有
(5)
这里P(Φ(Te)=n)由式(2)确定。
2)缓存中剩余包个数φj-1 (6) 3)缓存中剩余包个数φj-1 (7) 综上所述,第j个帧提取过程中缓存溢出的概率为 (8) 利用MATLAB仿真软件来验证前面所推导出的理论公式与实际网络流量情况相符程度,其参数设置情况如下: 平均包到达率λ为0.8,其指数分布参数μ=1/λ,gprnd(X,K,σ,θ)为Pareto分布函数,其参数设置情况为X=0.2,K=0.5,σ=θ=1,其中,K与形状参数α相互对应,由H=(3-α)/2,可知自相似业务流的Hurst系数为0.75。缓存溢出概率随缓存容量的变化关系如图2所示。 图2给出了当Th=7 s,Te=3 s时,缓存溢出概率与缓存容量之间的关系。图中看出,随着缓存容量的增大,其溢出概率逐渐减小,而且,当缓存容量增大到一定程度,溢出概率减少变得非常平缓,所以单纯增大缓存容量对于减少溢出概率意义不大。理论值曲线与仿真值曲线误差很小,最大误差不超过5%,在缓存容量达到14之后基本重合,有力地说明了理论公式的正确性。 在门限值Th下,每个帧的MPDU复用效率为: (9) 其中SW为帧生成时间,n为在SW时间内进入缓存的包数。 第一个帧的MPDU复用效率均值E(η1)为 (10) 第j(j=2,3,…)个帧的MPDU复用效率均值E(η(j))为: (11) 1)缓存中剩余包个数φj-1=N,N+1,…,B的条件下,第j个帧的复用效率都是1,所以有 (12) (13) 3)缓存中剩余包个数φj-1=0,1,…,N-1,而第j个帧在门限值Th时刻释放,此时缓存中的包个数小于N,剩余缓存容量为B-k-φj-1(k为Th时间段内进入缓存包数),这时相应的复用效率是 P(Φ(Th)=k)·(k+r) (14) 将式(12)、(13)与(14)代入式(11),得到第j个帧的MPDU复用效率均值为 (15) 本节仿真参数设置情况与2.2相同。 图3给出了B=18,Te=3 s时,MPDU复用效率随门限Th变化的理论曲线与仿真曲线。二者拟合良好,最大误差在4%以内。当门限值增加时,复用效率先是急速增大,然后增大变慢而趋于平缓。原因是Th变大使得释放的数据帧中有效数据比例增加,复用效率增大明显。当Th到达一定数值时,Th时间内进入缓存的包数超过缓存容量,开始产生溢出,缓存多处于占满状态中 ,释放的帧中基本不用填充空闲包,复用效率接近为1。所以合理设置门限值,可以提高MPDU复用效率。 图4给出了B=18,Th=7 s时,MPDU 复用效率与随帧提取时间Te的关系。图中理论曲线和仿真曲线误差很小,最大误差在5%以内,说明了理论公式的正确性。同时还可以看出,随着帧提取时间的增长,复用效率先增大后趋于稳定,但是考虑到增大帧提取时间会增大缓存溢出概率,所以需要合理设置帧提取时间,综合提高算法的性能。 自适应帧生成算法所生产的数据帧,按照在门限值之前释放和在门限值时刻释放分为两类。所以,可以把自适应帧生成算法看作是等时帧生成算法(在Th时间内缓存中数据包数量不足N)与高效率帧生成算法(在Th之前已经到了N个数据包)的一种联合叠加机制。 假设有两个事件: A={Th内到达的包数小于N}= {第N个包到达的时间大于Th}, B={Th内到达的包数大于等于N}= {第N个包的到达时间小于等于Th}, 有 P(A)=P(Φ(Th) (16) 设每一帧的包时延为Td,则有 E(Td)=E(E(Td|Y))=P(Y∈A)· E(Td|Y∈A)+P(Y∈B)E(Td|Y∈B) (17) 其中E(Td|Y∈A)为自适应算法中对应于等时算法的平均包时延[23] (18) 这里aτ=E(τ)为公式(1)中的Pareto分布的均值。而E(Td|Y∈B)为自适应算法中对应于高效率算法的平均包时延[21] (19) 其中Pover为高效率算法下的缓存溢出概率[21]。 将式(18)和(19)代入式(17), 得到自适应算法的平均包时延为: (20) 本节仿真参数设置情况与2.2相同。 图5给出了出当B=18,Th=7 s时,平均包时延随门限值变化的理论曲线和仿真曲线,二者拟合良好,最大误差不超过3%,充分说明了理论公式的正确性。还可以看出,随着门限值的增大,其平均包时延也随之增大并且逐渐趋于稳定,当门限值增大到一定程度,趋于高效率算法的平均帧生成时间时,自适应算法将退化为高效率算法。 图6给出了B=18,Te=3 s时,平均包时延随帧提取时间变化的理论曲线和仿真曲线。二者基本重合,这表明理论模型很好地刻画了有限缓存下考虑帧提取时间的包复用过程。还可以看出,随着帧提取时间的增大,其平均包时延也随之增大,基本成线性变化。仿真结果与理论分析基本一致,充分说明理论公式的正确性。 在流量到达已经确定,即相应的仿真参数设置不变的情况下,有限缓存B、帧提取时间Te与门限值Th的设置会对仿真结果造成影响。性能良好的自适应算法应该有较小的缓存溢出概率、较高的MPDU复用效率以及较小的平均包时延。首先,减少缓存溢出是第一位的,所以优先确定有限缓存B。从图2可知,依靠无限提高缓存容量达到降低缓存溢出概率是不可取的,在2.2的仿真参数设置下,缓存容量B=18就足够满足要求。其次,在缓存容量已经确定的情况下,确定门限值与帧提取时间。为提高MPDU复用效率要增加门限值,但是门限值变大的同时,平均包时延也随之增大。另一方面,为减小平均包时延,需要减少帧提取时间,但相应的复用效率也随之降低。因此,只能有所取舍,在确保复用效率的前提下,尽量减小时延。为此,本文以高效率算法为比照,通过大量的仿真实验,结果如图7与图8所示,在B=18时,取Th=7 s,Te=3 s比较恰当,此时自适应算法体现出较高的复用效率(0.97),接近高效率算法。若此时增大门限值,复用效率提升不明显,但是平均包时延的增加非常剧烈。同时,自适应算法体现出较小的平均包时延(4.7 s),整体低于高效率算法。若此时减小帧提取时间,平均包时延的减小比较平缓,但是复用效率的降低变得剧烈。 本文在自相似流量模型下,对AOS空间通信中的自适应帧生成算法进行了研究。在设置了有限缓存和帧提取时间的基础上,得到了缓存溢出概率的递推公式。然后对自适应算法的性能进研究,选取最能体现算法性能的参数指标,通过严格的理论推导,得到了MPDU复用效率与平均包时延理论计算公式。该成果可以为AOS空间通信系统的实际应用提供一定的理论支持。本文得到如下一些结论: 1)在有限缓存下,不能依靠无限增大缓存容量达到降低缓存溢出概率的目的。 2)在门限值给定的情况下,自适应算法可以视为高效率算法与等时帧生成算法的叠加,在门限值趋于高效率算法的平均帧生成时间时,自适应算法将退化为高效率算法。 3)恰当地设定门限值与帧提取时间,可以有效提高自适应帧生成算法的性能。2.2 仿真结果
3 自适应帧生成算法的MPDU复用效率
3.1 理论分析
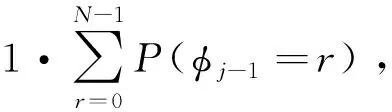
3.2 仿真结果
4 自适应帧生成算法的平均包时延
4.1 理论分析
4.2 仿真结果
5 提高自适应帧生成算法性能的参数设定
6 结 论

