利用遥测数据评定防空导弹杀伤目标性能方法
刘鸿雁,胡 悦
(92941部队,辽宁葫芦岛125000)
要提高防空导弹杀伤目标的性能,除了提高制导精度和武器系统的可靠性等因素外,主要取决于引信与战斗部的配合效率。由于目标的机动、制导与控制系统的随机误差等,在全方向攻击空中运动目标和有严重干扰的环境下,导弹直接命中目标的概率很低,所以大多数防空导弹都采用近炸引信[1],利用导弹制导控制系统提供给引信的相关信息,如导弹-目标相对速度、导弹-目标视线与弹轴夹角等,按照一定的计算模型,尽量使引信启动区与战斗部的动态杀伤区相重合[2]以提高引战配合效率及杀伤目标能力。
靶场飞行试验中,通常利用靶标模拟防空导弹真实目标。受靶标近场反射特性、引信启动概率、靶标易损性等综合因素的影响,在导弹满足系统制导精度的情况下,对目标的杀伤存在一定概率,因而有必要研究试验结果评定。本文从弹目遭遇段相对运动关系及多普勒引信工作原理出发,利用靶场遥测数据,对综合评定导弹杀伤目标性能方法进行了研究。
1 计算模型
在弹目遭遇段,可以认为导弹和目标之间做匀速直线运动,即弹目相对速度vr为常数[3-5]。如果将导弹和目标看作点目标[6-8],在弹体坐标系下导弹和目标的相对位置关系如图1所示。图中,vr为目标与导弹的相对速度,v0为战斗部破片静态飞散速度,v1为战斗部破片动态飞散速度[9],Ri为弹目视线,θi为弹目视线与相对速度夹角,θz为最佳启动角,ρ为脱靶量,Ωr为相对速度与弹轴夹角,Ti、Tz分别表示目标相对导弹运动过程中的2个位置。

图1 导弹和目标遭遇相对位置关系示意图Fig.1 Diagram of relative relation between missile and target
1.1 频率启动计算模型
引信最佳多普勒频率启动工作原理见图1。可见,在一定的交会姿态下,当目标沿着相对速度vr进入引信探测视场时,弹目视线与相对速度夹角θi不断变化,对应的多普勒频率也将随之变化,可表示为:
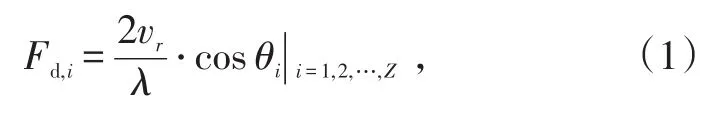
式中,λ为引信波长。
当导弹沿相对运动轨迹运动时,θi由小变大,Fd,i由大变小。通过脱靶点后,Fd,i改变符号,并逐渐增大。当θi变化到θz时,弹目视线恰好与战斗部破片动态飞散角中心方向(v1方向)重合,显然此时就是引爆战斗部的最佳时刻,对应的多普勒频率Fd*定义为最佳多普勒频率。Fd*可以根据模型计算得出并预先装定,在弹目交会时,引信探测到目标并连续测量多普勒频率,只要在测得频率为Fd*时给出启动信号,就可以保证引战配合的最佳效果。
在工程应用中,为提高引战配合效率,使用了脱靶方位识别[10-11]及启动角修正技术[12]。即在模型中对导引头提供的制导信息,如相对速度、天线转角及角误差等信息处理后,按一定数学算法进行脱靶方位识别。模型中,对导引头制导信息的处理主要包括:制导信息转换、信息有效性判断、角速度信息的噪声滤波以及信息利用的起点和固化时刻的判定等。然后,在计算最佳启动角时引入脱靶方位的修正,消除不同脱靶方位的“频率模糊”[13],以确定该方位最优的启动角。这样的设计实现了启动角随脱靶方位进行修正的目的,提高了引战配合效率。
1.1.1 相对脱靶方位角ωr计算模型
相对速度与导弹纵轴夹角为:
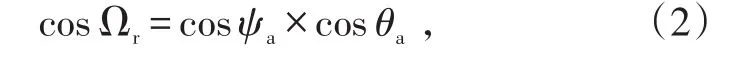
式中,ψa、θa为导引头天线的2个转角。
相对速度在弹体坐标系内的方位角为:
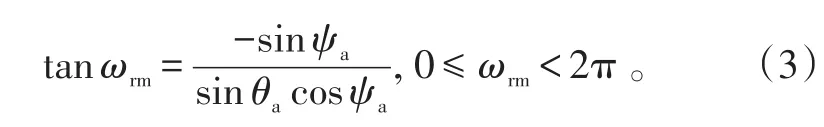
目标在弹体坐标系内的方位角为:

式(4)、(5)中:ωa为导引头测量的弹目视线旋转角速度在弹体坐标系中的方位角;ωy、ωz为弹体坐标系中导引头角速度矢量的2个分量。
由式(2)~(5)可知,相对脱靶方位角为:

1.1.2 最佳多普勒频率Fd*计算模型
导引头测量的相对速度值为:

式(7)中:Fda为导引头测量的多普勒频率值;λa为导引头波长。
战斗部破片在相对速度坐标系[14]中的动态飞散中心方向角为:
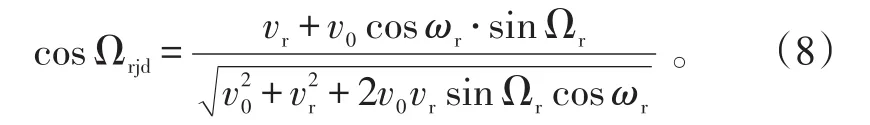
综上可知,最佳多普勒频率为:

1.2 延时启动计算模型
在实际应用中,由于体目标效应[15-17]的影响,引信输出的多普勒频率信号不是光滑的曲线,频率值会有起伏。图2给出了引信多普勒频率变化的一个实例,可见,实际曲线并非理论曲线那样平滑规则。故上述最佳多普勒频率启动原理的运用,必须考虑到引信测量的多普勒信号可能不连续,如果单纯使用频率启动原则,引信或许不能适时启动。因此,在工程模型中,还采用了引信启动延时自适应调整技术[18]。当引信测量的多普勒频率信号不连续或丢失时,依据断点前的频率信号和预先装定的最佳多普勒频率值,按照一定的算法计算延迟时间,形成最佳多普勒频率与延迟时间的双通道自适应启动准则,确保引信适时启动。
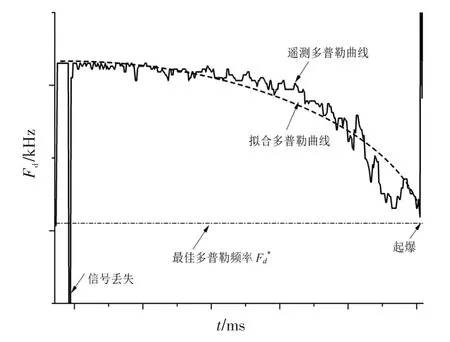
图2 频率启动引信多普勒频率变化曲线Fig.2 Variation curve of frequency start-up of fuze doppler frequency
图3为引信延时启动的多普勒遥测曲线,在达到最佳多普勒频率门限前信号丢失时,引信按照延时启动准则启动。延迟时间计算模型分为“距离一点法”和“频率两点法”。
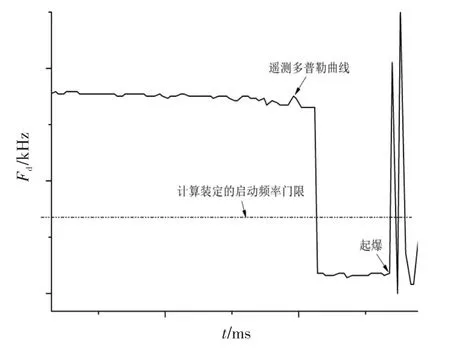
图3 延时启动引信多普勒频率变化曲线Fig.3 Variation curve of delay time start-up of fuze doppler frequency
1.2.1距离一点法模型
在相对速度坐标系下,距离一点法计算原理如图4所示。
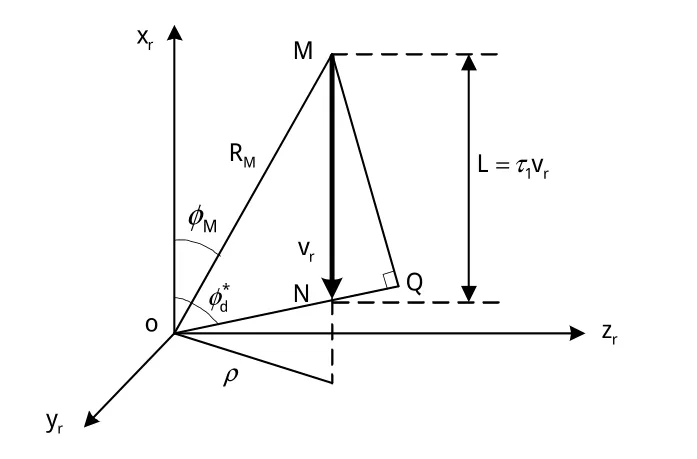
图4 距离一点法计算原理图Fig.4 Diagram of one point of distance
当目标沿着相对速度方向进入引信天线波束时,假设在任意点M引信输出的多普勒频率值为Fd1,其对应的弹目视线与相对速度的夹角为φM、弹目距离为RM;若装定的最佳启动多普勒频率为Fd*,其对应的弹目视线与相对速度的夹角为、目标在相对速度方向的位置为N;显然,目标从M点至N点的运动时间就是延时启动时间τ1,则由图4中对应关系可知:

式中,

由式(10)~(12)可知:
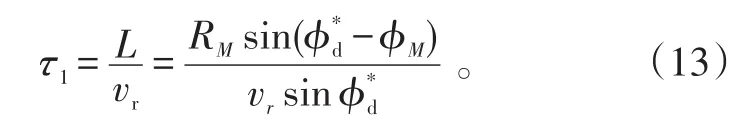
式(13)中,RM可利用引信距离波门信息来确定。
1.2.2 频率两点法模型
当引信不能提供距离信息时,使用频率两点法模型,在相对速度坐标系下,计算原理见图5。
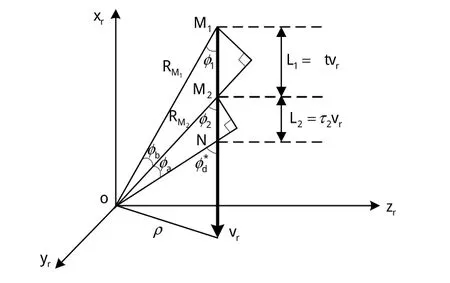
图5 频率两点法计算原理图Fig.5 Diagram of two points of frequency
当目标沿着相对速度方向进入引信天线波束时,假设在任意点M1引信输出的多普勒频率值为Fd1,其对应的弹目视线与相对速度的夹角为φ1;在M2点引信输出的多普勒频率值为Fd2,其对应的弹目视线与相对速度的夹角为;若装定的最佳启动多普勒频率为Fd*,其对应的弹目视线与相对速度的夹角为;显然,目标从M2点至N点的运动时间就是延时启动时间τ2,则由图5中对应关系可知:
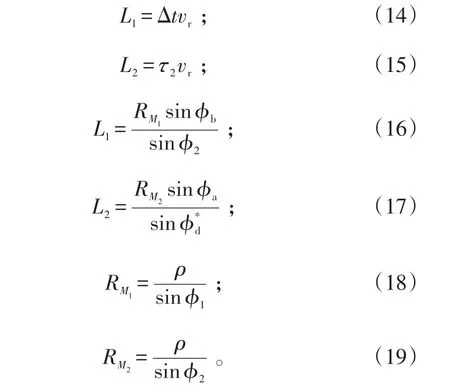
由式(14)~(19)可得:

式中,Δt为测量Fd1~Fd2的时间间隔。
2 计算算例
表1~3分别给出了利用频率启动和延时启动的计算结果。
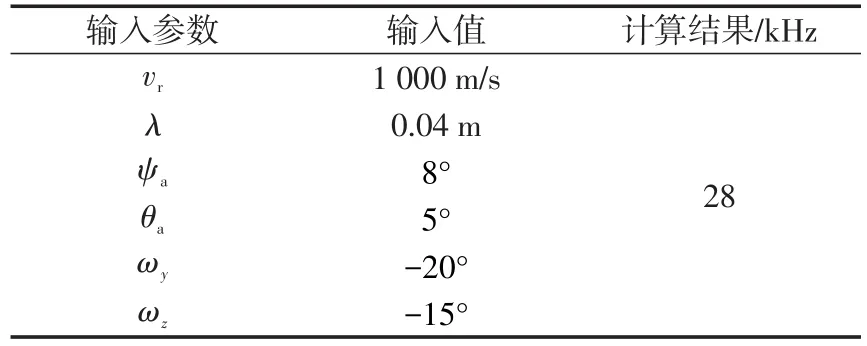
表1 频率启动计算结果Tab.1 Computing result of frequency start-up

表2 距离一点(τ1)启动计算结果Tab.2 Computing result ofτ1start-up
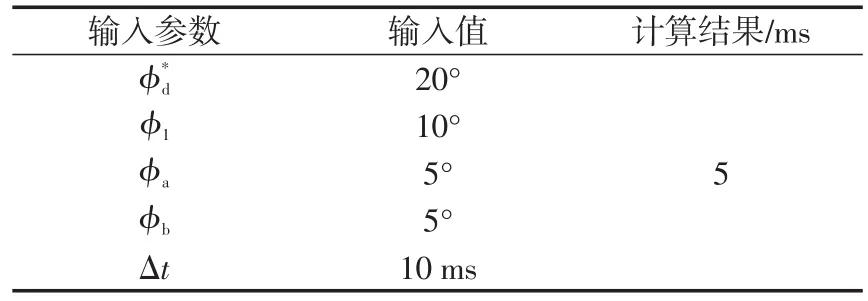
表3 频率两点(τ2)启动计算结果Tab.3 Computing result ofτ2start-up
3 误差分析
表1~3中的输入参数为系统设计已知或是从飞行试验数据中获取,利用上述公式,就可以总体上判断引信频率启动或延时启动功能是否正常。但在实际应用中,存在一定的误差因素。
频率启动参数判定误差范围主要考虑:
1)遥测系统测量误差;
2)由于遥测信号采样率不同,导致信号之间不同步而产生的误差;
3)在引信启动时刻,不能将启动当帧信号及时送到遥测而产生误差;
4)引信多普勒频率测量精度产生的误差。
延时启动参数判定误差范围主要考虑以上1)~3)点以及信号处理时间产生的误差。
4 结论
本文根据防空导弹弹目遭遇段相对运动关系以及多普勒引信工作原理,推导出利用飞行试验遥测数据判定引战配合及导弹杀伤目标功能正常的方法,给出算例对频率启动、距离一点法及频率两点法延时启动进行了计算并对主要误差影响因素进行了分析。
应当指出,判定引战配合及导弹杀伤目标功能正常的方案和模型不是唯一的,从引信和制导系统取得的信息形式不同,方案和模型也不同。利用试验外测结果对以上遥测数据计算结果进行对照和检验,证明本文给出的计算方法和结果正确可行,可以为防空导弹飞行试验结果的分析与评定提供支持。

