大入射余角海杂波相关特性分析及幅度拟合
刘恒燕,宋 杰,熊 伟,崔亚奇,吕亚飞
(海军航空大学,山东烟台264001)
海杂波背景下的目标检测一直是检测的重点问题。由于实际目标检测时,不可能像计算机仿真数据一样事先知道目标及杂波的幅度分布参数、相关特性及阶段特征,而设置合理的检测门限则要求雷达必须根据实际遇到的情况调整计算方式。因此,预测雷达检测时最可能遇到的情况以及这些情况对于多样雷达系统参数的依赖性和最可能的时空变化率,对于提高检测概率、提高检测算法的性能具有重要意义[1-4]。由于传统CFAR算法的设计依赖于海杂波特性研究,如时间维滑窗的选择依赖于海杂波的时间相关性,距离维滑窗的选择依赖于海杂波的空间相关性。因此,关于海杂波特性的研究如时间相关性、空间相关性及海杂波统计分布特性也在一直深入研究。但由于实际应用条件限制,大部分研究集中在高分辨率低入射余角条件下。随着雷达搭载平台的不断发展,高分辨率大入射余角情况下的目标检测问题也逐渐受人关注。Jakeman和Pusey认为,随着雷达分辨率的提高,每个分辨单元内的散射体数量为服从泊松分布的随机变量,如果该均值服从Gamma分布,则杂波服从K分布[5]。2014年Luke Rosenberg等人研究了中入射余角X波段雷达的幅度统计特性,发现K分布无法更好拟合高分辨率大入射余角(HGA)海杂波的海尖峰特性,尤其是大能量海杂波带来的长拖尾特性。为了使分布模型更好地拟合实测数据中多余的瑞利部分,提出了K+R、K+N、P+N模型,并给出其参数估计方法——矩估计法。通过CCDF验证了K+R模型可以有效拟合实测数据中的多余Rayleigh部分,在大入射余角海杂波背景下具有近乎完美的拟合效果且可有效避免KA分布等复杂分布的多参数估计问题。但由于K+R模型参数估计需要计算前三阶矩,计算量较大且无闭合表达式,并未在检测算法中得到推广[6-10]。
1 海杂波特性
1.1 时间相关性
1.1.1 定义
时间相关性表明了海杂波在时间维的相关性强弱,直接影响了CFAR算法时间滑窗中单元个数的选取,如时间相关性强,所需单元个数增多。时间相关性采用归一化时间自相关函数来衡量,表达式为:
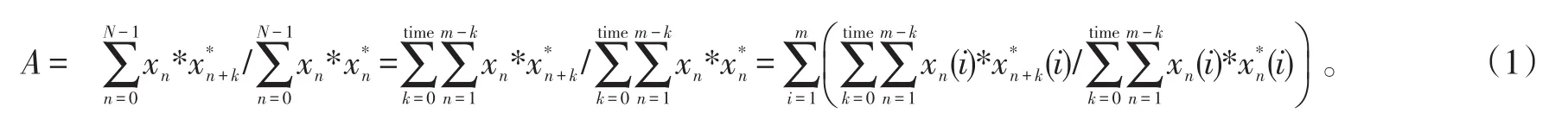
式(1)中:xn是接收信号的复数形式;为其共轭。
1.1.2 实测数据仿真结果
本次实验实测数据为水平极化ku波段雷达在风平浪静的海面上采集,即低海况等级。距离分辨率为1.875 m,每个脉冲采样204 8次,每次采样间对应一个距离单元,为0.281 25 m。
海杂波的时间相关性如图1、2所示,每个圆圈代表0.2 ms,曲线第1次与1/e相交的点对应的横坐标即为相关时间,若相交点在2个圆圈之间,则相关时间在上一个圆圈基础上多0.1 ms,图1、2的相关时间分别为0.1 ms、0.7 ms。
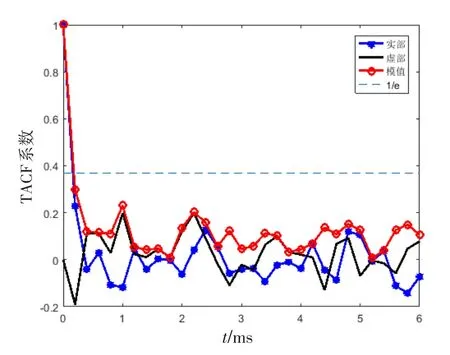
图1 第5组目标单元时间相关性示例Fig.1 Example of temporal correlation
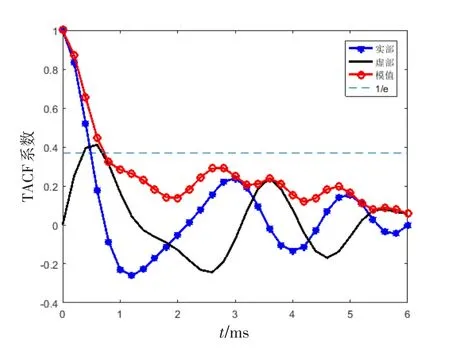
图2 第6组目标单元时间相关性示例Fig.2 Example of temporal correlation
44°入射余角到74°入射余角时间相关性统计如表1~4所示。

表1 44°入射余角下不同距离单元的相关时间Tab.1 Correlation time of different distance units at 44°grazing angle ms

表2 59°入射余角下不同距离单元的相关时间Tab.2 Correlation time of different distance units at 59°grazing angle ms

表3 69°入射余角下不同距离单元的相关时间Tab.3 Correlation time of different distance units at 69°grazing angle ms

表4 74°入射余角下不同距离单元的相关时间Tabl.4 Correlation time of different distance units at 74°grazing angle ms
表1~4中:44°入射余角相关时间均值为2.4 ms;59°为 3.2 ms;69°为 3.0 ms;74°为1.5 ms。这说明从入射余角44°到74°,随着入射余角增加,海杂波时间相关性先增加后减小,时间相关性最强的入射余角在60°左右。
1.2 空间相关性
1.2.1 空间相关性定义
空间相关性定义为雷达径向或方位向上两个分离的海面距离单元反射信号的相关性[11-13],表明了海杂波在空间维的相关性强弱,直接决定了CFAR算法中距离向滑窗的选取。此时,采样点间对应的时间间隔通常在微秒量级以下,时间相关性可忽略,实测数据采集过程中方位向变化在1°以下,方位向空间相关性可忽略不计,仅考虑径向距离单元的空间相关性,采用海杂波平均反射率的归一化空间自相关函数表示:
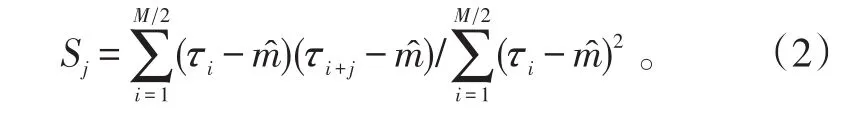
海杂波的空间相关性如图3、4所示。每个圆圈代表一个距离单元,曲线第一次与1/e相交的点对于横坐标即为相关距离单元个数,如图3所示,相关距离单元个数为1个,由于大部分相关距离单元在20个以内,横坐标最大值为20,图4的情况记为20+,实际计算时按照20个进行计算。
44°入射余角到74°入射余角时间相关性统计如5表所示。表5表明,在44°到74°入射余角间,随着入射余角的增加,平均相关距离单元个数增加,这就意味着当入射余角增加,检测目标需要获得比低入射余角更多的距离单元。

图3 空间相关性示例Fig.3 Example of spatial correlation
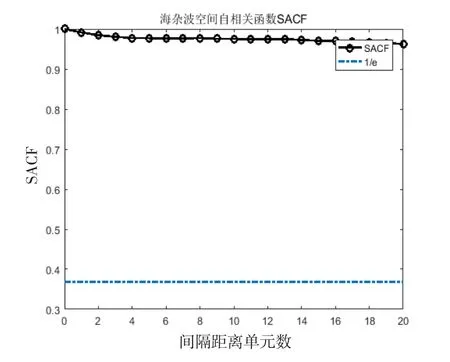
图4 空间相关性示例Fig.4 Example of spatial correlation
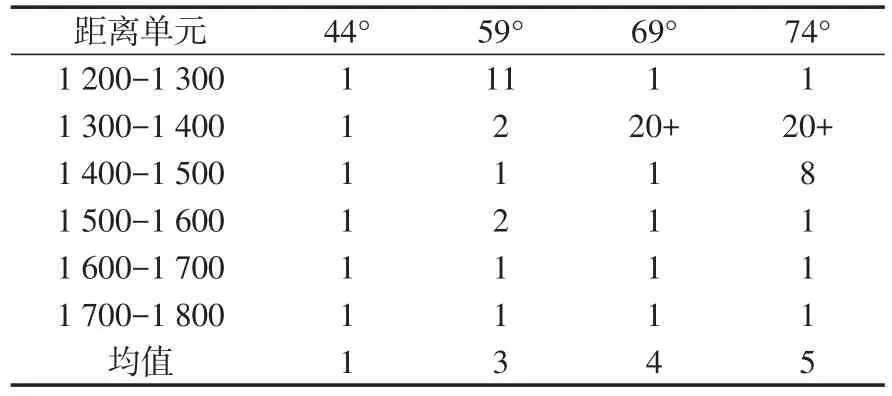
表5 不同入射余角下相关距离单元长度Tab.5 Correlation spatial units of different grazing angles
2 海杂波幅度拟合
2.1 海杂波幅度分布
由于Luke Rosenberg等提出的K+R模型参数估计需要计算前三阶矩,计算量较大且无闭合表达式[14],为解决这个问题,本文提出了KR模型。KR模型为Rayleigh分布与K分布组成的混合分布,其表达式为:
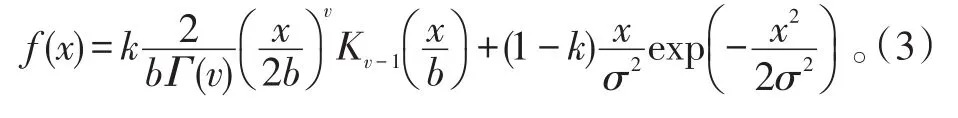
式(3)中:b为K分布尺度参数;v为K分布形状参数Kv-1(⋅)为v-1阶第三类修正贝塞尔函数;k为权重参数满足0<k<1。
式(3)的前半部分为K分布,解释了慢变化的纹理分量调制快变化的散斑分量;后半部分为瑞利分布,属于高斯模型,在点目标经典CFAR检测算法与距离扩展目标检测算法中得到了广泛应用,
2.2 实测海杂波数据拟合
分别利用KR分布、K分布、Rayleigh分布及KK分布[15-20]拟合了入射余角44°到74°之间的4组数据,为了更好描述各分布对实测数据拖尾部分的拟合效果,拟合结果除了CCDF函数外,用平均相对误差衡量,其定义式为:

定义err<0.5为有效拟合,0.5≤err≤1为近似有效拟合,err>1为拟合失效,结果如图5~8所示。参数估计结果如表6~8所示。
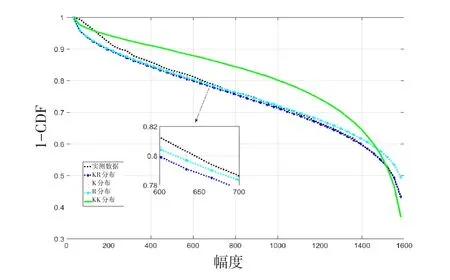
图5 44°入射余角拟合结果Fig.5 Fitting results at 44°grazing angle

图6 59°入射余角拟合结果Fig.6 Fitting results at 59°grazing angle

图7 69°入射余角拟合结果Fig.7 Fitting results at 69°grazing angle
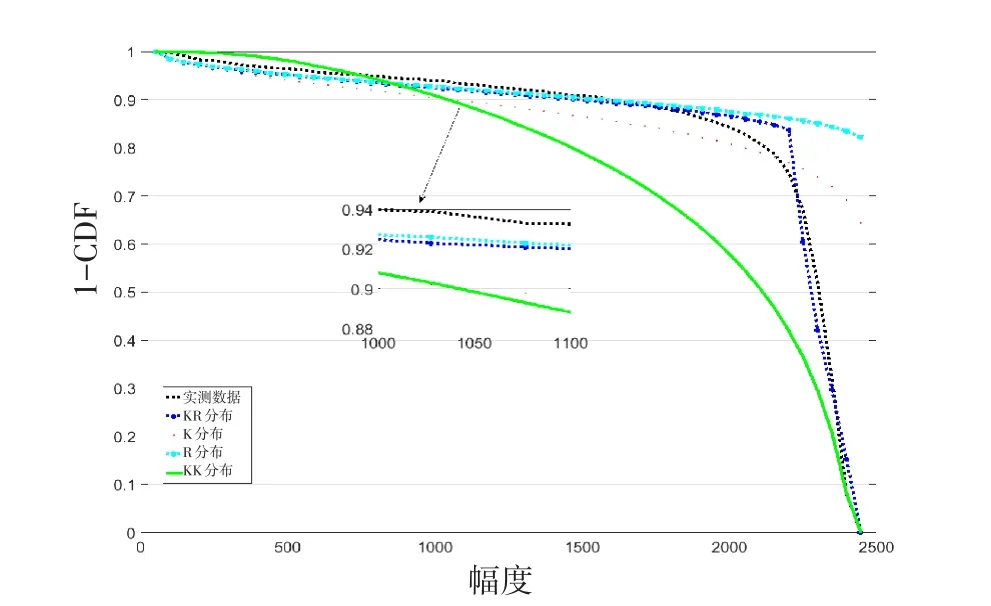
图8 74°入射余角拟合结果Fig.1 Fitting results at 74°grazing angle

表6 不同入射余角下不同分布拟合参数Tab.6 Fitting parameters of different distributions at different grazing angles

表7 不同入射余角下KR分布拟合参数Tab.7 Fitting parameters of KR distribution at different grazing angles

表8 不同入射余角下KK分布拟合参数Tab.8 Fitting parameters of KK distribution at different grazing angles
表6~8表明:入射余角44°时,KR分布、K分布为有效拟合,Rayleigh分布、KK分布为近似有效拟合,KR分布对拖尾部分拟合效果最好;入射余角59°时,KR分布、KK分布与K分布对实测数据的拟合为有效拟合,Rayleigh分布为近似有效拟合,KR分布对拖尾部分拟合效果最好;入射余角69°时,KR分布、K分布为有效拟合,Rayleigh分布、KK分布为近似有效拟合,KR分布对拖尾部分拟合效果最好;入射余角74°时,KR分布、KK分布对实测数据的拟合为有效拟合,Rayleigh分布与K分布为近似有效拟合,KR分布对拖尾部分拟合效果最好。
3 总结
海杂波相关时间维持在毫秒量级,且随着入射余角增加,先增加后减小,时间相关性最强的入射余角在60°左右,而平均相关距离单元个数一直增加。这就意味着当入射余角增加,检测目标需要获得比低入射余角更多的距离单元,而所需时间维单元则先增加,后减少。在KR分布、KK分布、Rayleigh分布、K分布对海杂波实测数据的拟合中,只有KR分布一直是有效估计,即KR分布对海杂波拖尾部分的拟合效果最优。

