一种反舰导弹纯方位射击的评价算法

王光辉，余仁波，张丽萍

（海军航空大学，山东烟台264001）

反舰导弹纯方位射击是仅有目标方位的一种射击方式[1]。发射平台的电子侦察设备利用目标的辐射信号测量目标的方位并对目标进行射击，其特点是隐蔽性好，易于对目标形成突然袭击，因而受到广泛的关注。文献[2]研究了被动定位目标的捕捉概率算法，文献[3-4]采用向目标散布中心发射的方式实施盲目射击，但需要提供目标的距离和误差分布，文献[5]研究了双舰无源定位反舰导弹捕捉概率问题，文献[6]建立了一种纯方位发射捕捉概率解析算法；但它们均没有考虑目标机动对捕捉概率的影响，而且，纯方位射击时，既没有目标的距离，也没有目标位置误差的分布。

本文研究一种反舰导弹纯方位射击的评价算法，研究多种因素对该射击方式捕捉目标效果的影响。

1 纯方位射击的原理

反舰导弹的飞行弹道分为自控飞行段和自导飞行段[7]。在自控飞行段导弹按导弹发射时刻装定的射击诸元飞行，自控飞行段结束后，末制导雷达开机搜索捕捉目标，对掠海飞行的反舰导弹，可近似认为它与目标在同一水平面上，如图1所示，OX为导弹的飞行方向，XOZ称为捕捉坐标系，扇形ABCD为末制导雷达有效搜索区，一般认为只要目标在ABCD内，即认为目标被捕捉[8-9]。

末制导雷达有效搜索区ABCD的大小用以下参数确定：OA=OD=rd1称为搜索区近界，OB=OC=rd2称为搜索区远界，∠BOC=2α称为搜索区的方位宽度。

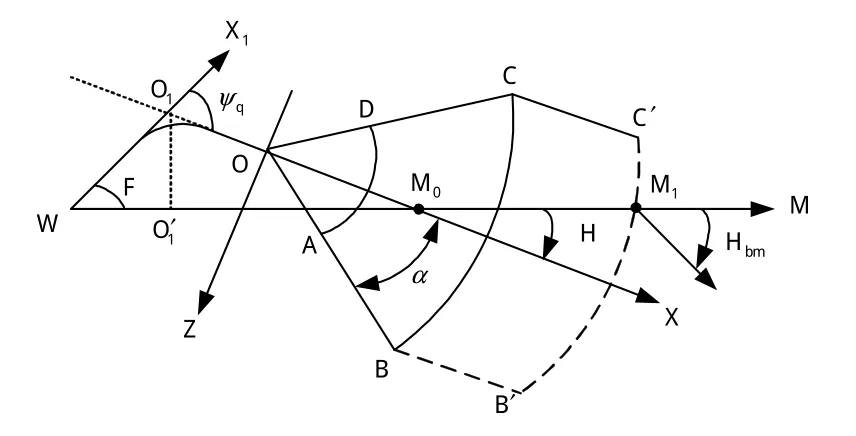
图1 方位射击示意图Fig.1 Schematic of azimuth shot

2 捕捉目标算法

研究反舰导弹末制导雷达能否捕捉到目标，必须确定目标的位置、导弹的位置和导弹的航向[10]。因为纯方位射击时，没有目标的距离，仅有电子侦察设备获得的目标方位信息（图1中的WM），因而判断捕捉目标的信息不充分。为此，可假设目标位置M1，M1肯定在电子侦察设备获得的目标方位线WM上。

设定目标位置后，还必须确定导弹的飞行方向。在实施纯方位射击时，为确保反舰导弹末制导雷达搜索尽可能大的范围，通常为目标设定一个较小的距离Rm0[2-3]，如图1中的WM0所示。图中，W为导弹发射时刻发射平台的位置，WX1为导弹发射的方向，M0为火控系统设定的目标位置，也是导弹发射前装定到导弹上的目标位置。导弹发射后，首先沿发射装置的指向WX1飞行，导弹达到巡航速度且稳定飞行后，由弹上控制系统根据导弹的实时位置和装定的目标位置M0，控制导弹转弯向M0飞行。导弹的飞行方向与目标方位线的夹角ΔH为[11]

式（1）中：F为发射角，是目标方位线与导弹发射方向的夹角；ψq为导弹前置航向角，是导弹发射方向与导弹末端飞行方向的夹角。

下面确定导弹的位置。从导弹发射起飞到导弹转向，导弹需要一个加速和稳定飞行的过程，在这个过程中，导弹的飞行距离为R0，之后，导弹以半径Rd转弯，直到导弹的飞行方向指向装定的目标位置M0，如图1中的OX所示。设导弹的发射方向与导弹转弯后飞行方向延长线的交点为O1，O1点在WM0上的投影为O′1，则在三角形WO1M0中，有：

式（2）、（3）中，RO1为O1点到M0的距离。

对一给定的导弹，其性能指标是确定的，其固有的参数是已知的，因此，在式（1）～（3）中，F、RO1、R0、Rm0和Rd是已知参数，ψq、ΔH和RO1未知。

将式（1）～（3）可改写为：

显然，式（4）～（6）是一个非线性方程组，可将其简记为：

式（7）中：

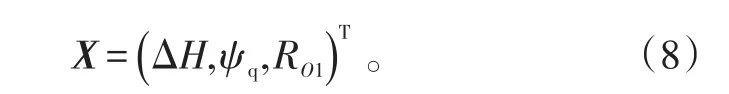
下面，证明方程组（7）有解。

当F≠0时，易证fi(X)连续可微，假设

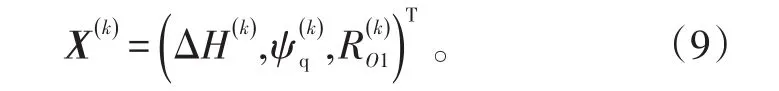
为非线性方程组（6）在第k次迭代的近似值，则其雅克比矩阵为：[12]

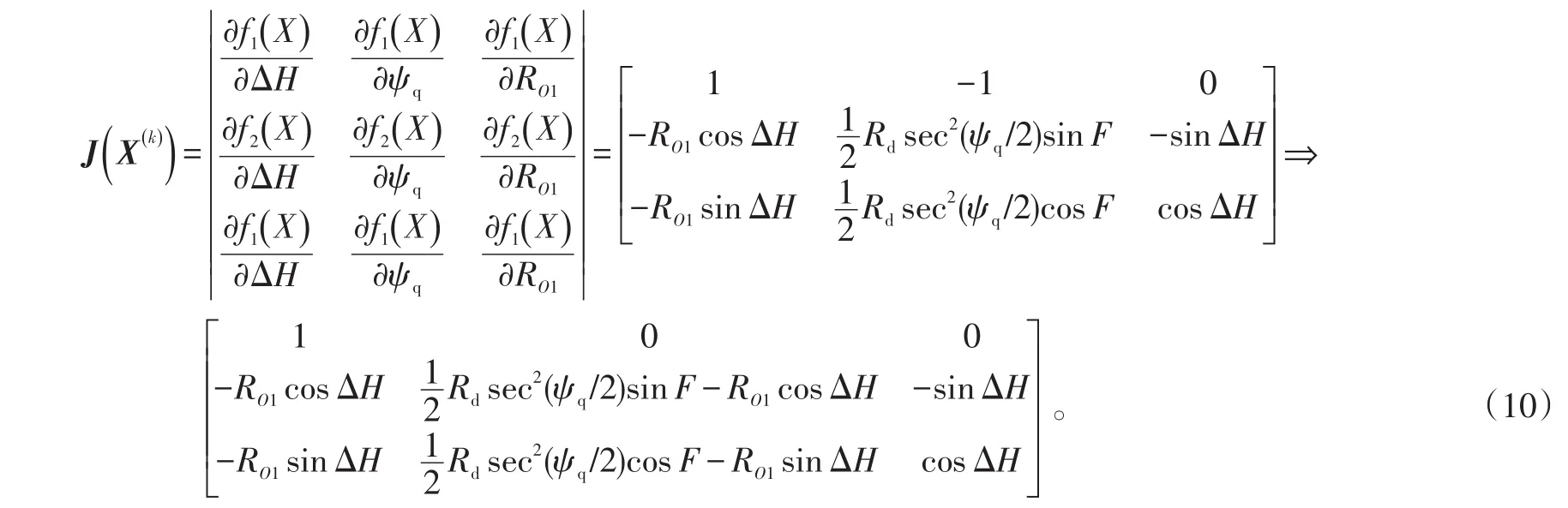
式（10）的行列式的值为：

若式（11）为0，则有ψq=2arctan(RO1/Rd)，因为RO1＞O1O′1＞Rd，即ψq＞π/2，也就是说如果ψq≤ π/2，式（11）肯定不为0，则J(X(k))为非奇异矩阵，即可采用迭代法求取ΔH、ψq、RO1。控制F的初值，即可实现ψq=F+ΔH≤π/2，实际上F、ΔH都比较小。

对方位射击而言，反舰导弹进入末端飞行航路后，末制导雷达即开机搜索目标，如图1中的O点所示，O点与M0点的距离为：

以末制导雷达开机位置O点为原点，建立捕捉坐标系XOZ，OX为反舰导弹的飞行方向，如图1所示。M1在捕捉坐标系XOZ中的坐标为：

式中，R为目标的实际距离。

末制导雷达开机时，导弹的飞行时间为：[13]

式（14）中：k为导弹转弯时的速度下降系数；Vd为导弹的巡航速度；t0为导弹加速度时间常数。

考虑到目标的机动，末制导雷达开机时，目标在捕捉坐标系的坐标为：

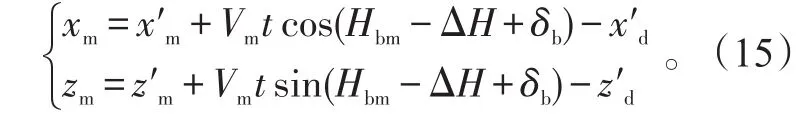
式（15）中：Hbm为目标航向与目标方位线的夹角，在目标方位线的右侧为正；δb为目标的方位误差；x′d、z′d为导弹的弹道误差，它是导弹飞行时间的函数，一般认为该误差服从正态分布且互相独立，其均方根差可用多项式表示[14]

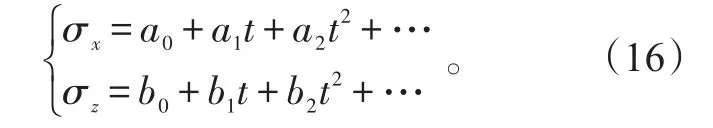
ξ1、ξ2分 别为 (0,1)均匀分布随机数序列{ξ11,ξ12,…,ξ1N} 和 {ξ11,ξ12,…,ξ1N} 的一个元素。二维正交的正态分布的随机数为：[15]

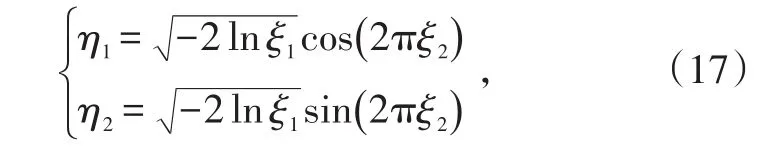
且

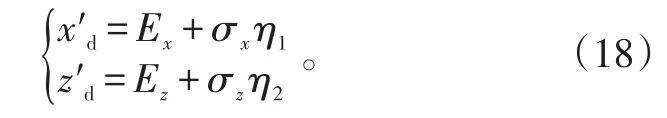
式（18）中：σx、σz分别为反舰导弹t时刻纵向和横向弹道误差的均方根差；Ex、Ez分别为反舰导弹t时刻的系统误差。

导弹的弹道误差可用导弹航向误差来表示，即

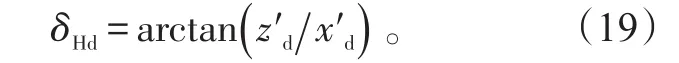
式（19）中，δHd为导弹航向误差。

3 捕捉目标判据

反舰导弹末制导雷达搜索捕捉目标的过程是一个动态过程，在末制导雷达在距离和方位上搜索目标的同时，反舰导弹继续向前飞行，捕捉坐标系XOZ随导弹的平飞平移，以末制导雷达方位搜索周期T′为时间间隔，动态更新目标的坐标为：[16]

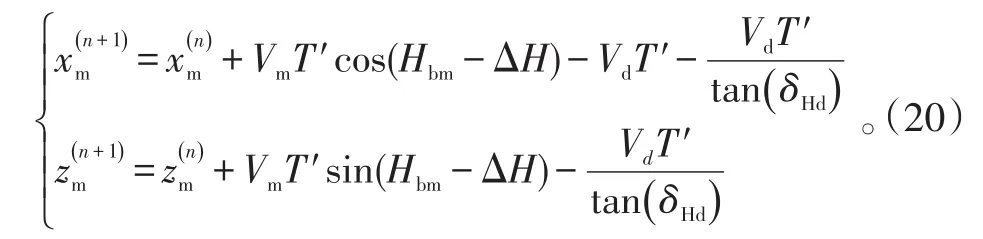
在末制导雷达第n+1个搜索周期，只要目标的坐标满足[17-18]

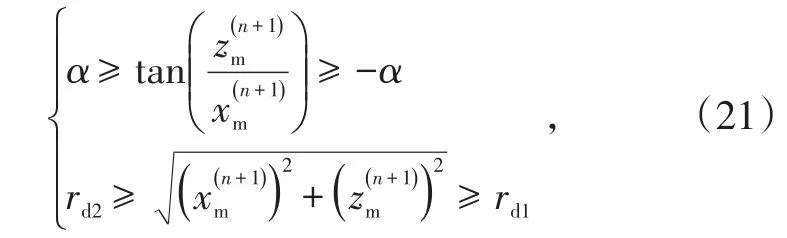
则目标被捕捉。否则，反舰导弹向前飞行的同时，继续搜索目标，直到导弹到达最大射程。

共进行N次模拟，如果有n次捕捉到目标，根据贝努利定理，当N足够大时，捕捉目标的概率近似为：

因为目标航向未知，采用目标航向在0～360°内均匀取值的方式来处理。不妨将0～360°分成I等分，目标航向有I个，目标采用第i(i=1,2,…,I)个航向被捕捉的概率为Pi，可用式（22）求得，那么，捕捉目标的平均概率为

4 举例仿真

假设相关参数分别为：rd1=1km，rd2=30km，α=40°，T′=3 s，Vd=0.3km/s，t0=3 s，R0=3km ，Rd=6km ，k=0.8 ，σx=σz=0.001t+0.000 001t2，Ex=Ez=0，δb=0。仿真结果如图2、3所示。图2是Hbm在0～360°均匀取值后，反舰导弹末制导雷达捕捉目标概率的平均值；图3是目标速度Vm=30 kn时，不同Hbm（目标航向与目标方位线的夹角）条件下的捕捉概率。图2可以看出，纯方位射击反舰导弹捕捉目标的平均概率随目标距离的增加而减小，在相同条件下，导弹的发射角越大，反舰导弹捕捉目标的平均概率越小，且目标速度越快，捕捉目标的平均概率越小。从图3可以看出，纯方位射击反舰导弹捕捉目标的概率与目标的航向密切相关，而且不同航向目标的捕捉概率差异很大，该差异随发射角的增加而增强。

图2 发射方位角对捕捉概率的影响Fig.2 Effect of emitter azimuth on capture probability

图3 目标航向对对捕捉概率的影响Fig.3 Effect of target course on capture probability

5 结论

建立的算法较真实地反映了方位射击时，反舰导弹末制导雷达捕捉目标的动态过程，较为客观地反映了多种因素对纯方位射击捕捉目标概率的影响。综合研究结果可得如下结论。

1）在实施方位射击时，导弹发射方向最好是电子侦察设备测定的目标方位。

2）当目标实际距离较远时，反舰导弹捕捉目标的平均概率较低，而且当目标采用某些航向时，捕捉目标的概率会很低。

算法没有考虑末制导雷达搜索范围内有其他目标或岛礁的情况。如果在目标方位线附近、目标之前有其他目标或岛礁，末制导雷达将捕捉其他目标或岛礁，这说明这种射击方式的风险性很大。