基于ANSOFT的电磁继电器磁路铆接设计

(厦门宏发电声股份有限公司，福建厦门，361021)

1 引言

电磁继电器的磁路的装配方式多种多样，常用的有旋铆和压铆。压铆又按铆迹分为锥铆、劈铆、花铆。从铆头加工工艺性上考虑，十字花铆是一种加工较简单的花铆形式，如图1。

磁路铆接的判定标准一般通过铆接强度、铆接扩张度、铆接深度等来量化评价铆接可靠性，另外还可以用金相切片的方式分析轭铁与铁芯的贴合尺寸来评价铆接质量。

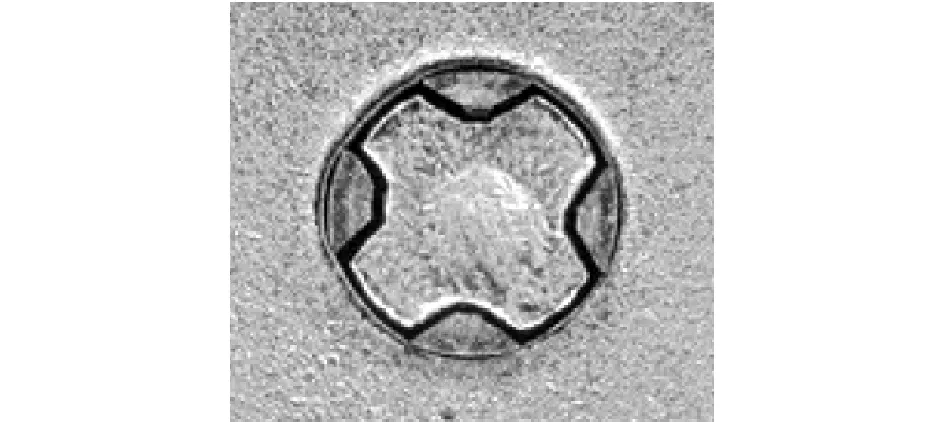
图1 十字花铆外观

金相分析时，较常出现的磁路铆接缺陷如图2所示。图2(a)中铁芯未能完全涨紧贴合轭铁面，铁芯与轭铁截面位置贴合尺寸t≈0.4mm<70%T(T为轭铁厚度1.0mm)。图2(b)中铁芯台阶面与轭铁不贴平存在δ=0.181mm轴向空隙。

图2(a)，在各类铆接工艺中均可能出现，特别是旋铆工艺，铁芯受力不足，导致铁芯与轭铁贴合深度不足。图2(b)产生的原因主要有铁芯与线圈、轭铁尺寸不匹配，或者铁芯受较大的铆接力影响产生变形，导致铁芯被墩矮、墩粗等。

(a) (b)图2 磁路金相示图

本文要讨论的是，磁路铆接金相分析中的铁芯与轭铁铆接后存在的缝隙对电磁吸力的影响。文中，根据十字花铆、旋铆、锥铆等组装方式将铁芯与轭铁的配合间隙按不同形状和程度进行模拟仿真并对结论用样品进行实际验证。同时借此提出相适应的十字花铆的铆头设计尺寸要求。以减少产品在装配时反复的调整及金相分析验证。

根据金相分析的典型图片，我们在此提出磁路铆接的两个过程参数K1、K2：

铁芯接触面积比K1=铁芯与轭铁铆后贴合面积S1/(铁芯周长C×轭铁厚度T)

铁芯受力面积比K2=铁芯被铆压面积S2/铁芯截面积S

其中，K1将铆接缝隙量化为铁芯与轭铁接触面积的百分比，做为电磁吸力仿真的参数。K2量化的是铁芯受力变形的影响程度，以金相分析、铆接强度等进行验证。

2 仿真分析

2.1 仿真模型

仿真分析的模型，我们选择典型的拍合式继电器的简化磁路建立去参数的ANSYS仿真模型[1]，如图3所示。设定铁芯尾部为圆柱形，铁芯尾部与轭铁孔的配合间隙设为零件尺寸公差0.1mm。

图3中，0#模型的K1=100%，轭铁厚度T=1.0mm。磁路落差0.05mm。

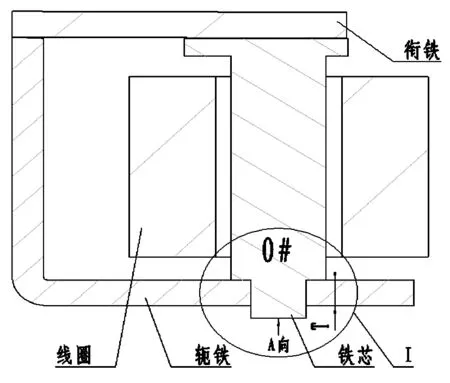
图3 简化模型图示

2.2 仿真分析对象

通过调整铁芯铆接位置尺寸，将K1量化为80%、65%、50%、35%、20%，见表1。并根据不同的装配气隙将仿真模型分3组。

1) A组为旋铆、锥铆等产生的环形配合间隙，且铁芯台阶面与轭铁的轴向间隙为δ=0。受铆接力影响，铁芯台阶根部的位置存在不同程度的配合间隙。

A组中，铁芯接触面积比K1=(铁芯周长C×铁芯与轭铁贴合高度t)/(铁芯周长C×轭铁厚度T)=t/T。见图4。

2) B组即为本文所提出的十字花铆方案形成的配合间隙，见图5。铁芯台阶面与轭铁的轴向间隙为δ=0。

铁芯接触面积比K1=(铁芯被铆压弧长C1×厚度T)/(铁芯周长C×厚度T)=(c1-1×4)/C

3) C组分为在K1=50%的情况下，铁芯台阶面在铆接区域存在轴向上0.1mm的配合间隙C1组，见图6。以及铁芯台阶面与轭铁面存在轴向间隙δ的C2组，示意见图7。

将各仿真模型的按K1参数对比，见表1：

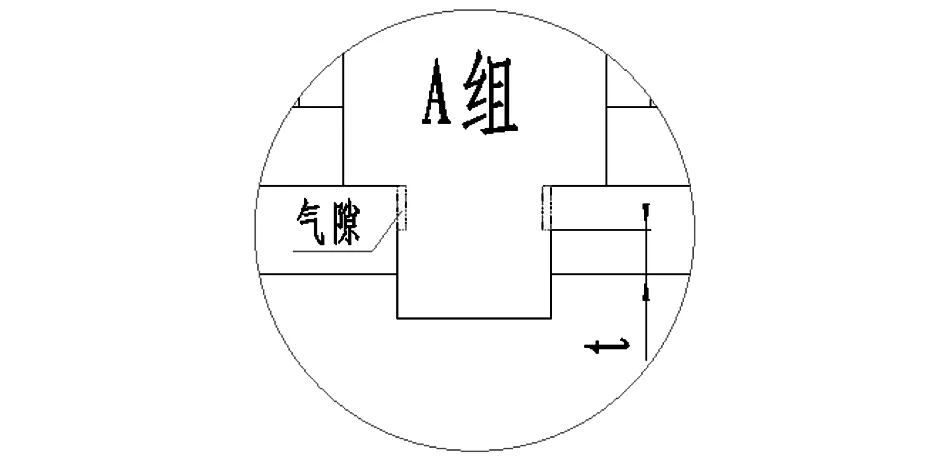
图4 A组模型局部放大图

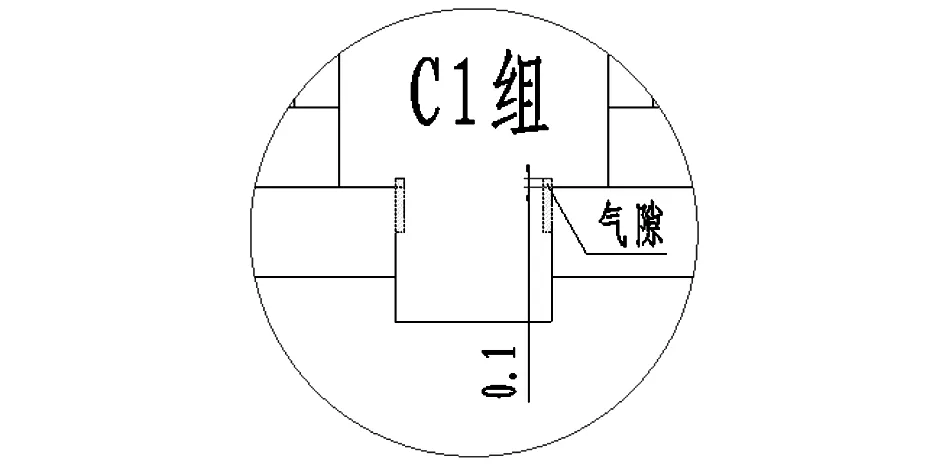
图6 C1组模型局部放大图

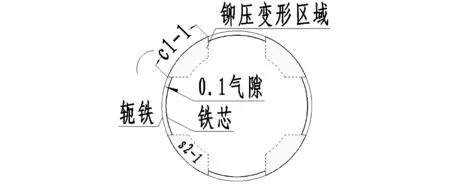
图5 B组模型铁芯横截面(图3 A向视图)

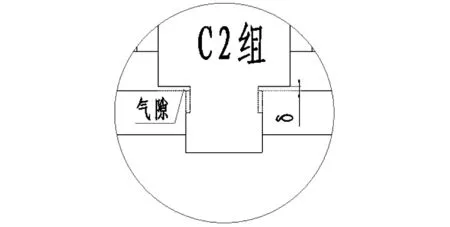
图7 C2组模型局部放大图

接触面积比K1模型编号A组B组接触面积比K1模型编号C组备注80%1#11#65%2#12#50%3#13#35%4#14#20%5#———50%C121#十字花铆22#锥铆C223#δ=0.02mm24#δ=0.05mm25#δ=0.10mm

将各模型导入Ansoft仿真分析软件，根据各零件材料赋予相应的材料属性，如轭铁、铁芯、衔铁均为电工纯铁DT4E；线圈绕组选择铜copper。在给线圈额定安匝以及70%额定安匝激励条件下分别计算衔铁从闭合位置(0°)至释放位置(2.5°)的过程中受到的吸力矩以及磁感应强度B的分布云图。

2.3 仿真分析结果

通过仿真分析可计算得到各模型的吸力值。排序图见图8、图9。

从图中可以看出，铁芯接触面积比K1≥20%，不论是十字花铆间隙还是环形间隙，其吸力曲线与0#模型吸力曲线基本重合，达到0#模型吸力的99.2%以上。铆接区域范围内的轴向间隙可以接受。但铁芯台阶面存在轴向间隙δ时，其吸力下降明显，见23#、24#、25#曲线，δ越大，吸力下降越明显。

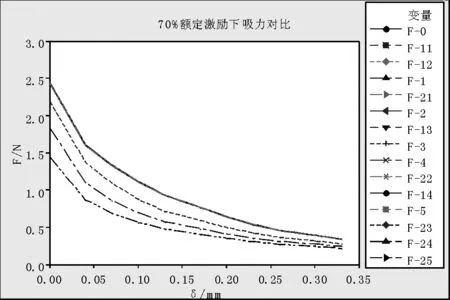
图8 70%额定安匝激励下吸力对比

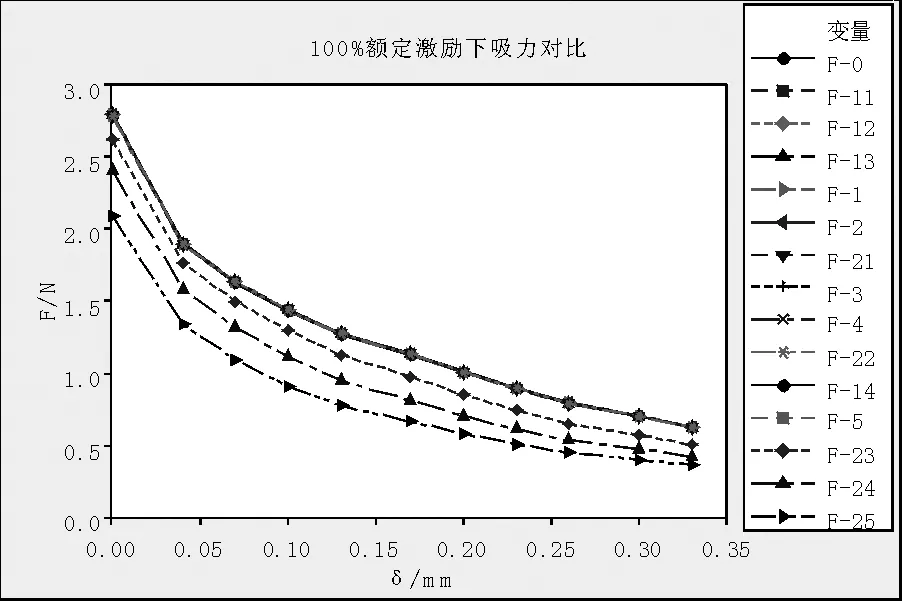
图9 额定安匝激励下吸力对比

3 仿真分析验证

根据分析结果，我们进行样品装配。其中，K1值采用金相切片方式确认。

3.1 吸力值验证

吸力值测试采用我司自制的吸反力测试装置[2]。得到的吸力实测曲线与仿真曲线见图10、图11。

图10 70%IN激励下仿真值与实测值对比

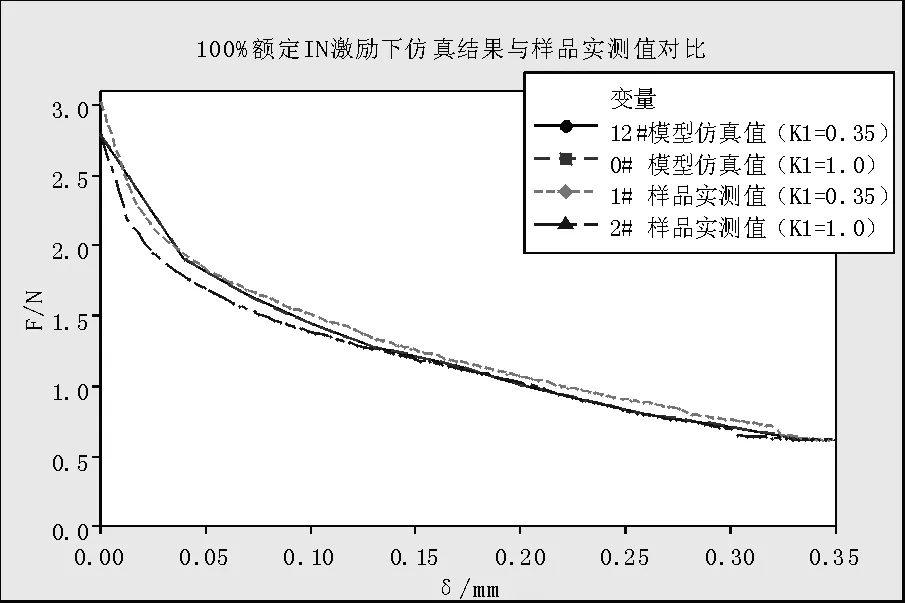
图11 额定IN激励下仿真值与实测值对比

仿真结果与实测曲线存在的差异与工程参数相关，我们认为仿真结果与实测值基本吻合。

综上，可以认为当铁芯接触面积比K1≥20%，吸力变化不显著，过程中可以接受。

3.2 铆接质量验证

从图5中，我们可以通过计算得到B组十字花铆的K2值：

铁芯受力面积比K2=铁芯被铆压面积S2/铁芯截面积S=(s2-1×4)/S。

从大量的金相分析及铆接强度测试结果来看，K2值太大，例如，K2≥40%时，铁芯台阶面的轴向间隙δ无法控制，将导致产品吸力下降，影响产品性能。同样，K2值太小，例如，K2<10%时则存在铆迹不清晰，无法量化测量且铆接强度不足等问题。

本文认为，在K2值适当的情况下，可以令铁芯局部受压变形，在该区域内易于达到铁芯100%贴平并涨紧轭铁的效果。而在铁芯未受力区域则为零件公差产生的配合间隙，即，K1值可控。

通过前面的仿真分析及样品验证，我们得到K1≥20%的结论，而受到工件强度等的影响，我们一般选择K1≥35%；此时K2≥10%。

下面，通过不同规格铁芯的金相分析及实际强度测试等评价来选择合适的K2值。因各规格铁芯的铆接强度等要求差异，本文对铆接质量及金相分析结果采用5分制进行评分，见表2。

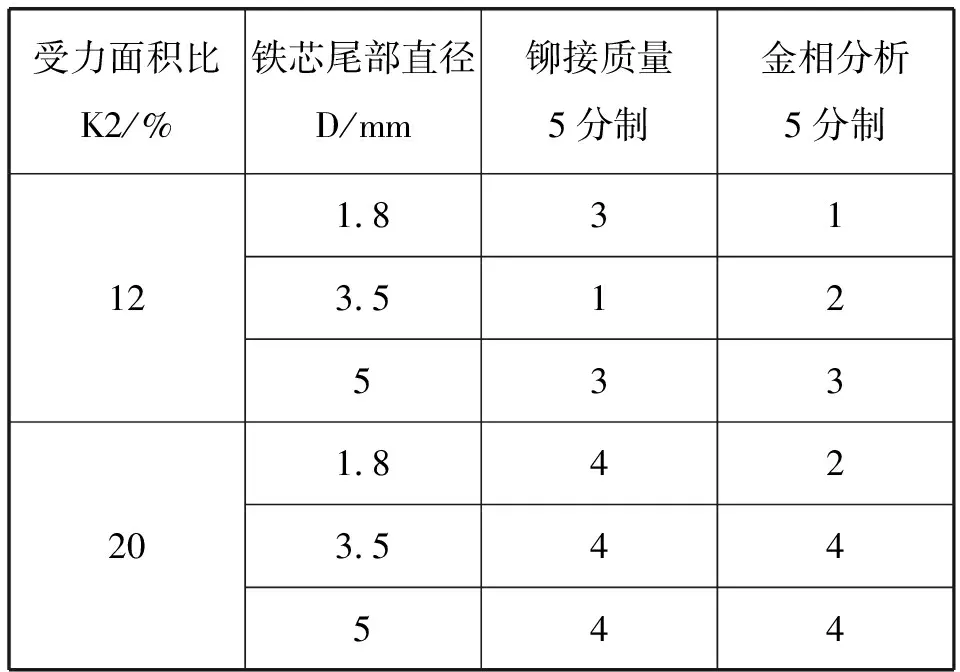
表2 K2值与铆接质量评价表

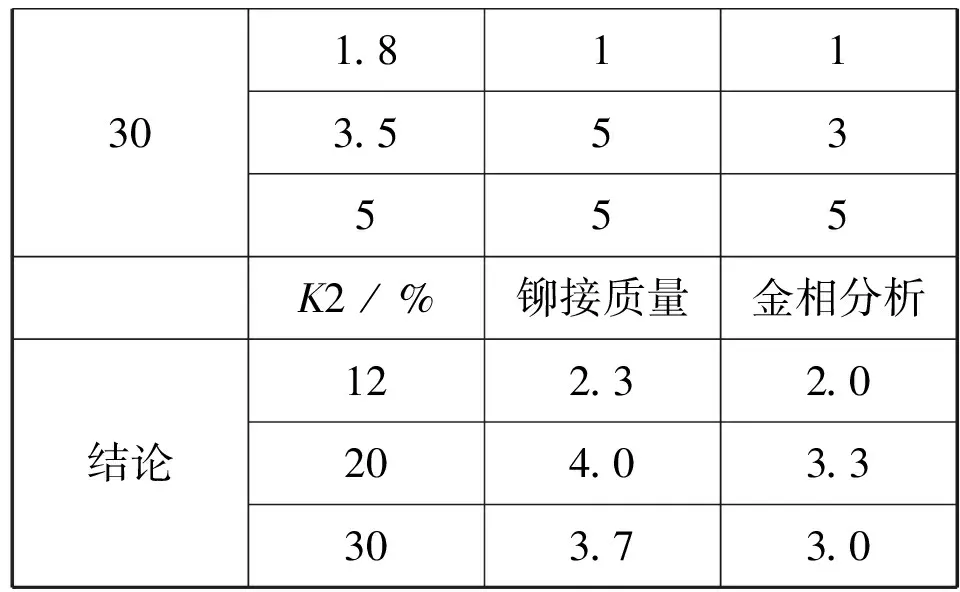
301.8113.553555K2 / %铆接质量金相分析结论122.32.0 204.0 3.3 303.7 3.0

从表2的评价结果看，K2值在20%时评价最好，铁芯尾部直径大于Φ3.5时，K2值可以放宽至30%。综合考虑，K2在20%～30%区间选择较恰当。

4 结束语

以典型的拍合式直流电磁继电器产品为模型进行磁路吸力矩仿真分析的结果是：在接触面积比K1≥20%，铁芯轭铁配合间隙≤0.1mm的情况下，十字花铆或锥铆、旋铆等铆接方案对磁路吸力无显著影响，铆接区域范围内铁芯台阶位置的轴向间隙对吸力影响不显著，需要完全杜绝的是铁芯台阶面与轭铁完全不贴平的轴向间隙δ。

从验证效果上看，十字花铆方案可通过铁芯受力面积比K2的调整，保证铆接区域铁芯与轭铁贴紧无缝隙，令铆接金相分析、铆接强度等达到标准要求。

采用十字花铆时，可以将铆头尺寸设计为令铁芯接触面积比K1≥35%，受力面积比K2=20%～30%，铆头的直径达到110%铁芯尾部直径，铆花的深度可设定为当工装闭模时与轭铁下表面贴平。

以上的结论将在今后的工作中进一步确认及优化。