高海拔隧道出碴车排放一氧化碳的扩散规律

孙三祥，王 文，郭慧杰，雷鹏帅,2，张 健,3

(1.兰州交通大学 环境与市政工程学院，甘肃 兰州 730070；2.兰州交通大学 寒旱地区水资源综合利用教育部工程研究中心，甘肃 兰州 730070；3.兰州交通大学 甘肃省轨道交通力学应用工程实验室，甘肃 兰州 730070)

现场实测结果表明，高海拔隧道钻爆法施工过程中，出碴阶段CO排放量及浓度最高[1-2]。王耀等[1]采用CO检测仪，测试分析了川藏公路雀儿山隧道(海拔4 000 m)爆破作业、内燃机械的CO排放量以及隧道内CO浓度变化趋势，得出在出碴阶段内燃机械累计排放的CO总量多于爆破阶段，施工机械，尤其是出蹅车排放的CO在出碴阶段对隧道内环境造成了严重污染。张玉伟等[2]采用便携式CO检测仪，跟踪监测了康定瓦九(瓦泽至九龙)公路鸡丑山隧道(海拔4200m)不同施工阶段CO浓度，得出在出碴阶段工作区CO浓度最高。

国内外专家对隧道施工期的通风进行了研究[3-5]，并对平原地区隧道爆破后CO的扩散进行了模拟研究。邓祥辉等[6]采用RNGκ-ε湍流模型，基于ADINA软件中的CFD模块，对隧道内爆破后的CO扩散规律以及工作人员进洞安全时间进行了数值模拟；李孜军等[7]采用RNGκ-ε湍流模型，基于Fluent软件模拟分析了双洞隧道独头掘进爆破作业后CO扩散规律；王晓玲等[8]采用高雷诺数κ-ε数学模型，基于STAR-CD软件，模拟分析了爆破后不同通风时刻隧洞内CO迁移和分布规律。但高海拔地区，由于气压、空气密度和含氧量均较低，内燃机燃烧不充分，因此CO扩散规律有别于平原地区。

针对高海拔隧道爆破后CO浓度扩散的模拟，曹正卯等[9]依托新关角隧道(海拔3 300 m以上)，采用κ-ε湍流非稳态模型，基于Fluent软件，模拟分析不同海拔高度施工爆破后有害气体浓度分布，得出了同一测点有害气体质量浓度与海拔高度的关系式，但未考虑施工机械及出蹅车的影响。

针对隧道出碴阶段CO浓度扩散的模拟，刘敦文等[10]采用RNGκ-ε湍流模型，基于Fluent软件，应用组分传输模型，得出了平原地区隧道出碴过程CO浓度场，提出了CO浓度限值及安全连续作业时间。专家还就隧道施工过程中车辆对隧道速度场及通风效果的影响，且大多采用二维动网格模型模拟[11-12]，而对高海拔隧道出碴车运行过程中排放CO浓度扩散的模拟目前未见报道。

因此，本文选取RNGκ-ε湍流模型，利用动网格及用户自定义函数，选用弹簧近似光滑模型、局部重划模型计算网格的动态变化；考虑海拔对气压和空气密度的修正；由通用有限速率模型反映CO与空气的耦合；仅考虑出碴车排放的CO，其他机械排放的CO作为固定源；基于Fluent软件，进行通风工况下出碴车运行过程中高海拔隧道内气流速度场和压力场、CO浓度场的三维非稳态数值模拟。基于出碴过程现场实测数据验证模拟结果。根据模拟结果分析出碴车排放CO扩散规律及行驶间隔时间，为高海拔隧道施工通风方案的制订提供一定的理论支持。

1 模型建立

1.1 隧道三维模型

以在建的采用钻爆法施工的敦格铁路当金山单洞单线特长隧道(平均海拔3 000 m)为例建立隧道三维有限元模型和网格简图，取正洞长度为1 600 m，平导长度为2 000 m，动网格计算长度为100 m。隧道洞身坡度为12.3‰，单面上坡。出碴车简化为长×宽×高为8.55 m×2.49 m×3.45 m的六面体，底面距地面高0.6 m，出碴车尾气管口位于车体左壁，距车头3 m，距地面0.8 m，出口直径为0.08 m。隧道风筒直径为1.2 m，位于隧道侧壁中上部，正洞风筒距掌子面30 m，压入式通风。采用非结构化四面体网格对流场区域进行网格划分，对出碴车车体周围及车头、车位部网格进行加密，如图1所示。通过网格敏感性分析，确定最终节点数62 905个，网格数337 448个。出碴车行驶及CO排放对应流场采用动网格划分。

1.2 动网格模型的建立

将隧道内气流场分为出碴车运动区域和不运动区域，基于Fluent软件提供的DEFINE_CG_MOTION和DEFINE_PROFILE宏，应用C语言编译用户自定义函数，建立出蹅车运动和CO排放速度变化的动网格模型。

1.3 气流流动与CO扩散的方程

1.3.1 基本假设

(1)通风气流为不可压缩流体。

(2)气体在稀释扩散过程中不发生化学反应及相变反应。

(3)隧道壁面为等温壁面。

(4)仅考虑出碴车排放CO的扩散，将其他机械排放的CO统一作为固定源，即将出蹅车通过监测点前的CO浓度值作为模拟计算中的背景值。

1.3.2 基本方程

选取RNGκ-ε湍流模型，建立气流流动与CO扩散的方程，包括基本控制方程(质量守恒方程、动量方程、能量方程)、湍动能方程、湍动能耗散率方程和组分输运方程，分别如下。

(1)基本控制方程通式为

(1)

式中：t为时间，s；ρ为流体密度，kg·m-3；φ为待求通用物理量；U为速度矢量；Γφ和Sφ分别为对应变量的广义扩散系数和广义源项。

(2)湍动能κ方程为

(2)

其中

式中：ui和uj为速度分量，m·s-1；κ为紊流动能，m2·s-2；xi和xj为坐标；μt为紊流动力黏性系数，Pa·s；σκ为湍流普朗特数，σκ=1.00；ε为紊流的动能耗散率，m2·s-3；μeff为有效黏性系数；μ为层流动力黏性系数，Pa·s；cμ为经验常数，取值0.09；G为紊流脉动动能产生项。

(3)湍动能耗散率ε方程为

(3)

式中：σε，c1，c2均为经验常数，σε=1.30，c1=1.44，c2=1.92。

(4)组分输运方程为

(4)

1.3.3 边界条件

(1)进口边界：出碴车排气管为CO进口边界。基于现场测试结果，确定尾气管出口CO浓度最大值为427 mg·m-3，对应尾气温度为600 K，尾气设置为空气与CO的混合体，其中CO在尾气中的质量百分比取0.042 7%。出碴车加速、匀速运行阶段CO的排放速度分别为30和23 m·s-1。现场实测隧道内风速为0.3 m·s-1，该风速设为隧道模型入口的风速。

(2)出口边界: 设为自由出流边界条件。

(3)壁面边界: 出碴车及隧道壁面设为壁面边界，出蹅车为滑移壁面，隧道壁面为无滑移绝热边界。

(4)正洞工作面需风量为1 000 m3·min-1，对应正洞风管出口风速为14.8 m·s-1，入口输送新鲜空气(即CO质量分数为0),空气温度为293 K。

2 数值模拟算法及算法验证

2.1 数值模拟算法

采用非定常隐式解法求解上述方程。其中速度迭代采用PISO算法；压力采用标准离散方式；其他参数的离散采用二阶迎风格式。网格的动态变化过程选用弹簧近似光滑模型和局部重划模型模拟。时间步长设置为0.01 s。

2.2 算法验证

采用现场实测数据对模拟结果进行验证。现场实测期间，隧道内气温为13.8～18.5 ℃，大气压为70.7～71.5 kPa。出碴车为陕汽德隆F3000型自卸车，自4号横通道运行到3号横通道。分别在距栈桥50，100，150 m的断面布置测点，并分别标记为测点1、测点2、测点3。测点位于出碴车右侧，且距右侧隧道壁面1.2 m，距隧道底面1.5 m。使用CD4(B)型多参数气体测定器检测CO浓度，数据采集时间间隔为15 s，持续监测300 s。

测点1不同时间间隔CO浓度的测定值与数值模拟值最大差值为0.12 mg·m-3，相对误差小于5%，可见两者吻合很好，由此表明，本文提出的模拟算法可以有效地揭示出碴车行驶过程中排放CO扩散规律。

3 数值模拟结果

3.1 出碴车运行速度曲线

根据现场监测，出碴车运行速度曲线取3种，如图2所示，即出碴车的加速时间均取4 s, 加速度a取1.00，1.25，1.50 m·s-2，对应的匀速运行速度v取4，5，6 m·s-1。

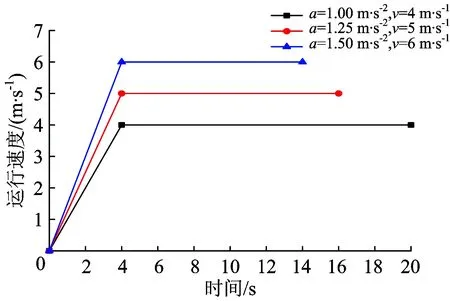
图2 出碴车运行速度曲线

3.2 出碴车环隙流特性

出渣车分别以图2中的3条速度曲线行驶至8 s时，车头环隙流速度分布如图3所示。其中，以加速度为1.50 m·s-2，对应速度为6 m·s-1的速度曲线行驶至8 s时，出碴车不同部位环隙流速度分布如图4所示。图中纵坐标环隙速度方向与车体同向为正，反向为负；横坐标以车体轴线为基准，运行方向右侧至隧道壁面的距离为正，左侧为负。由图3和图4可知：出碴车行驶速度越大，环隙流速度越大；出碴车行驶速度一定时，越靠近出碴车尾部，环隙流速度越大。

图3 出碴车以3种速度曲线行驶时环隙流速度分布

图4 出碴车不同部位环隙流速度分布

3.3 出碴过程中隧道内气流的压力场和速度场

考虑出渣车基本沿隧道中线行驶，以距隧道底面1.5 m高度的隧道中线为例，区分相同车速不同时刻、相同时刻不同车速2种情况，根据模拟结果绘制不同时刻气流的压力和速度的沿程(沿隧道纵向距离)分布图。

1)相同车速，不同时刻

以图2中出碴车的加速度1.50 m·s-2，匀速运行速度6 m·s-1的速度曲线为例，不同时刻气流的压力和速度的沿程分布曲线如图5和图6所示。

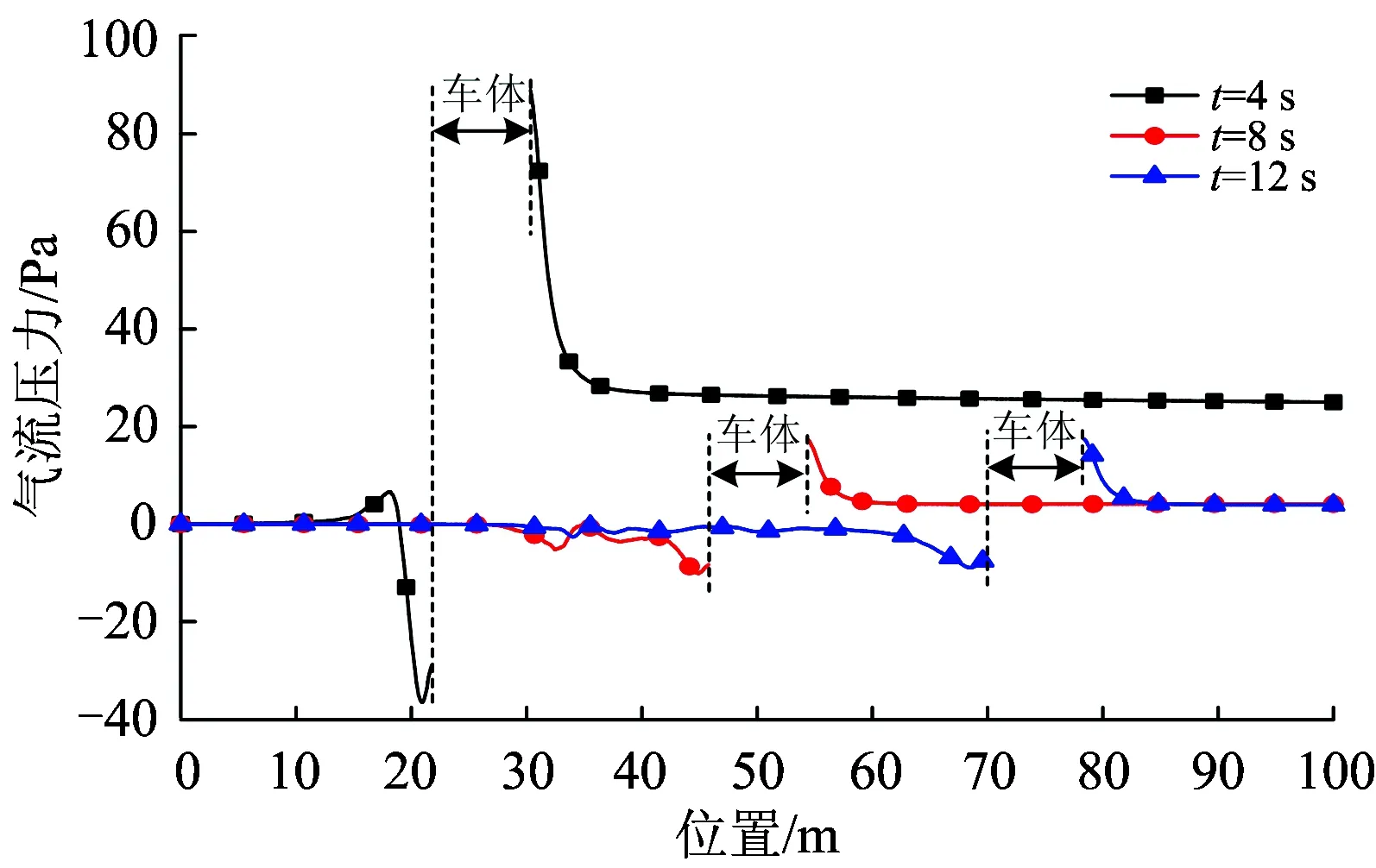
图5 不同时刻气流压力的沿程分布曲线

由图5可知：出碴车自启动(t=0)到加速结束时(t=4 s)，车头前端气流压力由0增大为90 Pa，车尾增大为36 Pa，车头为正压，车尾为负压，且气流压力均达到最大值；匀速行驶时，车头前端区间气流压力由0增大为18 Pa，车尾压力由0增大为10 Pa；加速结束时车头气流压力最大值是匀速行驶时最大值的5倍，车尾气流压力最大值是匀速行驶时最大值的3.6倍。

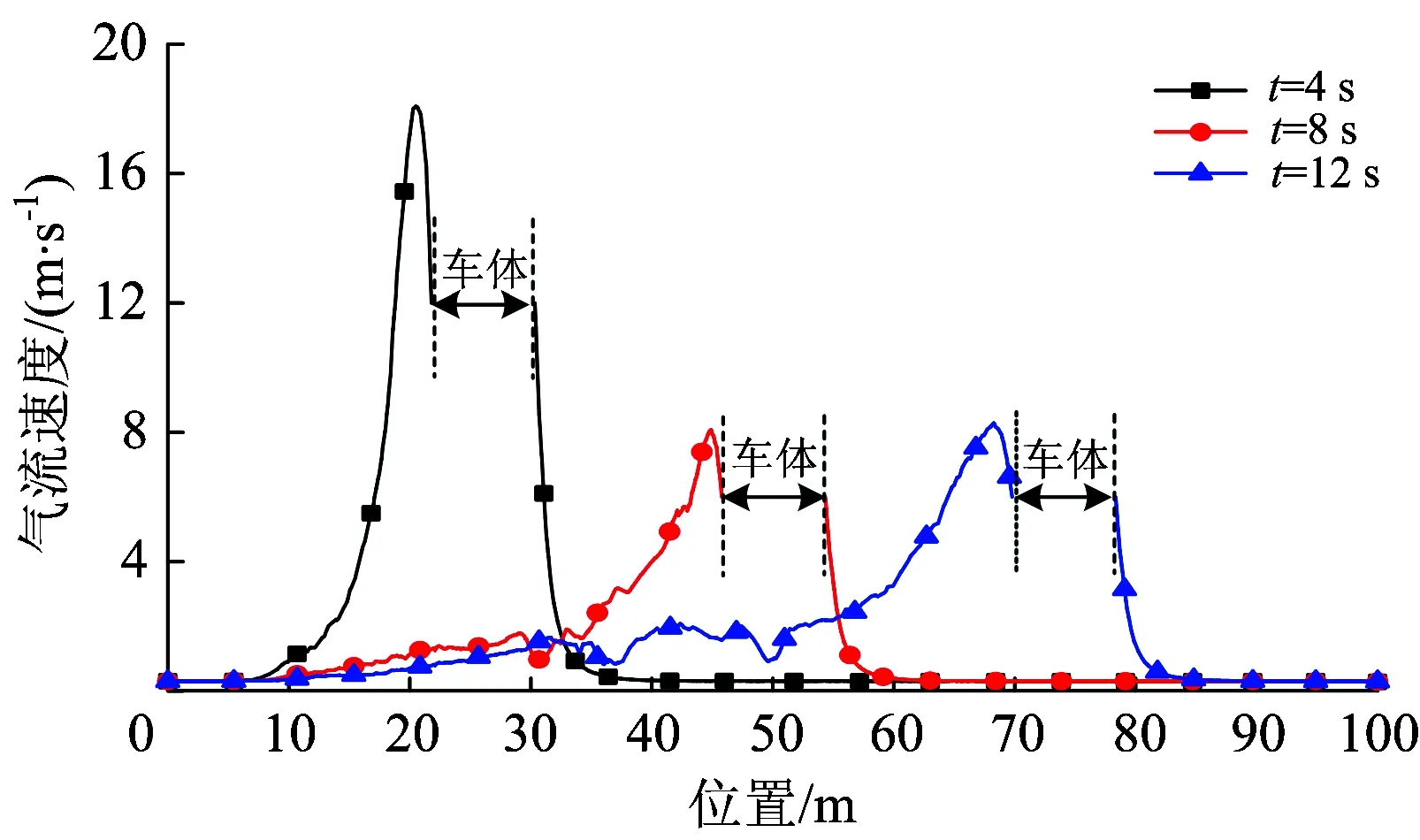
图6 不同时刻气流速度的沿程分布曲线

由图6可知：出碴车自启动(t=0)到加速结束时(t=4 s)，车体周围气流速度变化也最大，速度最大值出现在车尾；车头前端速度变化影响区域长度约5 m，车尾涡流区影响长度较大，且随时间的延续影响区域长度逐渐增大；出碴车加速阶段车体不同部位气流速度均远大于匀速行驶阶段，其中车尾涡流区速度最大，为匀速运行阶段车尾涡流区最大速度的2～3倍。

2)相同时刻，不同车速

以出碴车稳定运行12 s时刻为例，不同车速时气流压力和速度的沿程分布曲线如图7和图8所示。

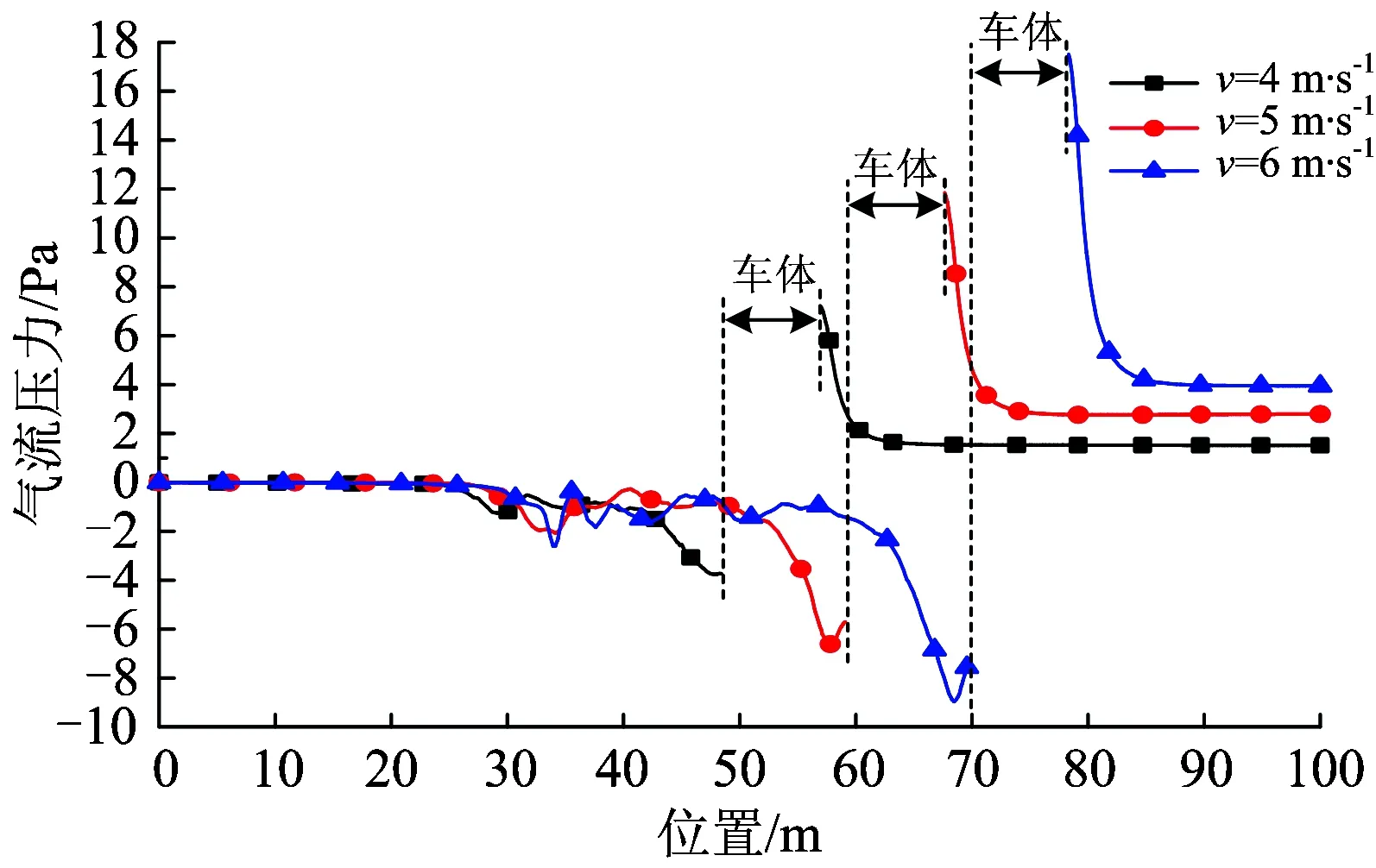
图7 不同车速时气流压力沿程分布曲线

图8 不同车速时气流速度沿程分布曲线

由图7可知：车头前端气流正压影响区域长度约5 m；远小于车尾负压区域长度；随着车速增大，车头前端压力及车尾负压均增大，即车头对前面空气的挤压、车尾对后部空气的抽吸越强，同时压力变化影响区域也增大；车头前端5 m以远区域压力沿程变化趋于稳定，不同车速形成的压差基本相同，约为1.2 Pa。

由图8可知：车头前端气流速度变化影响区域长度约5 m；车尾涡流区影响区域长度较大，且随时间的延续影响长度逐渐增大；车速越大，车尾涡流速度越大，影响区域长度越大；运行历时12 s后，3种车速下的气流速度场均趋于稳定。

3.4 出碴车行驶时CO浓度场

鉴于加速阶段历时短，重点分析出渣车匀速行驶阶段的CO浓度场。出渣车以图2中加速度1.50 m·s-2，匀速运行速度6 m·s-1的速度曲线行驶至8 s时，尾气管出口速度矢量图如图9所示。由图9可以看出：尾气管出口下方形成涡流区；受车速和环隙流的影响，出碴车尾部气流速度变大，紊动作用加强，从而增强了CO的扩散。

图9 尾气管出口速度矢量图

由于尾气管安装在车体左侧，车体行驶过程中尾气排放应属于浮射流范畴，其冲击浮射流基本特性与有限空间受横流影响的冲击射流有相似之处，二者间的区别另文讨论。

以图2中加速度1.50 m·s-2，匀速运行速度6 m·s-1的速度曲线为例，出渣车行驶至8 s时，距尾气管不同距离断面CO浓度分布云图如图10所示。由图10可知： CO主要集中在车尾涡流区；出碴车匀速行驶时，距尾气管出口越近，CO浓度越高，但超标(高于标准TB10204—2002《铁路隧道施工规范》中的限值30 mg·m-3)区域极小；单车匀速行驶时CO浓度超标，但超标区域的高度未达到人体呼吸高度。

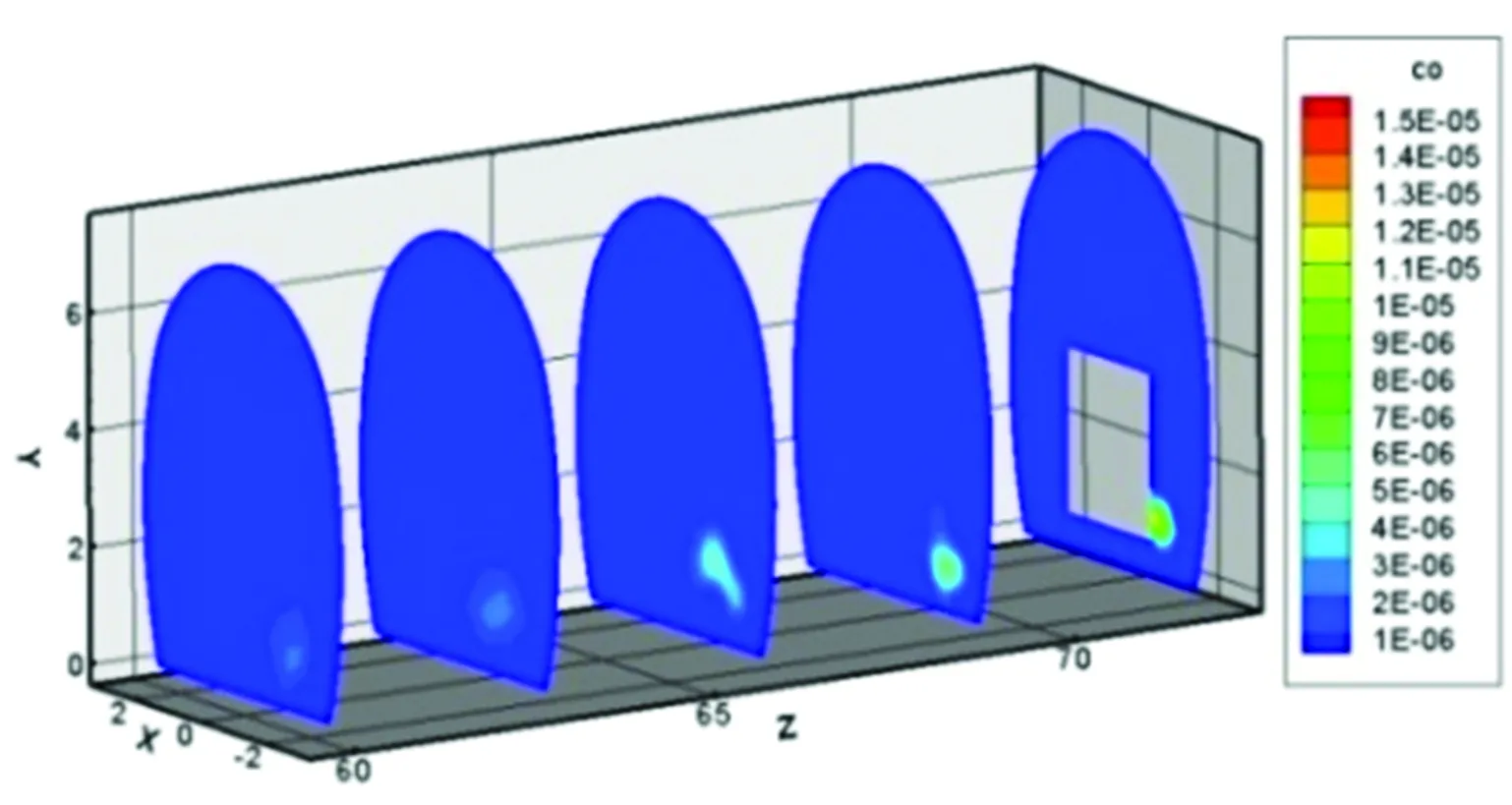
图10 距尾气管不同距离断面CO浓度分布云图

出渣车以图2中加速度1.50 m·s-2，匀速运行速度6 m·s-1的速度曲线行驶时，不同时刻、不同车速时隧道内CO浓度分布云图如图11所示。出渣车以图2中的3条速度曲线行驶至8 s时，CO浓度分布云图如图12所示。由图11和图12可得如下结论。

图11 不同时刻隧道内CO浓度分布云图

图12 不同车速时隧道内CO浓度分布云图

(1)CO自车体左侧的尾气管排出后，车体左侧尾部涡流区的CO浓度较高。

(2)出碴车行驶速度越大，尾部涡流影响区也越长，CO扩散作用越强。因此建议出碴车车速根据现场情况尽可能以较大车速匀速行驶。

(3)出碴车加速运行区段，CO累积严重，车体尾部浓度高，浓度超过标准限值30 mg·m-3。因此建议出碴车选择出碴路线时，尽量减少作业点，从而减少出碴车加减速的次数，以减少CO排放量；作业人员选择避让点时，应尽量选择在出碴车匀速行驶区段、远离车辆尾气管的一侧，避免选择在出碴车加速区段(例如在通过栈桥的区段)。

(4)出蹅车经过测点较长一段时间后，由于环隙流的作用，隧道顶部的高浓度CO向隧道底部运移，致使底部CO浓度升高。根据模拟结果，车速为4，5，6 m·s-1时，隧道内前、后2辆出碴车辆间隔时间大于5 min时，CO累积浓度不超过标准限值30 mg·m-3。因此，建议前、后2辆出碴车间隔时间尽量大于5 min。

3.5 出碴车尾部CO扩散规律

基于出碴车尾部CO浓度的分布云图，选取距车体中心线左侧1.2 m，距隧道底面1.5 m的点为观测点(该点断面浓度最大)，出渣车分别以图2中的3条速度曲线行驶至8 s时， CO浓度沿程变化曲线如图13所示。由图13可知，该曲线反映的扩散规律符合瞬时点源一维随流扩散方程基本解(不同车速拟合优度R2均大于0.8)，即按照e指数衰减。这也与文献[7]基于实测结果所得结论一致。

图13 CO浓度沿程变化曲线

隧道内污染物瞬时点源一维随流扩散方程基本解为[13]

(5)

式中：C为隧道内采样点空气污染物浓度，是时间t和位置x的函数，mg·m-3；C0为隧道内测点初始时刻空气污染物浓度，mg·m-3；u为隧道内气流速度，m·s-1；D为CO扩散系数，m2·s。

将式(5)进行变换可得

(6)

将图13对应的实测数据代入式(6)，可得出碴车不同车速时CO扩散系数沿程变化曲线，如图14所示。由图14可知：车速越大，车体尾部CO扩散系数越大；受尾部涡流的影响，距车尾近区，CO扩散系数较大，扩散较快，远离尾部涡流区，CO浓度扩散系数趋于稳定。

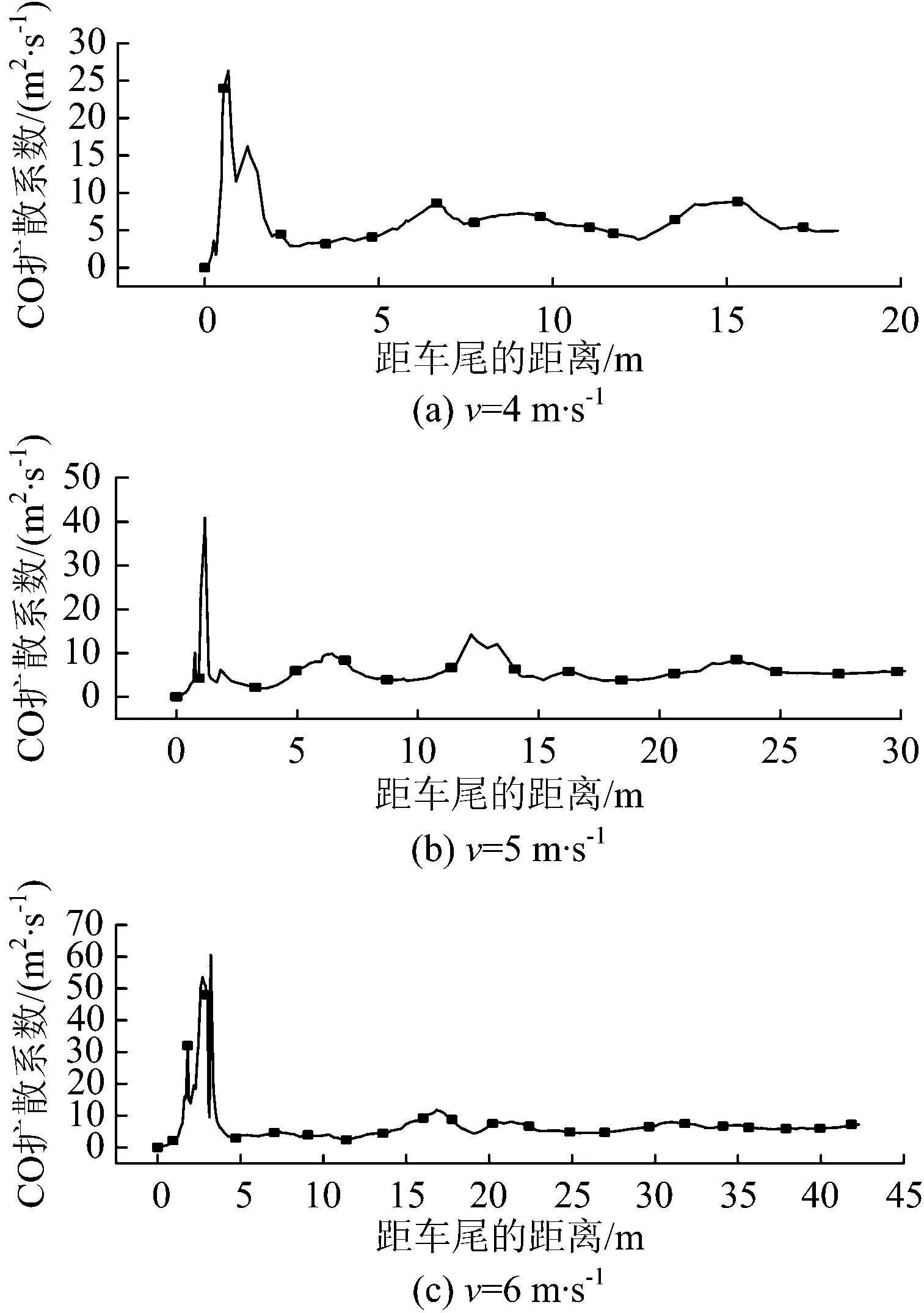
图14 CO扩散系数随距离的变化

为便于计算，考虑CO扩散系数与车速之间的关系，车速分别为4，5，6 m·s-1时对应的CO扩散系数均值分别为6.20，5.97，5.91 m2·s。

4 结 论

(1)出碴车分别以图2中3条速度曲线运行时，车头前端气流速度和压力变化影响的区域长度约为5 m，车尾影响的区域较长；出碴车运行速度越大，越靠近车辆尾部，环隙流速度越大；运行历时12 s后速度场均趋于稳定；加速阶段车体不同部位气流速度均远大于匀速行驶阶段，其中车尾涡流区气流速度最大，为匀速运行阶段车尾涡流区气流最大速度的2～3倍；随着车速增大，车头前端压力及车尾负压均增大，加速结束时，车头气流压力最大值是匀速行驶时最大值的5倍，车尾气流压力最大值是匀速行驶时最大值的3.6倍。

(2)CO主要集中在车尾涡流区；出碴车匀速行驶时，距尾气管出口越近，CO浓度越高，但超过标准限值30 mg·m-3的区域极小，且未达到人体呼吸高度；出碴车加速运行区段为CO高浓度积聚区，其浓度超过标准限值30 mg·m-3。因此建议：出碴车尽量减少作业点，并以较高的速度匀速行驶，以减少CO排放；作业人员选择避让点时，尽量选择在出碴车匀速行驶区段，且远离车辆尾气管的一侧。

(3)为了尽可能减小前后2辆出碴车行驶排放CO浓度的叠加，使CO累积浓度小于标准限值30 mg·m-3，建议前后2辆出碴车行驶间隔时间大于5 min。

(4)出碴车运行过程中，CO扩散规律符合瞬时点源一维扩散方程基本解，即按照e指数衰减。车速越大，车体尾部CO扩散系数越大；受尾部涡流的影响，距车尾近区，CO扩散系数较大，远离尾部涡流区，CO扩散系数趋于稳定。