近距离垂直交叠盾构隧道的列车振动响应特性及损伤规律
晏启祥,陈文宇,陈 行,唐启童,包 芮,黄 希
(1.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031;2.西南交通大学 土木工程学院,四川 成都 610031;3.中国中铁二院成都勘察设计研究院有限责任公司 桥隧设计处,四川 成都 610031)
随着高速铁路的快速发展,铁路隧道数量急剧增加,不可避免地会出现空间立体式的交叠隧道。这种交叠隧道结构的受力较为复杂,在上部和下部列车振动荷载的作用下,极易在关键部位出现应力集中现象,对隧道结构产生损伤和破坏[1-3]。因此,研究近距离空间交叠盾构隧道衬砌在列车振动荷载作用下的动力响应特性和损伤规律,对保障隧道在长期运营过程的安全性和稳定性具有重大意义。
目前,国内外关于铁路隧道结构在列车振动荷载作用下的动力响应特性已展开了研究,取得了一定的成果。高峰等[4]研究了深圳地铁重叠隧道在列车上行、列车下行和列车上下交会动载情况下的动力响应规律;黄娟[5]通过不同加载频率的动态模型试验研究了高速铁路隧道仰拱的动力特性;李亮等[6]分析了列车振动荷载作用下,大断面隧道支护结构在不同车速、阻尼比系数和断面形式下的动力响应特性;龚伦等[7]以上海轨道交通9号线盾构隧道下穿沪杭铁路干线为背景,采用三维动力有限元方法对列车动载引起下穿隧道的振动影响进行了研究;莫海鸿等[8]以广州地铁4号线盾构隧道为例,采用三维动力有限差分法,研究了深厚软土盾构隧道在地铁营运期间的动力响应特性;杨文波等[9]采用模型试验与数值模拟方法,研究了列车振动荷载全频域内隧道衬砌结构及周围软土地层的频率响应函数,分析了在不同频率荷载作用下衬砌结构的内力分布规律。这些研究大多数是针对隧道结构的动力瞬态响应,而对交叠隧道结构的损伤规律以及不同间距下隧道结构振动特性的研究较少。
因此,本文针对近距离垂直交叠盾构隧道结构的特性,采用ABAQUS有限元软件,基于结构的动力和损伤分析方法,建立列车振动荷载作用下近距离垂直交叠隧道数值模型,研究列车振动荷载作用下近距离垂直交叠盾构隧道衬砌的动力响应特性及不同净间距情况下垂直交叠隧道的损伤规律。
1 垂直交叠盾构隧道结构数值模型
目前,国内外逐步出现了一些高速铁路盾构隧道[10-11],且随着我国隧道交通网络的快速发展,将会出现垂直交叠的盾构隧道。本文以探索性的方式对垂直交叠盾构隧道进行研究。该垂直交叠隧道处于Ⅴ级风化岩中,2个隧道的横断面相同,净距为6 m。设计列车时速为350 km·h-1。采用ABAQUS软件对垂直交叠盾构隧道建立三维有限元模型。2个隧道均以垂直交叠的中间横断面为左右对称,上部隧道纵向长度取1 200 m,拱顶距地表38 m,下部隧道纵向长度取1 000 m。衬砌混凝土等级为C50,抗渗等级为S15。隧道内径为9.8 m,外径为10.8 m,幅宽为1.5 m。管片采用通用环进行拼装,分块方式为“5+2+1”,如图1所示。为便于计算,仅考虑上部隧道中间位置的5环管片和下部隧道中间位置的3环管片,对其余位置的管片进行简化,即对管片进行刚度折减,从而模拟纵向接头的影响,刚度折减系数取0.8。近距离交叠盾构隧道三维数值模型如图2所示。
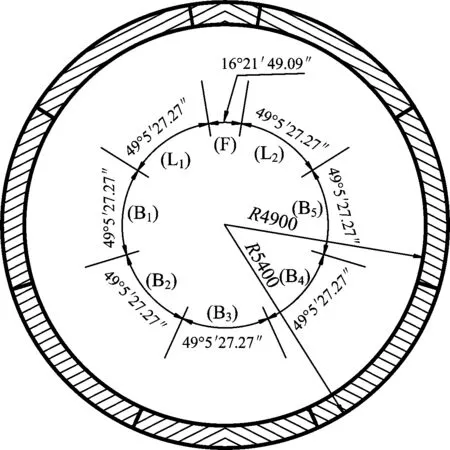
图1 隧道衬砌管片结构(单位:mm)

图2 近距离垂直交叠盾构隧道三维数值模型
岩土体采用摩尔库伦本构关系,隧道衬砌采用基于连续介质的混凝土塑性损伤本构模型(CDP模型)[12]。振动系统阻尼采用瑞利阻尼[13],阻尼比ξ0取0.05。为最大程度吸收振动波在模型中的相互影响作用,模型的边界采用黏弹性人工边界。地层采用深厚均匀地层。岩土体及结构的参数取值见表1。
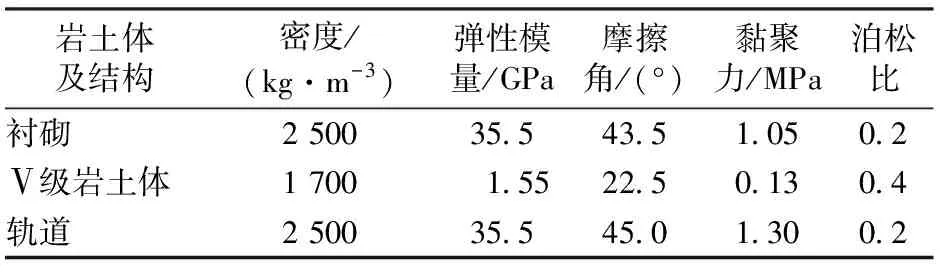
表1 岩土体及结构的物理力学参数
2 列车振动荷载
高速列车的时速为350 km·h-1,6辆编组,长度L=150 m,轴重为17 t,弹簧下质量M0=750 kg。由我国高速铁路的运行标准,给出了对应3种控制条件下不平顺振动的波长L和矢高h,分别为L1=10.0 m,h1=3.5 mm;L2=2.0 m,h2=0.4 mm,L3=0.5 m,h3=0.08 mm。上部隧道纵向长度为1 200 m,则列车通过隧道所用时间为(1 200+150)/(350×1 000/3 600)=14 s。采用国际通行的荷载时程拟合公式[14],得到高速列车在隧道内的振动荷载F1(t)如图3所示。

图3 列车振动荷载时程曲线
3 垂直交叠盾构隧道振动响应特性及损伤分布规律
高速列车在上部隧道行驶,分析在该列车振动荷载作用下近距离垂直交叠盾构隧道的动力响应特性和损伤分布规律。
3.1 隧道衬砌振动加速度时程分析
选取上部隧道中间位置的横断面为分析断面S。分析断面S上拱顶、拱腰和拱底处衬砌的振动加速度时程曲线如图4所示。
从图4可知:列车距离分析断面越近,分析断面上隧道衬砌的振动加速度响应越大;约在6.9 s时,即列车中部到达监测断面S时,衬砌的振动加速度响应最为剧烈,振动加速度达到峰值,其中拱底处的振动加速度峰值最大,约为1.72 cm·s-2;拱腰处的次之,约为1.12 cm·s-2;拱顶处的最小,约为0.58 cm·s-2;可见拱底处衬砌的振动加速度峰值分别约为拱腰、拱顶处的1.54倍和2.97倍。
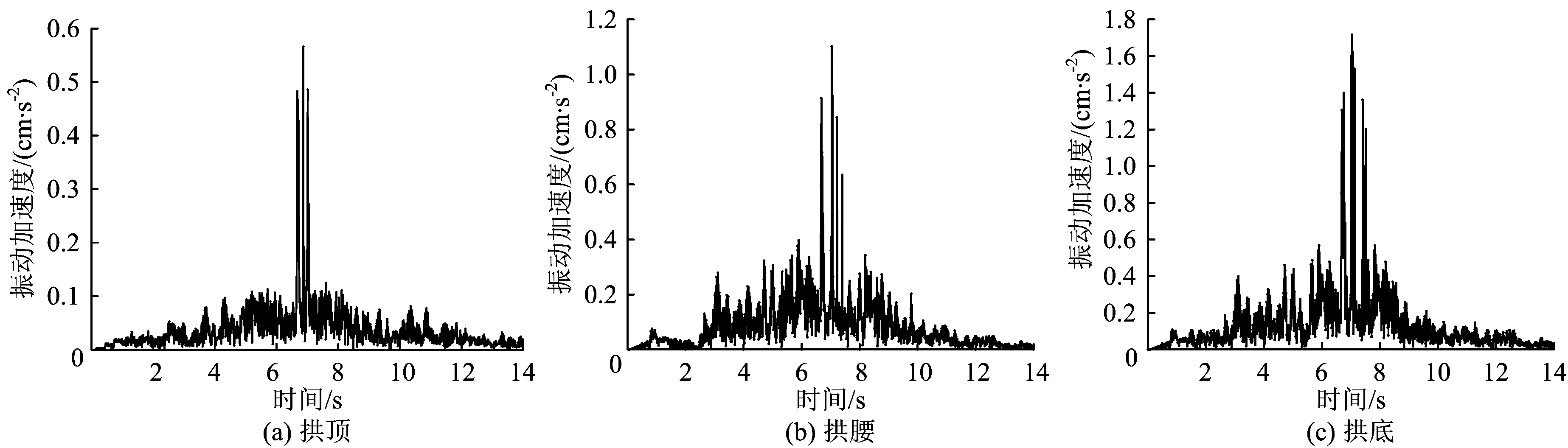
图4 上部隧道分析断面S上拱顶、拱腰和拱底处衬砌的振动加速度时程曲线
3.2 隧道衬砌最大主应力增量时程分析
在上部隧道的拱底设置分析点A1,A2,A3,其中A2点位于分析断面S上,A1和A3均距离A2点300 m;在下部隧道的拱顶设置分析点B1,B2,B3,其中B2点位于下部隧道中间位置的横断面X上,B1和B3均距离B2点250 m;如图5所示。提取各分析点的最大主应力增量(即分析点在列车振动荷载作用下的最大主应力相对于静态下最大主应力的增量)进行分析。上部隧道衬砌各分析点的最大主应力增量时程曲线如图6所示。
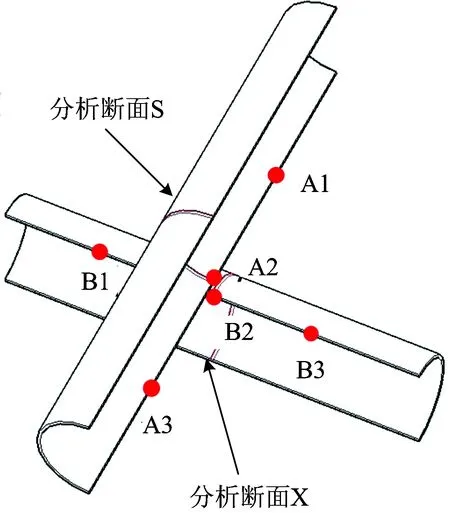
图5 交叠隧道衬砌各分析点布置图
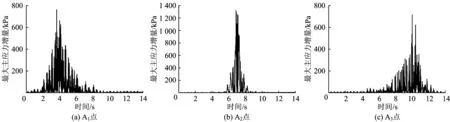
图6 上部隧道衬砌各分析点最大主应力增量时程曲线
由图6可知:列车距离分析点越近,分析点处振动最大主应力增量响应越大;在2~9 s间,列车距离A1点较近,A1点出现较为剧烈的振动,其中约在3.9 s时,列车中部到达A1点,A1点最大主应力增量达到峰值,为780 kPa;在5.8~8.3 s间,列车距离A2点较近,A2点出现明显的剧烈振动,其中约在6.9 s时,列车中部到达A2点,A2点最大主应力增量达到峰值,为1 300 kPa;在6~13 s间,列车距离A3点较近,A3点出现剧烈的振动,其中约在10 s时,列车中部到达A3点,A3点最大主应力增量达到峰值,为720 kPa。
对比3个分析点的最大主应力增量峰值可知,A2点的最大,分别约为A1点、A3点的1.67倍和1.81倍,说明由于下部隧道的影响,上部隧道在交叠处的最大主应力增量出现放大效应。
下部隧道衬砌各分析点最大主应力增量时程曲线如图7所示。从图7可知:列车距离分析点越近,分析点的振动最大主应力增量响应越大;在4~11 s间,下部隧道各分析点的最大主应力增量较大,且B2点远大于B1和B3点,约在6.9 s时,B1,B2,B3分析点的最大主应力增量均到达峰值,分别为26,130和24 kPa,且B2点的分别约为B1点、B3点的5.00倍和5.42倍。
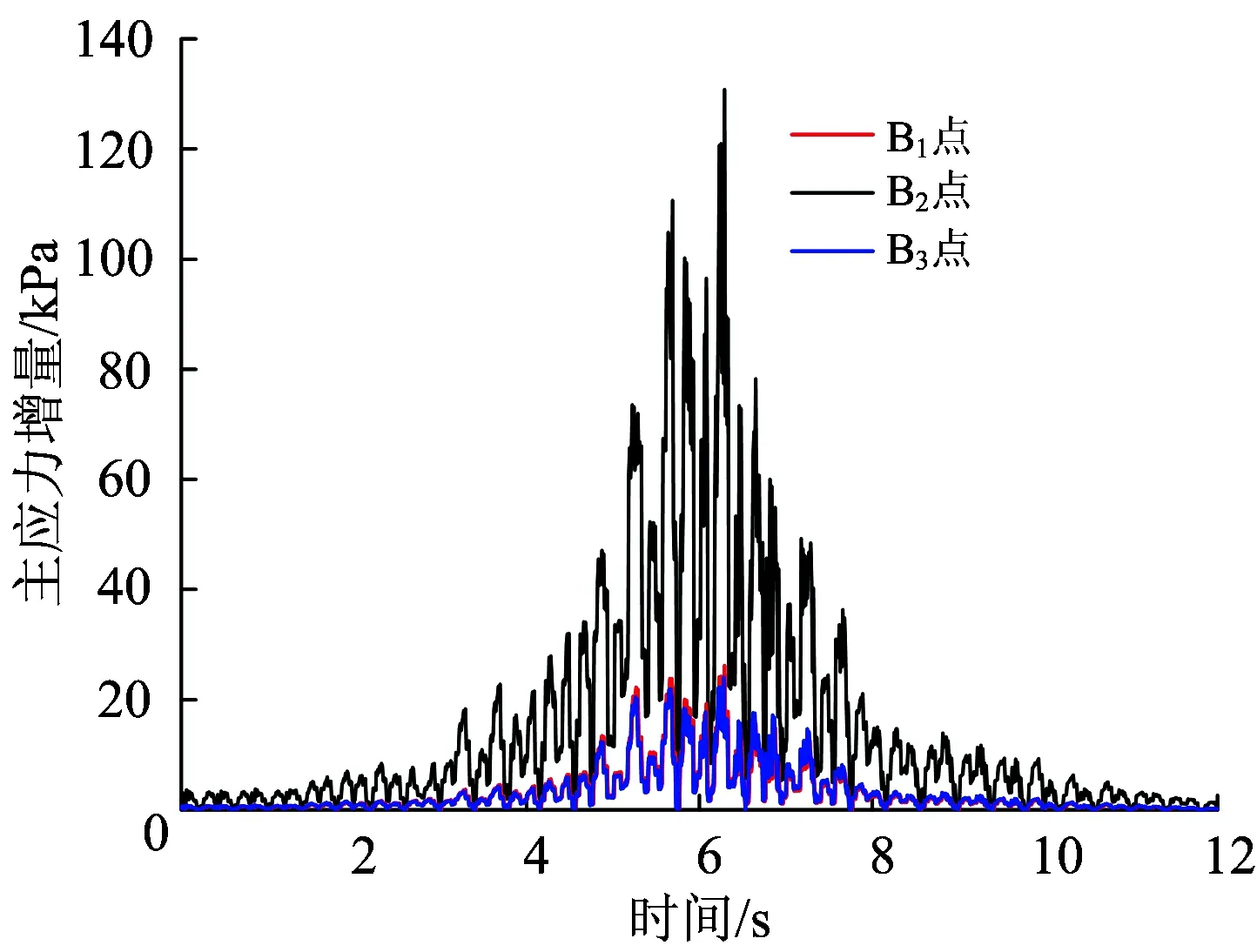
图7 下部隧道衬砌各分析点最大主应力增量时程曲线
对比上下部隧道衬砌各分析点的最大主应力增量可知:上部隧道3个分析点的最大主应力增量的峰值均大于下部隧道的,其中A2点的振动响应远大于B2点的,A2点的最大主应力增量峰值(1 600 kPa)为B2点的(130 kPa)的12.31倍。
3.3 不同间距时上部隧道衬砌损伤
由以上分析可知,上部隧道受到列车振动所产生的损伤要大于下部隧道,故选择上部隧道进行不同间距下的损伤规律分析。在上部隧道分析断面S的前后300 m再各设置1个监测断面S1和S2,并在各断面上选取23个单元,如图8所示。设置上下两隧道的净距分别为2,4,6 m。提取垂直交叠隧道上部隧道各断面上各单元在不同净距下的损伤值,得到各断面的压致和拉致损伤沿衬砌环的分布情况,如图9和图10所示。
从图9可得如下结论。
(1)在同一断面上,沿环向的压致损伤区主要分布在上部隧道底部约130°的范围内,而拱顶附近不太显著。压致损伤分布呈现如下特征:拱底最大,两侧拱腰次之,其余位置较小。
(2) 交叠隧道在交叠中心处断面S的压致损伤最大,并且比断面S1和断面S2均明显增大。在上下隧道净距为2 m时,断面S的拱底压致损伤峰值为断面S1和断面S2的6.71倍和6.62倍。这是由于受到下部隧道的影响,说明交叠隧道的压致损伤在交叠处具有放大效应。
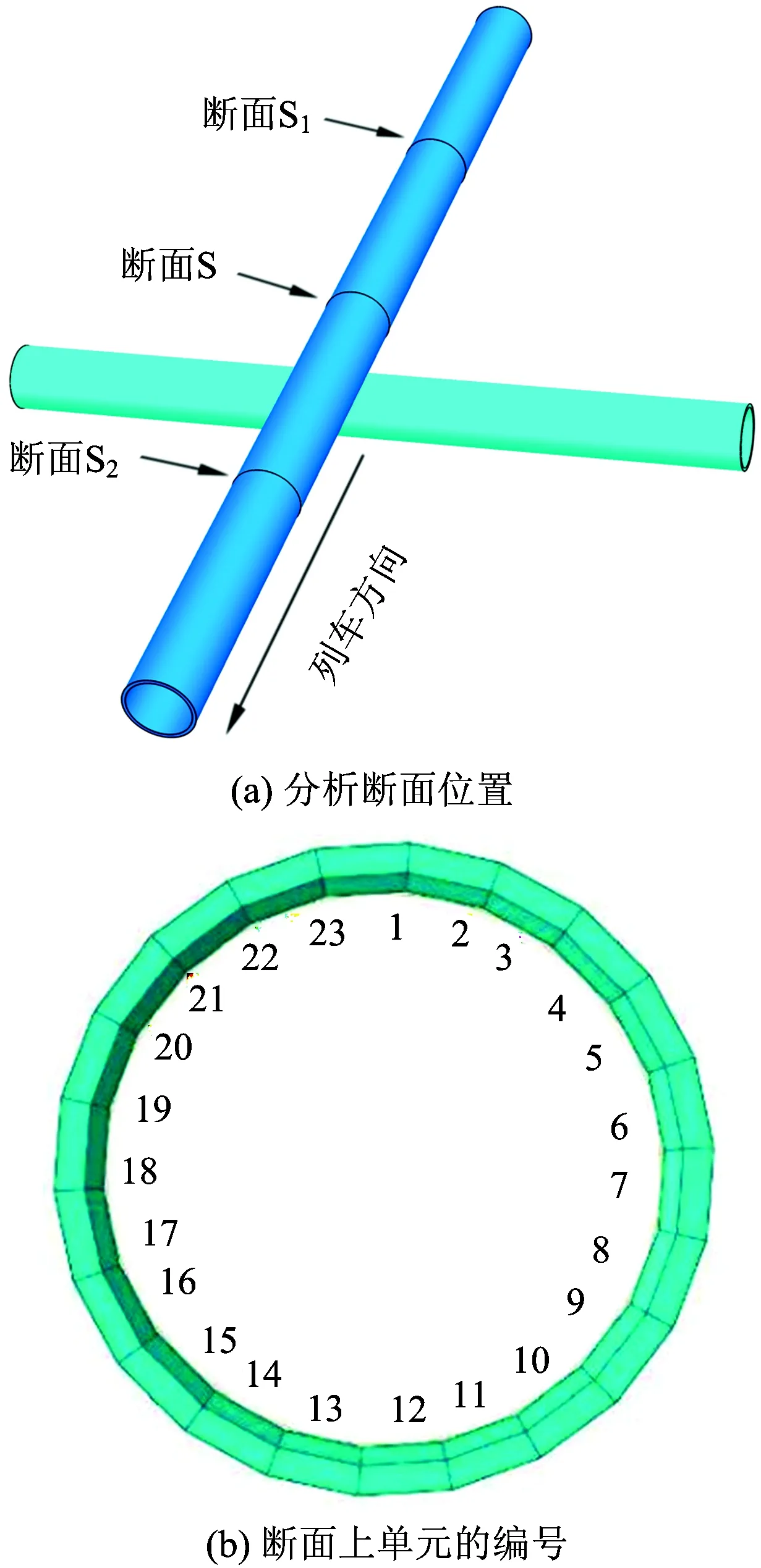
图8 监测断面及其单元位置示意图
(3)随着上下隧道净距的减小,上部隧道沿纵向各分析断面的各个位置的压致损伤均有所增加,同样拱脚和拱底的压致损伤较大。对于断面S,在上下隧道净距为2 m时,拱底压致损伤峰值达到0.014 3,为净距4和6 m时的1.35倍和1.73倍。
(4)当上下隧道净距为6 m时,远离交叠处的上部隧道断面S1和断面S2的拱顶附近均未出现压致损伤,而当上下隧道净距为2和4 m时,两处均出现较小的压致损伤,其中断面S1拱顶的压致损伤峰值分别为0.000 24和0.000 08,断面S2拱顶的压致损伤峰值分别为0.000 25和0.000 08,断面S拱顶在上下隧道净距为6 m时已出现压致损伤,其峰值为0.000 4,在上下隧道净距为2和4 m时,压致损伤峰值到达0.000 52和0.000 43。
从图10中可得如下结论。
(1)分析断面上拉致损伤的分布规律与压致损伤近似,且在数值上更大,同样在交叠中心处受到下部隧道影响也具有放大效应。
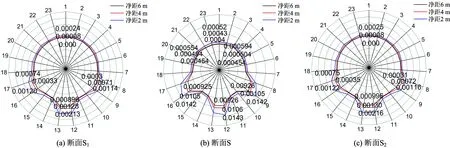
图9 压致损伤分布图

图10 拉致损伤分布图
(2)随着上下隧道净距的减小,上部隧道沿纵向断面各个位置的拉致损伤均有所增加,且拱脚和拱底的拉致损伤较大。在交叠中心处断面S的拉致损伤最大,其拱底拉致损伤在上下隧道净距为2 m时达到峰值,为0.105,约为净距4和6 m下断面S1、断面S2拱底拉致损伤峰值的1.36倍和1.97倍,且为相同净距条件下远离交叠处断面S1、断面S2拱底拉致损伤峰值的24.31倍和23.97倍。
(3)当上下隧道净距为6 m时,远离交叠处的断面S1和断面S2拱顶附近均未出现拉致损伤,当上下隧道净距为2和4 m时,断面S1和断面S2拱顶均出现较小拉致损伤,断面S1拱顶拉致损伤峰值分别为0.000 57和0.000 21,断面S2拱顶压致损伤峰值分别为0.000 21和0.005 7。对于交叠中心处断面S上的拱顶,在上下隧道净距为6 m时已出现拉致损伤,其峰值为0.000 5,在上下隧道净距为2和4 m时,拉致损伤峰值到达0.003 2和0.001 2。
4 结 论
(1)列车距离分析断面越近,分析断面上隧道衬砌的振动加速度响应越大;在同一横断面上,隧道衬砌的振动加速度表现为拱底最大,拱腰次之,拱顶最小。
(2)列车距离分析点越近,分析点隧道衬砌的振动最大主应力增量响应越大,在交叠中心断面达到峰值;在交叠中心断面处上部隧道的最大主应力增量远大于下部隧道
(3)压致损伤和拉致损伤主要集中在上部隧道底部附近130°的范围内,而在拱顶附近区域不太显著。越接近交叠中心处上部,隧道的压致和拉致损伤均越大,且在交叠中心处达到最大。
(4)随着两个隧道净距的减小,上部隧道的压致和拉致损伤均增大,且拱脚和拱底处的压致和损伤拉致损伤增长幅度较大,交叠中心处断面的压致和拉致损伤的增加幅度要明显大于远离交叠处的断面。因衬砌混凝土本身的受拉敏感性,上部隧道各断面沿衬砌环的拉致损伤要大于压致损伤。
(5)当两个隧道净距为6 m时,仅交叠中心处上部隧道拱顶出现较小的压致和拉致损伤,远离交叠处上部隧道断面未出现压致和拉致损伤。当两个隧道净距分别为4和2 m时,交叠中心处上部隧道压致和拉致损伤增量较大,远离交叠处上部隧道仅出现较小的压致和拉致损伤。
(6)当两个隧道近距离垂直交叠时,下部隧道对上部隧道的振动加速度、最大主应力增量和压致及拉致损伤均具有放大效应。

