灰预测模型在连续梁桥施工监控中的应用研究

袁晓辉，申晓伟

(信阳师范学院 建筑与土木工程学院，河南 信阳 464000)

0 引言

目前桥梁工程正朝着大吨位、大跨度方向不断发展，因此对大跨度连续桥梁进行施工监测与控制，是确保桥梁施工过程安全的一种重要手段.已有的施工控制理论主要有灰色系统理论、神经网络、设计参数识别与调整、Kalman滤波法、最小二乘法等[1].其中，灰色系统理论[2]是在1982年由华中科技大学邓聚龙教授首先提出,并创立了一门新兴学科，随后被应用于各行各业中去.20世纪90年代初灰色系统控制理论被应用于大跨度连续桥梁中并被广大专家学者所认可.包龙生等[3]为了得到正确的预拱度求解方法，采用灰色系统理论，建立了GM(1,1)模型对连续梁桥预拱度进行预测，结果表明采用灰色系统理论GM(1,1)模型可以准确地对连续梁桥预拱度进行预测；孙志伟等[4]采用灰色预测理论建立了竖向预应力长期损失GM(1,1)模型，探讨了竖向预应力长期损失规律，并提出竖向预应力施工中锚下应力控制标准，为无损检测提供参考；姚荣[5]在桥梁施工监控技术中采用两种灰色系统预测模型GM(1,1)和GM(2,1)，对比分析了采用4个、6个样本数据的GM(1,1)模型，并采用4个样本数据的GM(2,1)模型来预测实际工程中的立模标高值，结果表明增加样本数据对提高精度作用小,而增加模型阶数对精度提高较大；王赞芝等[6]应用灰色系统理论，建立了高速铁路斜交连续梁桥预拱度的设置方法，以此方法指导桥梁施工，最终大桥以很高的精度合拢，成桥后的线形和内力满足设计要求；张熙胤等[7]根据GM(1,1)模型提出了GM(1,n)关联预测模型并运用于桥梁控制中，实践结果表明该模型能够准确预测各梁段的高程；曾勇等[8]在层次分析法的基础上提出了基于层次分析法-灰色系统理论-人工神经网络-有限元分析-蒙特卡罗理论的定性、定量风险分析方法并将其应用于大跨单索面公轨两用钢桁梁斜拉桥，结果表明该风险分析方法采用概率理论更加准确地确定了桥梁风险因素对桥梁结构的影响；张谢东等[9]运用灰色系统理论中的新陈代谢GM(1,1)模型建立了温度挠度的预测模型，预测结果表明该模型精度较高，可以用于温度挠度的预测；章继树[10]根据灰色系统理论，采用有限元软件ANSYS建立了主桥有限元模型，通过有限元分析的方法对线形和应力的理论值和实测值进行分析，并与灰色预测值进行对比分析，结果表明施工过程中线形和应力的理论值、实测值和灰色系统预测值均吻合较好.

灰色系统理论借助少量杂乱无章的原始数据，通过数据整理生成规律性强的数列对将要施工的阶段进行预测计算，从而克服了信息不完全的缺点.本文将采用灰色系统理论建立单变量GM(1,1)预测模型，对跨娄新高速铁路连续桥梁悬臂施工过程中的挠度及应力的变化量进行预测，并用预测结果指导现场施工，为同类桥梁施工提供参考.

1 单变量GM(1，1)模型

灰色系统理论[2]是以现有信息和原数据序列为基础，通过灰过程及生成的原始数据进行数据加工与处理，建立含有未知量的微分方程模型.灰色系统理论的主要原理为：以既有的数据信息或原始数列为基础，然后根据原始数列进行数据整理分析并建立微灰色模型，即GM模型，并对施工过程中挠度及应力的发展变化进行预测控制.

灰色系统理论的微分方程模型称为GM模型，G为Grey(灰)，M为Model(模型).GM(1,1)为一阶一个未知量的微分方程模型，GM(1,1)的灰微分方程是：

x(0)(k)+az(1)=u,k=1,2,…,

(1)

式中：a、u为常数，分别叫作发展系数和灰色作用量；x(0)(k)为灰导数，符合白因灰果率；z(1)(k)为x(0)(k)白化背景值；x(1)(k)，x(0)(k-1)为灰导数成分，与灰导数成分符合平射率.

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)=

(z(1)(2),z(1)(3),z(1)(4),…,z(1)(n)),

(2)

GM(1,1)白化微分方程：

(3)

因为灰微分方程x(0)(k)+az(1)=u是以上述方程为模型建立的，所以称上述方程为GM(1,1)的白化方程.式中a，u为未知参数，x(1)(k)为原始数据x(0)(k)累加生成的数据系列.

x(0)(k)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(n))

为GM(1,1)模型的原始数列，经过一次累加生成数列：

x(1)(k)=(x(1)(1),x(1)(2),x(1)(3),…,x(1)(n))x(1)(k)=

经过累加之后，原始数列的规律性增强.求解(2)式得时间响应式：

(4)

对式(4)离散后得响应预测模型：

(5)

令：ε为GM(1,1)数据矩阵方程的残差：

(6)

根据最小二乘法解得参向量:

(a,u)T=(BTB)-1BTYN,

(7)

其中

(8)

根据式(7)求得a和u的值，代入式(4)中,从而求得下阶段x(1)(k+1)，按照这样的方法依次，把得到数列累减还原生成，求得还原预测值：

x(0)(k+1)=x(1)(k+1)-x(1)(k),

(9)

a、u或根：x(0)(k)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(n))是n元原始数列，则x(0)(k)的GM(1,1)模型参数a、u满足下述式子：

2 灰预测模型在桥梁挠度及应力控制中的应用

2.1 工程概况

跨娄新高速铁路特大桥主桥为48 m+80 m+48 m三跨预应力混凝土连续箱梁刚构桥，主桥布置示意图如图1所示.

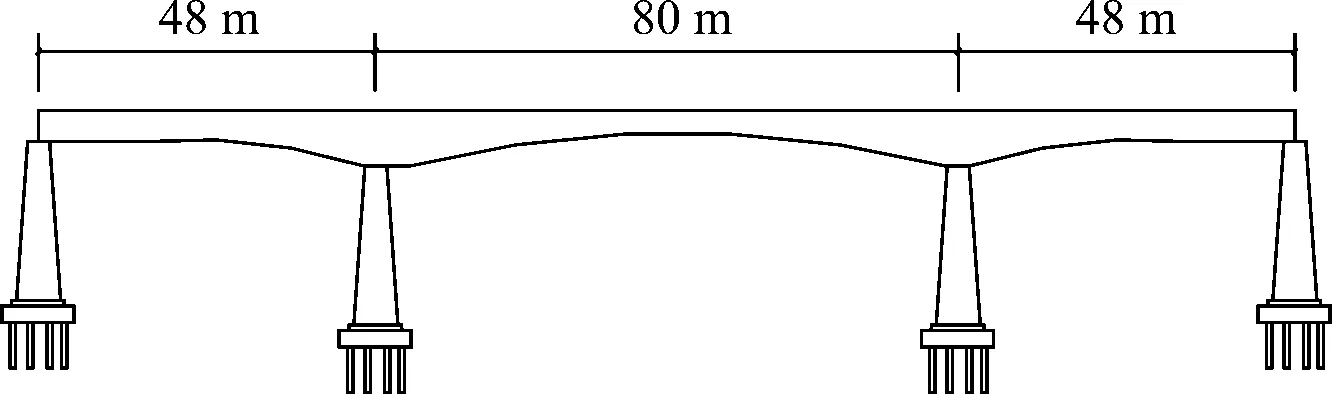
图1 跨娄新高速铁路特大桥示意图Fig. 1 The sketch map of Kua Louxin highspeed railway bridge

梁全长177.5 m，梁底下缘按二次抛物线变化，中支点处梁高6.65 m，中跨跨中9 m，直线段及边跨13.25 m，直线段梁高为3.85 m，边支座中心线至两端0.75 m.梁截面采用单箱单室、变高度、变截面直腹板形式，梁顶板厚度除梁端附近外均为40 cm，腹板厚度48 cm至60 cm、60 cm至90 cm，按折线变化.箱梁顶宽12.0 m，底宽6.7 m.箱梁与主墩10#墩，11#墩形成两个T构，桥梁各梁段截面图如图2所示.

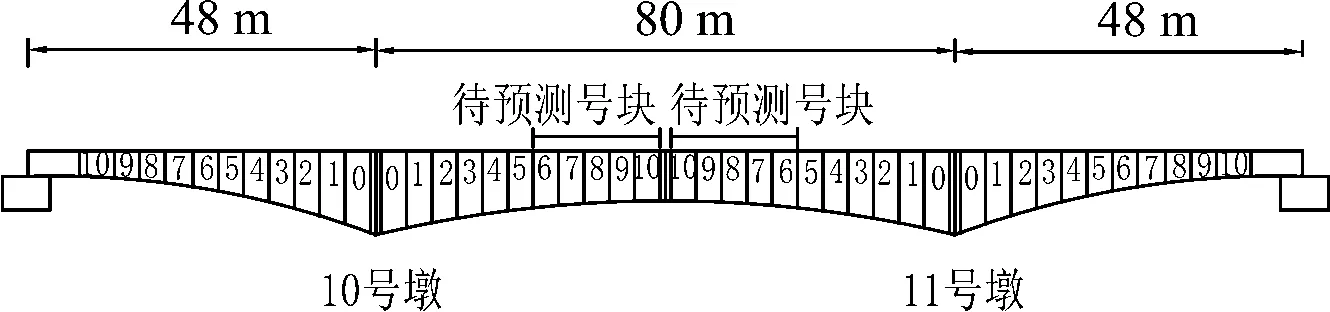
图2 跨娄新高速铁路特大桥各梁段截面图Fig. 2 The each girder section of Kua Louxinhigh speed railway bridge

2.2 线形预测及分析

限于篇幅,仅以跨娄新高速铁路特大桥10#墩小里程6#块施工为例来说明灰色系统理论在实际工程中的应用.首先以10#墩小里程6#块施工完毕后各工况浇筑前后、张拉前后挠度实测值与经过仿真计算理论值之差作为原始数据建立GM(1,1)模型，然后根据灰色系统原理编制Matlab程序进行计算，同理对10#墩小里程6#块施工完毕后各工况浇筑前后，张拉前后应力变化量进行预测，10#墩小里程6#块施工完毕后理论与实测挠度变形值数据如表1所示.

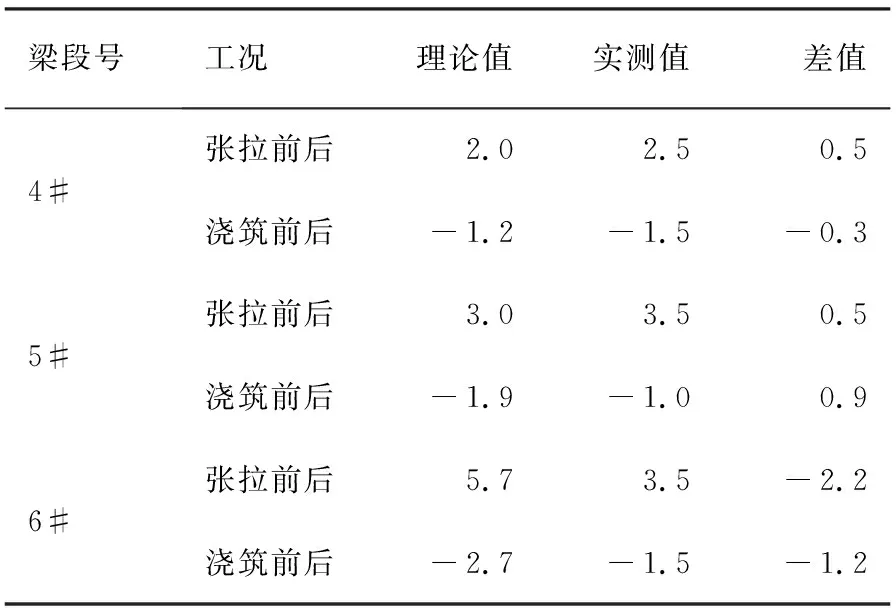
表1 6#块浇筑及张拉后挠度值(mm)Tab. 1 The deflection value of 6# blocks afterpouring and tensioning(mm)

以实测值与理论值之差：

x(0)(k)=(0.5,0.5,-2.2),

作为原始数列建立GM(1,1)模型,原始数列经过一次累加生成数列：

x(1)(k)=(0.5,1.0,-1.2),

进而得：

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)=

(0.8,-0.1).

由式(8)得：

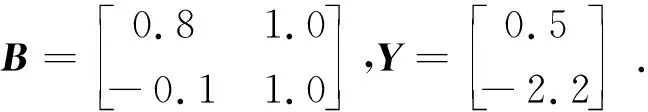
通过Matlab编码计算得：

把a和u代入式(5)得：

x(1)(k)=1.1e-3.2(k-1)-0.6,

所以

x(1)(1)=0.5；x(1)(2)=-0.5,

x(1)(3)=-0.6；x(1)(4)=-0.6.

数据经过还原得：

7#张拉前后理论挠度变形值是4.8 mm，7#张拉后挂篮变形值预测值为：4.8 mm，实测值为5.7 mm.同理浇筑前后预测值，以实测值与理论值之差x(0)(k)=(-0.3,0.9,1.2)为原始数列建立GM(1,1)模型，经过一次累加得：

x(1)(k)=(-0.3,0.6,1.8),

进而得出：

z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)=(0.2,1.2).

把上述数据代入式(3)、式(7)中可以求得：

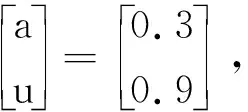
将a和u代入式(5)可以求得：

x(1)(1)=-0.3，x(1)(2)=0.5,

x(1)(3)=1.1，x(1)(4)=1.6.

数据经过累减还原得：

7#浇筑后理论挠度变形值为-2.4 mm，则7#浇筑后预测挠度变形值为-1.9 mm，实测值-1.3 mm，则10#墩6-10#块挠度及应力变化量预测值如表2所示.

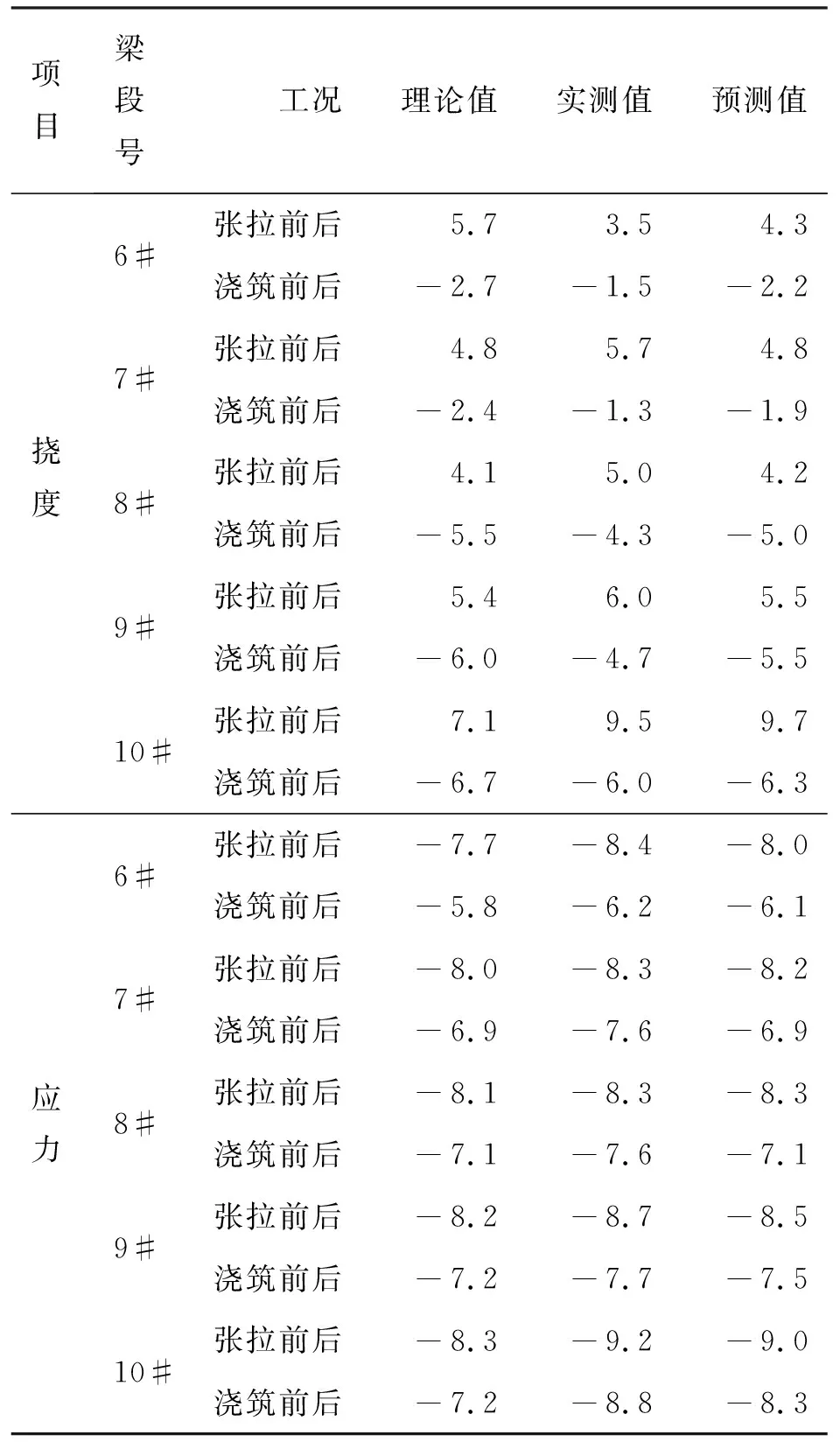
表2 6#-10#块挠度及应力变化量预测值Tab. 2 The deflection predictive value andstress variation of 6#-10# blocks

图3表示的是10#墩小里程张拉前后和浇筑前后挠度预测值、实测值及理论值比较曲线，图4表示的是10#墩小里程张拉前后和浇筑前后应力预测值、实测值及理论值比较曲线，由此可见挠度预测变形值与实测变形值比较接近，误差都在1.0 mm之内，在[s]容许的范围.同时应力变化量的比较曲线吻合度也比较高，表明预测结果可以满足国家规范标准对线形及应力控制的要求，同时也能说明灰色系统理论在连续桥梁施工线形及应力控制中应用的可行性.

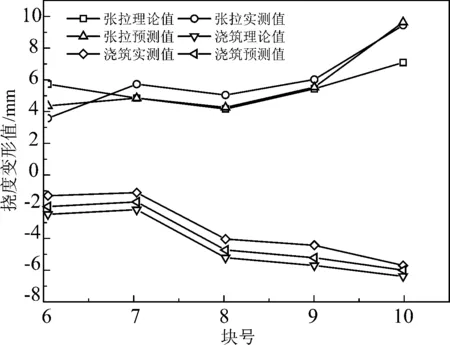
图3 10#墩小里程张拉及浇筑前后挠度值比较曲线Fig. 3 The comparison curves of 10# pier small mileagedeflection value about before and after tensioning and casting

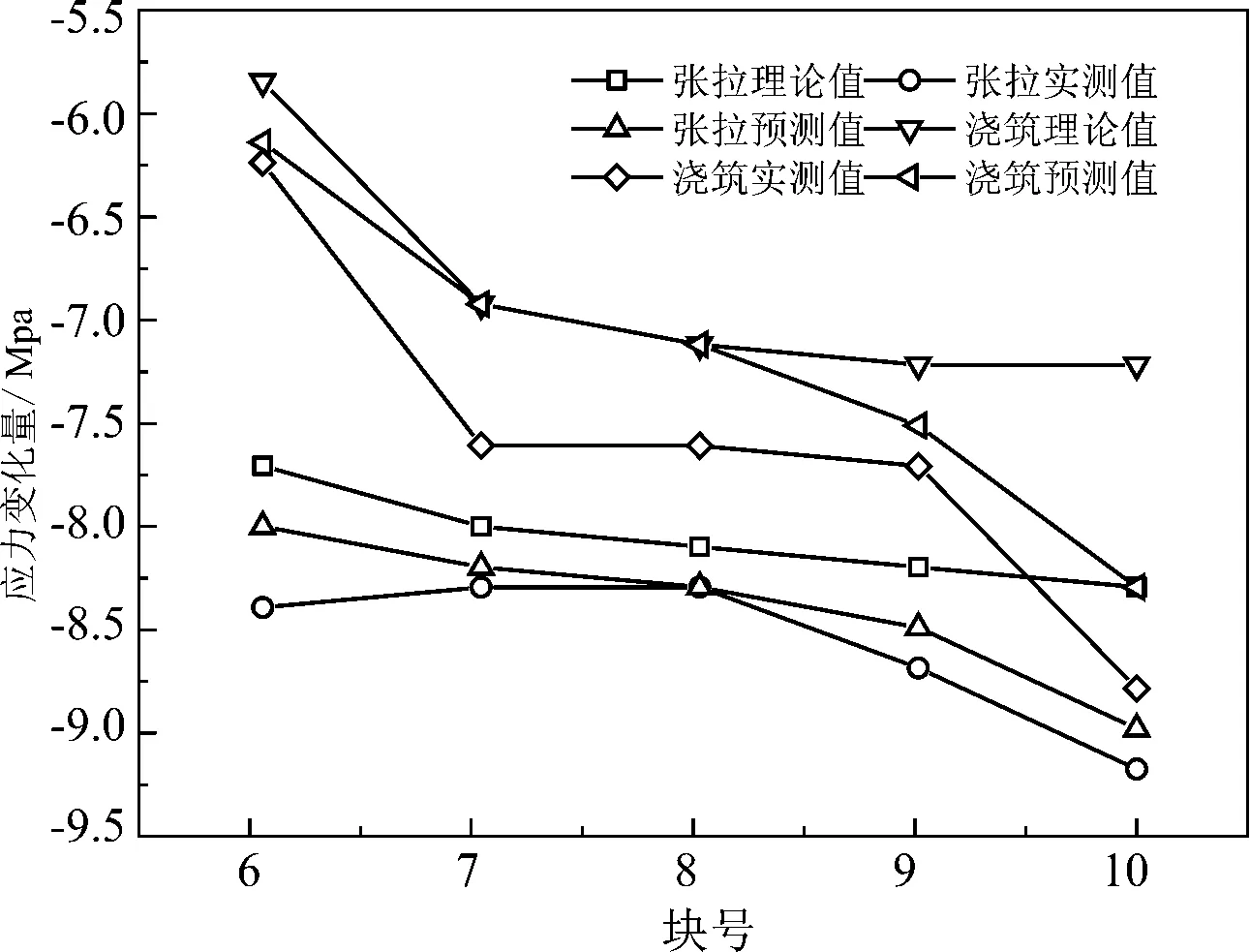
图4 10#墩小里程张拉及浇筑前后应力变化量比较曲线Fig. 4 The comparison curves of 10# pier small mileage stressvariation about before and after tensioning and casting

2.3 成桥结果分析

跨娄新高速铁路特大桥10#墩和11#墩4-10#块成桥线形对比曲线如图5、图6所示.

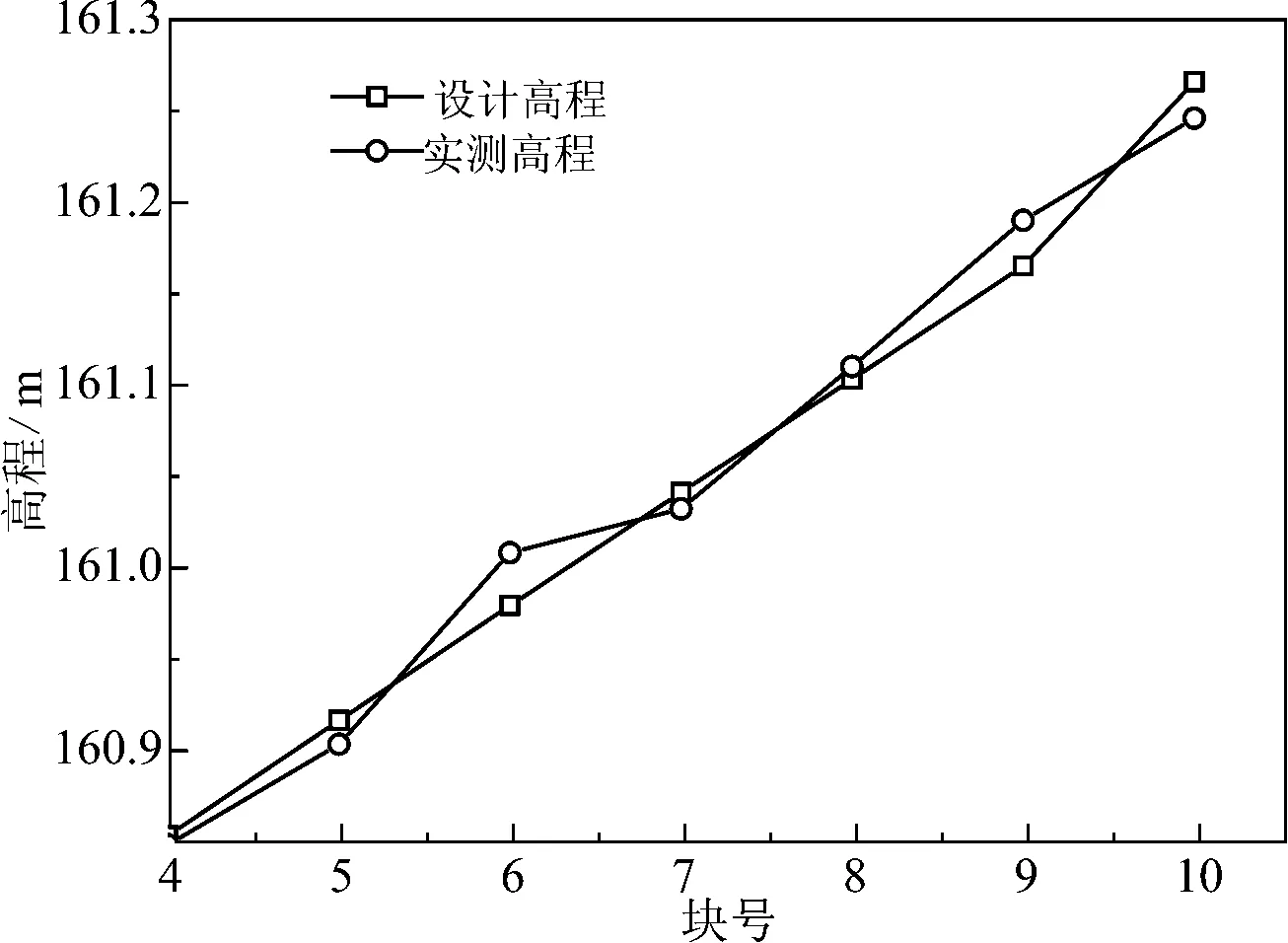
图5 10#墩4#-10#块设计高程与实测高程对比曲线Fig. 5 The comparison curves of 4#-10 # blocks of 10# pierabout design elevation and measured elevation

由图5与图6的10#墩及11#墩4#-10#块设计高程与实测高程对比曲线可以得出设计高程曲线与实测高程曲线吻合度较高，能够保证最终成桥线形与设计线形相统一.

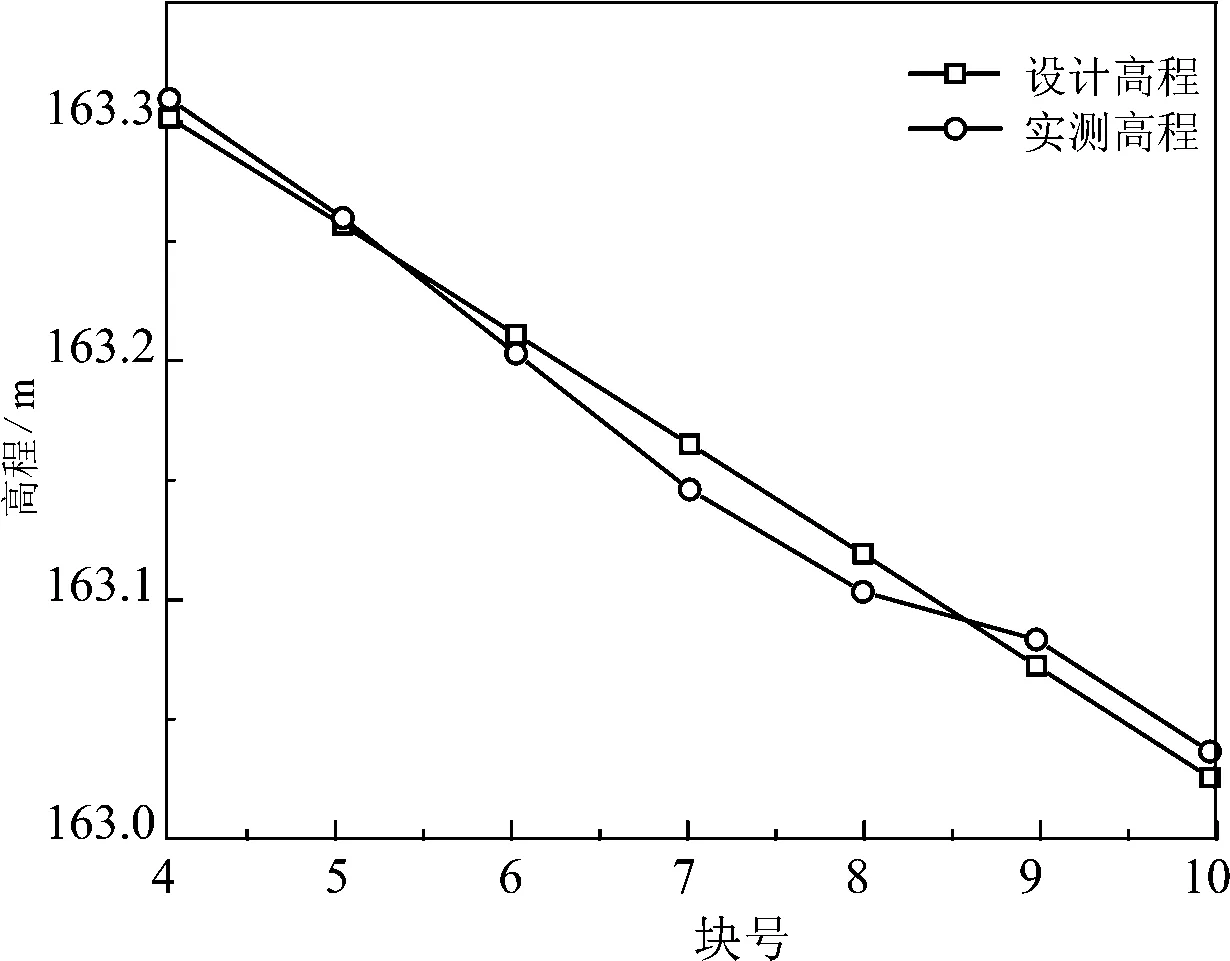
图6 11#墩4#-10#块设计高程与实测高程对比曲线Fig. 6 The comparison curves of 4#-10 # blocks of 11# pierabout design elevation and measured elevation

3 结语

本文以跨娄新高速铁路特大桥为工程背景，运用灰色系统理论建立GM(1，1)瞬态预测模型，同时根据灰色原理编制Matlab程序进行预测计算，预测结果与实测值绘制了对比曲线图.通过对比曲线图得出主要结论：

(1)连续梁桥在悬臂施工过程中挠度预测值与实测值较为吻合，误差保持在1.0 mm左右，确保成桥后的最终线形与设计线形具有较好的一致性.

(2)连续梁桥在悬臂施工过程中应力预测值与实测值较为吻合，误差在国家标准规范的许可范围之内，确保了悬臂施工过程中结构的安全性.