运用割补法求三角形的面积

周小霞

（湖北省黄冈市浠水县第二实验小学，湖北 黄冈）

图1

分析：若直接运用三角形的面积公式求

△OAB的面积，则比较难.我们可以运用间接方法——割补法，求△OAB的面积.

思路1把△OAB的面积转化成几个图形的面积差.

解法 1 因为A（m，6），B（3，n）在的图象上，所以解得

过点A作AC⊥y轴于点C，过点B作BD⊥x轴于点D，直线AC、BD交于点E（如图 1），则四边形CODE是矩形，E（3，6）.

所以S△OAB=S矩形CODE-S△ACO-S△BDO-S△AEB

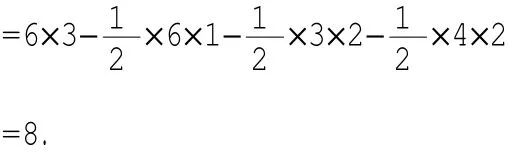
注：本题也可以用以下两种方法求△OAB的面积：

（1）S△OAB=S梯形AODE-S△BDO-S△ABE；

（2）S△OAB=S梯形BOCE-S△ACO-S△ABE.

解法 2 由解法 1 知A（1，6），B（3，2）.

设直线AB交x轴、y轴分别于点C、D（如图2）.

设直线AB的解析式为y=kx+b，

所以AB的解析式为y=-2x+8.

当x=0 时，y=-2×0+8=8，所以D（0，8）.

当y=0 时，0=-2x+8，x=4，所以C（4，0）.

所以S△OAB=S△COD-S△AOD-S△BOC

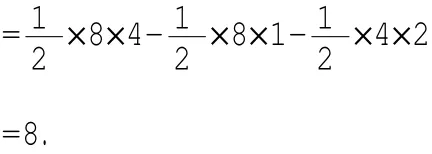
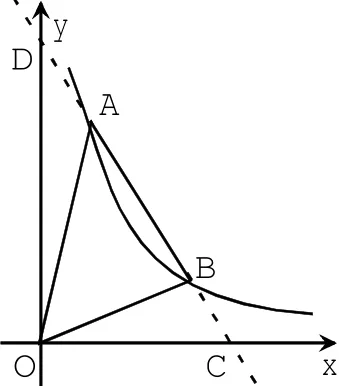
图2

注：本题也可以用以下两种方法求△OAB的面积：

（1）S△OAB=S△ACO-S△BCO；

（2）S△OAB=S△BDO-S△ADO.

思路2把△OAB的面积转化成另一个图形的面积.

解法 3 由解法 1 知A（1，6），B（3，2）.过点A作AC⊥x轴于点C，交BO于点E，过点B作BD⊥x轴于点D（如图3）.

因为S△ACO=S△BDO=3，

所以S△AEO+S△ECO=S梯形BDCE+S△ECO.

所以S△AEO=S梯形BDCE.

所以S△OAB=S△ABE+S△AEO

=S△ABE+S梯形BDCE

=S梯形 ACDB

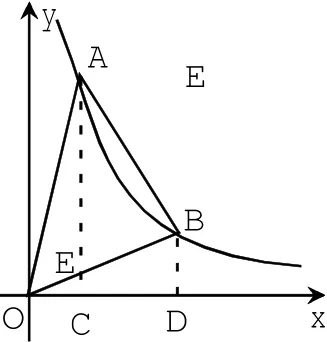
图3

注：本题也可以用以下方法求△OAB的面积；过点A作AE⊥y轴于点E，过点B作BF⊥y轴于点F.S△OAB=S梯形ABFE.

思路3把△OAB的面积转化成几个图形的面积和.

解法 4 由解法 1 知A（1，6），B（3，2）.

过点A作AC⊥x轴于点C，交BO于点E（如图4）.

设直线BO的解析式为y=kx，

则 2=3k，解得

所以BO的解析式为

当x=1时，所以

图4

所以S△OAB=S△AEO+S△AEB

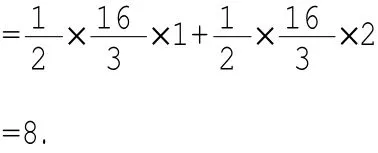
注：本题也可以用以下方法求△OAB的面积：过点B作BD⊥y轴于点D，交AO于点F.S△OAB=S△BFA+S△BFO.