基于MRAS的IPMSM速度自适应全阶状态观测器的设计

黄 韬

(厦门理工学院现代工程训练中心，福建 厦门 361024)

与表贴式永磁同步电动机(SPMSM)相比，内嵌式永磁同步电动机(IPMSM)不仅具有高功率密度、高效率、高可靠性等优良的动态特性，而且过载能力强，转矩密度大，转子磁钢不脱落。因此，基于IPMSM的调速系统广泛地应用于电动汽车和混合动力汽车中[1-2]。电机调速系统中，速度信号的采集与反馈是必要的。安装在电机转子上的速度或位置传感器可完成电机速度信号的采集，但该传感器价格昂贵，不仅提高了调速系统的成本，而且限制了其在恶劣环境下的应用。无速度传感器技术逐渐成为电机调速领域研究热点。文献[3-4] 分别设计了基于模型参考自适应(MRAS)算法的无速度传感器方法，但这些方法仅采用磁链或者定子电流作为状态变量，受电机参数影响较大。文献[5-6] 研究了基于状态观测器的无速度传感器算法，但其状态观测器的反馈矩阵设计复杂，实现困难。文献[7-8] 将神经网络智能算法应用到无速度传感器控制中，但这类方法目前难以在工程中应用。本文采用在工程实现方面较为简便的MRAS方法进行IPMSM转速辨识，将磁链及定子电流的交直轴分量作为4个状态变量设计出速度自适应全阶状态观测器,以提高IPMSM无速度传感器情况下的动态调速性能。

1 全阶状态观测器系统设计

在转子旋转dq坐标系下，内嵌式PMSM电压方程[9]为

(1)

(2)

对式(1)和式(2)进行移项操作，得到磁链微分方程：

(3)

(4)

式(1)～(4)中：ud和uq分别为直轴和交轴的定子电压分量；Rs为定子电阻；id和iq分别为直轴和交轴的定子电流分量；ψd和ψq分别为直轴和交轴的定子磁链分量；ωr为IPMSM的转子转速。

内嵌式永磁同步电动机绕组自感交直轴分量不等(即Ld≠Lq)，定子电流微分方程[10]为

(5)

(6)

在IPMSM的DTC系统中，为构建MRAS自适应观测器，选择状态变量X=[idiqψdψq]T，DTC系统中实际观测量为定子电流和电压，所以输入量和输出量分别为U=[uduq1]T和Y=[idiq]T。整理可得系统的状态方程：

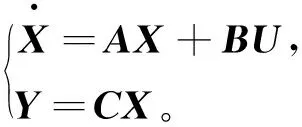
(7)

由式(7)构建全阶状态观测器，各系数矩阵定义如下：

由定子电流观测误差构成校正项(误差补偿器)，状态观测器可用下列方程描述：

(8)

式(8)中：Is和式(7)中的Y相对应，其他定义如下：

观测器状态矩阵A是转速ωr的函数，状态方程(7)实际为时变非线性方程。但因电动机的机械时间常数大于电气时间常数，相对电气变化而言，ωr是缓慢变化的，这种假设在电动机实际运行中基本可以成立，因此式(7)描述的是一个线性缓变系统。在数字化控制中，每个采样周期内，可认为矩阵A的参数是恒定的。

2 速度自适应全阶状态观测器的设计

图1 具有速度自适应全阶状态观测器的MRAS原理图Fig.1 Schematic diagram of MRAS with adaptive full-order observer

速度自适应全阶状态观测器的MRAS原理如图1所示。图1中，参考模型和状态观测器皆为4阶系统，其中IPMSM参考模型由式(7)得出，全阶状态观测器如式(8)所示。本节从状态观测器的稳定性出发，研究全阶观测器中的可调变量ωr，完成转速自适应律的设计。

在MRAS系统中，状态观测器的稳定是指状态误差的动态特性是渐近稳定的，误差能够以较快的速度收敛于零[11]。由式(7)和式(8)可得误差动态方程：

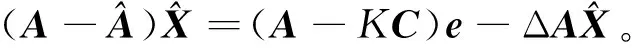
(9)

ΔA为误差状态矩阵，有

(10)

利用李雅普诺夫稳定性理论分析观测器误差的动态稳定性。由李雅普诺夫函数V给出非线性系统渐近稳定的充分条件，而这个函数必须满足连续、可微、正定等要求，将这个函数定义如下：

(11)

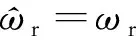
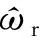
(12)

式(12)中:ωr缓慢变化，可认为其为常数。将式(9)代入式(12)，得：

(13)

因为e呈衰减趋势，所以de/dt小于0，即式(13)中第1项总是负值，只要第2项和第3项之和为零，就可保证dV/dt负定，即：

(14)

(15)

于是，有：

(16)

可得：

(17)

令

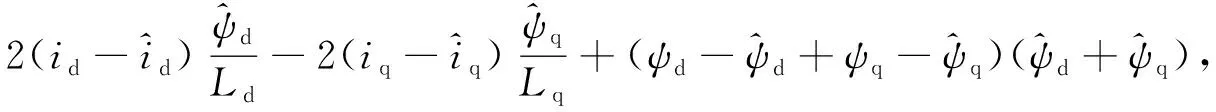
(18)

(19)

令Ki=λ/2，p为微分因子,则有：

(20)

3 仿真实验

为便于仿真，给出一种传统直接转矩控制与本文设计的速度自适应观测器结合的电机控制系统框图，如图2所示。DTC系统利用2个滞环比较器分别控制定子磁链和转矩偏差。在进行坐标变换时，位置信号θr由转速信号积分得到。

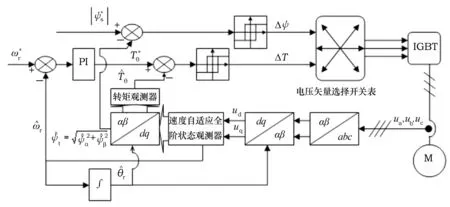
图2 电机控制系统框图Fig.2 Block diagram of motor control system

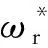
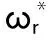
表1 电机控制系统参考速度变化表Table 1 Changes of reference speed in motor control system

仿真1 s后，得到图3～6所示图形。图3为全阶状态观测器的磁链输出值观测图，横轴为磁链矢量在定子静止坐标系下α轴分量，纵轴为β轴分量，由图3可知，电机在低速、额定速度下可正常运行。图4为电机转子实际转速与估计转速仿真结果比较图。由图4可知，基于开关表的DTC控制在所设计的全阶状态观测器作用下，能够使得电机转速收敛于参考转速，但是在起动阶段脉动较大。图5为参考转速为150 r·min-1时的实际转速与估计转速比较曲线图。由图5可以看出，观测器在低速情况下具有良好的跟随性能。图6为电机转子位置与估计位置曲线图。由图6可知，由设计方法得出的电机转子估计位置可较好地跟随电机转子的实际位置。

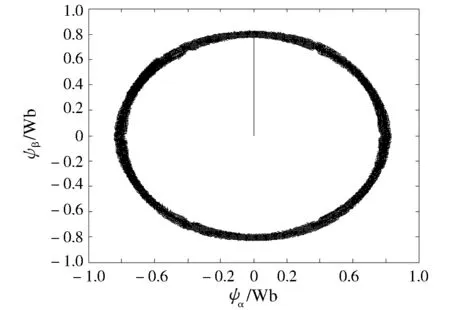
图3 状态观测器磁链输出值观测图Fig.3 Observation of flux is the output of state observer

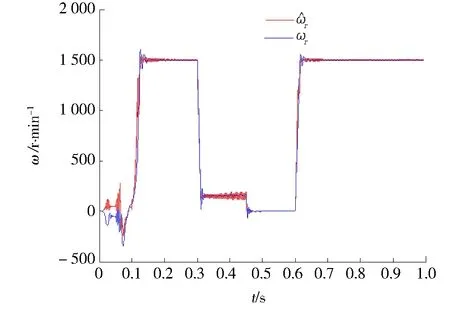
图4电机转子实际转速与估计转速比较图 Fig.4 Actual and estimated rotor speeds compared

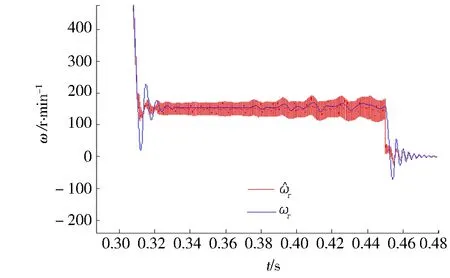
图5 参考转速为150 r·min-1时的转速比较曲线Fig.5 Speed curve when the reference

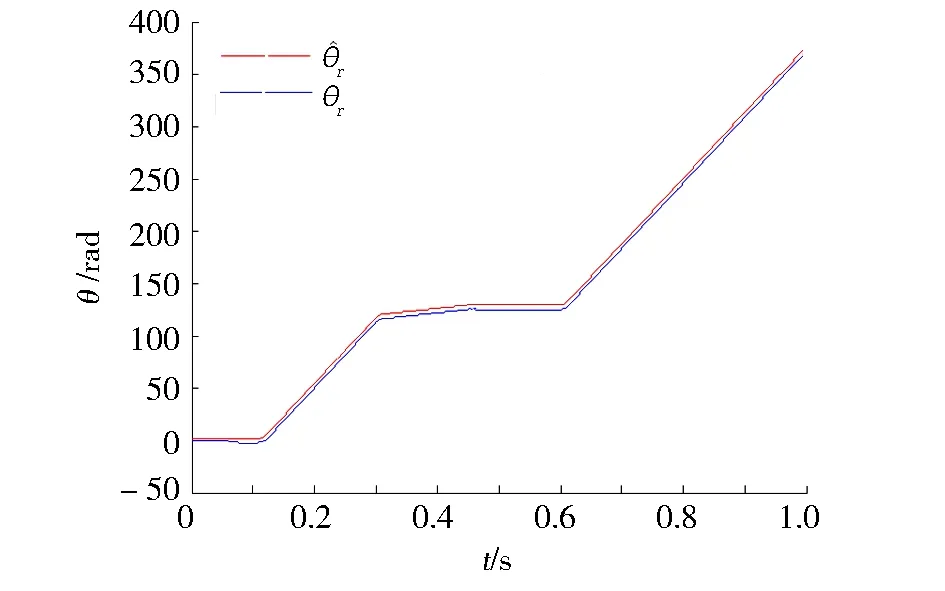
图6 转子实际位置与估计位置比较曲线Fig.6 ctual and estimated rotor positions compared

4 结语

本文以定子磁链和电流作为状态变量，结合MRAS方法设计出速度自适应的全阶状态观测器。通过仿真实验验证可知，由观测器构建的IPMSM直接转矩控制系统不仅在工程中实现便捷，而且在高速和低速情况下，转速和转子位置跟随性能良好，具有较好的动态和稳态性能。该方案可应用于低成本IPMSM伺服控制器研制，在位置及速度精准控制方面有极大的推广价值，后续研究将应用该方案在电信基站隐患识别系统中实现隐患精准跟随功能。