正交空间调制系统的性能分析
黄福春,罗家兵,李 澥,刘雪花
(广州大学华软软件学院计算机系,广东 广州 510990)
随着经济信息社会的不断发展,移动通信技术从第一代到第四代不断更新,人们对高速多媒体无线通信的需求在迅速增长。多输入多输出(multiple-input multiple-output ,MIMO)技术能够满足高速率需求的无线通信技术,如何有效地运用有限的多根天线提升频谱效率的同时,减少误码率成为无线通信领域的一个热点研究方向。
为了满足下一代高速率无线通信网络的需求,Wolniansky等[1]提出了垂直-贝尔实验室分层空时码(V-BLAST)方案,但是该方案在接收端存在检测复杂度和信道间干扰等问题。 Mesleh等[2]把调制技术和空间天线相结合,提出了一种新颖的、更有效的物理层技术,即空间调制技术(space modulation,SM),该技术解决了V-BLAST方案的缺点,明显地降低了信号检测复杂度、避免了信道间干扰和同步问题。Mesleh等[3]提出了SM改进方案——正交空间调制(quadrature space modulation,QSM)技术,有效地提高了频谱效率,增强了通信性能;Afana等[4-5]把QSM方案应用于协作通信技术领域,使该方案得到进一步扩展应用。为解决QSM方案用于大规模天线调制时复杂度相对较大的问题,文献[6-7] 等提出了压缩传感算法,降低了接收端检测复杂度。本文分析了频谱效率和成对错误概率,以及最小欧式距离等主要性能,推导出历经瑞丽分布和高斯白噪声信道的QSM方案的平均误比特率的表达式。
1 QSM系统模型
在QSM方案中考虑Nt×Nr的MIMO系统,Nt为发射天线数,Nr为接收天线数,M表示传统调制符号的调制阶数,QSM发送端模型如图1所示。
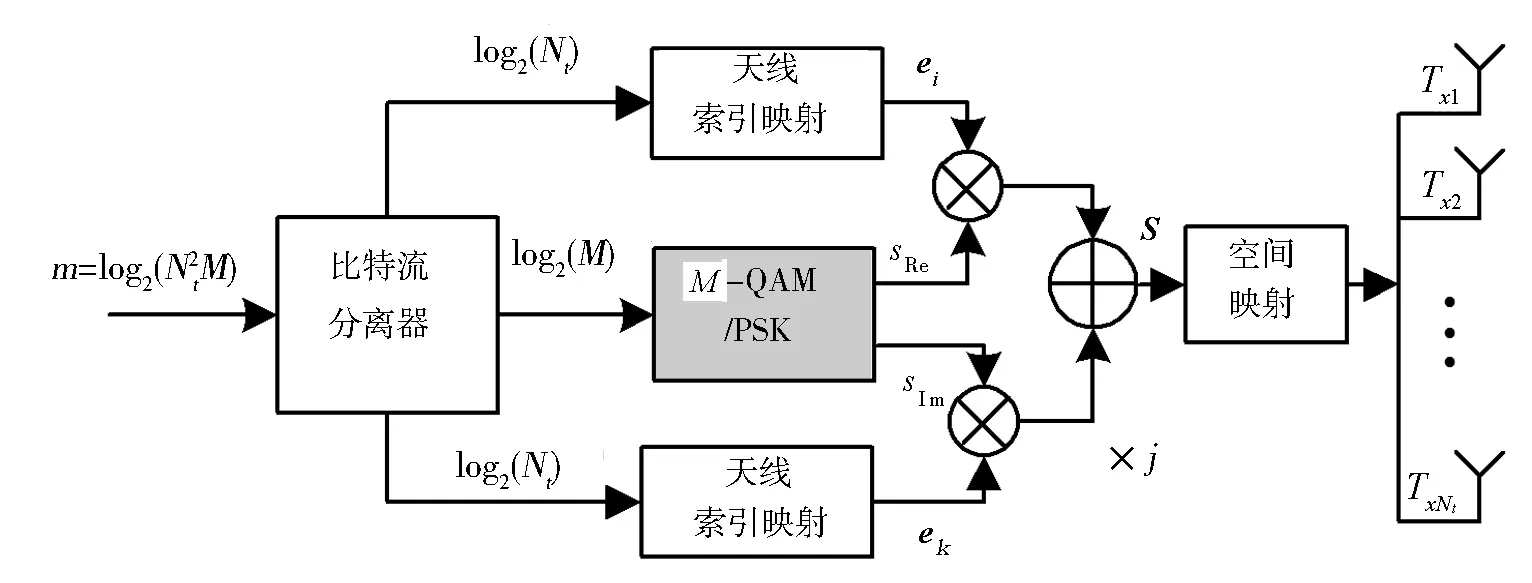
图1 QSM发送端模型Fig.1 System model of QSM transmitter
最后,通过把两者实部sRe·ei和虚部sIm·ek相加,得到一个发射空间向量S,
S=sRe·ei+j·sIm·ek。
(1)
假设发射的空间向量S经过服从频谱平坦瑞丽分布的无线信道Nr×Nt维H和受到加性高斯白噪声Nr×1维的N干扰,到达目的接收端,则接收信号Y可以描述为
Y=HS+N=H·(sRe·ei+j·sIm·ek)+N。
(2)
式(2)中:Y∈CNr×1,N∈CNr×1,H∈CNr×Nt。其中H为信道增益矩阵,表示为
(3)
(4)
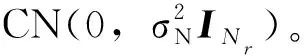
在理想信道估计和最大似然检测(Maximum Likelihood,ML)条件下,我们有
(5)
2 性能分析
2.1 频谱效率
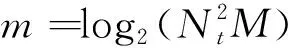
(6)
2.2 成对错误概率分析
首先,通过计算条件成对错误概率的期望值之后,才能计算平均误码率。
(7)
其中:S=[S1,…,SNt]T;Q(·)表示高斯Q函数。
然后针对式(7)的H信道矩阵进行期望为
(8)
基于矩量母函数[8]的方法,式(8)期望的成对错误概率可以计算为
)Nrdθ。
(9)
其中:E{·}表示计算平均值的函数。基于式(9),并通过众所周知的上边界技术得到QSM的平均错误概率为
(10)

2.3 最小欧氏距离


表1 不同频谱效率情况下平方欧氏距离的最小值Table.1 The Squared minimum Euclidean distance at different spectral efficiency
由表1进一步分析可得,在相同频谱效率情况下,由于QSM方案利用空间天线传输更多额外比特,进而降低调制阶数。与SM方案相比,QSM方案相对性地增大了发射空间符号间最小欧氏距离。
3 仿真分析
通过Monte Carlo进行MATLAB仿真,验证上述理论的推导。假设随机产生5×106bit经历瑞丽独立同分布衰落信道和受到白噪声干扰,瑞丽信道和白噪声分别服从独立同分布的0均值单位方差为1和0均值σ2方差的复高斯随机变量。在接收端中,使用ML检测器恢复源信息比特。
在相同频谱效率情况下,QSM方案的空间域传输更多额外信息,以致调制阶数变小,最小欧式距离相对的变大。如图2所示,[Nt,Nr] =[4,4] 情况下,相同频谱效率时,QSM方案所使用的调制阶数都比SM方案小,符号间最小欧式距离相对变大了。因此,QSM方案有更好的误比特率性能。如η=6 bit·s-1·Hz-1条件下,在误比特率为10-3处,与使用16QAM调制方式的SM方案相比,使用4QAM调制方式的QSM方案获得多于2 dB 信噪比增益。[Nt,Nr] =[4,6] 情况下,最小欧式距离没有变,而是增大了接收天线。相比SM方案,QSM方案获得更多接收分集增益。比如,同样频谱效率η=6 bit·s-1·Hz-1,在误比特率为10-3处,使用4QAM调制方式的QSM方案获得多于3.8 dB信噪比增益。在η=7 bit·s-1·Hz-1情况时,有相同的结论。
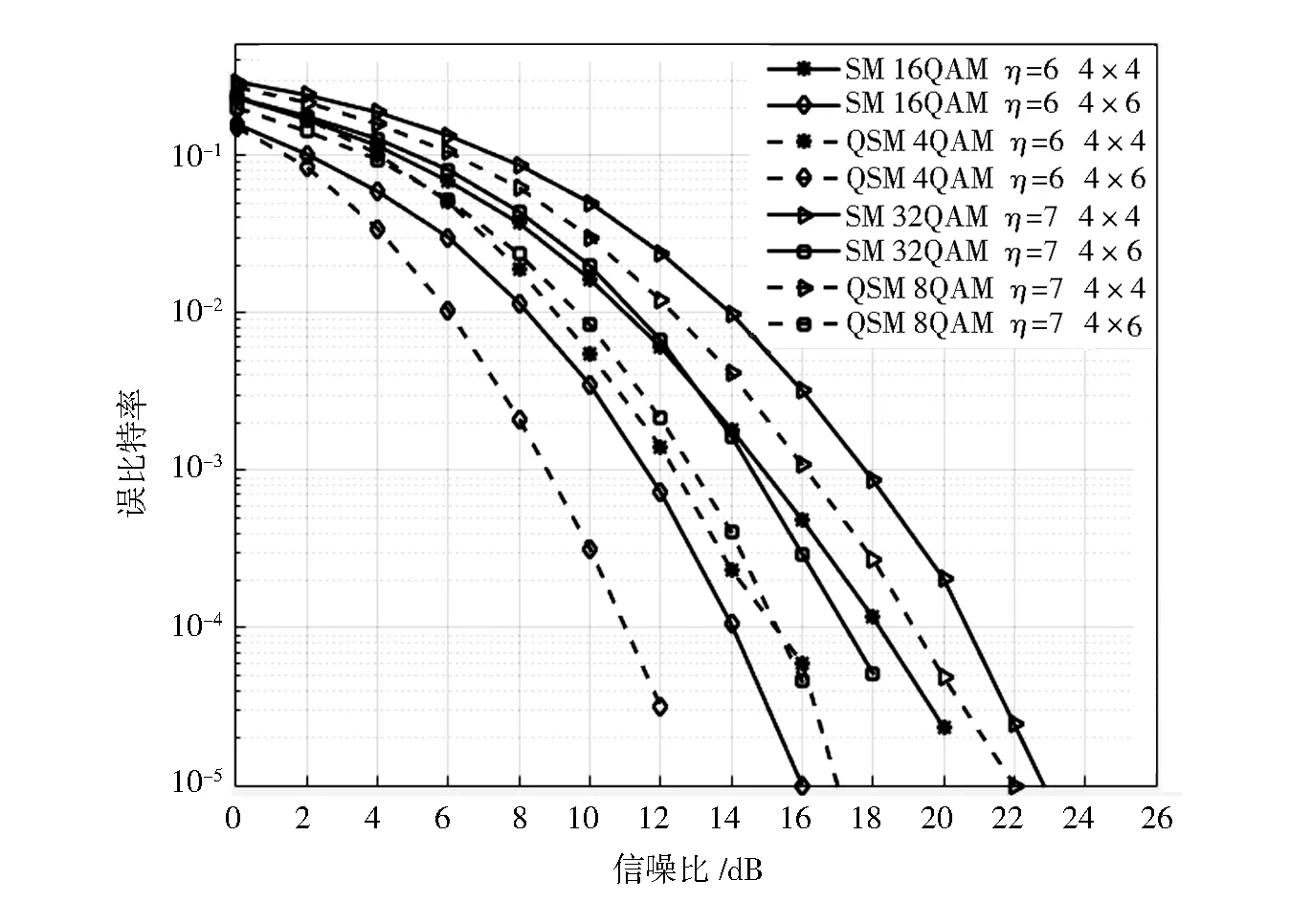
图2 在[Nt,Nr] ={[4,4] [4,6] }情况,SM方案与QSM方案的性能比较Fig.2 Performances of SM and QSM compared with [Nt,Nr] ={[4,4] [4,6] }
从图3仿真曲线可以看出,当发射天线增大时,与SM方案相比,QSM方案能够传输更多额外信息比特,这样能够进一步相对地减小调制方式的调制阶数。因此,QSM方案能够进一步增大最小欧氏距离,获得更好的误比特率性能。如,η=8,9 bit·s-1·Hz-1,[Nt,Nr] =[8,4] 情况,与SM方案相比,在误比特率为10-3处, QSM方案获得多于3 dB 信噪比增益。
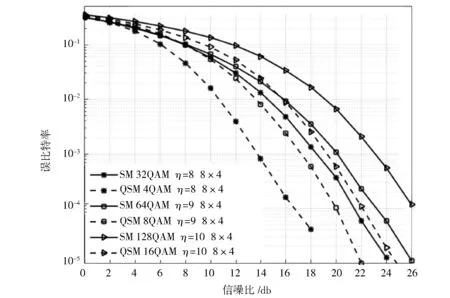
图3 在[Nt,Nr] =[8,4] 情况下,SM方案与QSM方案的性能比较Fig.3 Performances of SM and QSM compared with [Nt,Nr] =[8,4]
4 结语
正交空间调制技术作为一种多天线传输的MIMO技术,具有其性能优越性。将一个传统的调制符号的实部和虚部分别调制在不同的空间天线索引上,使MIMO系统获得分集增益。在QSM方案系统模型的基础上,详细地分析QSM方案的传输速率和成对错误概率性能,列出了不同传输速率下的最小欧式距离。在理想信道估计和最大似然检测条件下,通过MATLAB仿真验证了理论推导的准确性,在相同频谱效率时,QSM方案的性能比SM方案的性能具有很大优势。
由于QSM方案的发射天线数必须为2的幂,Younis等[9]提出了广义空间调制(generalized spatial modulation,GSM)方案,GSM方案天线数量不必与2次方成正比关系,而且采用多于一根天线处于发射状态,这样能够获得空间分集和复用增益。可以将GSM思想用于QSM方案中,解决QSM技术用于大规模天线时复杂度增加的缺陷。再者,挖掘空间天线的空间域和增大空间向量符号间最小欧式距离是进一步提高移动通信的网络性能的手段。

