离心泵壳铸造凝固过程应力场模拟
杨继伟,刘宝惜,范世超,周文龙,郝 海
(1.大连华锐重工铸钢有限公司,辽宁大连 116035;2.大连理工大学,辽宁大连 116024)
在铸造过程中,裂纹和变形是铸钢件尤其是大型铸钢件中普遍存在的铸造缺陷,给工业生产造成了巨大损失。铸造凝固过程中产生的热应力是由于铸件在冷却过程中各部分冷却不均匀,在同一时刻各部分收缩量不同,受阻碍而产生的。当最大应力超过铸件在该温度下的最大抗拉强度,而此时液态金属的补缩又不充足时,可能导致铸件产生变形或裂纹,局部残余应力的存在可能导致零件使用寿命变短。因此,对铸件凝固过程中进行热应力数值模拟,可以有效研究和预测热裂,为实际生产提供科学指导[1,2]。目前,应力场模拟以成熟的温度场数值模拟技术作为基础,对应力场分析时需要综合运用流体流动、热传递、材料高温力学性能分析等技术[3]。ProCAST软件对铸造过程中的热应力模拟主要分为固液两相区的应力分布模拟和凝固以后的数值模拟两部分,目前凝固过程中的应力数值模拟主要集中在凝固以后阶段[4]。
本文以一种308L不锈钢离心泵泵壳铸件为例,利用ProCAST有限元铸造模拟软件对其铸造过程进行数值模拟,研究了在应力场下浇注时间和浇注温度对铸件有效应力的影响,从而为确定最佳工艺方案,优化铸造工艺参数,确保铸件质量,缩短产品试制周期,降低生产成本提供科学依据。
1 数值模拟前处理
1.1 力学模型和热学边界条件
1.1.1 力学模型
目前热应力数值模拟主要采用热弹塑性模型,默认材料屈服前为弹性,屈服后为塑性,弹性模量与屈服应力是温度的函数,且当材料接近熔点时,弹性模量与屈服应力均变为零。本文研究采用ProCAST软件中提供的热弹塑性模型。
热应变增量包括温度变化产生的收缩以及弹性模量和线膨胀系数随温度变化而引起的增量,可以表示为:

式中,T0是初始温度;T是瞬时温度;α是线膨胀系数。
塑性应变增量的大小和方向由流动准则确定:

式中,H′为材料的塑性硬化模量,可由简单的拉伸曲线得到。由以上各式可得出热弹塑性模型的本构方程:
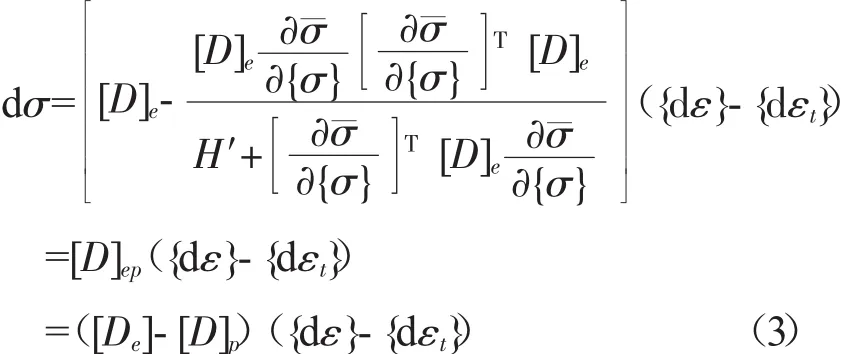
1.1.2 热学边界条件
建立铸件、型壳及环境相互之间的传热模型是对熔模铸件凝固过程进行数值模拟的前提。浇注后,铸件、铸型和环境之间存在动态复杂的换热过程:在铸件、型壳及其二者之间的界面处,保温毡、砂箱及其二者之间界面处,热量(ΔQ)依靠热传导形式进行传递:

式中,h为界面换热系数;T1和T2分别为界面两侧的温度。在型壳表面,铸件及砂箱表面与环境之间存在辐射和对流换热,在铸件冒口与环境之间也存在辐射和对流换热过程:

式中,h1表示模壳或者砂箱等表面与环境的对流换热系数;T表示模壳或者砂箱等表面的温度;Ta表示环境温度;ε表示辐射换热系数;σ为斯蒂芬-玻尔兹曼常数[5]。
1.2 几何模型建立及有限元网格划分
所模拟的铸件是大型离心泵泵壳,材质是308L铸造不锈钢,铸件轮廓尺寸为2817mm×2235mm×1870mm,重量为 21.58t,壁厚大于80mm且不均匀。该铸件工作环境较差,由于壳体结构复杂、壁厚不均匀,对铸造工艺提出很高要求,要能够保证铸件没有裂纹、缩孔和较大变形等缺陷[6]。本文采用三维建模软件UG对铸件进行三维实体造型,并通过prt格式软件与ProCAST之间进行数据转化[7]。铸件采用开放型的底雨淋式浇注系统,铸件三维实体造型如图1所示。

图1 三维有限元模型
因为铸件为对称结构,取1/2进行模拟。实体模型有限元体网格单元总数为751935个,节点总数为98490个,网格划分结果如图2。

图2 三维有限元网格划分
1.3 材料参数设置
模拟铸造过程需要大量材料热物性参数和力学性能,这些材料参数值随温度的变化而变化,如果没有准确的随时间变化的函数关系,很难得到准确的模拟结果[8]。
铸件材料为308L,热物性参数主要来自Pro-CAST自带的材料数据库,其中比热容和屈服强度由JMatPro分析软件计算得到。铸件与壳型之间界面换热系数随两者温度变化而不同,在温度较高的初期达到一个峰值,随后快速下降,因此较难测量。本文中选取铸型材料为树脂砂,采用均值常数来反映整个铸造过程中的界面换热情况。铸型与铸件之间的界面换热系数为500W/(m2·K)[9];铸件与冷铁之间的界面换热系数为1000W/(m2·K);冷铁与铸型之间的界面换热为500W/(m2·K);浇注温度初步设为1580℃[10]。采用重力铸造,壳型应力类型为刚体,铸件采用热弹塑性模型。

表1 308L的导热系数和比热容
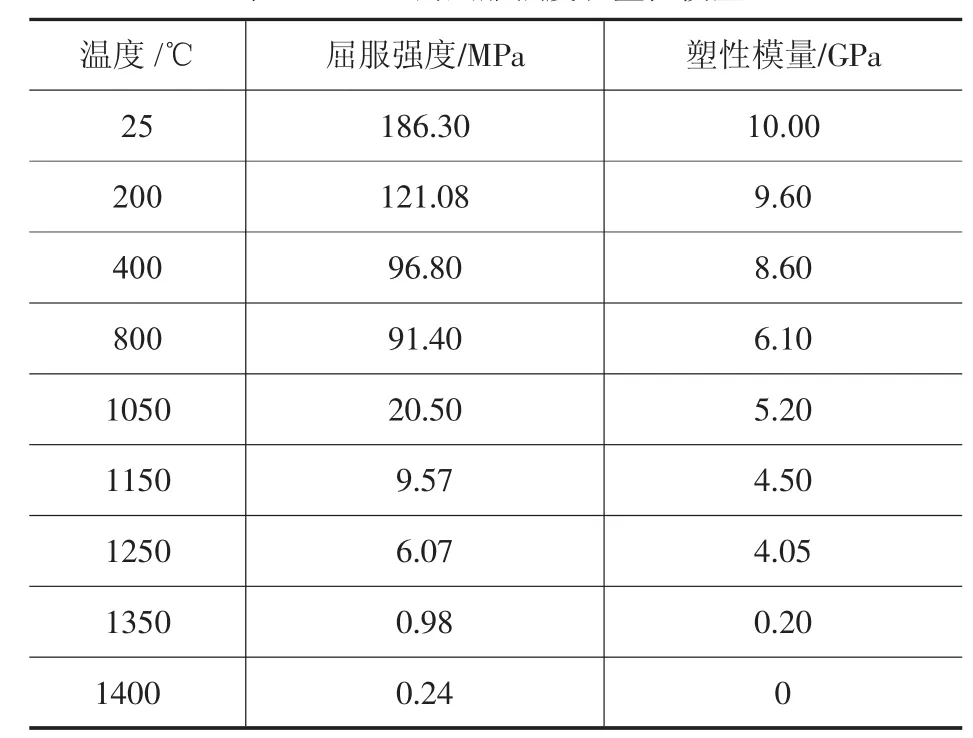
表2 308L的屈服强度和塑性模量
2 模拟试验结果与分析
在收缩应力和热应力作用下,当铸件表面上的最大有效应力大于最大抗拉强度时,就会产生裂纹,本文研究分析从浇注开始至凝固结束时,不同浇注时间和浇注温度对有效应力的影响,从而确定最优工艺路线。
2.1 浇注时间对应力场的影响
选取浇注温度1580℃,以浇注时间分别为100s、120s、140s为模拟对象,图3为不同浇铸时间下,当凝固结束时的有效应力模拟效果图。

图3 不同浇铸时间下的有效应力分布
从图3a中可以看出,浇铸时间为100s时,在浇注过程中铸件最大的有效应力为311.3MPa;从图3b中可以看出,浇铸时间为120s时,在浇注程中最大有效应力为296.7MPa;从图3c中可以看出,浇铸时间为140s时,在浇注过程中最大有效应力为304.3MPa。可以得到结论,浇注时间对于有效应力的影响较小。比较三种不同浇注时间下,浇注过程中的有效应力大小,可以看出120s方案中最大有效应力值较小。从凝固结束时的应力分布来看,120s方案和140s方案均比100s方案中的应力分布更为理想,因此选择“快浇”的120s方案。初步分析得出浇注时间过短,充型速度过快,从而使金属液产生较大的紊流现象,导致有效应力过大。
2.2 浇注温度对应力场的影响
选取120s浇注方案,以浇注温度分别为1530℃、1580℃和1630℃作为模拟对象分析铸件上的等效应力,图4为不同浇注温度下的应力模拟效果图。
从图4a可以看出,浇注温度为1530℃时,在浇注过程中铸件最大有效应力为386.6MPa;从图4b可以看出,当浇注温度为1580℃时,在浇注过程中最大有效应力为296.7MPa;从图4c可以看出,浇注温度为1630℃时,在浇注过程中最大有效应力为258.0MPa。可以得出结论,浇注温度对浇注过程中的有效应力的影响较大,且随着浇注温度的升高,最大有效应力呈下降趋势。但从凝固结束后的有效应力分布来看,1530℃方案中铸件的底部和1630℃方案中铸件的侧壁和底部均产生不同程度的应力集中,所以选取浇注温度为1580℃为最佳方案。
2.3 热裂位置预测
图5是对可能热裂的位置的预测,采用浇注时间120s,浇注温度1580℃的最优工艺方案。可以看出,在整个浇注系统中,在直浇道处存在热裂倾向。分析可知,靠近浇口的铸件部分温度较高,凝固速度比较慢,在凝固阶段末段容易形成强度比较低的薄弱区,从而形成热裂纹。但在铸件主体部位上没有出现热裂倾向。
参考如上工艺,即:底注,浇注时间120s,浇注温度1580℃,得到了无明显缺陷的泵壳铸件,如图6所示。
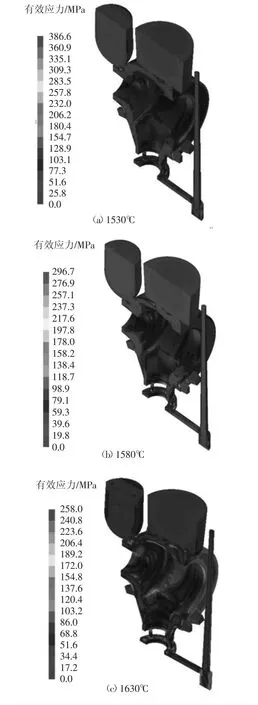
图4 不同浇注温度下的有效应力分布
3 结论
(1)浇注时间对铸件的有效应力影响较小,在浇注过程中,100s方案最大有效应力较大,140s方案次之,120s方案最小且应力分布较为合理。

图6 泵壳铸件实体照片
(2)浇注温度对铸件的有效应力影响显著,适当的增加浇注温度,有利于减小铸件的有效应力。三种方案中,浇注温度为1580℃时,铸件的有效应力分布较为理想且不会出现应力集中现象。
(3)采用浇注时间为120s,浇注温度为1580℃最优方案时,铸件主体部分未出现热裂倾向。

