滚筒凹板筛式花生脱壳机关键部件试验研究及参数优化

王建楠，谢焕雄，胡志超，刘敏基，魏 海，颜建春，吴 峰

(农业部南京农业机械化研究所，江苏南京 210014)

脱壳是花生种植以及油用、食用加工前的必经工序，也是影响花生仁果及其制品品质和商品性的关键[1-3]。我国种用花生大多依靠人工进行脱壳[4-5]，而食用及油用花生多采用卧式滚筒凹板筛式花生脱壳设备进行脱壳。现有的卧式滚筒凹板筛式脱壳设备存在脱壳破碎率高、品种适应性差等问题，致使花生脱壳损失较大，因而脱壳设备难以针对国内纷繁复杂的品种进行全面推广。脱壳滚筒凹板筛组合为此类脱壳设备的关键核心部件之一，其作业参数的设计与优化是脱壳设备作业质量及适应性的重要影响因素。目前，由于对现有脱壳设备的脱壳滚筒凹板筛组合作业参数及相关参数与花生脱壳作业喂料量的优化匹配鲜有研究，使得脱壳滚筒运动参数、滚筒凹板筛间隙与花生脱壳进料量的匹配不合理，脱壳损失较大。本试验对花生脱壳设备关键部件及喂料量进行优化研究，并利用Box-behnken试验设计及响应面分析对关键参数进行优化设计，旨在为花生脱壳机脱壳质量的提升提供理论依据。

1 滚筒凹板筛式花生脱壳机工作原理

1.1 花生脱壳机工作过程

卧式滚筒凹板筛式花生脱壳机(图1-a)在工作时，花生荚果由进料斗进入脱壳仓，在旋转的脱壳滚筒带动下与凹板筛产生挤压、揉搓，从而实现脱壳，脱出的花生仁果与花生壳的混合物经凹板筛落料至振动筛上，凹板筛与振动筛之间安装有风机，在风机的作用下，花生壳与花生仁果、未脱净的花生荚果产生分离，花生荚果与仁果的混合物经过振动筛完成筛分，实现花生仁果及未脱净花生荚果的分离，花生仁果从出料口出料，完成整个脱壳过程。脱壳滚筒结构如图1-b所示，它由两端圆盘与支撑连接杆组成，其中支撑连接杆末端焊接有圆钢，该圆钢可对花生荚果产生揉搓作用；同时可通过调节支撑连接杆的安装尺寸改变滚筒凹板筛的间隙。

1.2 脱壳质量影响因素分析

脱壳滚筒凹板筛组合为花生脱壳机的关键核心部件之一，在荚果脱壳程中脱壳滚筒转速、脱壳滚筒凹板筛间隙、物料进料量均为关键参数，这些关键参数的选择与优化直接影响花生脱壳的破碎率、脱净率。因此，在设计设备时须对相关参数进行优化设计，以降低脱壳过程中的破碎率，提高脱净率。

2 试验材料与方法

2.1 试验仪器设备

试验在自主研发的花生脱壳试验台上开展，以便调节脱壳滚筒凹板筛间隙，并采用变频器(型号H3000)调节脱壳滚筒转速。试验需尺子(精度1 mm)、电子天平(精度1 g)及若干设备参数调整所需辅助工具。

2.2 试验原料

试验所用花生原料为2015年泰州产白沙品种[6]。分别测量500粒花生荚果、500粒仁果的尺寸，结果见表1。

表1 试验对象物理尺寸

2.3 试验考核指标

以花生凹板筛脱出物为考察对象，以脱出物的破碎率(R1)及脱净率(R2)为考核指标，分别通过式(1)、式(2)计算花生脱壳机脱出物的破碎率、脱净率。各试验重复3次，取平均值，参照标准JB/T 5688.2—1991《花生剥壳机 试验方法》开展试验并查样。

(1)

(2)

式中：m为完整纯仁质量，g；m1为破碎仁质量，g；m2为损伤仁质量，g；m3为未剥开果的仁质量，g。

2.4 试验设计

将同品种、同批次、等质量的花生投入花生脱壳试验台脱壳仓，以花生脱壳破碎率及脱净率为考察对象，开展脱壳滚筒转速、脱壳滚筒凹板筛间隙、物料进料量单因素试验研究。

二次回归正交试验：采取中心组合设计方法及理论分析单因素试验结果，以脱壳滚筒转速(A)、滚筒凹板筛间隙(B)、进料量(C)为影响因素，R1、R2为响应值进行响应面分析。按照响应面试验设计对自变量的真实值进行编码，编码方程为

xi=(zi-zi0)/Δzi。

式中：xi为自变量的编码值；zi为自变量的真实值；zi0为试验中心点处自变量的真实值；Δzi为自变量的变化步长[7]。因素自变量编码及水平如表2所示。

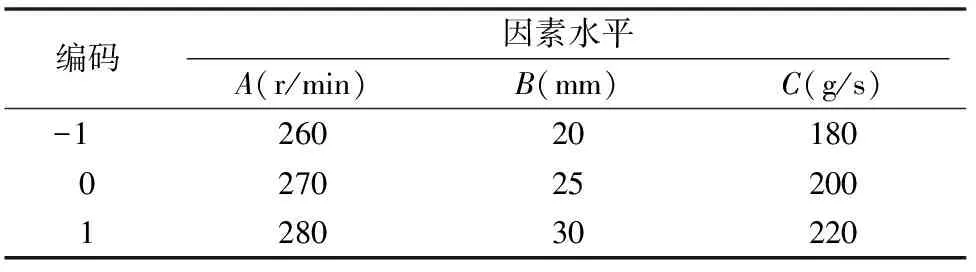
表2 因素编码水平

3 结果与分析

3.1 单因素试验

3.1.1 不同滚筒转速对脱壳质量的影响 根据预备试验结果，将脱壳滚筒凹板筛间隙设定为25 mm，通过振动给料器对脱壳仓料斗均匀供料，使进料量保持在200 g/s。在脱壳滚筒转速分别为245、250、255、260、265、270、275、280、285、290 r/min 的条件下，开展滚筒转速的单因素试验。由图2可知，破碎率与滚筒转速呈现非线性关系，滚筒转速在270、275 r/min 时，破碎率最小，说明在进料量一定的情况下，滚筒转速过慢，将使花生荚果在脱壳仓内不能及时被揉搓脱壳而产生积压，脱壳滚筒的持续转动将导致破碎加剧；而过快的脱壳滚筒转速可增加对花生荚果揉搓，也将致使脱壳破碎率增大。滚筒转速与脱净率呈线性关系，且滚筒转速越高，滚筒对花生荚果的揉搓频次越高，进而使花生的脱净率提高。

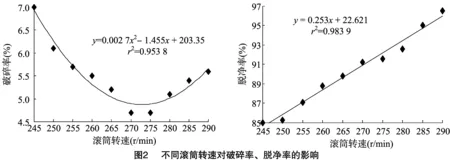
3.1.2 不同滚筒凹板筛间隙对脱壳质量影响 通过变频调节将滚筒转速设置为270 r/min，进料量继续保持在200 g/s，调节滚筒部件螺栓，以改变滚筒凹板筛间距D，研究不同滚筒凹板筛间隙对脱壳质量的影响。在滚筒凹板筛间隙分别为17、19、21、23、25、27、29、31、33、35 mm的条件下，开展滚筒凹板筛间隙的单因素试验。由图3可知，破碎率随滚筒凹板筛间隙的增大而逐渐减小，主要是因为滚筒凹板筛间隙过小时，导致脱出的花生不能及时排出而直接与旋转的滚筒再次作用产生破碎。脱净率随滚筒凹板筛间隙的增大而逐渐减小，说明在凹板筛间隙较大时，滚筒凹板筛之间填充的花生较多，随滚筒的转动花生之间相互挤压，而非滚筒直接作用于花生，致使花生脱净率下降。

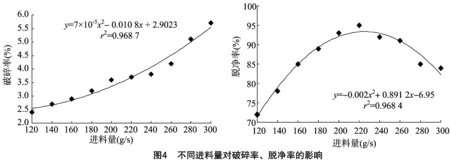
3.1.3 不同进料量对脱壳质量影响 将脱壳滚筒转速设置为270 r/min，滚筒凹板筛间隙设置为25 mm，通过调节花生脱壳试验台振动给料器来改变花生脱壳设备的进料量，研究不同进料量对脱壳质量的影响。在喂料量分别为120、140、160、180、200、220、240、260、280、300 g/s的条件下，开展进料量的单因素试验研究。由图4可知，破碎率随进料量的增大而逐渐增加，主要因为在其他条件不变的情况下，进料量增大致使滚筒凹板筛筛分能力不足，脱出物料不能及时排出而产生不必要的揉搓，从而导致破碎。脱净率随进料量的增加呈先升后降的趋势，主要因为进料量过大或者过小都不能使脱壳仓填充均匀，填充过少导致不能产生揉搓作用而脱不净；填充过多导致荚果之间相互揉搓作用增加而与滚筒揉搓几率减少，进而导致脱净率下降。

3.2 组合设计实验

按照中心组合试验设计方案，随机组合试验次序，所得试验设计及相关结果如表3所示[8]。

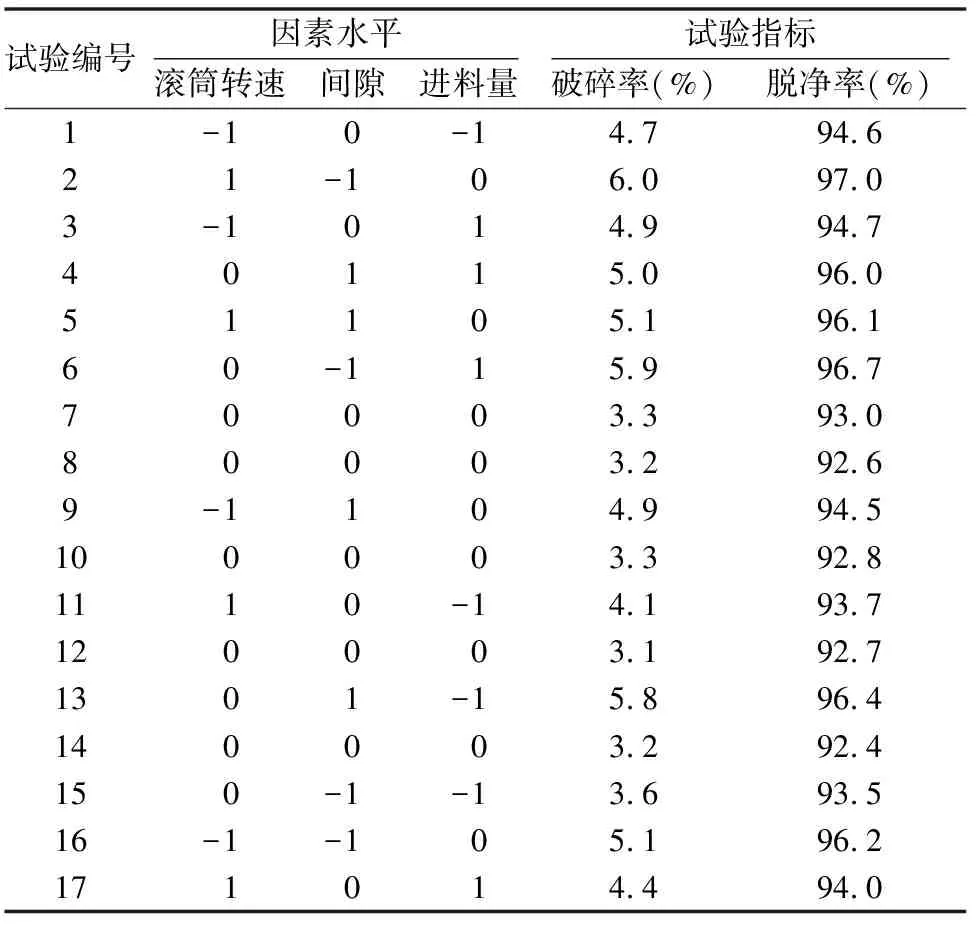
表3 中心组合试验设计方案及相应结果

3.2.1 破碎率数学模型及方差分析 采用逐步回归法对表3结果进行三元二次回归拟合并进行方差分析，得到的破碎率编码值简化回归数学模型为：

R1=3.22+0.025B+0.25C-0.18AB+0.025AC-0.78BC+0.75A2+1.30B2+0.55C2。

(3)

由表4可知，该破碎率数学模型显著性检验F=27.84，模型P值极显著，失拟项不显著，模型的修正决定系数R2=0.967 8，说明该回归数学模型与实际结果拟合精度高，可对脱壳设备的破碎率进行分析预测。该模型预测破碎率与滚筒转速、滚筒凹板筛间隙、进料量存在二次非线性相关关系。模型方差分析亦表明，滚筒凹板筛间隙与进料量间的交互作用对破碎率的影响较显著。

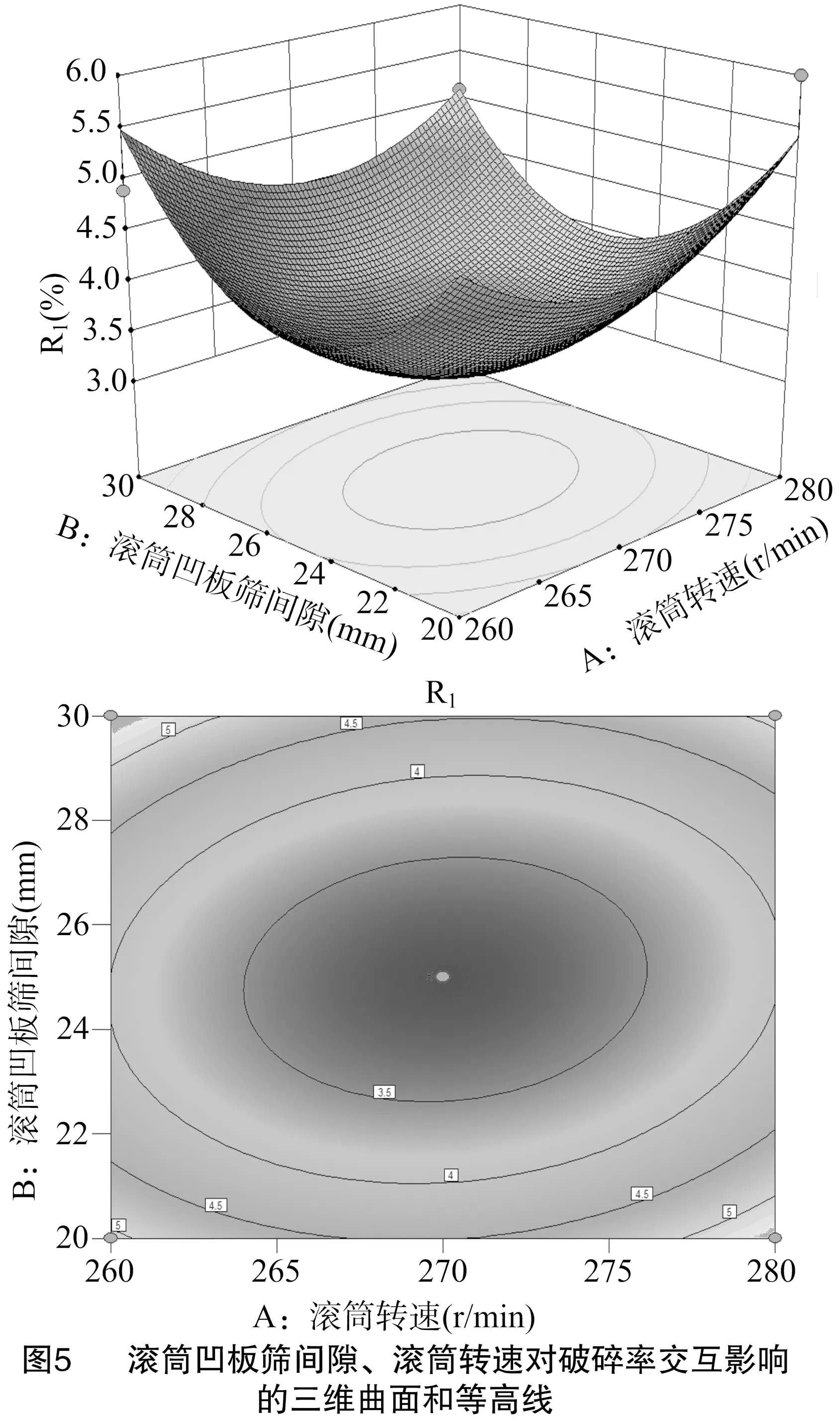
3.2.2 破碎率的响应曲面分析 根据表3试验数据，各因素对破碎率的响应面分析如图5至图7所示；根据图中三维曲面和等高线考察滚筒转速、滚筒凹板筛间隙、进料量对破碎率的影响，分析结果见图5至图7，根据等高线形状判断交互作用强弱[9-11]。由图5至图7中的等高线可以看出，滚筒转速和滚筒凹板筛间隙、滚筒凹板筛间隙和进料量、滚筒转速和进料量的交互作用显著。由图5可以看出，滚筒转速和滚筒凹板筛间隙交互作用对破碎率影响较为显著。由图6可以看出，当滚筒转速一定时，降低进料量可以降低破碎率。由图7可以看出，当滚筒凹板筛间隙一定时，增加进料量破碎率先减小后增大。

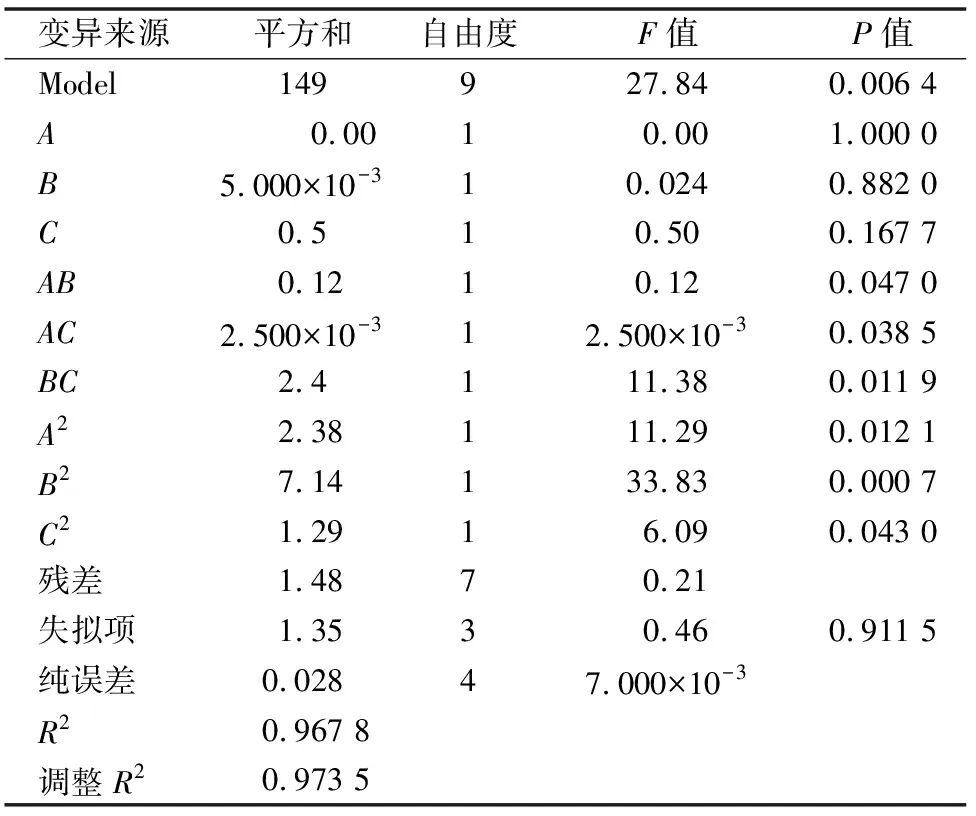
表4 破碎率数学模型的方差分析

注：P<0.01为极显著；P<0.05为显著。表5同。

3.2.3 脱净率的数学模型及方差分析 对表3进行三元二次回归拟合及方差分析，得到的脱净率编码值简化回归数学模型为：

R2=92.70+0.10A-0.05B+0.40C+0.200AB+0.052AC-0.900BC+0.92A2+2.32B2+0.63C2

由表5可知，该脱净率数学模型显著性检验F=46.800，模型P值显著，失拟项不显著，模型的修正决定系数R2=0.976 1，说明该回归数学模型与实际结果拟合精度高，可对脱壳设备的脱净率进行分析预测。通过该预测模型可以看出，滚筒转速、滚筒凹板筛间隙、进料量与脱净率存在二次非线性相关关系。方差分析可以看出，脱壳滚筒转速与滚筒凹板筛间隙、滚筒凹板筛间隙与进料量的交互作用对脱净率影响显著。

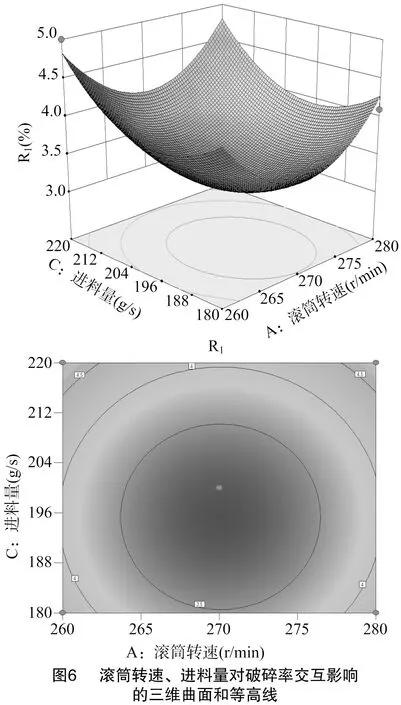
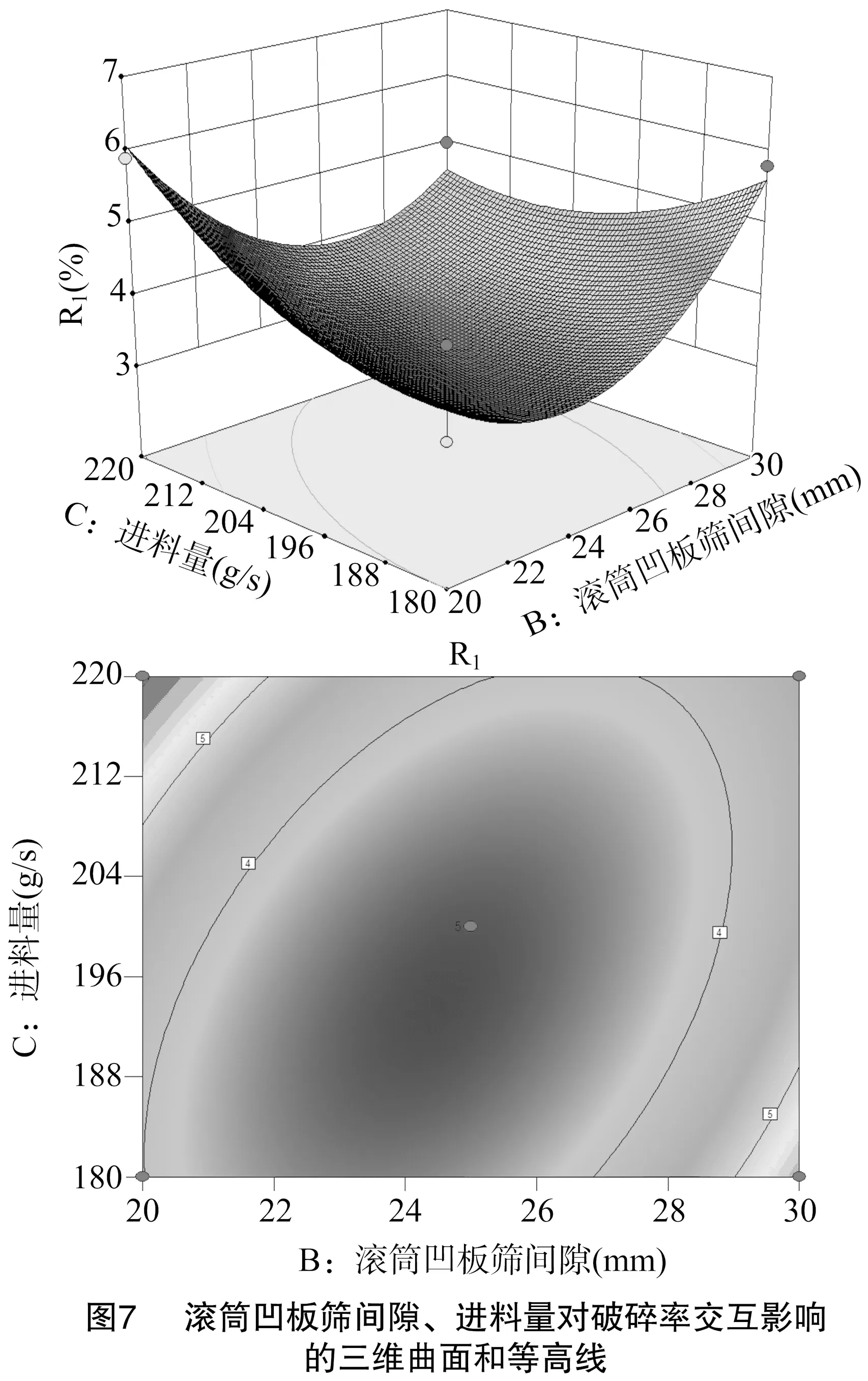
表5 脱净率数学模型的方差分析

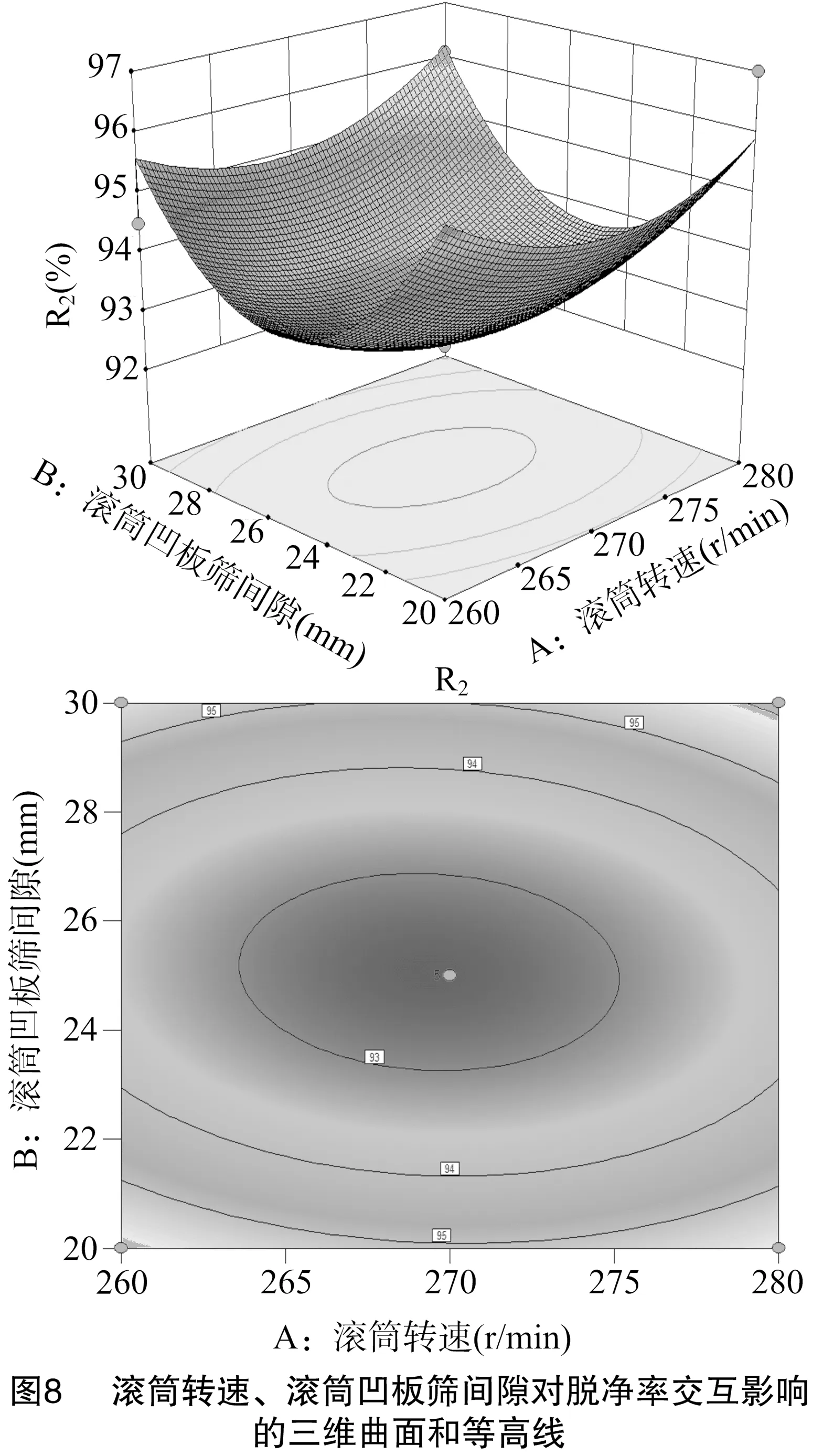
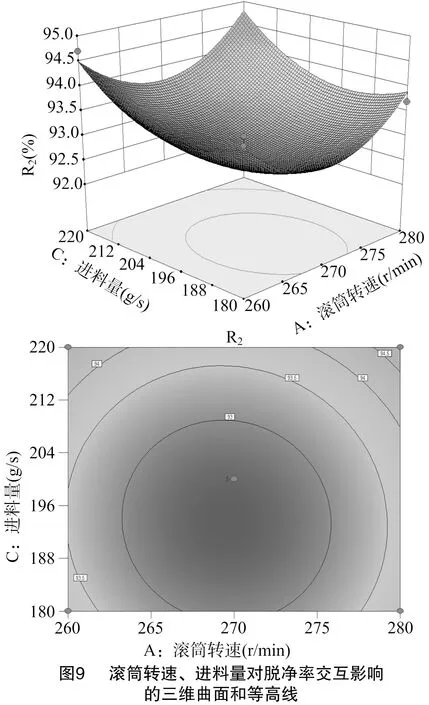
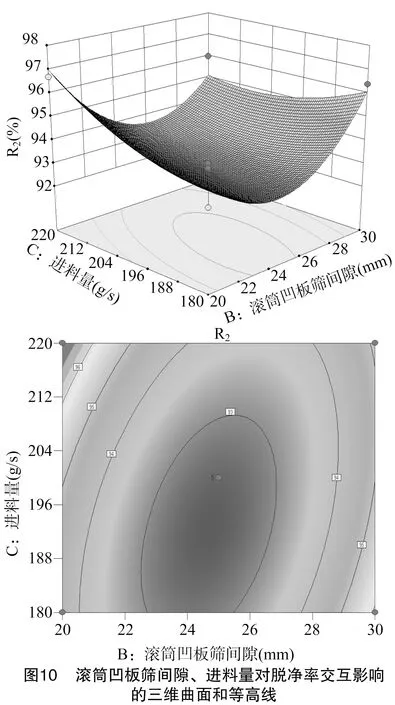
3.2.4 脱净率的响应曲面分析 由图8至图10可以看出，滚筒转速和滚筒凹板筛间隙、进料量和滚筒凹板筛间隙的交互作用对脱净率影响明显，其他交互作用影响不显著。由图8可以看出，当滚筒凹板筛间隙一定时，提高滚筒转速，脱净率先减小后增大。由图9可以看出，当滚筒转速一定时，脱净率随进料量的减小而逐渐减小。由图10可以看出，当滚筒凹板筛间隙一定时，脱净率随进料量的减小而逐渐减小。

4 参数优化

从脱壳机的实际工作质量考虑，需同时考虑响应值R1、R2，使R1的响应值达到最小，R2的响应值达到最大。为此本试验对2个目标函数进行多目标优化，以探明满足2个目标函数的最佳参数组合：

由于破碎率和脱净率同等重要，因此在优化过程中将2者的重要程度均设置为5[12-13]。采用design expert进行优化分析可得出，当脱壳滚筒转速为274.8 r/min，滚筒凹板筛间隙为24.7 mm，进料量为204.6 g/s时可得破碎率、脱净率最佳值，分别为3.2%、94.6%。

5 验证试验

为验证试验结果的可信度，将脱壳试验台参数设置为脱壳滚筒转速275 r/min、滚筒凹板筛间隙25 mm、进料量 205 g/s，开展花生脱壳破碎率、脱净率的验证试验，试验重复3次，结果如表6所示。

由表6可知，破碎率相对误差为6.9%，脱净率相对误差为1.5%，与优化结果理论值相差较小，进一步验证了试验结果的可信度及试验方案的可行性。

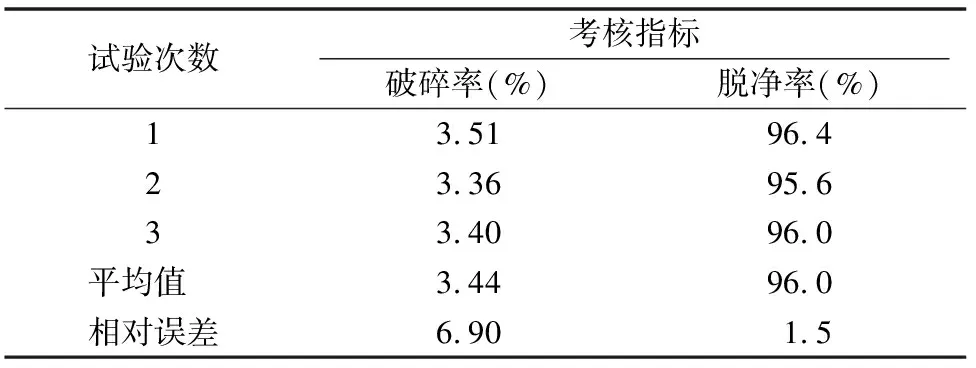
表6 验证试验结果

6 讨论

本研究通过单因素试验和响应曲面法进行试验机结果分析，建立花生脱壳机脱壳破碎率及脱净率的数学模型，采用响应曲面分析方法判断脱壳滚筒转速、滚筒凹板筛间隙、进料量以及各因素交互作用与破碎率及损失率关系。

以破碎率最小、脱净率最大为主控目标，对试验结果进行分析优化得到，花生脱壳机关键参数的最优值为脱壳滚筒转速274.8 r/min、滚筒凹板筛间隙24.7 mm、进料量204.6 g/s，并在此参数下开展试验验证，结果表明，脱壳设备在该参数下的破碎率为3.44%、脱净率为96.0%。