图(n≤9)的优美性*

魏众德，李敬文，武永兰

(兰州交通大学电子与信息工程学院，甘肃 兰州 730070)

现实世界中大多数问题可以抽象为图论问题，即事物或现象代表为点，事物之间以及现象之间的某种联系抽象为边，用图表示出事物之间联系的拓扑结构，进一步转变为对图的研究。图论的起源可以追溯至1736年EULER对格尼斯堡七桥问题的研究，但在随后的近200年里发展缓慢。受近代电子计算机发展的影响，图论在近年来得到快速发展，形成了一个重要的数学分支，并与矩阵论、群论等分支相互交叉做研究。图论广泛应用于计算机科学、网络、有机化学等多个领域，尤为热门的机器学习、神经网络，以图论的数学理论背景作为基础，进而研究出基于图论的机器学习算法，并得以广泛应用。

图的优美标号问题是图论中最为热门的研究之一，它的研究始于20世纪60年代Rosa[1]提出的优美树猜想：所有的树都是优美的，由于优美标号的组合数变化很多，在数学理论分析上造成很大困难，因此该猜想至今无人证明或否定，2010年Fang等[2]利用计算机算法证明了35个顶点内的所有树都是优美的。在优美树猜想提出的近40年中，又有多人提出了其它相关猜想，比如：1980年Graham等[3]提出：任何树都有和谐标号，1991年Gnanajothi等[4]提出：每棵树都是奇优美的。标号种类以及标号理论分析的多样性使得研究者查阅文献较为困难，而在文献[5]中，则详细列出了近60年内所有标号的研究现状。优美图的概念由Rosa[1]首次提出，随后Golomb[6]对优美图给出了明确的定义。由于优美图在军事方面比如：雷达脉冲码，通信网络等方面的广泛应用，所以更加引起学者们的重视，并且其理论研究具有重要价值。

国内外学者对优美图的研究，目前主要集中在树、与圈相关的图、部分特殊图、并图和一些非连通图等方面[7-10]，例如毛毛虫、花树等特殊树目前已经证明是优美的。而对于一般图的优美性及非优美性研究很少，Erdös[3]在未正式发表的一篇论文中阐述了多数图并不是优美的，但未得到证明。Rosa认为一个图G是非优美的主要有3个原因[1]：① 图G有太多的顶点且没有足够的边；②G有太多的边而没有足够的顶点，③G的边数具有错误的奇偶性。因此，本论文结合文献[11]给出的生成非同构图的算法源代码，以及结合目前已实现的优美标号算法，给出了9个点内的所有优美图及非优美图的数量，并对数据进行分析，得出该范围内的所有图，非优美图占比很小，且非优美图的分布很有规律，大致满足Rosa提出的3个基本原因；对应的，优美图的分布也呈现出很有趣的现象，下节给出具体定理和相关猜想。

文中所用的[m,n]为集合{m,m+1,m+2, …,n}，即从m到n的自然数。为方便起见，

以下给出优美标号和优美图的定义。

定义1[6]如果一个(p,q)图G(p个顶点，q条边)存在一个映射f:V(G)→[0,q],使得图G中任意两个顶点x、y满足f(x)≠f(y),并且定义边uv∈V(G)的标号为f(uv)=|f(u)-f(v)|。当{f(uv):uv∈E(G)}=[1,q]时，则称f为图G的一个优美标号(garceful labeling)，图G称为优美图(graceful grpah)。

算法是基于搜索优美空间的，进而找出图的优美标号。为了详细说明算法的执行过程，以下给出优美空间的明确定义。

定义2 对于边数为q的一类优美图，都存在一个表(如表1)，并且满足：

(i) Min(f(u),f(v))≥0；

(ii) Max(f(u),f(v))≤edgeLabel；

(iii) |f(u)-f(v)|=edgeLabel。

则称此表为边数为q的优美集合，又称q优美空间。

表1 q优美空间Table 1 q graceful space

由此可知，对于每个边标号(edgeLabel)，对应的取唯一一个二元组(由该边的两个相邻顶点标号组成)，而这些二元组集合组成的图都是优美的。

例1 如表2为q=9的优美空间，取出的二元组对应优美图如图1所示。

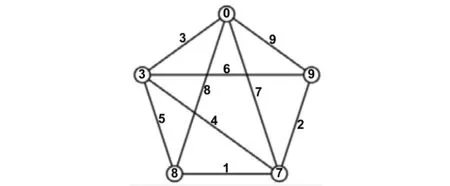
图1 G(5,9)优美标号Fig.1 A graceful labeling of G(5,9)

表2 q=9优美空间Table 2 Graceful space with q=9

文中是对9个点内的所有图进行了优美性验证，其中包含了树、单圈图、双圈图以及其它图，而树和单圈图已经提出相关猜想，以下列出：

猜想1[1]所有的树都是优美的。

猜想2[12]除了圈Cn,n(mod 4)={1,2}是非优美图之外，其它所有的单圈图都是优美的。

1 定理和猜想

本文所讨论的图均为简单连通图，若为非连通图则另加说明。对于一类(p,q)图，判断其中每个图是否优美的解决思路如下：①q优美空间可以组合出q!个图；②q!个图中包含非连通图和连通图，但都是优美的；③ 所有(p,q)图中的优美图都包含在q!个图中，即q优美空间具有完备性；④ 如果一个(p,q)图不包含在q!个图中，则它是非优美的。基于以上4个思路设计的优美图判定算法，可知，算法具有正确性，第二节将给出算法详细步骤。根据算法实验结果，给出如下定理和猜想。

一类(p,q)图，在边密度过大的情况下，会导致这一类(p,q)图中的所有图全部非优美。以下给出定理1，在9个点范围内，(p,q)图由完全图再减去m条边(Kn-m)，这类(p,q)图仍然是非优美的。

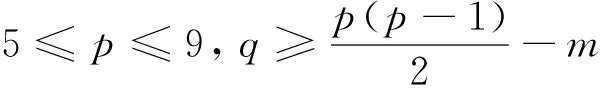
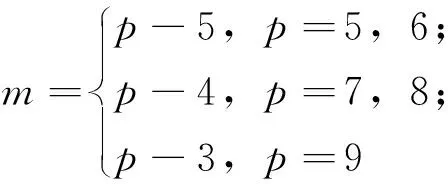
由定理1，可得如下猜测，对于(p,q)图，当点数大于9时，边数在一定范围内，这类(p,q)图都是非优美的。

猜想3 当

时，图(p,q)是非优美的,其中m=0, 1, … ,p-3。

算法搜索结果得知，在9个点范围内，部分(p,q)图中的所有图全部是优美的。

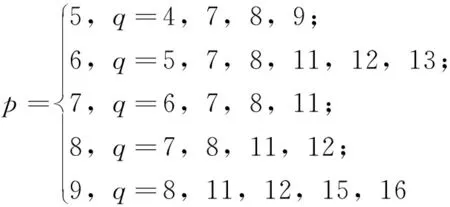
在9个点范围内，并且边密度不大的情况下，(p,q)图呈现出一定的规律性：当q(mod 4)={0,3}时，这类(p,q)图中的非优美图占总图的比例很小，可以认为绝大多数图都是优美的，根据实验结果，对“边密度不大”量化为q≤[3.7p-9.3]，因此可得定理3。

定理3 当5≤p≤9，q≤[3.7p-9.3]，且q(mod 4)={0,3}时，几乎所有的(p,q)图是优美的。

证明由表3-表7可知，在边密度不大的条件下，边数q呈现出一定的规律性，即q(mod 4)={0,3}时，(p,q)图中几乎所有的图都是优美的，根据表中数据对此条件进行量化，取出散点(x,y),其中当p=x,q≤y时，(p,q)图满足此规律，由表3-表7可分别取出散点(5,9)、(6,13)、 (7,17)、(8,20)、(9,24),如图2所示。

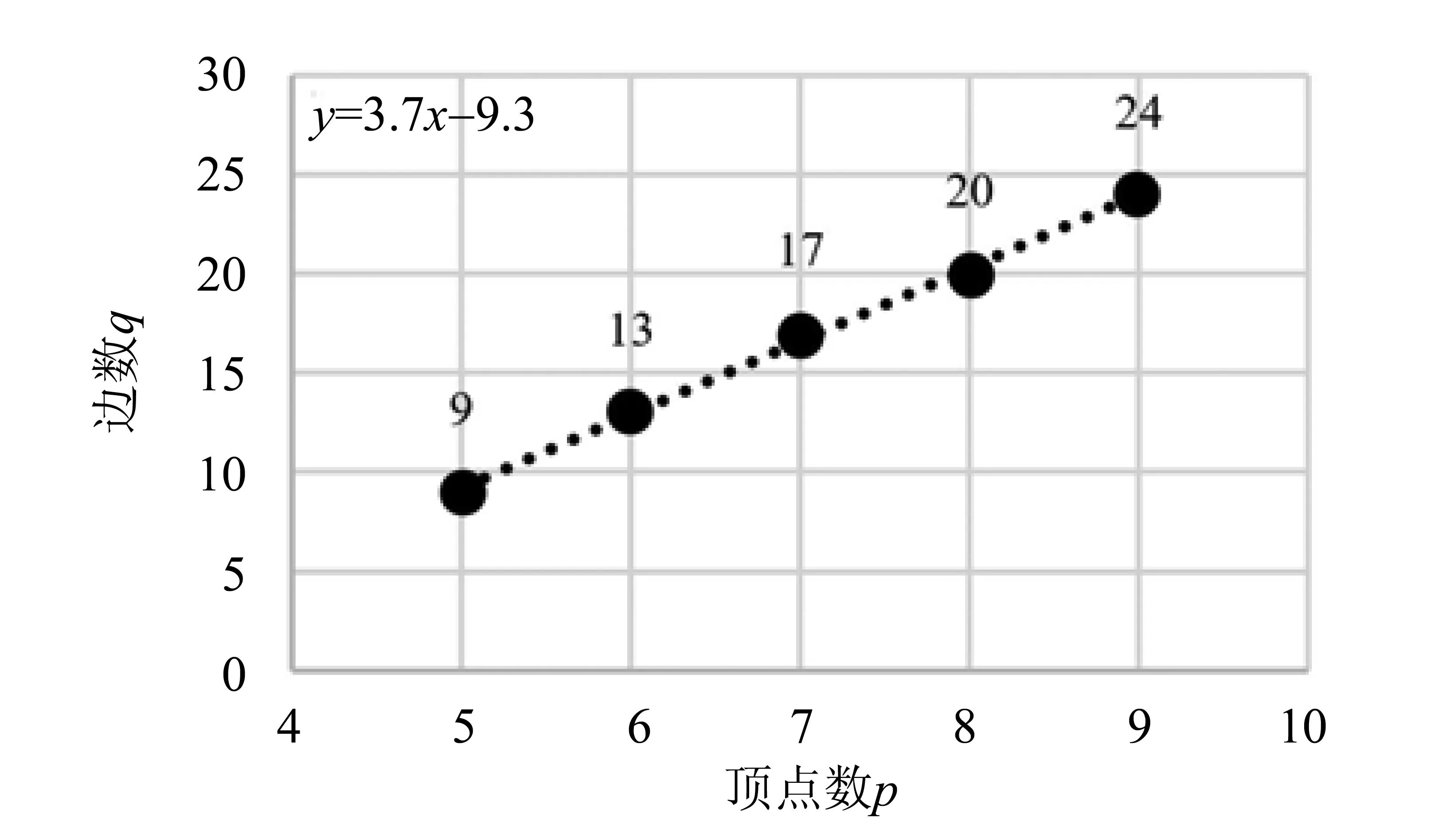
图2 9个点内“边密度不大”上界Fig.2 The upper boundary of “small side density” in the 9 points

对数据进行线性拟合，可得y=3.7x-9.3，由于边数为整数，故定义y=[3.7p-9.3]。因此，q≤[3.7p-9.3]，定理3成立。

由定理3，可以进行如下猜测，当点数大于9时，该规律依然满足。

猜想4 当p>9,q≤[3.7p-9.3], 且q(mod 4)={0,3}时，几乎所有的图(p,q)是优美的。

由于9个点内“边密度不大”的上界是根据实验数据结果限定的，本质上是一个模糊界限，但是可以对图论中相关标号领域的研究给予数据支持。

2 优美图判定算法

首先利用文献[11]中的生成非同构图算法，生成9个点内的所有非同构图，并且按不同的点与边进行区分，以邻接矩阵形式分别存储于文件p_q.txt中。

本算法包含2个子算法，分别为：基于优美空间搜索判定算法和基于邻接矩阵优美判定算法。算法1的基本思想是：首先对文件p_q.txt做预处理，其中p为图的顶点数，q为对应边数，预处理包括4部分：(i)计算文件中图的总个数；(ii)求每个图对应的度序列；(iii)求每个图对应的特征值；(iv)对每个图设一个标志，用于标识该图是否已经优美；然后搜索优美空间，搜索出的图与源文件中的图进行对比，如果为文件中第i个图，则将图Gi标为优美。

算法1 基于优美空间搜索判定算法

输入: (p,q)图的邻接矩阵文件p_q.txt

输出: 文件中所有非优美图

1.begin

2.读邻接矩阵文件p_q.txt

3.fori1→nn是文件中所有图的总个数

4.ComputeDegreeSeq(Graphi)

5.ComputeEigenvalue(Graphi)

6.IsGraphiGrace=false

7.end for

8.search graceful space

9.二元组集合→邻接矩阵TempMatrix

10.ComputeDegreeSeq(TempMatrix)

11.ComputeEigenvalue(TempMatrix)

12.fori1→n

13.if(IsDegreeSeqSame(Graphi,TempGraph)&&IsEvalueSame(Graphi,TempGraph)

14.IsGraphiGrace=true;

15.break;

16.end for

17.if(eachGraph is graceful)

18.break;

19.end search

20.fori1→n

21.if(IsGraphiGrace==false)

22.output(Graphi);

23.return

24.end

考虑到优美空间庞大以及搜索整个优美空间的时间复杂度较高，当文件中所有图都已经标为优美时，或者该文件中大部分图都已标为优美，只有少量暂时未标为优美的图时，算法1可以结束，用算法2解决剩余图。算法2的基本思想是：对于给定的图，对应图的邻接矩阵为Mn，其中Mij=1代表顶点i与顶点j之间有边(i≠j)，对Mii进行优美标号，Mii即代表该图中的各个点，标号过程为：首先从优美空间中选出边标号为q的1个二元组，然后将二元组(m,n)中的2个值分别标于邻接矩阵的主对角线上，即Mii=m，Mjj=n，并且需要满足条件Mij=1，然后选出边标号为q-1的1个二元组(m′,n′)，标于邻接矩阵主对角线上，边标号递减，如果当前边标号无法在邻接矩阵中标成功，则回退至上一级，重新开始标号；如果边为1的1个二元组已经标成功，则说明该图是优美的，算法结束。如果整个优美空间已经搜索完毕，仍未找到该图的优美标号，则确定该图是非优美的。算法2的具体步骤如下：

算法2: 基于邻接矩阵优美判定算法

输入: 一个邻接矩阵Mn

输出: 该邻接矩阵对应图是否优美

1.begin

2.search graceful space(edgeLabel)edgeLabel∈{0,1,2,…,q}

初始化edgeLabel=q

3.if(edgeLabel==0)

4.this graph is graceful;

5.return;

6.select a two tuple(m,n)

m∈{0, 1, …, edgeLabel-m},

n∈{edgeLabel, edgeLabel+1, …,q}, |n-m|=edgeLabel.

7.If (tuple(m,n) is not enabled)

8.ReSelect tuple;

9.fori1→n

10.If (Miiis enabled)

11.Mii=m;

12.forji→n

13.If (Mjjis enabled&&Mij==1)

14.Mjj=n;Mij=edgelabel;

15.end forji→n

16.end fori1→n

17.If (conflict-free)

18.search graceful space(edgeLabel-1)

19.end search

20.if (grace space search finished)

21.This graph is ungraceful

22.end

由于算法2针对一个特定图，相比算法1的盲目搜索而言，算法2具有更好的收敛性，且往往是计算机验证非优美图的有力工具。

3 算法结果与分析

本文利用上述优美性判定算法，结合文献[11]中给出的生成非同构图算法，对9个点内的所有图进行了优美性验证，以下分别列出对9个点内的所有图的优美个数统计表，以及各个点之间图的优美及非优美数对比表，由于篇幅有限，本文只给出部分非优美图和优美图。

算法运行环境及硬件配置如下：

操作系统：Windows 764位

处理器：Intel(R) Core(TM) i7-7700 CPU@3.60 GHz

RAM: 64.0 GB

开发环境：Visio Studio 2013

开发语言：C#

3.1 点数为2-9的所有图优美个数统计

程序运行结果表明，当点数为2,3,4时，对应的所有图是优美的，图的总个数分别为1,2,6。以下列出当点数为5-9时所有图的优美数及非优美数，如表3-表7。第1列为(p,q)，p为图的点数，q为图的边数，可知，当点数为p时，q范围为[p-1,p(p-1)/2]；当q=p-1时，此时图全部为树，当q=p(p-1)/2时，此时图为完全图；第4列为当点数为p，边数为q的情况下图的总个数；第2列与第3列分别为当前图集中优美图个数与非优美个数。

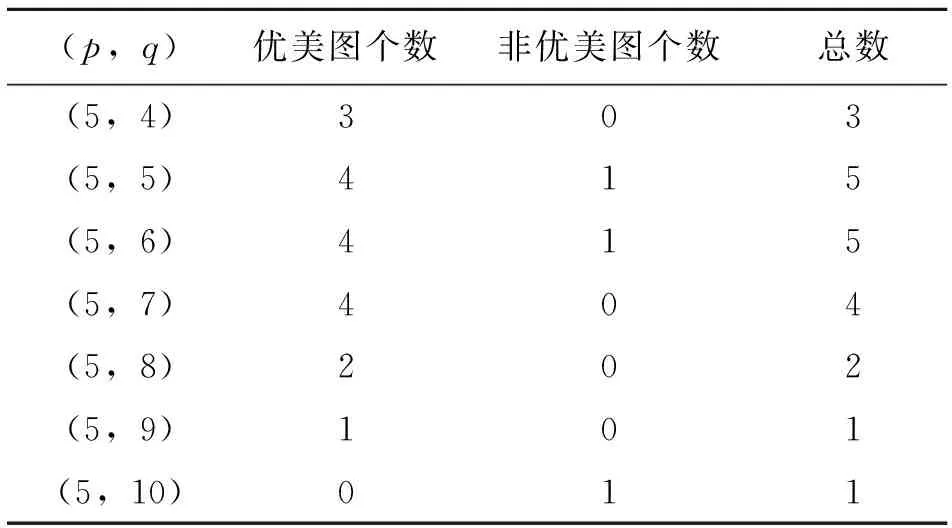
表3 点数为5Table 3 The number of vertices is 5

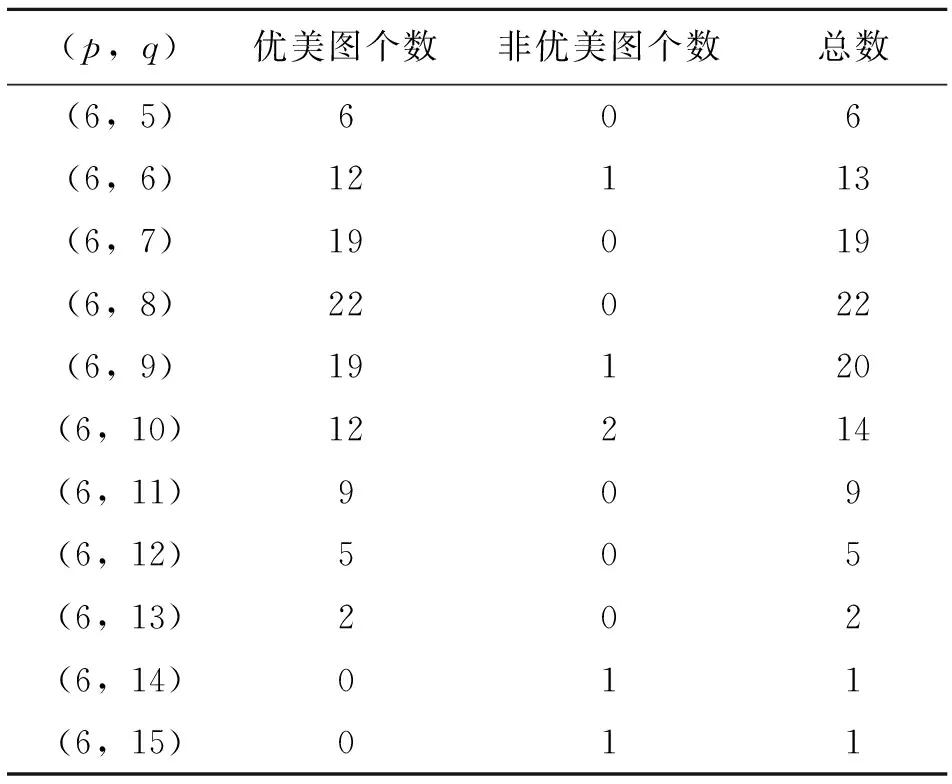
表4 点数为6 Table 4 The number of vertices is 6

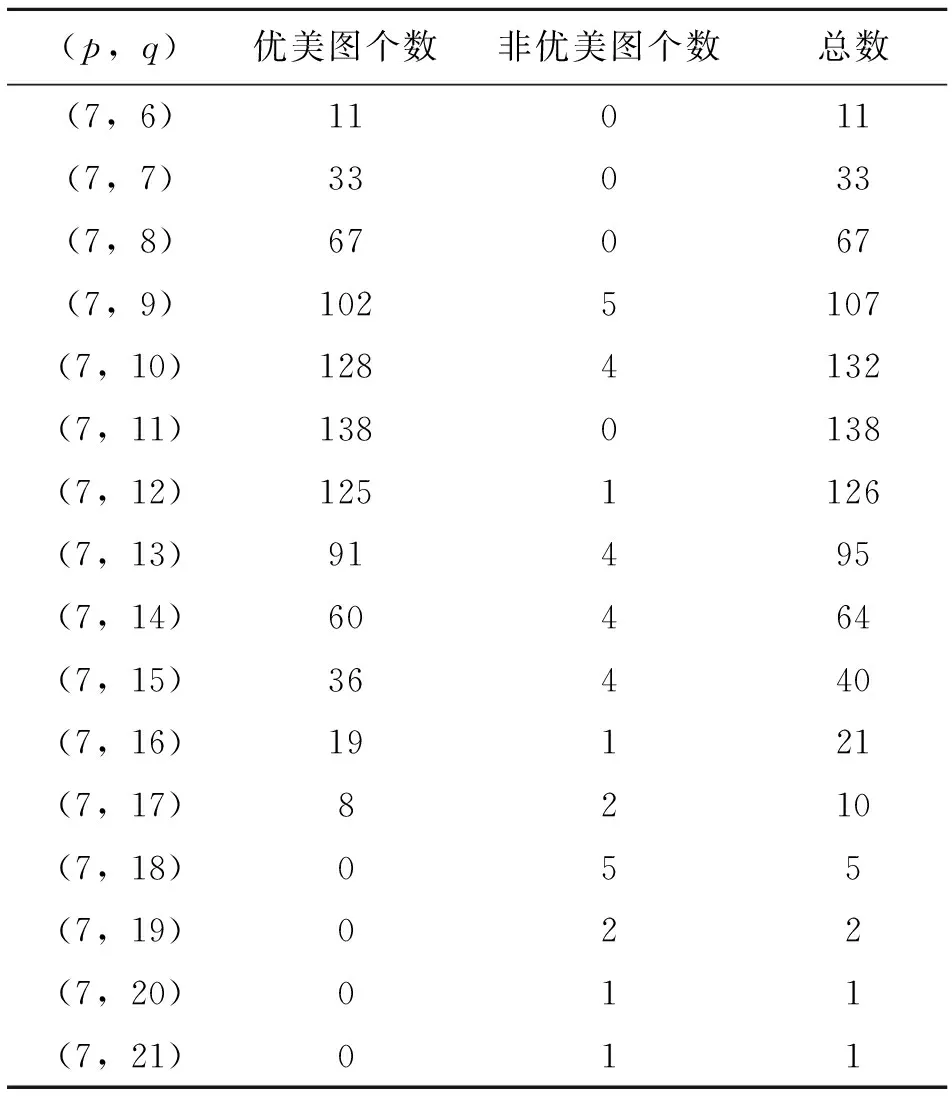
表5 点数为7Table 5 The number of vertices is 7

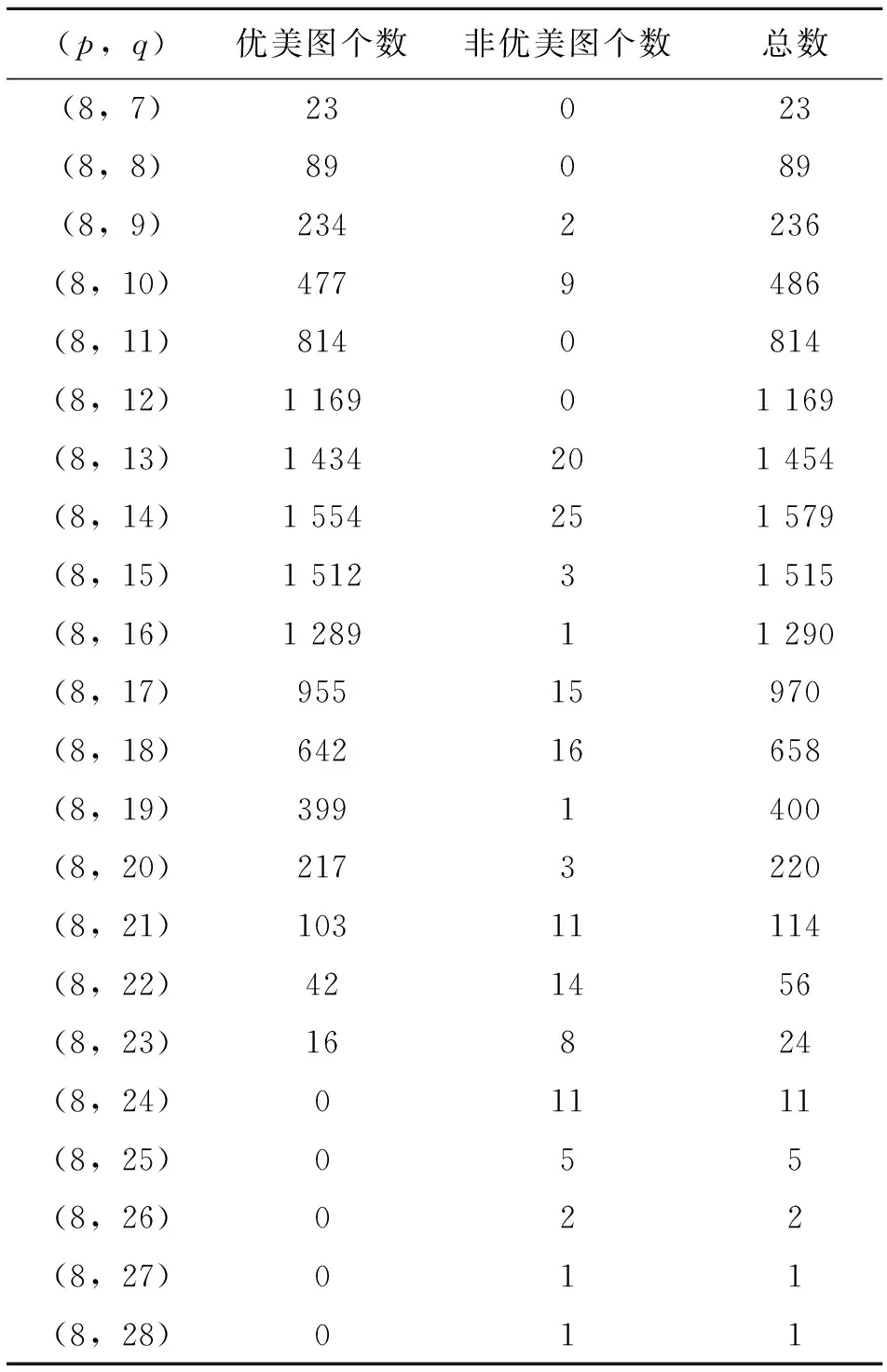
表6 点数为8Table 6 The number of vertices is 8

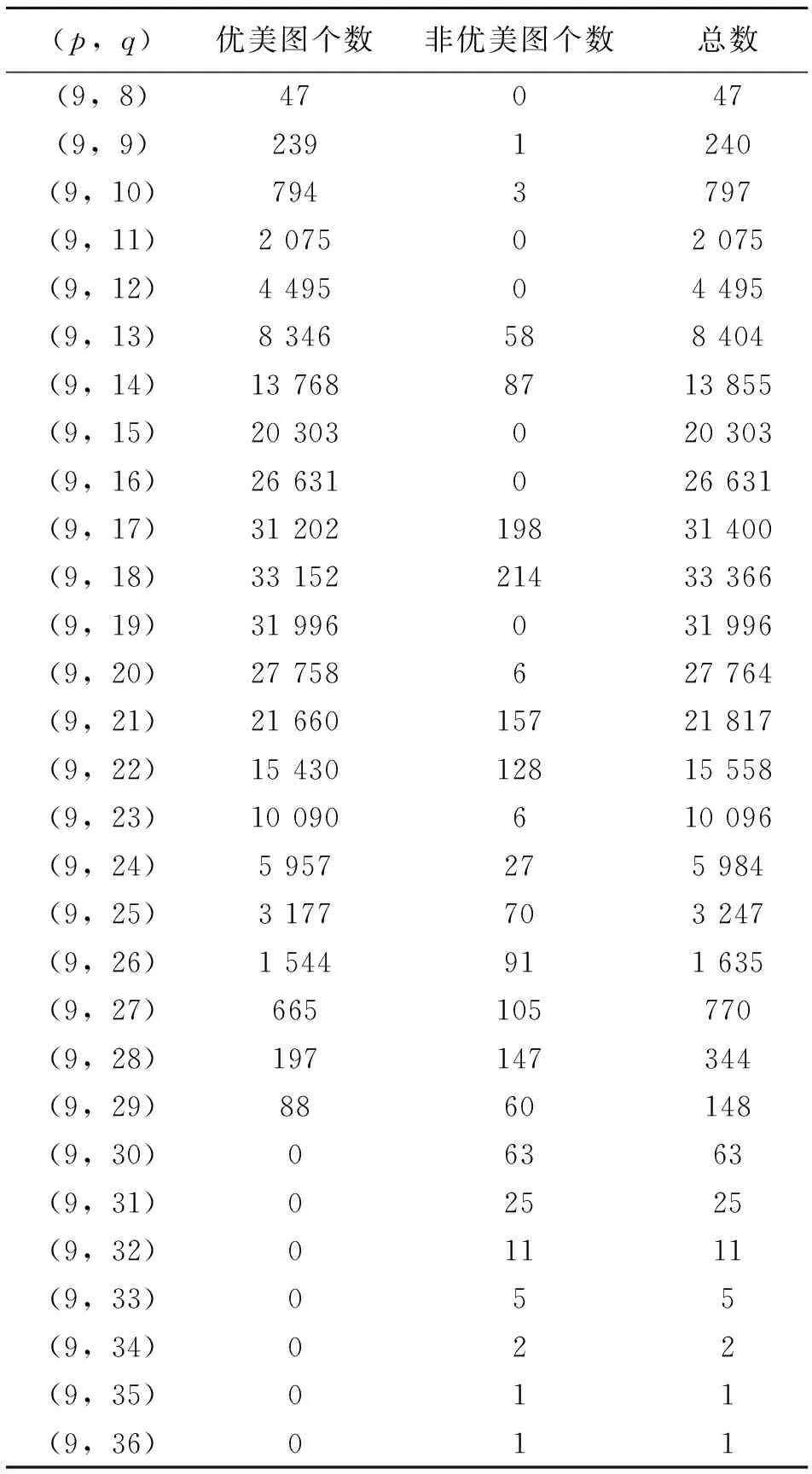
表7 点数为9Table 7 The number of vertices is 9

由表3-表7可以看出，(5,10)，(6,14-15)，(7,18-21)，(8,24-28)，(9,30-36)中的所有图都是非优美的，符合Rosa提出导致一个图非优美的基本原因中的第2条，由此可得定理1，并提出猜想3；由表6和表7可知，在边数不过大的情况下，当q(mod 4)=1,2时，其非优美图个数占当前图总数的比例大幅增加，而当q(mod 4)=0,3时，其非优美图个数占比又相对很小，符合Rosa提出导致一个图非优美的基本原因中的第3条，即G的边数具有错误的奇偶性，由此可得定理2、定理3，并提出猜想4。尽管非优美图较多，但相比图的总数而言，非优美图的数量还是很少的，如表8所示，列出了2-9个点内所有图的优美数量和非优美数量以及非优美占比。

由表8可知，当p≥5时，有非优美图出现，但是非优美图数量占图总数的比例很小，而且比率呈现减小趋势，因此可以得出，9个点内大部分图都是优美的。

3.2 9个点内部分非优美图

以下给出9个点内的部分非优美图，非优美图的命名规则如下：G(p,q,num)，其中p为点数，q为边数，num表示当前(p,q)图下的第几个非优美图，如果(p,q)图中的非优美图只列出1个，则该图直接命名为G(p,q)。

点数为5的非优美图已经由文献给出，一共有3个，如图3所示。

点数为6的非优美图一共有6个，如图4所示，其中(1)为圈C6，文献[1]已经给出对于圈图的优美性证明，(6)为完全图K6，文献[6]已经证明了当n≥5时，Kn是非优美的。

点数为7的部分非优美图如图5所示，其中(3)为荷兰风车，文献[13-14]中已经得出相关结论。

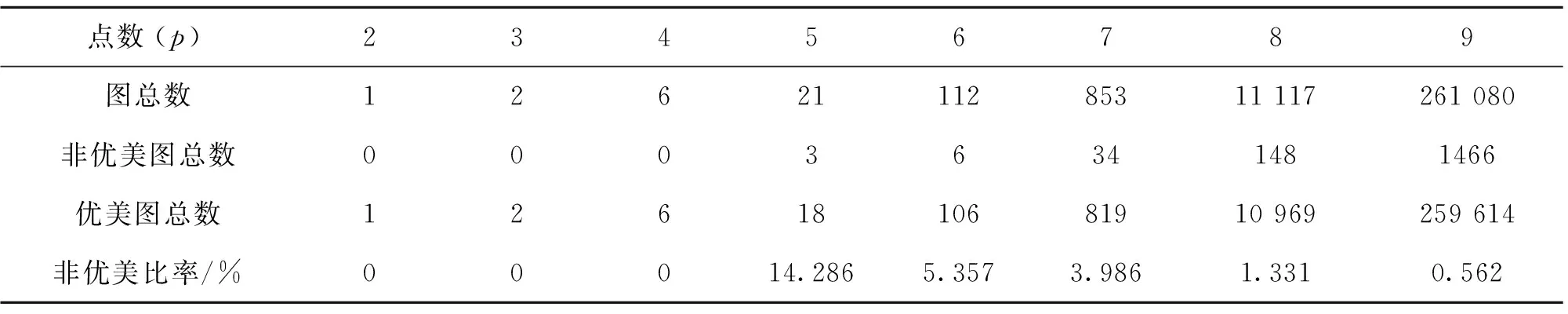
表8 2-9个点内所有图的优美个数对比Table 8 A comparison of the number of graceful numbers of all graphs in 2-9 points

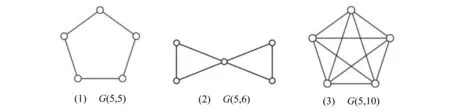
图3 p=5的非优美图Fig.3 Ungraceful graphs with p=5

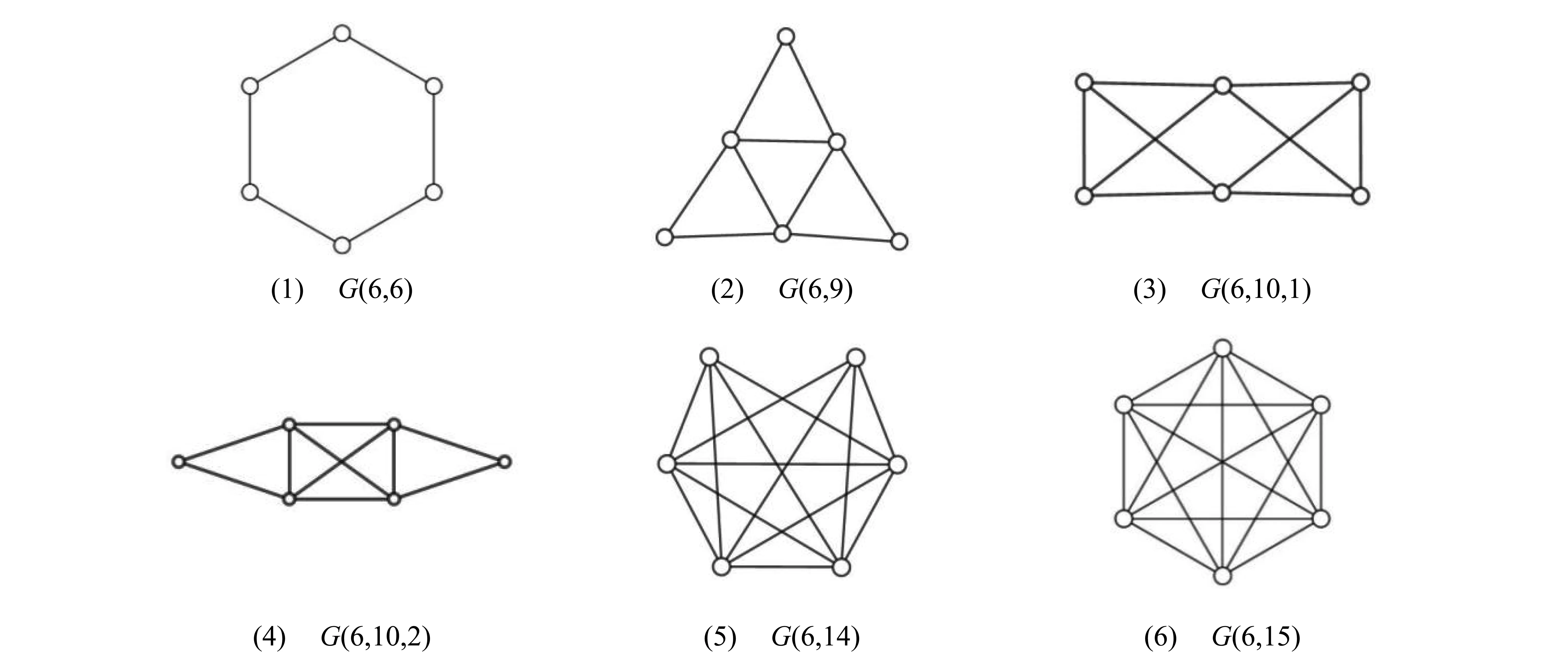
图4 p=6的非优美图Fig.4 Ungraceful graphs with p=6

点数为8的部分非优美图如图6所示。

点数为9的部分非优美图如图7所示。其中(2)、(3)、(4)是有两个圈共用一个顶点形成，(8)为两个K5共用一个顶点形成。

由以上部分示例可以得出，大部分非优美图呈现出很强的对称性，且很多以并图的方式出现，并且其中有些图已经被数学证明是非优美的。

3.3 9个点内部分优美图

为了说明算法的正确性和真实性，以下列出9个点内部分优美图，而这些优美图的标号多数情况下手工方式较难给出，以(8,13)，(9,14)部分优美图为例。

(8,13)部分优美图如图8所示。

(9,14)部分优美图如图9所示。

图6 p=8的部分非优美图Fig.6 Partial ungraceful graphs with p=8

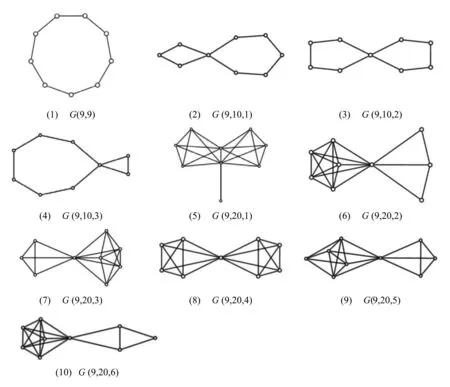
图7 p=9的部分非优美图Fig.7 Partial ungraceful graphs with p=9

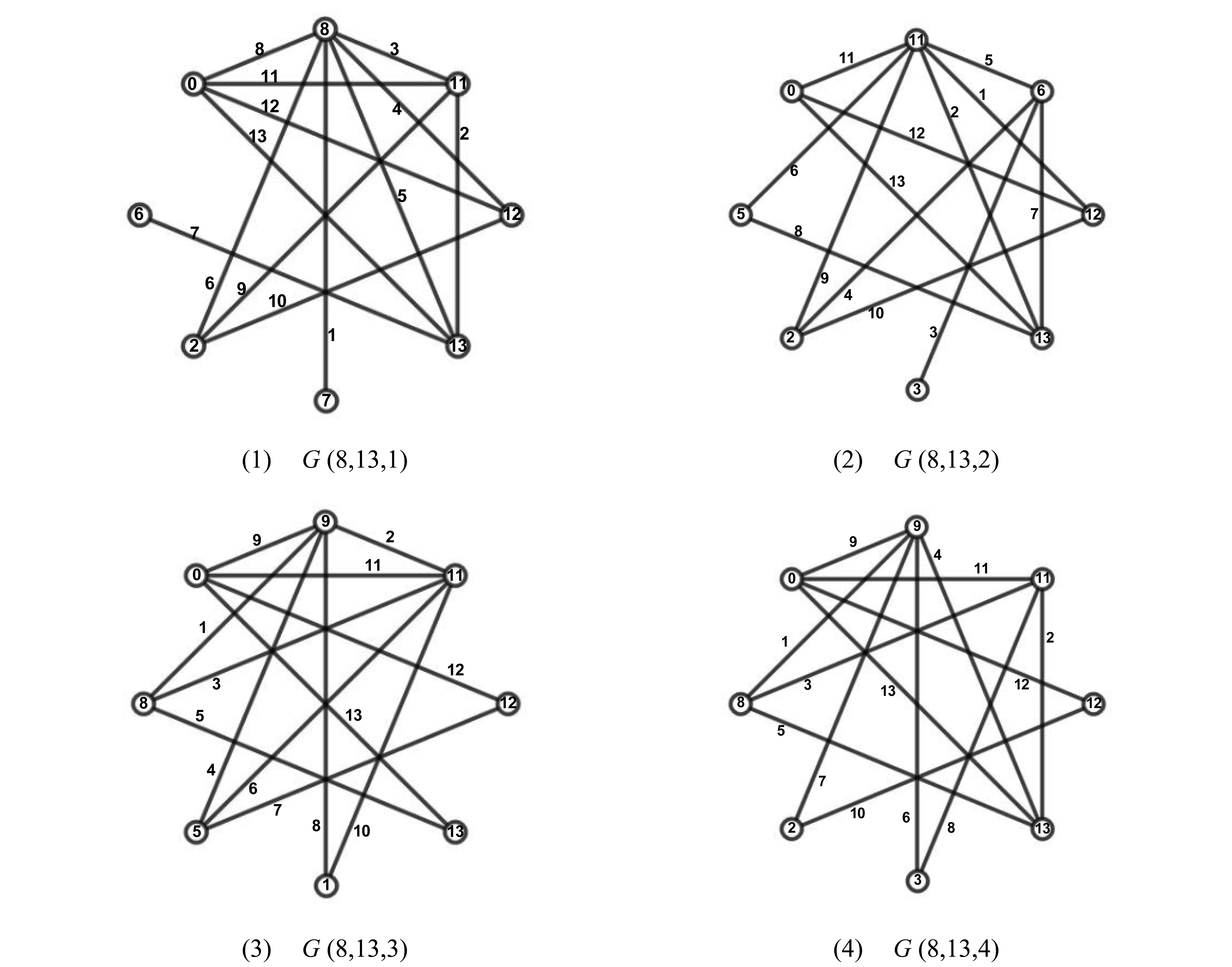
图8 (8,13)部分优美图Fig.8 Partial graceful graphs of (8,13)

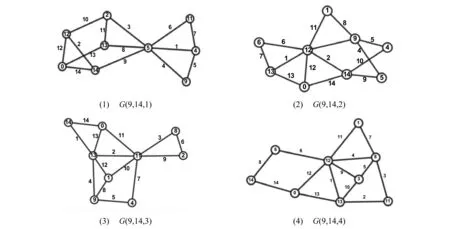
图9 (9,14)部分优美图Fig.9 Partial graceful graphs of (9,14)

随着点数增大以及边数增多，对应的优美空间也就越大，且图的总数量呈现出指数级增长，这导致存储空间过大以及算法执行效率下降。因此，本文只验证了9个点内所有图的优美性。

4 结 语

本文给出一种针对一般图的优美性验证算法，并引入预判函数对算法进行优化，该算法可以得出任意图的优美标号，或者确定该图非优美。然后利用该算法对9个点内的所有图进行优美性分析，最终得出该范围内所有的非优美图。结果表明，虽然非优美图数量较多，但相比总数而言，非优美图数量占比极小，而且呈现出很强的对称性，可以认为，在有限点内，绝大多数图是优美的。文中第四节给出相关数据及部分非优美图和优美图，对数据进行分析，得到了3个定理，并提出相关猜想，且所得到的数据可以为图标号领域内进一步证明相关猜想提供基础数据支持。

由表8可知，9个点内的所有图的总数为273 192，优美图总数为271 535，优美比率达到99.393 5%；另由定理2可知，部分点、边数确定的(p,q)图是全部优美的，因此，本文提出两个公开问题，如下：

问题1 Erdös提出大部分图是非优美的，但未得到明确的证明。本文实验得出9个点内大部分图是优美的，优美比率达到99.393 5%，且非优美比率呈递减趋势。那么随着点数的增加，非优美的比率会怎样变化？

问题2 当p、q满足一定的条件时，这类(p,q)图全部是优美的或者是非优美的，比如：(9,19)图中31 996个图全部是优美的，(8,24)中11个图全部是非优美的，这类图具有怎样的特性？该如何刻画？