基于事故树对炸药压装工艺爆炸事故的成因分析

赵 丹，何中其,胡毅亭

(南京理工大学化工学院，江苏 南京 210094)

炸药压装工艺是常用的炸药装药方法之一，不仅在军用而且在民用爆破器材的制备中都有广泛使用，如石油射孔弹、震源弹的扩爆装药、平炉射孔弹、工程爆破用的扩爆药柱等[1]。根据现场调研和以往事故案例分析发现，炸药压装工艺的爆炸事故率较高，因此对炸药压装工艺爆炸事故成因进行研究并提出相应的解决措施非常必要。

目前针对炸药压装工艺爆炸事故的原因分析主要集中在对以往事故案例的剖析上。如刘桂涛等[2]通过对两个工厂发生的炸药压装工艺爆炸事故的分析，得出了导致事故的直接原因，并提出了相应的安全技术措施；黄文斌等[3]运用模糊综合评价法对高能炸药分步压装工艺进行了评价研究。但是，尚未有将事故树分析法运用于炸药压装工艺爆炸事故的原因分析。因此，本文运用事故树分析法对炸药压装工艺发生爆炸事故的原因进行了分析，构建了炸药压装工艺爆炸事故树，通过求取事故树的最小割集和最小径集以及各基本事件的结构重要度，对影响炸药压装工艺安全的主要因素进行了分析和总结，并有针对性地提出了安全技术控制措施。

1 炸药压装工艺概述

炸药压装工艺是指在压力机上，通过冲头施加一定强度的压力，将散粒炸药在模具或弹腔中压制成具有一定形状、密度和强度的药件或装药的方法。按照装入炸药的方法不同，可分为直接压装法和药柱分装法。

直接压装法是将散粒炸药直接压入弹腔，一般适用于弹壁较厚的穿甲弹和其他小口径弹，其工艺流程见图1。

图1 直接压装法工艺流程图Fig.1 Flow chart of the direct pressing process

药柱分装法是先将散粒炸药在专用模具中压制成药柱后，再用黏合剂将药柱固定于药室中，其工艺流程见图2。

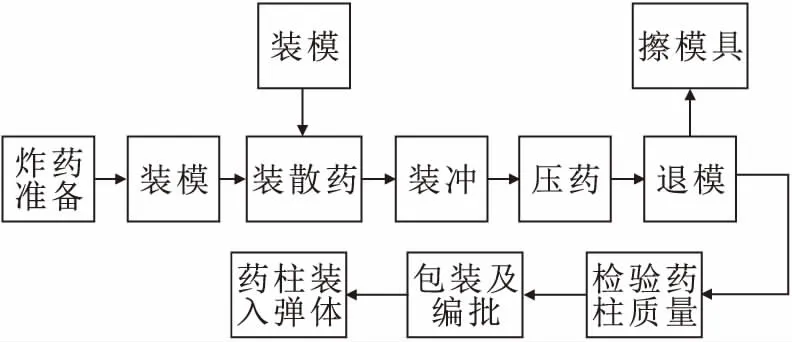
图2 药柱分装法工艺流程图Fig.2 Flow chart of the indirect pressing process

由于炸药压装过程是机械挤压过程，因此除了要求炸药有较低的机械感度外，还要有较好的成型性[4]。

2 炸药压装工艺爆炸事故树的建立

事故树分析法(Fault Tree Analysis,FTA)是安全系统工程的主要分析方法之一。该方法由美国贝尔电话研究所于1961年为研究民兵式导弹发射控制系统的安全性问题时提出，是一种描述导致灾害事故有关的各种因素之间因果关系和逻辑关系的分析方法[5]。事故树分析法能对各种系统的危险性进行辨识与评价，不仅能分析出事故的直接原因，而且能深入地揭示出事故的潜在原因，具有简明、形象化的特点[6]。针对炸药压装工艺，本文先确定顶上事件为爆炸事故，再结合现场调研情况和以往事故案例的分析结果，构建了炸药压装工艺爆炸事故树，见图3。图3中各符号所代表的基本事件详见表1[7-9]。

图3 炸药压装工艺爆炸事故树Fig.3 Fault tree of explosion accidents in explosive pressing process

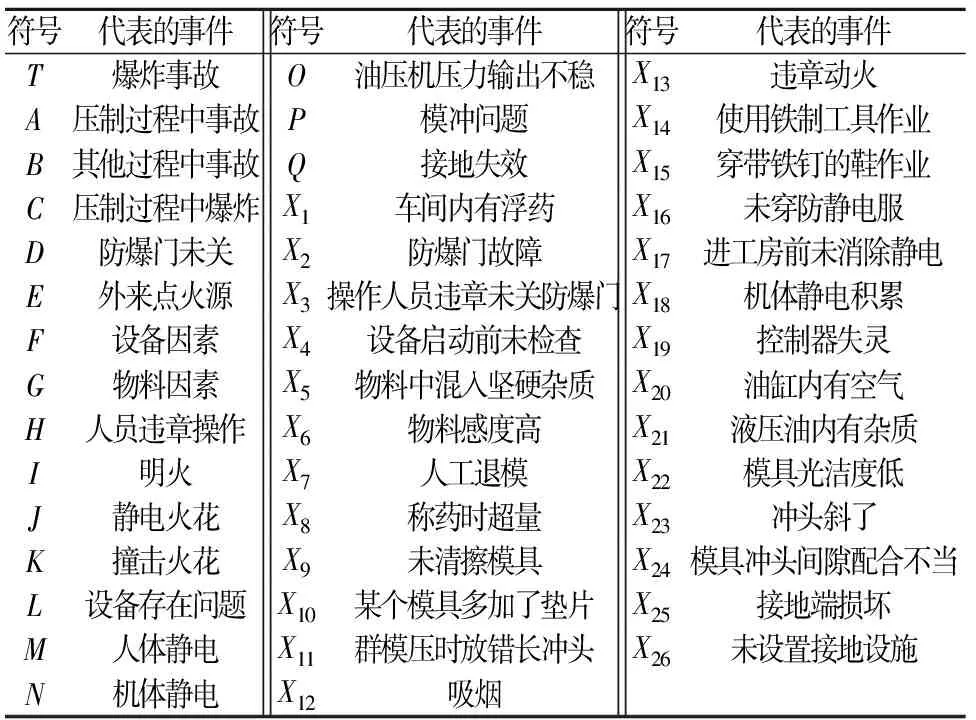
表1 炸药压装工艺爆炸事故树的符号及其代表的事件Table 1 Symbols of fault tree of explosion accidents in explosive pressing process and their representative events

3 炸药压装工艺爆炸事故树的分析

3.1 事故树定性分析

事故树定性分析主要是根据事故树的结构,分析各基本事件，其目的是求取事故树的最小割集和最小径集。通过计算发现，炸药压装工艺爆炸事故树的最小割集较多，共有34个，而最小径集只有9个，因此对该事故树采用最小径集进行分析。首先将该事故树转化为成功树，再运用布尔代数法求出最小径集[10]。成功树顶上事件T′ 的结构函数如下:

由上述成功树顶上事件T′的结构函数，可得出炸药压装工艺爆炸事故树的最小径集如下：

Q1={X1,X2,X3};

Q2={X1,X4,X5,X6,X7,X8,X9,X10,X11};

Q3={X1,X5,X6,X7,X8,X9,X10,X11,X19,X20,X21,X22,X23,X24};

Q4={X2,X3,X12,X13,X14,X15,X16,X17,X18};

Q5={X2,X3,X12,X13,X14,X15,X16,X17,X25,X26};

Q6={X4,X5,X6,X7,X8,X9,X10,X11,X12,X13,X14,X15,X16,X17,X18};

Q7={X4,X5,X6,X7,X8,X9,X10,X11,X12,X13,X14,X15,X16,X17,X25,X26};

Q8={X5,X6,X7,X8,X9,X10,X11,X12,X13,X14,X15,X16,X17,X18,X19,X20,X21,X22,X23,X24};

Q9={X5,X6,X7,X8,X9,X10,X11,X12,X13,X14,X15,X16,X17,X19,X20,X21,X22,X23,X24,X25,X26}

最小割集的定义表明，每一个最小割集都表示顶上事件发生的一种可能，事故树中有几个最小割集，顶上事件发生就有几种可能，从这个意义上讲，最小割集表示了系统的危险性，最小割集越多,说明系统的危险性越大。最小径集的定义表明，一个最小径集中所包含的基本事件都不发生，就可防止顶上事件发生，因此每一个最小径集都是保证事故树顶上事件不发生的条件，是采取预防措施防止发生事故的一种途径，从这个意义上来说，最小径集表示了系统的安全性。从上述分析可知，炸药压装工艺爆炸事故树的最小割集有34个，最小径集有9个，且每个最小径集中包含的基本事件均较多。由此说明，该工艺安全程度较低，容易导致顶上事件的发生[11-16]。

3.2 基本事件的结构重要度分析

结构重要度是指不考虑基本事件自身的发生概率，或者说假定各基本事件的发生概率相等，仅从结构上分析各个基本事件对顶上事件发生所产生的影响程度。基本事件的结构重要度越大，表示该基本事件对顶上事件的影响程度越大。基本事件结构重要度的计算公式如下：

式中:Iφ(i)为基本事件Xi的结构重要度系数;Kj为包含基本事件Xi的所有最小割集；nj为包含基本事件Xi的最小割集中的基本事件个数[17-19]。

经计算，可得炸药压装工艺爆炸事故树34个最小割集如下：

X1X12,X1X13,X1X14,X1X15,X1X16,X1X17,X1X18X25,X1X18X26,X2X5,X2X6,X2X7,X2X8,X2X9,X2X10,X2X11,X2X4X19,X2X4X20,X2X4X21,X2X4X22,X2X4X23,X2X4X24,X3X5,X3X6,X3X7,X3X8,X3X9,X3X10,X3X11,X3X4X19,X3X4X20,X3X4X21,X3X4X22,X3X4X23,X3X4X24

根据基本事件结构重要度计算公式，可计算得到各基本事件的结构重要度系数如下：

Iφ(1)=3.5，Iφ(2)=Iφ(3)=5，Iφ(4)=3，Iφ(5)=Iφ(6)=Iφ(7)=Iφ(8)=Iφ(9)=Iφ(10)=Iφ(11)=1，Iφ(12)=Iφ(13)=Iφ(14)=Iφ(15)=Iφ(16)=Iφ(17)=Iφ(18)=Iφ(19)=Iφ(20)=Iφ(21)=Iφ(22)=Iφ(23)=Iφ(24)=0.5，Iφ(25)=Iφ(26)=0.25

各基本事件结构重要度的排序为

Iφ(2)=Iφ(3)>Iφ(1)>Iφ(4)>Iφ(5)=Iφ(6)=Iφ(7)=Iφ(8)=Iφ(9)=Iφ(10)=Iφ(11)>Iφ(12)=Iφ(13)=Iφ(14)=Iφ(15)=Iφ(16)=Iφ(17)=Iφ(18)=Iφ(19)=Iφ(20)=Iφ(21)=Iφ(22)=Iφ(23)=Iφ(24)>Iφ(25)=Iφ(26)

由上述计算结果可以看出：基本事件X2、X3、X1、X4即“防爆门故障”、“操作人员违章未关防爆门”、“车间内有浮药”、“设备启动前未检查”的结构重要度较大，说明这4个基本事件对顶上事件发生的影响较大。因此，从本质安全的角度出发，在制定有针对性的安全技术控制措施时应重点关注这4个基本事件，但其他方面也不容忽视。

4 安全技术控制措施

综上分析可知，要想防止炸药压装工艺爆炸事故的发生，应从压制过程和其他过程两个方面着手，控制各基本事件的发生，特别是要控制X2、X3、X1、X4等结构重要度系数较大的基本事件的发生，以达到防止该事故发生的目的。对此，本文提出以下安全技术控制措施与建议：

(1) 压药、退模时须关好防爆门，禁止工作人员站在防爆门中心；在防爆门未关的情况下严禁开机；若防爆门发生故障，应及时停止操作并检修。

(2) 随时清擦模具、设备浮药，并清除散落在车间内的药粉，保持车间的干净整洁。

(3) 加强安全监管，禁止在车间内吸烟、使用铁制器具；作业人员操作时要轻拿轻放，严禁拖拉、碰撞、摩擦、敲打等操作行为，并严格执行动火规章制度。

(4) 在操作之前须先检查油压机、模具及其操作系统是否完好，并进行空车运行；同时检查设备工作状态及模冲配合情况，确认安全后才可进行操作。

(5) 定期检查防静电设施及其附件；作业人员工作时要穿好防静电服和防静电鞋。

(6) 压药模具的设计、制造、装配应合理到位，保证模冲间隙合适、模具的光洁度高；发现模具有划痕、毛刺等现象时应及时更换，并保证压药和退模安全。

(7) 物料在投入使用前须仔细检验与筛选，避免物料中混入坚硬杂质，导致物料感度增加；称量物料前须认真检查并校对天平，药杯与药勺要干净无损，保证称量准确。

(8) 加强对操作人员的安全培训，提高其安全意识，并要求其操作时严格遵循操作规程，严禁出现人工敲打退模等情况。

5 结 论

本文运用事故树分析法对炸药压装工艺爆炸事故的成因进行了分析，建立了炸药压装工艺爆炸事故树，并求取其最小割集和最小径集以及各基本事件的结构重要度，得出了导致炸药压药工艺爆炸事故的主要因素，并提出了有针对性的安全技术控制措施与建议。由于目前对炸药压装工艺爆炸事故的基本事件发生概率的研究还很匮乏，所以本文只对事故树进行了定性分析，若能获得可靠的事故树基本事件的发生概率，经过定量分析，将可得到更为精确的评价结果，这对预防顶上事故的发生并达到本质安全化生产有着重要的意义。

通讯作者：何中其(1978—)，男，博士，讲师，主要从事安全技术与安全工程方面的研究。E-mail： hzq555@163.com