基于多种数值分析方法的电压暂降凹陷域快速算法*

王晞，唐权，陈礼频，张玉鸿，阚力丰，李华强

(1．国网四川省电力公司 经济技术研究院，成都610041;2．四川大学 电气信息学院，成都610065)

0 引言

随着工业过程中大量敏感设备投入使用，电压暂降和短时中断对工业敏感用户造成的经济损失日趋严重［1-3］。国际电气和电子工程师协会(IEEE)定义电压暂降为电压有效值快速下降到额定值的90%-10%，持续时间为0．5 周波至 1min［4］的电能质量现象。电网故障是电压暂降的主要成因［5］，工业敏感用户是否受电压暂降的影响与自身敏感度、所处位置和电网故障点位置等因素有关［6］。电压暂降凹陷域是指系统故障引起电压暂降使系统中所关注的公共连接点(Point of Common Coupling，PCC)电压降至最低耐受电压幅值以下的故障点所在的区域［5］。电压暂降凹陷域识别的意义在于其对电网规划、改造以及工业敏感用户选址提供的理论依据和数据支撑。

现有的电压暂降凹陷域识别方法主要包括实测法和预估法［7-11］。实测法需要对电力系统和电力用户进行长期观测，其时间成本和经济成本都很高，可行性不强。文献［7］和文献［8-10］分别介绍了临界距离法和故障点法，但临界距离法适用于辐射型网络的计算，而不适用于环网计算;故障点法若要达到1%的精度则需在每条线路均匀设置100个故障点，且对于故障点的设置国内外尚无统一认识［8］。文献［11］提出一种利用暂降幅值解析计算式计算凹陷域的方法，遗憾的是其求解使用的数值处理方法单一，算法性能有待提高。

针对上述问题，提出一种基于多种数值分析方法的电压暂降凹陷域解法，详细阐述了凹陷域解析计算所涉及的数值分析方法。在保证计算准确度的前提下提高计算速度，为大型系统的凹陷域计算提供快速准确的计算方法。将临界故障点的求解问题简化为二次函数与暂降阈值的交点问题，并按根的个数分情况处理，避免逐一计算各线路故障导致敏感节点电压暂降的最大幅值和最小幅值，弥补了对所有线路采取同样的数值处理方法所导致的算法低效和局部不收敛的不足。

1 电压暂降幅值解析式

假设传输线路i－j上f点发生故障，用p表示故障距离，如图1所示。

图1 故障距离示意图Fig．1 Fault distance schematic diagram

式中p∈ [ 0 ，1 ] ;Lif为线路首端到故障点f的距离;Lij为线路首端到末端的距离。

电压暂降幅值解析式可用故障距离p为变量表示如下:

式中m表示所关注PCC节点;f为故障点;Zmf为所关注节点与故障点的互阻抗矩阵;Zff为故障点阻抗矩阵;0、1、2分别表示零序、正序和负序。

其中正、负、零序阻抗矩阵的计算方法文献［11］已做详细阐述，文中不再赘述。各类型故障情况下节点电压幅值计算式如式(4)～式(10)所示，其中不对称故障均以A相为基准相。

三相接地短路:单相接地短路:

式中 α =ej120°;下标 a，b，c分别代表系统中的A、B、C 相。

2 临界故障点计算

临界故障点计算是凹陷域识别的关键步骤［11］，而现有临界故障点计算使用的数值处理方法单一，算法性能较差。由前文所述易知，电压暂降幅值解析计算式是故障距离的二次函数，待求的临界故障点方程为高阶非线性方程。因此，在给定电压阈值的情况下，临界故障点的求解问题可等效为二次函数与电压阈值的交点问题，如图2所示。

图2 暂降幅值解析式与阈值的交点示意图Fig．2 Schematic diagram of the intersection of sag amplitude equation and threshold

2．1 根的个数问题

由图2可知，曲线1～3分别刻画了根个数为2个、1个(重根)和无根的情况。此外，在实际求解过程中，还伴随着根值无意义的情况，即pi＜0或pi＞1，此时需要视具体情况做区别处理。根的个数，可通过两种途径得到，一是利用搜索算法求得曲线中的最大值，通过比较最大值与暂降阈值的大小关系判定根的个数;二是利用插值方法求出暂降幅值对故障距离的显式表达式近似替代真实的幅值表达式，进一步利用判别式与根个数的关系判断，下面对两种方法展开解释。

2．1．1 最大值搜索算法

电压暂降幅值解析式是一种典型的一元单峰函数，黄金分割搜索法能快速求解一元单峰函数最值。该算法在函数定义区间内依据黄金分割比例对称取得一系列搜索点，通过计算和比较对应的函数值不断缩小搜索区间来逼近函数最值解和对应的最值［12-13］。通过黄金分割搜索算法求解最大暂降幅值对应的故障距离，求解步骤如下:

(1)确定搜索上界pu和下界pd，由式(11)计算故障距离p1和p2:

(2)将故障距离代入电压暂降幅值计算式得到V(p1)和V(p2);

(3)比较V(p1)和V(p2)的大小，若V(p1)＜V(p2)，则最大暂降幅值处于 ［p1，pu］内，令 pd=p1;反之最大暂降幅值则处于［pd，p2］，令pu=p2;

2．1．2 插值方法

牛顿插值法不但继承了迭代插值便于增加节点的优点，还能给出插值多项式的显式表达式［14］。由于暂降幅值表达式是故障距离p的二次函数，因此使用牛顿插值法时仅用到二阶均差即可，如式(12)所示，牛顿插值系数可由式(13)～式(15)计算得到。

在利用牛顿插值法得到暂降幅值显式表达式的基础上，将二次方程求根公式求出的根值作为弦割法迭代初值。

2．2 根的求解方法

非线性方程根的数值求解方法有很多:牛顿迭代法(如式(16)所示)收敛速度快，但它对导数表达式f'(xk)的要求在f(xk)未知的情况下难以满足;简化牛顿法(如式(17)所示)将f'(xk)用常数C替换，其计算性能依赖于常数C的选取，然而实际计算中合适的C值很难选取;弦割法(式(18)所示)较好地避免了上述问题，且其几何意义明确［14］，如图3所示。本文利用弦割法求解临界故障点:

图3 弦割法求解示意图Fig．3 Schematic diagram of secant method

过曲线 y=f(x) 上两点 Pk－1，Pk作直线 PkPk－1，将该直线与x轴交点横坐标xk+1作为根α新的近似值，该割线方程为:

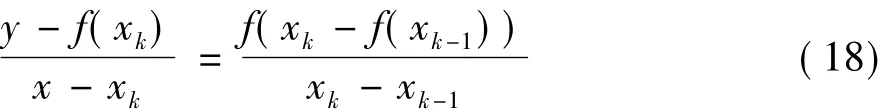
经整理可得:

经推导得到临界故障距离迭代表达式:

式中k为迭代次数;Vthre为电压暂降阈值。

3 基于数值分析理论的凹陷域求解方法

上述方法的适用场景、计算速度和迭代精度都不尽相同，因此本文提出基于数值分析理论的凹陷域求解方法旨在保证算法精度的前提下提高计算速度，以期为大型系统的计算提供帮助。

计算各节点故障时敏感节点s的暂降幅值，形成PCC点暂降幅值n维向量Vsag:

Vsag= ［V1s…Vns］T(21)

式中Vis为母线i故障时敏感负荷所在节点s的暂降幅值。

计算各节点故障时敏感节点暂降幅值与电压暂降阈值的差值，形成差值向量ΔVsag。通过判断该向量元素的正负可知各节点是否处在敏感节点的暂降凹陷域内，可以避免计算整条线路中引起暂降幅值最大和最小的点，从而节省了计算时间开支。

式中Vsag(i)为节点i的电压暂降幅值。

为便于计算，将ΔVsag大于等于0的母线标记为1，反之标记为0，并形成节点记号向量B。

相应地，将每条线路中:首端节点和末端节点都处在敏感节点的暂降凹陷域内的线路(以下简称“凹陷域”)标记为2;将一端处在凹陷域内的线路标记为1;首末端都不位于凹陷域中的线路记为0。由此可形成线路记号向量L。结合二次函数图像分析如下:

Case 1:L=0表示线路首末节点电压幅值均低于电压阈值，由二次函数的几何意义易知该条线路都不在凹陷域内;

Case 2:L=1表示线路首末节点有一个处于凹陷域内，该情况又可分为2种情况，如图4的1，2曲线所示。此时均需求解二次函数与阈值的另一个交点，使用牛顿插值法以线路首、末、中点故障距离和暂降幅值为插值点求解显式表达式，即(0，Vfrom)、(0．5，V0．5)和(1，Vto)，利用二次函数求根公式求该插值函数的根作为弦割法迭代的初始解;

图4 L=1时临界故障点示意图Fig．4 Critical fault point schematic diagram when L=1

Case 3:L=2表示线路首末节点暂降幅值均低于阈值，此时仅需通过确定暂降幅值的最大值与电压阈值的大小关系即可确定临界故障点个数。若暂降幅值最大值大于电压阈值则说明该线路有两个临界故障点;反之则表示该条线路完全处于凹陷域内。如图5所示，具体计算步骤如下:

(1)首先计算给定的系统的正、负、零节点阻抗矩阵，并使用式(4)～式(10)分别计算得到敏感负荷所在节点在各节点发生不同故障类型时电压暂降幅值;

(2)根据步骤(1)得到的敏感节点的暂降幅值向量Vsag，按照式(23)计算节点记号向量B和线路记号向量L，并开始逐条线路轮询。若Li为0说明此线路不在凹陷域内，则直接计算下一条线路;若Li为1则说明该条线路首末节点有一个处在凹陷域内，用牛顿插值法寻找暂降幅值的显式表达式;若Li为2则用黄金分割搜索法求解其最大值。将求得的最大值与电压阈值比较，若最大幅值小于等于阈值，则说明此线路处在凹陷域内，否则使用牛顿插值法利用(0，Vfrom) 、(pmax，Vmax) 和(1，Vto)三点求暂降幅值表达式。得到显式表达式后均采用弦割法迭代求解准确值;

(3)重复步骤(1)、步骤(2)直到完成系统所有线路的迭代或轮询，此时可得到给定阈值和敏感负荷节点下的电压暂降凹陷域。

图5 电压暂降凹陷域快速求解算法流程图Fig．5 Flowchart of fast solution algorithm for vulnerable area of voltage sag

算例使用的计算机 CPU为 Intel Celeron，2．9 GHZ，RAM 为2．00 GB，操作系统为64 位 Windows 7，仿真软件为Matlab 6．0。采用IEEE-30进行仿真分

4 算例分析

析。IEEE-30系统包含6台发电机组、30条母线、37条线路以及4台变压器，假设所有变压器均采用Y0/Y0接线方式，假设节点10为敏感负荷所在节点，如图6所示。

图6 IEEE30节点系统Fig．6 IEEE30-node system

在该系统中分别设置电压阈值为 0．8，0．7，0．6 p．u．。利用前文所述的计算方法，可得节点10对应的凹陷域如图7所示，图中所示凹陷域由外到内对应的电压阈值依次为 0．8、0．7、0．6。为对比各算法性能，本文采用三种方法求解该系统的节点10在电压阈值为0．8 p．u．时的凹陷域。三种方法依次是故障点法、单一数值解法和本文所述方法。限于篇幅，文中对各算法的对比分析仅以三相短路为例。

图7 三相短路时节点10对应的电压暂降凹陷域Fig．7 Vulnerable area of voltage sag corresponds to node-10 caused by three-phase short-circuit fault

设置故障点法的计算精度为0．01，对线路采用均匀设置故障点的方式，要达到0．01的精度需对每条线路均匀设置100个故障点。由于每条线路中的临界故障点最多两个，因此，文中将每条线路的凹陷域分为两个区间表示，如:线路1-2的凹陷域为［0．780，1］表示按1-2 的方向，从线路 0．780 的位置到线路末端均处于凹陷域内。部分线路的计算结果(含有临界故障点的线路)如表1所示。

表1 故障点法与本文方法部分计算结果对比Tab．1 Comparison of part of calculation results between fault position method and the proposed method

若以故障点法的计算结果为标准，表1中，单一数值解法的计算结果较故障点法有不同程度偏差，同等条件下，文中算法的计算结果更接近故障点法的计算结果。由于实际系统中线路分布情况更为复杂，因此对计算结果的精度要求更高。

各算法的性能对比如表2所示。不难发现，使用单一数值解法尽管在求解速度上较故障点法有一定提高，但由于其对每条线路均采取先插值得到显式表达式再求临界故障点的方式，算法低效、灵活性较差，且难以避免迭代不收敛情况的发生。

表2 各算法的性能对比Tab．2 Performance comparison of the algorithms

5 结束语

(1)利用电压暂降幅值解析计算式求解暂降凹陷域对于各种结构的系统具有广泛适用性，计算结果准确可靠;

(2)将临界故障点的求解简化为解析式二次函数与电压阈值的交点问题使该问题的几何意义明确化，在此基础上引入多种数值求解方法系统性求解，避免了对每条线路使用单一数值解法导致的算法低效性，大幅提升了算法性能。