基于多场耦合模型的海底电缆载流量和温度场计算研究
李萌,牛胜锁,刘玉芹,赵可为
(华北电力大学电力工程系,河北保定071003)
0 引言
近年来海上风电场的建设发展迅速,海上风电产业是海底电缆最主要的终端应用市场,作为其与陆地大电网连接的重要枢纽,海底电缆输电技术在我国有迫切的研究需要和工程应用前景,其中对海缆载流量的准确计算更是对优化海缆建设成本、提高海缆利用效率有着重要的意义。海底电缆的载流量是指其在给定的敷设方式和相应的环境条件下,稳态运行于最高允许工作温度下的载流能力。目前海底电缆多为交联聚乙烯(XLPE)电缆,其线芯导体所能承受的最高耐热工作温度为90℃。
常见的海底电缆载流量和温度场计算方法有两种[1]:一种是基于IEC 60287规范所制定的等效热阻法,该方法在计算单回路电缆直埋敷设时的载流量有着较高的计算效率和准确度,但由于其计算结果是基于电缆表面是等温面、地表为恒温边界等一系列假设所得出的,因此在进行多回路计算时结果较为保守,误差较大[2];另一种方法是数值解法,包括边界元法、差分法和有限元法等,该方法能准确模拟实际工况并进行多物理场的耦合计算,因此成为近几年来电缆载流量和温度场分析的主要研究手段[3]。
文献[4-11]利用有限元法对常见敷设方式下电缆的稳态温度场进行了研究分析,但实际工况中电缆的敷设条件并非都如此理想,以海缆近陆地升压站段为例,该路径段常见的敷设方式为电缆沟敷设,但电缆群并未严格放置在沟内角钢架上的不规则敷设方式十分常见,为保证海缆的安全运行,应对沟内电缆群分层敷设于角钢架上和不规则敷设于沟内底部的情况都进行分析计算。电缆群在电缆沟内敷设时涉及到热传导、热对流与热辐射三种传热方式的耦合,同时由于电缆线芯导体流过电流时会产生磁场,进而与周围电缆的发热相互影响,因此在针对该敷设方式进行研究时,需要应用基于电磁场、流体场与热场所搭建的多物理场耦合模型进行分析计算,文献[12]提到了该敷设情况,但在研究分析时忽略了沟内空气流动对散热的影响,目前对电缆沟内电缆群不规则敷设的分析仍鲜有研究。
本研究以工程中应用的交流三芯电缆HYJQF41-F-26/35 kV为例,搭建基于电磁场、流体场和传热场三物理场的耦合模型,重点研究了三回路海缆电缆沟内分层排列敷设于角钢架和敷设于沟底部时温度场的变化情况,同时利用迭代计算求得两种情况下的载流量值,分析了敷设方式选择对于电缆载流量的影响,对电缆在实际过程中的敷设安装和运行维护起到了良好的指导作用。
1 电缆的多场耦合模型与计算原理
为了提高模型的计算效率,现作出如下假设:
例如,人教版十二册《北京的春节》一课,课文中呈现许多儿化音,这在我们闽南地区是接触比较少的,因此,预习时,家长应该引导孩子多读读这样的词语,有助于把文章读通读顺,同时,课后还可以为孩子播放一些讲述老北京传统文化的电影,结合演员对话,来学学这些儿化音。这样不仅规范了孩子平时因为方言影响说得不标准的普通话,同时也激发了孩子研究语言文字表达的兴趣。
(1)相较于电缆的横截面,其长度可认为无限长,在不考虑电缆敷设时扭曲的情况下,可将计算问题简化为二维平面问题;
(2)电缆的线芯导体和金属护套的电导率随温度发生变化,其变化为:

式中ρ20为线芯导体在温度为20℃时的电阻率,单位为Ω·m;α20为线芯导体的电阻温度系数,单位为1/K。
1.1 温度场模型
在建立电缆温度场数学模型时,应对电缆沟内传热过程进行分析,其中电缆是唯一热源,其发热来自于线芯导体通电产生的焦耳热和介质损耗产生的热量。沟内散热过程包含两个方面:其中电缆本体、支架以及电缆沟壁与壁外土壤间以热传导为主要传热方式,沟内电缆和支架与沟内空气、沟表面盖板与板外空气间以热对流和热辐射为主要传热方式。对于具有内热源的区域(如线芯导体,金属护套和铠装层)[13],其热传递微分方程如式(2)所示;对于无内热源的区域(如电缆内部其他介质层和外部土壤、空气等),其热传递微分方程如式(3)所示;对于电缆沟内的热辐射传热方式,其热传递微分方程为:

式中Qi是面单元i的传热率;δ是Stefan-Bolzman常数;εi是面单元i的有效热辐射率;Fij是面单元i与j的角系数;Aij是面单元i的面积;Ti和Tj是面单元i和j的绝对温度值。
1.2 边界条件
由于有限元法对于开域场不易求解,为了保证多场耦合模型的计算效率与准确性,现将其转变为等效闭域场进行求解。从传热学的角度可知,距离热源越远的区域温度变化越小[14],从现有研究成果可查,一般认为电缆发热对距离其2 m以外的土壤影响就已十分微弱,现为保证计算准确性,现设定距离沟壁底部2 m处为求解域的下边界,距离沟壁左右两侧3 m处为求解域左右边界,求解域上边界即为电缆沟盖板。
在进行模型求解计算时,需要确定对应的边界条件,在热力学中,常见的边界条件可以分为以下三类[14]:第一类边界规定了边界上的温度值,即边界温度保持常数,其数学描述如式(5)所示;第二类边界条件规定了边界上的热流密度值,即边界热流密度保持定值,其数学描述如式(6)所示;第三类边界条件规定了边界上物体与周围流体间的表面传热系数h与周围流体的温度t,其数学描述如式(7)所示。
式中φ(x,y)表示已知温度的求解域对应的温度函数;τ表示单元边界;f(x,y,t)是已知温度的边界求解域对应的温度函数;g(x,y,t)是边界上热流密度向量函数。

本次研究以35 kV海缆在电缆沟内单回路和多回路敷设为例进行分析,沟内涉及三种传热方式,其温度场计算可由式(1)~式(4)求解,沟内左右边界处温度无变化,属于第二类边界条件,下边界为深层土壤,一般认为温度为定值,属于第一类边界条件,上边界为地平面,符合对流换热条件,属于第三类边界条件,各边界条件可由式(5)~式(7)求解。
2 实例分析
2.1 电缆实例参数
以电缆沟内敷设电缆的情况为例,搭建多物理场耦合模型对其进行载流量和温度场的分析计算,其两种敷设情况下的模型截面图如图1所示。电缆沟为1 m×1 m的方形,盖板是尺寸为1.2 m×0.1 m的矩形,沟内角钢架厚度为5 mm,支架间间距为0.225 m。敷设电缆型号为HYJQF41-F-26/35kV 3×70 mm2XLPE电力电缆,结构参数如表1所示。电缆敷设环境参数如表2所示。

图1 两种敷设情况下的电缆模型Fig.1 Geometric modeling of cable channel under two laying situations
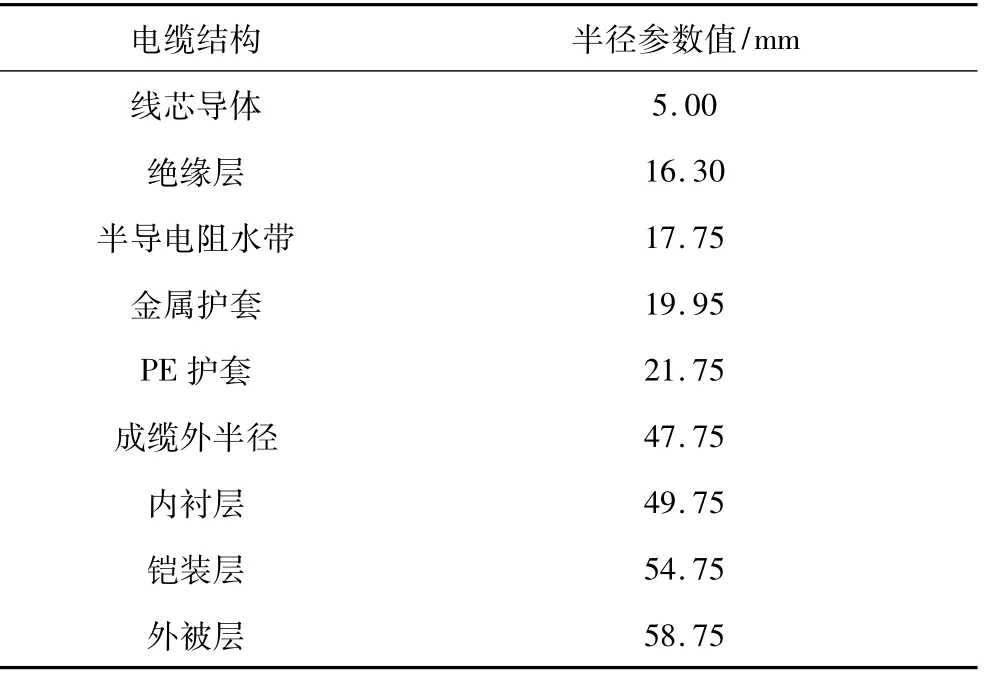
表1 电缆结构参数Tab.1 Cable structure parameters

表2 电缆敷设环境参数Tab.2 Environmental parameters of cable laying situation
2.2 模型设置条件
在进行模型求解时不考虑三相电流的不平衡带来的影响,同时对电缆内各线芯导体施加幅值相同,相位相差120°的电流值,并在z轴方向施加耦合电压。另外电缆内部金属护套采取两端接地方式,不产生环流。
2.3 计算结果与分析
2.3.1 单回路电缆电缆沟内敷设时结果分析
以工程中采用的 HYJQF41-F-26/35kV 3×70 mm2XLPE电力电缆为例,环境参数同表2,单回路敷设于电缆沟内,在电缆线芯导体稳定通入300 A电流的条件下,通过搭建模型计算电缆温度场分布,并与IEC 60287计算结果、现场试验数据进行对比。
图2为线芯流过300 A电流时单回路电缆沟内区域的温度场分布图。从图中可看出,由于线芯导体产生的焦耳热为主要热源,电缆的最高温度出现在线芯导体区域,为78.012℃,且温度从线芯向外逐渐降低,电缆外表面温度为52.791℃。同时,在相同条件下,IEC 60287标准计算求得的线芯导体温度为81.594℃,试验测得数据为79.360℃。多场耦合模型求得的线芯导体温度分别与IEC 60287和试验数据相差4.5%、1.7%,三种方法的结果误差在工程的需求范围内(±5%),但仿真结果与IEC方法计算结果误差相对较大,通过分析得出产生误差的原因如下:IEC方法在计算电缆各层温度的过程中忽略了温度变化对电缆各层材料参数的影响;IEC方法在计算时忽略了空气流动对散热产生的影响。基于以上两方面原因,导致在进行单回路电缆敷设载流量计算时,IEC方法计算结果较为保守。针对以上问题,文章建立的基于电磁场、流体场和传热场的耦合模型能够很好地实现对实际工况的模拟,且仿真结果与试验数据接近,进一步表明了该耦合模型在准确计算多回路电缆敷设时电缆的载流量和温度场分布时可以达到要求的计算精度。
同时利用COMSOL软件内的优化算法迭代计算求解电缆载流量,设定线芯导体的最高温度Maxtemp为90℃,相对容差为0.1,经过迭代计算求得载流量值为312.5 A,此时温度场分布图和沟内空气流速分布图分别如图3和图4所示。

图2 单回路电缆沟敷设时电缆温度场分布图(电流为300 A)Fig.2 Temperature distribution of single loop cable with current of 300 A
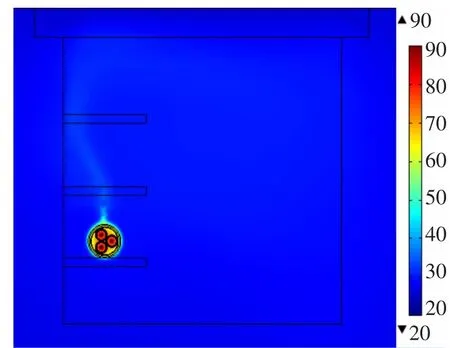
图3 单回路电缆沟敷设时电缆温度场分布图(载流量值为312.5 A)Fig.3 Temperature distribution of single loop cable with current of 312.5 A
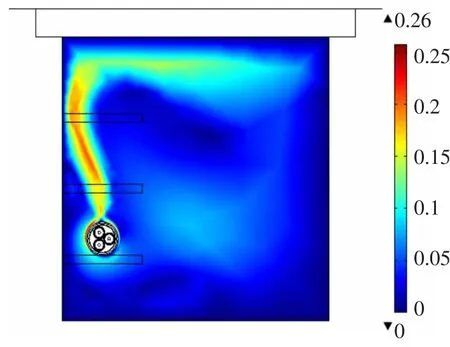
图4 单回路电缆沟敷设时空气流速分布图(载流量值为312.5 A)Fig.4 Air velocity distribution of single loop cable with current of 312.5 A
2.3.2 三回路电缆分层敷设于电缆沟内的载流量计算分析
三回路电缆规则敷设于电缆沟内的角钢架上,各线芯导体流过的初始电流为250 A,此时线芯导体能达到的最高温度为77.614℃。通过迭代计算求得该敷设方式下电缆的载流量值为283.1 A,其中图5为载流量值下三回路电缆群的温度场分布图,三回路电缆的线芯导体温度最大值从上到下分别为89.913 ℃、88.763 ℃、86.924 ℃;图6 为该敷设方式下电缆沟内的空气流速分布图,其中最大空气流速为 0.47 m/s。

图5 三回路电缆规则敷设时温度场分布图(载流量值为283.1 A)Fig.5 Temperature distribution of triple loop cables with current of 283.1 A

图6 三回路电缆规则敷设时空气流速分布图(载流量值为283.1 A)Fig.6 Air velocity distribution of triple loop cables with current of 283.1 A
2.3.3 三回路电缆敷设于电缆沟底部时的载流量计算分析
将三回路随机敷设于电缆沟底部,同样流过的初始电流值为250 A,此时各线芯导体的最高温度为86.6℃。利用迭代算法求得电缆载流量值为257.2 A,图7为该敷设方式下电缆载流量值下的温度场分布图,其中三回路线芯导体温度的最大值从左往右分别为83.040 ℃、90.090 ℃和87.510 ℃,图8为沟内空气流速分布图,其中最大空气流速为0.34 m/s。
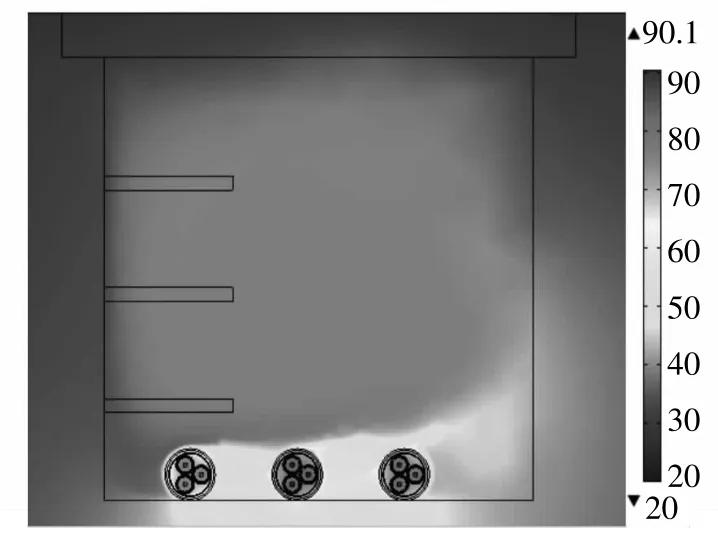
图7 三回路电缆底部敷设时温度场分布图(载流量值为257.2 A)Fig.7 Temperature distribution of triple loop cables with current of 257.2 A
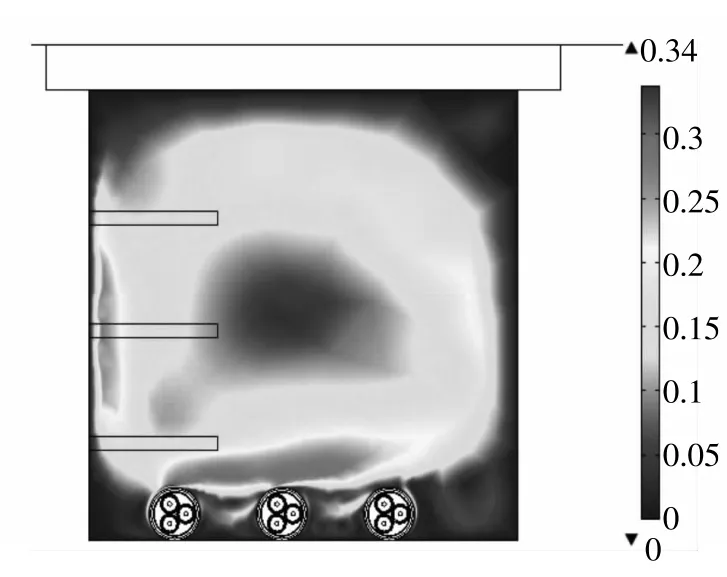
图8 三回路电缆底部敷设时空气流速分布图(载流量值为257.2 A)Fig.8 Air velocity distribution of triple loop cables with current of 257.2 A
通过图2和图5对比发现,当电缆沟内敷设电缆回路数增加至三回时,电缆的载流量值下降了9.4%,继续增加回路数电缆载流量会进一步下降,因此可以推断,在规范敷设方式下,回路数的增加会降低电缆载流量值,且与回路数量呈现非线性反比关系;同时通过图5和图7的对比发现,三回路海缆敷设于底部时电缆载流量值相较规范敷设下降了9.2%,可以推断敷设方式的选择对电缆载流量同样有着重要影响。因此在实际工程中,应严格按照规范对电缆进行敷设,最大程度保证在相同条件下电缆的温升与运行可靠性之间的平衡。
3 结束语
基于文章开头的两点假设,建立了基于电磁场、流体场和传热场的多物理场二维耦合模型,在充分考虑了多种传热方式和空气流速等因素影响的前提下,提出了一种可以有效模拟各敷设环境下电缆载流量和温度场分布的方法,并以交流三芯海底电缆为例着重分析了不同敷设方式对电缆载流量和温度场的影响,得出如下结论:
(1)电缆的敷设回路数与载流量值有着密切联系,回路数越多,电缆载流量值越小,因此在实际敷设时应将回路数确定在合适的范围内;
(2)在电缆沟等封闭敷设环境内,空气流动对电缆散热起到了积极作用,因此在实际敷设时适当在敷设区域内增加出风口或者引入通风设备,均可以有效降低电缆温升,从而提升电缆载流量;
(3)在电缆沟敷设时,敷设方式的选择对电缆载流量值同样有着显著影响,以三回路交流三芯电缆为例,通过仿真结果可以发现,敷设于电缆沟底部时电缆的载流量相较敷设于支架上下降了9.2%,因此在实际敷设时应按照施工规范分层敷设,从而在保证输电效率同时,延长电缆的使用寿命。

