全液压矫直机伺服系统动态特性的联合仿真研究
王 晶,王 凯,柳 渊,韩贺永
(太原科技大学,山西 太原,030024)
0 前言
矫直技术被广泛地应用在中厚板的生产过程中,成为板形控制中不可或缺的一种手段,矫直机性能的好坏直接关系到产品的质量。新一代的全液压矫直机具有结构简单、响应速度快、控制精度高等优点,近年来,客户对板形质量要求的提高,使其正逐步替代电动压下式矫直机[1]。
当矫直机矫直不同板型时,由于所需矫直力不同,从而导致系统参数、外部负载均发生变化,系统的非线性和复杂性提高,用传统的PID控制已经不能精准的描述系统的控制过程[2]。由于模糊控制理论对于系统数学模型不需要特别精确,并且模糊控制理论对参数的变化有较强的鲁棒性,在非线性、时变及滞后问题上,鲁棒性有很好的解决效果[3]。因此,本文中分析的全液压矫直机伺服系统动态特性,是以模糊控制理论为基础。
目前液压系统的模型仿真主要应用Matlab/Simulink和AMEsim两种软件。运用Simulink软件中的各种控制模块可以满足使用者在控制思想和控制策略的要求,但是在计算传递函数时,由于存在各种假设条件,所以不能精确表达现场实际情况[4]。运用AMEsim软件进行仿真时,可以依照现场情况选择所需元件,设置元件的各种参数,使其与现状工作条件尽可能的相似,但是在搭建控制系统时存在一定缺陷,尤其是在构建自适应模糊PID的控制器时不能充分满足需要[5]。AMEsim与Simulink进行联合仿真,既能够按照现场实际情况在AMEsim软件中设置液压缸和液压阀的相关参数,又可以利用Simulink中模糊控制箱,通过编写模糊控制规则,利用模糊控制实现PID参数的在线调整,使仿真结果更加接近实际的生产过程,使得理论分析有据可依[6]。本文在此基础之上进行建模,在建立联合仿真模型时以模糊控制理论为基础,将系统参数的在线调整引入二级控制中。因此,利用联合仿真模型得到的仿真结果将更加接近于实际效果。
1 模型建立
在搭建联合仿真模型时,以模糊控制理论为基础。搭建模糊控制器有两种方法,一种是将模糊控制器用于前向通道,一种是将模糊控制器用于反馈通道。当模糊控制器处于前向通道时,误差信号取自对象输出值与给定值之差,此时,由于模糊控制存在滞后性,这样会使伺服系统的控制精度与响应速度降低,这与实际需求不符[7]。
当模糊控制器放在反馈通道上时,其误差信号取自参考模型与对象输出的差值,这样将减小误差,从而提高模糊控制器的响应速度和控制精度。参考模型为根据经典控制理论计算得出的系统的闭环传递函数,即由一个惯性环节和一个二阶振荡环节组成[8]。
本文在此基础之上,将模糊控制器置于反馈通道上,误差信号取自参考模型与AMEsim模型的差值。模糊控制器为二维模糊控制,需要有误差和误差变化率两个输入变量,输出变量为Δkp,Δkd,Δki,为了实现PID参数的实时在线调整,所以将输出变量直接输入到PID各项参数中,如图1所示。
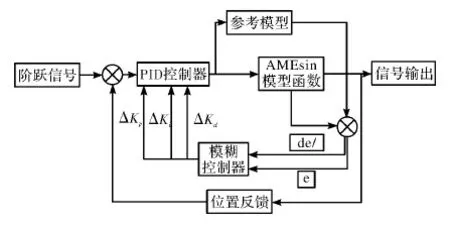
图1 系统流程图
1.1 参考模型建立
参考模型的系统闭环传递函数是由经典控制理论计算所得的。目前国外西马克等矫直机液压系统利用减压阀为液压缸的有杆腔提供恒定背压的方式[9],而无杆腔与伺服阀A口连接,伺服阀的B口封死。本文所研究的多变量系统是一个四自由度耦合而成的,此多变量系统构成了矫直机液压伺服系统。此液压伺服系统核心是4个液压缸的位置控制,其中有四缸同步、入口侧两缸和出口侧两缸倾斜等功能[10]。为了能够提高液压系统的固有频率、液压缸的响应速度,便于简化液压伺服系统的传递函数,液压系统采用液压缸的有杆腔去掉背压且直接与伺服阀的B口连接的方式[11]。
利用液压缸输出力与负载的力平衡方程、液压阀的流量方程和液压缸流量连续性方程推导液压系统传递函数[12]。矫直机液压伺服系统的核心部分是非对称四边滑阀控制非对称液压缸,如图2所示。根据参考文献[13-15]可得阀的流量方程为
QL=Kqxv-KcPL
(1)
式中,Kq为阀的流量增益;Kc为阀的流量-压力系数;xv为阀芯位移;PL为系统负载压力。
液压缸流量连续性方程为
(2)
式中,A1为液压缸活塞面积;Ctp为液压缸总泄漏系数;βe为油液体积弹性模量;Vt为液压缸控制腔的容积。
液压缸输出力与负载力平衡方程为
(3)
式中,mt为活塞及负载折算到活塞上的总质量;BP为活塞及负载的粘性阻尼系数;K为负载弹簧刚度;FL为作用在活塞上的任意外负载力。

图2 非对称阀控制非对称缸模型
联立方程(1)~(3),消去中间变量,得到活塞总输出位移与液压阀输入位移和外负载力的关系
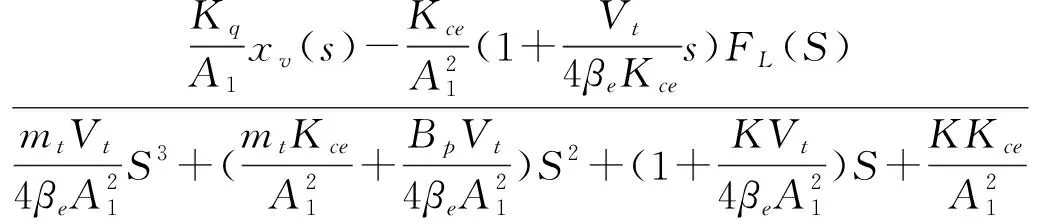
(4)
1.2 模糊控制模型建立
在矫直机对不同板材进行矫直的过程中,为被控对象随着负载变化和干扰因素的影响,其特性参数或结构发生改变,为提高控制效果,应当根据实际情况对PID参数进行实时在线调整。为了方便计算机能够根据现场实际情况自动调整PID参数,将操作人员的调整经验作为知识存入计算机中。但由于操作者经验、各种信号量和不
易定量表示的评价指标难以准确描述,所以用模糊集通过模糊数学基本理论和方法把规则的条件和操作表示出来,并把这些模糊控制规则及相关信息(如评价指标、初始PID参数等)作为知识存入计算机,为了实现PID参数的最佳调整,计算机根据控制系统的实际响应情况进行推理[16]。
邹庆鹏在致辞中介绍,河南作为中国农业大省,亦是全国农药生产、经营、使用大省。当前,河南省共有165家农药生产企业,年产农药约为2.6万吨,农药经营单位3.5万多家,年农药使用近1.7万吨。自新的《农药管理条例》实施以来,河南将贯彻落实新条例作为本省农业发展的一项重要任务,加大相关规章制度宣传工作,加强农药监管巡查工作,助力农药产业转型升级,力促农药企业做大做强,切实发挥保障国家粮食安全压舱石的作用。
本文选用二维模糊控制器,以误差E和误差变化EC为输入量,以Δkp,Δki,Δkd为输出量,使不同时刻的E和EC根据模糊规则对PID控制器参数进行实时在线调整,其结构如图3所示。

图3 自适应模糊结构图
该控制系统调整原则为
(1)当误差|E|较大时,为了让系统以最快的速度满足要求值,此时Δkp应取较大值,Δkd应取较小值,为了防止超调的出现,Δki取较小值。
(2)当误差|E|处于中等大小时,这时的系统已经快要满足要求值,为了防止超调的出现,Δkp应取较小值,同时Δkd取值要适中。
(3)当误差|E|较小时,此时系统已经接近要求值,此时Δkp与Δki取值较大,是为保证系统的稳态性能。
(4)当|EC|较小时,Δkd取值较大,当|EC|较大时,Δkd取值较小,是为保证系统的抗干扰性。
1.3 联合仿真模型建立(图4)
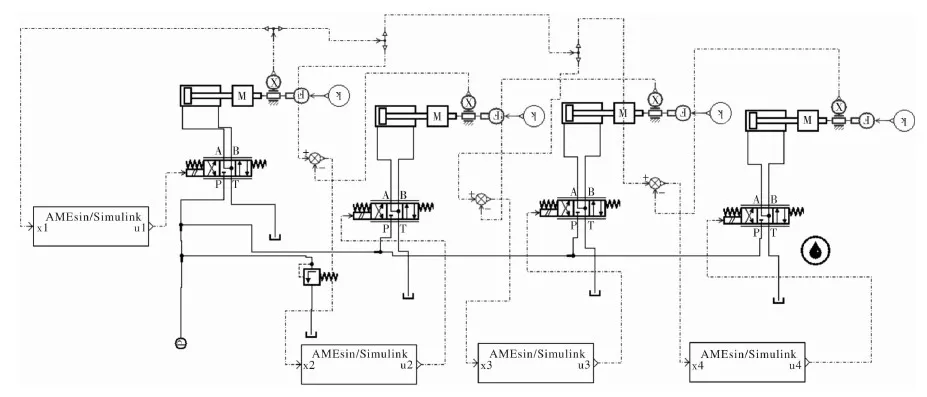
图4 AMEsim仿真模型
在建立联合仿真模型时,在模型二级控制中加入参数在线调整功能,在模型的研究中,模糊控制器的输入量是仿真模型与系统输出值的差值。将经典控制理论的传递函数与现代控制理论的模糊控制结合到一起。这样做是为了消除传统PID控制参数不能进行实时在线调整的不足和自适应控制对于模型辨识精确度要求高的弊端,在搭建联合仿真模型时,首先,在AMEsim中根据一缸主动其余三缸随动的原则搭建AMEsim模型,根据现场使用情况设置阀与缸的各项参数。
2 仿真结果与分析
根据实际使用情况设置液压缸活塞直径为640 mm,活塞杆直径为485 mm,外负载压力为7.5×106N,液压阀的频宽为100 Hz,流量为200 L/min,阀口压降为1 MPa。矫直机设计最大矫直力为3×107N,由四个伺服液压缸提供。因此单缸最大外负载为7.5×106N。

图5 外载荷为4.0×106 N三种仿真方法系统响应时间
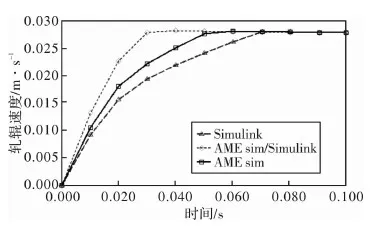
图6 外载荷为5.5×106 N三种仿真方法系统响应时间
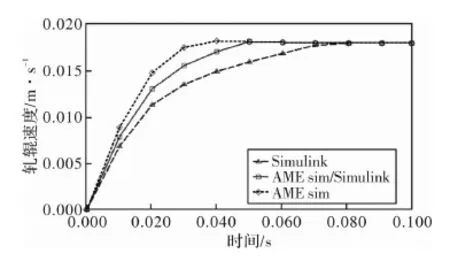
图7 外载荷为7.0×106 N三种仿真方法系统响应时间
从图5~图7中能够得出,采用Simulink仿真时,系统阶跃响应最快。采用AMEsim仿真,系统阶跃响应最慢。而联合仿真的响应时间居于二者之间。分析上述结果,因为计算传递函数时有众多假设条件,也就是在理想状况下进行的Simulink仿真,所以动态响应最快的,是采用Simulink仿真;因为液压阀和缸的参数都是严格按照现场实际参数设定,但是其控制部分比较简单,存在一定缺陷,所以采用AMEsim仿真时,动态响应有所延迟;采用AMEsim/Simulink联合仿真时,一方面可以在Sminlink中搭建理想的控制模型,又可以在AMEsim中设置系统元件的各项参数可以根据现场设备实际工作环境。在建立联合仿真模型时,建立模糊自适应PID控制器可以根据模糊控制原理,同时在仿真模型里将二级控制模型中的参数在线调整功能引入,为了使设备始终处于最佳工作状态,动态响应结果与其他两种仿真方式相比更加接近实际状态,因此要仿真模型根据现场实际情况实时在线调整PID控制器的参数。
3 现场实验研究
以某钢厂中厚板车间11-φ285/300 mm×3500 mm全液压矫直机为实验平台,液压伺服系统采用Rextorh 4WRDE16V200L高频响阀,阀的响应频率在5%的控制信号时,频宽为100 Hz,阀口压降为1 MPa,系统采用MTS位移传感器,所有检测到的位移信号直接进入高频响阀的专用模块,这样可以保证信号的真实性与准确性。设定液压缸的位移为0.1 mm,而矫直机伺服液压缸单缸输出力通过溢流阀可以调定为5.5×106N,如图8所示为系统响应曲线。
液压缸从8 ms开始运动,液压缸在50 ms时到达指定位置,虽然液压系统存在滞后性,但是响应时间符合工艺的技术要求。分析运动图像,液压缸在运动开始时不稳定,速度较快,是由于压力、流量对系统冲击较大;但是到了中期液压缸运动尽快达到平稳,速度有所减缓,因为控制器里将位移传感器的位移信号传入时,输入信号和反馈信号经过控制系统的比对后,调整了控制参数,校正了液压缸的运动;后期为确保系统的快速响应,使液压缸尽快到达指定位置,速度有所加快。液压缸的位置控制在0.098~0.1 mm之间,虽然位置有波动,但是符合控制精度要求。

图8 系统响应曲线
伺服系统单缸输出力是由溢流阀调定的,利用溢流阀压将伺服系统单缸输出力分别调定为4.0×106N、5.5×106N和7.0×106N,比较现场实际采集数据和仿真结果,如图9所示。
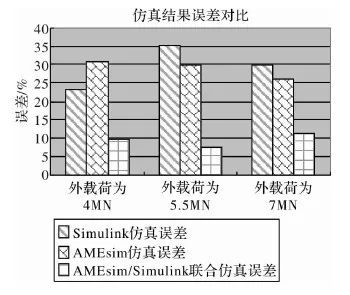
图9 实测结果与仿真结果对比
分析现场采集数据和仿真结果,Simulink仿真平均误差为29.2%,当产生的误差最大为35.2%时,单缸输出力为5.5×106N;AMEsim仿真平均误差为28.8%,当产生的误差最大为30.8%时,单缸输出力为4.0×106N时;AMEsim/Simulink联合仿真平均误差为9.4%,当产生的误差最大为11.1%时,单缸输出力为7.0×106N时。将三种仿真方式进行对比,最接近现场采集的数据的是联合仿真的结果。这是因为,一方面,在联合仿真模型中引入二级控制中参数在线调整功能;另一方面联合仿真在搭建模型时,不管是从系统元件的参数设置,还是控制模型的建立上都与实际情况最接近。为了与实际所用控制系统产生的效果相近,利用了模糊控制原理对控制参数实现实时在线调整,使仿真模型更加完善。
虽然联合仿真结果接近现场采集数据,但是两者之间仍然存在误差。一方面由于仿真时对于实际现场工作中存在压力冲击、管路振动等不稳定因素不能够完全仿真;另一方面联合仿真所采用的参数在线调整方法不是实际现场所采用的调整方法。
4 结论
(1)本文通过对比单缸输出力为4 MN、5.5 MN和7 MN三种不同状态下系统动态响应的仿真结果与现场采集数据,得出联合仿真的误差最小,其平均误差为9.4%,证明了联合仿真的可行性与可信度。
(2)比较Simulink、AMEsim和AMEsim/Simulink联合仿真三种仿真模型,Simulink仿真模型在计算传递函数时存在一些假设,仿真结果处于理想状态,系统动态响应最快;AMEsim仿真模型在搭建控制模型时,存在一定缺陷,系统动态响应较慢;AMEsim/Simulink联合仿真既可以按照实际情况设置系统元件参数,又可以搭建完整的控制模型,仿真结果最接近应用实际。
(3)本文在建立联合仿真模型时,虽然以矫直机为研究对象,但是其模型的搭建与参数的设置具有普遍特性。该建模思想可以运用于其他大流量、大负载、非线性特性明显的机构建模仿真中。

