基于负荷预测的冰蓄冷空调系统优化运行

徐笑强 陈振乾

东南大学能源与环境学院

冰蓄冷空调系统通常应用在办公楼，大型商场，宾馆，饭店和医院等负荷变化较大的场合[1]。它主要有两个优点：1）降低装机容量，从而减少制冷主机和电力增容费用。2）在实行峰谷电价的城市，因充分使用低谷电，冰蓄冷空调可大大节约运行费用。由于冰蓄冷空调系统比常规空调多出许多额外的设备，系统结构复杂，对自控的要求也更高[2]。如果在运行中其策略或控制方法选择不适，会导致移峰填谷的优势没有完全发挥，造成运行节约的经济未达到预期目标，使得该技术的推广受到一定的限制。

本文根据某冰蓄冷空调系统，针对其目前使用的主机优先供冷的运行控制方式加以改进，以神经网络预测建筑冷负荷作为基础，通过优化算法合理分配制冷主机和蓄冰装置逐时供冷量，从而得到经济最优化的运行方式。

1 建筑负荷实测

本文先对位于淮安的某办公建筑冰蓄冷空调系统的逐时供冷量和室外温湿度进行测试，测试时间从2016年8月5日至8月18日，共计317个小时。测试工具为ZUF-100型超声波能量表和RC-4HC型温湿度测量仪，测得的数据如图1和图2所示。

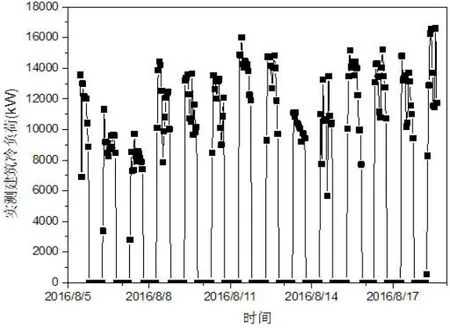
图1 实测建筑冷负荷

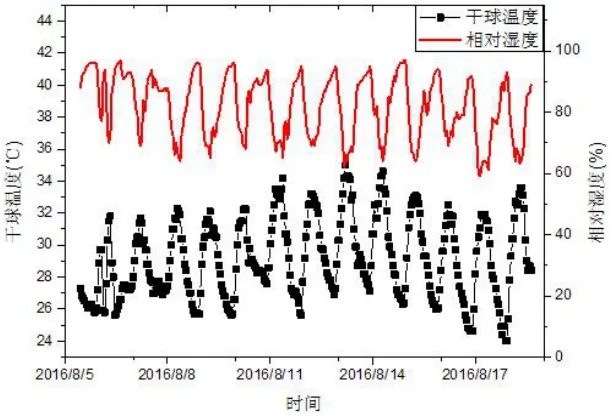
图2 实测干球温度和相对湿度

2 负荷预测

建筑冷负荷是与多种因素相关的非线性系统，而人工神经网络（Artificial Neural Network，ANN）对于此类系统在模型建立方面具有较好的适应性，同一种结构几乎不需要修改就能在不同建筑中使用[3]。因此本文选用ANN作为淮安办公建筑冷负荷预测的工具。

2.1 结构与参数的选择

ANN隐含层个数和各隐含层神经元个数的选取目前还没有统一的准则。Kawashima指出隐含层可按照2n+1（n为输入层神经元个数）选取[4]。人工神经网络的BP算法最具影响力，据统计，有近90%的神经网络采用这一方法[5]。本文选用具有13个神经元隐含层的BP神经网络预测冷负荷。

为了简化办公建筑的负荷预测，本文将从建筑物冷负荷影响因素主要有内扰和外部环境两个部分进行分析。虽然内扰在夏季负荷中占较大比重，可是在正常工作日，它跟作息时间有关，因此本文使用时间来体现内扰的影响。石磊[6]对外部环境与冷负荷的相关性做出了研究，研究表明，室外干球温度和湿度对冷负荷具有较强的线性相关性，而太阳辐射与冷负荷成非线性相关。考虑到实际测量和影响权重，将室外空气干球温度、湿度作为输入参数。本文最后确定选用BP神经网络输入层6组参数为：星期、时刻、k时刻室外干球温度、k-1时刻室外干球温度、k-2时刻室外干球温度、k时刻室外空气相对湿度。输出层1组参数，为建筑物k时刻的逐时冷负荷。

2.2 冷负荷预测评估

将6组输入参数和1组输出参数归一化处理后，统一导入MATLAB神经网络工具箱中进行训练。选取前250 h数据用于训练神经网络，后67 h数据用于验证网络准确度。

MATLAB神经网络工具箱在预测负荷时，阀值和权值随机产生，所以每次预测的值会有所差别。因为隐含层的层数无法确定，所以本文分别将一至五层隐含层，用相同数据每层预测30次，研究不同个数隐含层对预测结果的影响。为了量化分析不同结构的BP神经网络预测精度，分别使用了三个指标来评价预测结果。

1）相对误差δ

此处相对误差指的是预测总量与实测总量的相对误差。能量表实际测得最后67 h内空调总负荷共为430258 kWh，而将预测总负荷的相对误差从小到大依次排列，结果如图3所示。

图3 预测总负荷相对误差

2）均方根误差mse

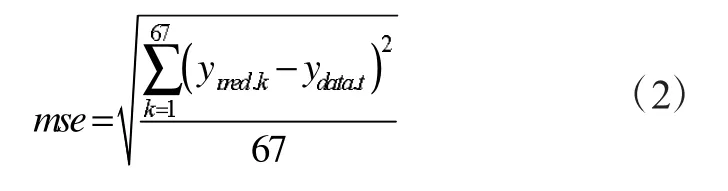
此处均方根误差指的是预测值与实测值的分散程度。将每组数据与实际测得的逐时负荷进行比较，计算出均方根σ，从小到大依次排列，则可以看到结果如图4所示。

图4 预测均方根误差

3）相关系数 ρXY

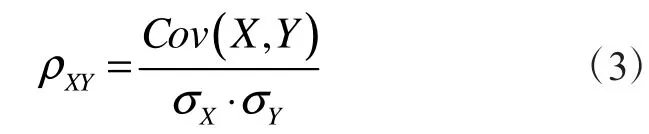
相关系数是两个测量变量之间关联变化程度的指标。将每组数据与实际测得的逐时负荷进行比较，并计算出相关系数，从小到大依次排列，则结果如图5所示。

图5 预测相关系数

将上述各个隐含层预测数据整理，取各指标平均值结果如表1所示。

表1 指标平均值评估

图6 预测数据平均值

由表1可知，1个和2个隐含层的神经网络预测效果较好。BP神经网络在单次预测中有可能出现极端值，对于冰蓄冷空调系统的优化运行极为不利，为了避免这种情况，本文首先剔除数据中的负数，然后取30次逐时预测冷负荷的平均值，其结果如图6所示。

采用和上述三个指标对预测数据平均值进行评估，发现经过处理后的预测数据平均值评估结果要远远优于指标平均的结果，如表2所示。

3 经济最优运行方式

最优化问题从数学角度来讲就是一个将实际问题转化为求一元或多元函数的极值的问题[7]。用最优化原理解决客观问题，一般经历两个步骤：建立数学模型和数学求解。

3.1 建立数学模型

冰蓄冷空调系统的优化实际上是在满足建筑空调负荷的条件下对主机供冷量和蓄冰槽供冷量的合理分配，从而达到运行费用最低的目标。因此本文的目标函数即为空调系统制冰与供冷的日运行费用，约束条件为冰蓄冷空调的机组供冷能力、蓄冰槽融冰能力等。

3.1.1 系统优化数学模型

设建筑在k时刻的空调负荷为qk，其中制冷主机承担qrk，主机运行费用为R(qrk)，蓄冰槽承担qik，其运行费用为I(qik)，全天运行费用M为：

优化控制的数学模型为：

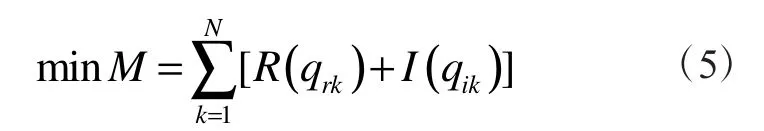
约束条件为：

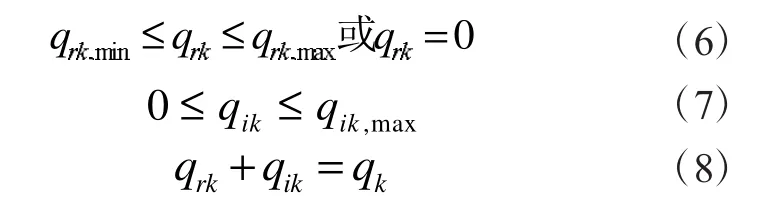
式中：qrk,max和qrk,min为主机k时刻的最大和最小供冷能力，kW；qik,max为蓄冰槽在k时刻最大供冷能力，kW。N为空调每天的供冷运行时间，h。

3.1.2 融冰性能曲线

因为在上述约束条件包含了蓄冰装置在k时刻的单位时间供冷量最大值，所以必须确定蓄冰装置的性能曲线才能求解上述问题。

本项目共有19台BAC蓄冰盘管，系统潜热有效蓄冰量为41472 kWh。根据文献[6]采用的经验公式，拟合内融冰的蓄冰槽k时刻最大融冰速率为：

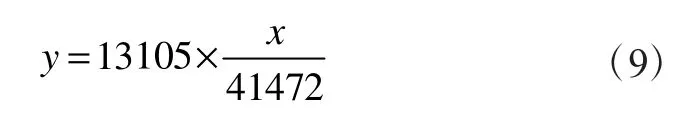
式中：y为t时刻最大融冰速率，kWh；x为蓄冰槽内剩余冰量，kWh。

3.1.3 主机性能曲线

本工程选用四台YS-HP蓄冷机组，制冷量为2896 kW，制冷工况功率550 kW，制冰量1912 kW，制冰工况功率494 kW。根据《约克冰蓄冷设计手册》中该型号机组的部分负荷性能曲线进行了拟合，拟合的公式为：

式中：PLR为负荷百分数，即冷机实际制冷量与额定制冷量的比值；COP为部分负荷下机组能效。

3.2 冷量分配优化

3.2.1 前提与假设

本文对于冰蓄冷空调的优化研究主要在于运行部分，即按照项目现有的设备以及型号对冰蓄冷系统进行优化。在此基础上，为了简化目标函数与约束条件的数学模型，采用以下前提与假设。

1）冰蓄冷空调系统的用能设备主要有双工况制冷机组，水泵和冷却塔，假设水泵，冷却塔和双工况制冷机组的运行情况是一一对应关系，故而只考虑双工况制冷机组的运行费用。

2）冷机在空调工况和蓄冰工况具有了相同的部分负荷性能曲线，忽略冷却侧对于双工况制冷机组的影响。

3）同一时刻开启的机组，每台承担的负荷相等。

4）蓄冰槽保温性能良好，不考虑冷量损失。

5）建筑工作时间为 8∶00～18∶00，空调仅在此阶段为建筑供冷，其余时间假定建筑无需供冷。

6）淮安采用两段制电价，其中，8∶00～24∶00 为电力峰段，电价为 0.882 元 /kWh；0∶00～8∶00 为电力谷段，电价为0.394元/kWh。

3.2.2 案例分析

采用某日本项目实测逐时负荷作为分析基础，负荷变化情况如图7所示。使用MATLAB中约束最小值优化（Constrained minimization）指令求解某日冰蓄冷系统的经济最优控制方案。

图7 典型日负荷变化

只需要在MATLAB中导入控制实施日空调逐时负荷，电价变化，双工况制冷机组部分负荷特性曲线以及蓄冰槽释冷曲线，即可计算出当天冷量分配策略和运行费用。

分别计算主机优先，融冰优先和经济最优控制三种运行方式冷量分配和日运行费用。

主机优先的控制方式也是本项目目前所采用的控制方式，其特点是运行稳定，控制简单可靠。在标准日负荷情况下，使用主机优先控制方式的冰蓄冷空调系统日运行费用为20407元，运行费用最多，没有突出冰蓄冷系统经济的优势。如图8所示。

图8 主机优先控制

采用融冰优先的控制方式，在标准日负荷情况下，空调日运行费用18694元，费用较少，蓄冰装置利用充分。如图9所示。

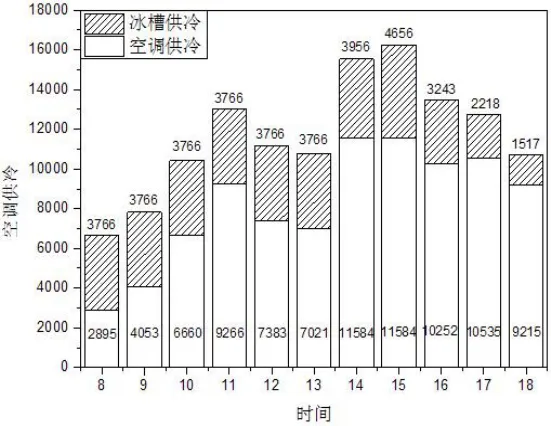
图9 融冰优先控制

采用经济最优的控制方式，在标准日负荷情况下，空调日运行费用18531元，费用最少，蓄冰装置利用充分。且经过优化分配，基本杜绝了后期系统供冷量不足的现象。如图10所示。

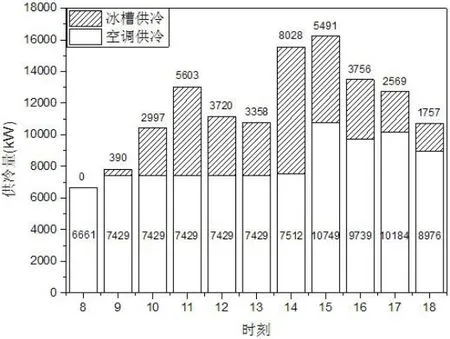
图10 经济最优控制方式

图11为不同控制方式下，单台机组COP的变化情况。可以很明显的看出，采用经济最优控制方式运行的机组COP始终保持在较高状态，而融冰优先和主机优先控制方式下的制冷机组，COP波动较大，且普遍低于经济最优控制方式。这也正是在峰值电价相同的情况下，经济最优的控制方式能够节约运行费用的原因。

图11 单台机组COP变化情况

3.2.3 经济性比较

上述方法，分别模拟25%，50%和75%典型日负荷下三种调节方式的冷量分配情况，可得不同典型日负荷率下三种运行方式单位冷量价格，如图12所示。

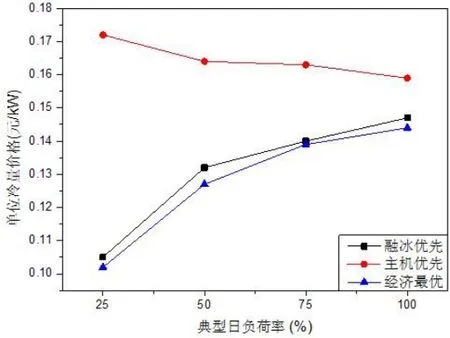
图12 单位冷量价格随日负荷率变化趋势

由图12可知，在主机优先控制方式下，冰蓄冷空调系统单位冷量价格随着典型日负荷的增大而降低。相反，融冰优先和经济最优控制方式下，冰蓄冷空调系统单位冷量价格随着典型日负荷的增大而升高。经济最优运行方式在任何情况下，运行费用始终保持最低。随着典型日负荷率的增大，三种控制方式下的单位冷量价格差距越来越小，逐渐靠近。

为了更加详细地研究空调负荷对供冷价格的影响，将日负荷细化至逐时负荷，计算结果如图13所示。

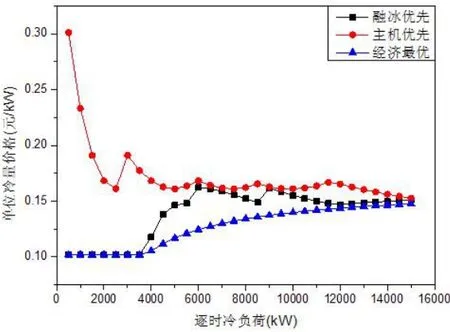
图13 单位冷量价格随逐时负荷变化趋势

由图13可知，主机优先控制方式下系统供冷价格始终保持最高，随着逐时冷负荷增大而减小。之所以会发生这种现象，是因为逐时负荷低时，主机优先控制方式优先使用制冷机组，且此时制冷机组的负载率和COP很低，加之白天机组运行时为峰值电价，因此此时主机运行费用较高。但随着逐时负荷的提高，制冷机组的负载率随之提高，使得机组一直在较高能效范围内工作，造成供冷价格持续下降。当冷负荷进一步提高，机组满负荷运行，系统开始使用价格更低廉的蓄冰槽内的冷量，造成供冷价格再一次下降，最终趋向于其他两种供冷方式的价格。

融冰优先控制的价格趋势与主机优先方式相反，因为这种方式先使用价格低廉的蓄冰槽内冷量，此时系统运行费用最低。当蓄冰槽供冷速率无法满足建筑冷负荷时，机组开启，供冷价格用迅速提高。此时机组的供冷价格与主机优先供冷变化趋势相同，都是随着负荷的增加而降低。因此造成融冰优先控制方式的供冷价格升降反复，最终趋于稳定。

与前两种控制方式不同，经济最优控制方式的供冷价格曲线并非固定不变，但为了定性分析，设定经济最优控制方式蓄冰槽供冷速率与融冰供冷相同，机组COP为不同典型负荷率的平均值5.417。经济最优控制在较低范围时，使用蓄冰槽内的冷量，供冷价格最低。超出此范围后，制冷机组开启导致供冷价格有所提高。相比于融冰供冷方式而言，因为经济最优控制首先已在上位机优化了负荷分配，虽然都是运行制冷机组，但是经济最优控制下的机组COP普遍高于融冰优先。当负荷变大时，三种控制方式单位冷量供冷价格差距变小，逐渐趋于一致。

综上所述，在融冰供冷基础上，系统在低负荷阶段运行时间，决定了经济最优控制最终能比其他两种控制方式节约的运行费用。

4 结论

1）以6组输入和1组输出模式下的BP神经网络预测建筑负荷，研究发现具有1个或2个隐含层的神经网络预测结果远远高于更多层数的预测结果。

2）BP神经网络有可能产生极个别偏差较大的预测负荷，若以此预测负荷作为优化控制的依据，将不能体现控制的经济性甚至会影响后期系统供冷不足的情况。为了避免这种情况，本文提出多次预测取平均值的方法，结果表明该方法的指标评估结果要远远优于指标平均的结果。

3）以经济最优为控制目标，主机动态能效和蓄冰装置融冰曲线为约束条件，通过MATLAB优化冷量分配的控制策略合理可行，可以大大节省冰蓄冷空调系统的运行费用，具有一定的实用价值。

4）通过比较不同负荷下三种供冷方式的单位冷量价格变化趋势可知，经济最优控制方式节约运行费用，主要集中于较低负荷时，机组负载率较低的时段。