狭长空间中部排风系统阻抗模拟及实验分析

谢玉良 张旭叶蔚 邰彦寰

同济大学机械与能源工程学院

狭长的空间中很难准确测量通风量，如飞机客舱、火车车厢、隧道等。由于狭长空间的横截面小、纵向距离长的特点，房间的气流组织难以直接得出，对于狭长空间中排热排污等问题所需的排风量也难以确定，若是排风量计算不足，则直接威胁到内部人员和设备的安全。当前文献中对此研究较少，一般采用CFD模拟计算并通过相似原理进行模型试验的验证[1]。Chao[2]等人提出了一种与遗传算法相结合的多区技术改进的示踪气体浓度衰减法来确定狭长空间的通风率。杨立军[3]等人通过绘制并联风机性能曲线分析了不同条件下对并联风机运行特性的影响，通过引入集群因子，得到轴流风机群的性能曲线，阻力特性和空冷系统的工作点。王峰[4]等人基于不可压缩粘性流体湍流模型，采用CFD方法对曲线隧道通风沿程阻力损失进行模拟计算。论证了曲线隧道断面形式和通风速度与沿程阻力系数之间的关系。梁彦超[5]利用SC/Tetra软件对集装箱船机舱内狭长空间空气流动进行数值计算和模拟，获得整个机舱的速度场和温度场分布，针对性的提出了通风系统布置的优化方案。Bredell[6]等人FLUENT模拟，研究了风机入口流场变化时对并联风机群性能的影响，并且对比了两种不同类型风机的性能。Duvenhage[7]等人利用CFD数值模拟考虑了纵向轴（长轴）风对并联风机性能的影响。刘广强[8]等人利用CFD方法对不同环量指数所设计的风机进行模拟对比。通过对现有风机进行数据实测验证物理模型的正确性。本文将狭长空间的通风问题简化成通风管网的水力计算，通过得出风机与管路匹配的工作点来计算所需要开启的风机数量。

1 狭长空间排风问题的简化分析

1.1 狭长空间的简化分析

本文的研究对象为特殊实验目的的隧道型狭长空间，内部构造较为复杂，简化模型如图1所示，其中AB段长 76 m，宽 18 m，高 9.2 m，BC段长 82 m，宽18 m，高5.2 m。A端为开敞端，中部B处设有两边对称布置的离心排风机8台风量140000 m3/h，全压935 Pa，C端设有6台对称布置的6台轴流送风机，风量 60000 m3/h，全压 635 Pa。

图1 狭长空间排风模型

对此研究对象进行分析后，进行如下简化，如图2所示。即简化为一定长度的通风管道，左端自由流动、中部机械排风、右端机械进风的流体管网问题。同时做如下假设：所有相同管道横截面积相等，故流量比等于速度比。

图2 简化通风模型

对图2进行简要分析：

1）令 a、b、c三点（断面）连接为大气环境，即 a、b、c三点静压Psa=Psb=Psc=0。同时令A、B、C三个断面均紧邻a、b、c三个断面。其中A、B两个断面分别在风机之前和之后。此外，令b点的坐标为0，a点和c点的坐标分别为l1和l2。

2）因为a处风机为送风机，A断面静压PsA＞0、动压为。同时，因b处风机为排风机，B断面静压 PsB＜0、动压为。

1.2 风机并联特性

以某公司生产的T4-72XX型离心风机为例，根据样本给出的风机特性曲线的典型工况点，通过最小二乘拟合得到风机特性曲线公式。采用多项式的形式表示风机增压△P和空气流量Q的关系式[3]：

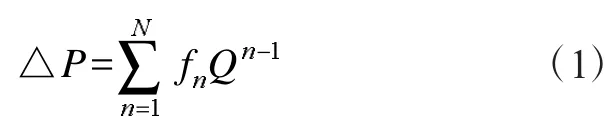
式中：fn为多项式系数；△P风机增压，Pa；Q风机流量，m3/s。

管网系统的阻力特性曲线通常为二次抛物线，对于本文的简化模型，管网的压降△Ps和流量Qs的关系式为：

式中：S为管道综合阻力系数，kg/m7。

对于单台风机及其与外部管网组成的系统，风机性能曲线与管网阻力特性曲线的交点，即为风机工作点。当多台性能相同的风机并联运行时，风机系统的全压不变，流量累加，即在相同的全压情况，流量变成原来单台风机的多倍。而外部管网的阻力特性不发生变化。对于T4-72XX型离心风机拟合的性能曲线系数如表 1（R2=0.9987）：

2 狭长空间阻力系数的影响

2.1 几何建模及网格划分

研究对象是狭长空间内风机启停工况下排风效果的问题，故模型模拟的区域为包括送排风机在内的整个区域。几何模型按照某狭长空间实际尺寸建立，利用商业CFD软件进行三维模型的建立及网格划分。采用的四面体网格，并对送、排风机及开敞端进行局部加密处理。

2.2 边界条件

入口及出口：将机械进排风的入口及出口进行适当简化，C处机械送风按照压力入口进行设置，需确定全压大小，入口方向，总温以及湍流参数情况。本次模拟主要查看下场空间内流场的分布，则空气入口温度的设定对模拟的结果没有影响，可将其设为与外界温度一致。B处机械排风按照压力出口设置，需要确定出口处静压。A处敞开口按照压力入口设置，出口静压为0 Pa。

湍流模型使用对流线曲率大，有漩涡和旋转的内部流场的模拟更加适用的RNG k－ε湍流模型，使用Scalable壁面函数。计算方法：计算过程中采用亚松弛因子，Coupled算法，在动量方程，k方程和ε方程选项中均采用二阶迎风格式。

2.3 结果分析

Case1：将送风机C关闭，仅设置成压力入口，表压P=0 Pa。图2的通风模型即可简化为两端自然进风，中部排风的三通模型。收敛后各进排风口风量如下：Qa=242.35 m3/s，Qc=10.33 m3/s，Qb=-252.65 m3/s。

由管网并联计算公式：

联立式（3）～（5），解出管网系统阻力系数S=0.0148 kg/m7。改变排风机全压后，不同全压下对应的个排风口风量不同，但管网系统阻力系数S的计算误差＜1%，认为本次实验中阻力数S计算正确。

Case2：按实际中狭长空间标准工况下，B处排风机及C处送风机全部开启，设B处压力出口全压P=-945Pa，C处压力入口全压P=635Pa，A处压力入口P=0 Pa。收敛后各进排风口风量如下：Qa=156.02 m3/s，Qc=96.95 m3/s，Qb=-252.74 m3/s。

对比Case1和Case2结论：

1）两次计算并联管道阻力系数S的误差＜1%，认为S计算正确，因此管网系统阻力方程为：

2）总排风量仅取决于B处离心排风机，C出送风机的工况不能改变总排风量，仅能改变并联管段AB、AC流量分配比。

3）当前工况B出口单离心风机风量11.37万m3/h，与理论风量14万m3/h对比减少了17.76%；C处单台风机风量5.81万m3/h，与理论风量6万m3/h对比减少了3.1%。

由结论可知实际工况下相同风机并联后风量不会出现多台风机风量相叠加的情况，而是有一定损失。B处单台离心排风机模拟风量与理论相比减少2.63万m3/h。根据case2模拟结果，考虑B处离心风机并联损失，即可得到8台离心风机并联的性能曲线，离心风机拟合的性能曲线系数如表2（R2=0.9987）：

即，模拟风机性能曲线为

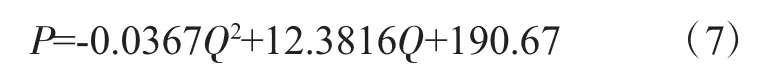
联立式（6）和（7），即可得到风机性能曲线与管路性能曲线的焦点为该工况下风机工作点，如图3所示。图中工作点的坐标为 （907818 m3/h，941.2 Pa），与Case2中模拟得到的风量90.96万m3/h相比误差为0.2%。

图3 并联性能曲线与工作点

当狭长空间系统阻力改变时，管网阻力系数S将增大。通过对图1狭长空间AB段和BC段分别增加一定数量的车辆时，得到的并联性能曲线与工作点如图4所示。其中系统阻力特性Ⅲ与风机性能曲线Ⅳ的交点是图3所述的工况。曲线Ⅱ与风机性能曲线Ⅳ的交点是狭长空间AB段增加一台大车、BC段增加两台小车时的工作点。曲线Ⅰ与风机性能曲线Ⅳ的交点是狭长空间AB段增加两台大车、BC段增加四台小车时的工作点。大车的长宽高分别为29.2 m、7.5 m、6.9 m，小车的长宽高分别为9.5 m、3.4 m、2.3 m。图4中工作点 B 的坐标为（889682 m3/h，1009.3 Pa），工作点 B 的坐标为（836823 m3/h，1085.8 Pa）。

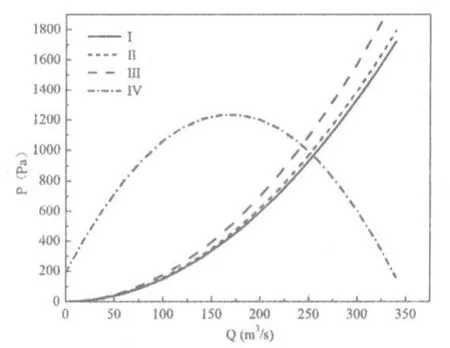
图4 管网变化后并联性能曲线与工作点

利用阻塞比来分析上图中Ⅰ、Ⅱ、Ⅲ的工况，阻塞比即实验模型在实验风道截面上的投影面积与风道截面积之比。拟合得到管道阻力系数S与管段阻塞比的关系式 S=f(β)，拟合系数如表 3（R2=1）。

即管道阻力系数与阻塞比的关系式为：

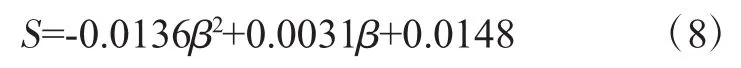
式中：S为管道综合阻力系数，kg/m7；β为管道阻塞比。

式（8）表明，在当前并联管段中，管道阻力系数S与管道阻塞比β近似成平方关系，且随着阻塞比的增加而增大。

3 中部排风模型实验

3.1 实验系统

为了更准确确定不同工况下狭长空间中部排风系统排除污染物所需要的时间，本文通过模型实验来验证，定常粘性流体的量纲关系式可以简化为：

原型和模型试验中很难保证同时满足上述4个准则数。欧拉（Eu）是待定准则并且是弗劳德（Fr）准则和雷诺（Re）准则的函数，本文研究对象为等温定常流动，忽略弗劳德（Fr）准则数模型与原型的流动介质是空气，则认为（Pr）准则数相等，因此考虑雷诺（Re）准则数。根据文献[9-10]中关于狭长空间多源汇合温度扩散的模型实验研究，本实验选取的几何缩尺为1∶13，风速比例尺为 1∶1.82。AB 断面尺寸为 1.4 m×0.8 m，BC断面尺寸为1.4 m×0.4 m，模型中AB和BC两段的Re数分别为4.32×104和2.49×104，模型已进入自动模型区。

图5 模型送风系统

实验台包括送风、排风风机，风管，变频器，CO2发烟机以及测试仪器。测试仪器包括风速仪、CO2浓度测量仪、微压计等。送风机型号为4-72-2.8A，风量1131～2356 m3/h，风压 606～994 Pa，转速 2900 r/min，功率1.5 kW；排风机型号为4-72-NO3.6A，风量2664～5268 m3/h，风压 989～1578 Pa，转速 2900 r/min，功率3 kW。分别由1.5 kW和3.7 kW的变频器控制。送风口尺寸为70 cm×15 cm，排风口尺寸为15 cm×15 cm。模型实验现场图如图5、6所示。

图6 模型排风系统

3.2 实验结果分析

CO2气体示踪实验中所用工况都为AB段中1台大车，BC段两台小车，共有关闭、开启射流风机两种工况，每种工况有4组实验，射流风机布置在BC中间，风量2中部排风机对应开启8、7、6、4台，模型实验对 应 排 风 量 为 4140 m3/h、3623 m3/h、3105 m3/h、2070 m3/h，对应工况编号为 A-1、B-1、C-1、D-1，开启射流风机时对应的实验编号为 A-2、B-2、C-2、D-2。CO2浓度测量仪记录间隔为10 s，图7显示了不同中部风机排风量下排风口处CO2气体浓度变化。图8显示了开启射流风机时不同中部风机排风量下排风口CO2气体浓度变化。CO2气体从0s开始在C断面释放，150 s时停止。

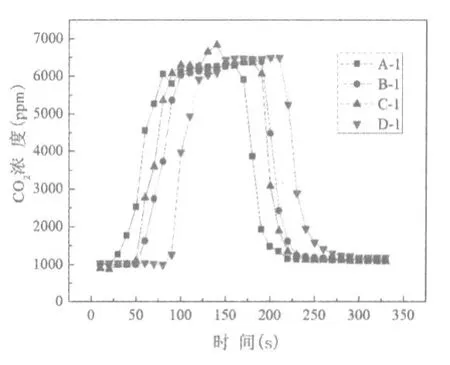
图7 排风口处CO2气体浓度变化

从图7中可以看出：1）每条曲线均有陡峭上升阶段，缓慢增长阶段，加速下降阶段和缓慢下降阶段。2）中部风机排风量的不同会导致CO2浓度变化有响应的提前或滞后，A-1与D-1相比中部排风量增加一倍，CO2浓度升到最高值的时间和降低至环境值的时间都提前约40 s。3）各工况最高CO2浓度基本相同，都在6000 ppm左右。

从图8中可以看出：1）开启射流风机时中部排风口CO2浓度达到峰值时间比不开启时减少20 s。2）除A-2工况外其余工况CO2浓度最高值变化不大。

图8 增加射流风机后排风口处CO2气体浓度变化

4 结论

针对某狭长空间横截面小、纵向距离长的特点，空间的气流组织难以利用流体管网方式得出，文章通过对房间阻力系数的模拟，得出如下结论。

1）管网性能曲线与拟合风机性能曲线的交点即风机工作点与数值模拟得出的工况点误差为1%，本方法有一定可行性。两段式中部机械排风系统中，若一端为自由端，另一端自由或加机械送风，则总排风量仅取决于中部排风机状态，机械送风端风机变化不能改变总排风量，仅能改变两管段流量分配比。在当前并联管段中，管道阻力系数S与管道阻塞比β近似成平方关系，且随着阻塞比的增加而增大。

2）通过CO2气体示踪实验得出在当前模型下，排除CO2所需要时间为200 s，当开启射流风机时所需要时间为180 s。