土壤铜污染光谱特征波段分析、界限浓度划分及含量预测

付萍杰，杨可明

中国矿业大学（北京）/煤炭资源与安全开采国家重点实验室，北京 100083

土壤污染问题一直备受关注，被认为是对人类健康构成潜在风险的全球性问题。重金属以不同的形式和浓度聚集在土壤中，因此对土壤中重金属元素进行监测是很有必要的。众多学者采取野外采样和室内化学分析的方法研究土壤中重金属的种类和含量以及它们之间的相互关系，得出的结果精度高、准确性强，但是，该方法费时费力费钱，很难获取大面积的污染监测结果（李湘洲，2000；吴健生等，2011；肖捷颖等，2013）。

由于有机质、粘土矿物、铁氧化物等在光谱曲线中具有一定的吸收特征，并对重金属具有一定的吸附作用，借助土壤中不同的重金属含量之间及其与有机质、粘土矿物、铁氧化物等之间的关系（李巨宝等，2005；焦文涛等，2005；李娜等，2010；龚绍琦等，2010；南聪强等，2012），预测土壤重金属已成为了常用手段，也取得了一定的实质性成果，间接地预测了土壤重金属含量，实现了无光谱特征的土壤重金属含量的监测。Stazi et al.（2014）研究发现，土壤中 As的含量与土壤光谱曲线在580、660、715、780 nm波段处的吸收峰相关性较高，可以用来预测土壤中As的含量。Gholizadeh et al.（2015）利用光谱数据研究煤矿周围的土壤重金属污染，研究发现，Pb含量与513 nm波段处的光谱反射率具有较高的相关性，Zn含量与769 nm波段处的光谱反射率具有较高的相关性，土壤光谱曲线在一阶导数处理后，位于450～550 nm、1400 nm、1900～2000 nm、2200 nm波段处的光谱特征明显。Stenberg et al.（2010）发现对土壤光谱数据进行一阶导数、二阶导数处理有助于研究土壤特征。Xia et al.（2007）利用光谱曲线研究长江流域土壤中 Cd污染情况，发现560～760 nm波段处土壤光谱反射率一阶导数与土壤中Cd含量相关性较高，可以用来预测Cd的含量，粘土矿物在1400、1900、2200 nm波段处（吸收峰）光谱反射率一阶导数值与Cd含量具有较高的相关性，可以用来预测 Cd含量。总体而言，已有研究取得的成果大体分为以下三类：570～830 nm 光谱波段区间内土壤有机质含量与反射率之间有较强的相关性，有机质含量越低，土壤反射率越高；铁氧化物在400～1300 nm波段区间内因具有吸收特征，可用于探测重金属含量，铁含量越高，土壤反射率越高，土壤中铁的含量与重金属含量具有一定的相关性；粘土矿物在2200 nm附近具有明显的吸收特征，根据吸收峰深度可预测重金属含量。

随着土壤重金属含量与光谱曲线之间关系研究的深入，众多学者在土壤重金属含量预测模型的建立中也取得了大量的成果，利用支持向量机（Stazi et al.，2014），多重线性回归，人工神经网络法（Kemper et al.，2002），倒数对数、一阶微分（王维等，2011），一阶导数、包络线去除（任红艳等，2009）处理后的光谱曲线特征波段吸收峰深度与重金属含量、有机质含量、铁含量之间的关系预测重金属含量，预测模型精度较高，但均方根误差也较大。同时，多变量预测模型也取得了一定的成果，用偏最小二乘法（Kooistra et al.，2001；Yeniay et al.，2002；Maliki et al.，2014；Stazi et al.，2014；Rathod et al.，2015；Gholizadeh et al.，2015），最大、最小一阶导数比值，多元线性回归分析，多元自适性回归样条法（Kooistra et al.，2001；Wu et al.，2005a；Pandit et al.，2010），主成分分析法（Maliki et al.，2012）预测重金属含量，预测模型精度较高，且均方根误差较小，模型建立较成功。因此，土壤重金属含量预测模型研究结果显示，采用多变量预测重金属含量模型精度明显高于单变量预测模型精度。

本研究利用土壤铜（Cu）污染538～834 nm波段区间的光谱数据及一阶导数距离检测土壤Cu污染的界限浓度及光谱特征波段区间，并根据界限浓度、多重分形谱参量、一阶导数距离参量、土壤含水率及有机质含量等建立土壤Cu浓度的预测模型，为土壤重金属污染的高光谱研究提供依据，精确土壤重金属污染光谱的研究范围，为利用界限浓度建立土壤重金属浓度预测模型提供新思路，促进高光谱技术在土壤重金属污染检测中的应用。

1 材料与实验设计

本研究设计的土壤 Cu污染试验，采用CuSO4∙5H2O 分析纯制备重金属污染土壤，添加量分别为 0、50、100、150、200、300、400、600、800、1000、1200 μg∙g-1。每种污染梯度平行设置 3组处理，共33个土壤样品，选用自然土进行实验。自然土于2017年5月采自北京市海淀区一片废弃的土地，自然土样品Cu本底值为19.6 μg∙g-1，其土壤含水率为 20.588%～35.484%，有机质含量为10.40～21.80 g∙kg-1。对土壤的处理分以下几步，（1）土壤预处理，土壤先过5 mm筛，然后过2 mm筛，将过筛之后的土壤混合均匀。（2）称取等量（5 kg）的土壤和不同添加量的CuSO4∙5H2O混合，使用搅拌棒将混有CuSO4∙5H2O的土壤搅拌均匀。（3）将土壤静置1 d后，第二天上午10:00使用电子秤和直径为10 cm的圆柱形模具称取等量的不同Cu污染水平的土壤样品，后于11:00—14：00使用光谱范围为340～2500 nm的SVC HR-1024I高性能地物光谱仪采集土壤样品光谱。（4）测定土壤含水率、土壤中有机质和Cu含量，土壤含水率测量方法为取土烘干法（徐倩等，2017；颜小飞等，2017）；土壤中有机质与Cu含量的测量方法为电感耦合等离子体发射光谱法（曹洪斌等，2016；梁榕源，2018），测量仪器为 ICP—OES电感耦合等离子发射光谱仪。

2 研究方法

2.1 经验模态分解

经验模态分解（Empirical Mode Decomposition，EMD）的目的是通过对非线性、非平稳信号的分解获得一系列表征信号特征时间尺度的本征模函数IMF（Intrinsic Mode Function），使得如系列IMF1，IMF2，IMF3，……，IMFn等各个IMF是单分量的幅值或频率调制信号。EMD基本思想是：将 1个频率不规则的波（原形波，PW）转化为多个单一频率的波加上余波（res）的形式，即 PW=ΣIMFn+res。EMD降噪的主要思想是通过一定准则找出模态函数中的“无用”成分，无用的IMF被认定为噪声，予以剔除（黄海等，2007；谭善文等，2004；胡劲松等，2007）。该去噪过程是自适应的，能够自主分解输入的信号，不需要先验知识，故相对傅里叶变换和小波去噪而言具有明显的优势（王维强等，2012）。

经验模态分解（EMD）对原始信号 X(t)处理后可获得多个本征模函数（IMF），EMD分解出来的各 IMF分量包含了 X(t)的不同时间尺度的局部特征。一个 IMF分量需满足两个条件：（1）IMF分量中过零点和极值点的数目要相等或者最多相差1个；（2）IMF分量上任意一点由局部极大、极小值点确定的包络线的均值为零，即t关于t轴局部对称。

假设X(t)为一条复杂的原始光谱曲线，则EMD的处理过程为：（1）找出X(t)所有的极大值点和极小值点，并用三次样条插值函数拟合形成原光谱曲线的上、下包络线；然后计算该上、下包络线的均值（记作曲线m）；再根据h=X(t)-m得到1条新的曲线h。如果h不满足IMF的两个条件，则需重复上述步骤，直到分解出第一个分量 IMF1；（2）以X(t)减去IMF1得到第一阶剩余光谱 r1，把r1作为新的原光谱曲线，重复步骤（1），得到IMF2与r2；以此类推，可得出IMF3与r3，……，IMFn与rn，当rn变为一个单调函数时，筛选结束。

2.2 多重分形理论

多重分形是描述在不规则的分形空间之上质量分布的定量化工具，多重分形谱是描述多重分形的一套常用参量。就光谱信息而言，光谱信号在多重分形时，不仅需要考虑把整个光谱区间分成不同的小区域（也即能覆盖整个光谱的不同盒子，小区域个数就是盒子的数目），还要考虑每个盒子中信号的质量（盒子内所有光谱反射率之和）及到各个盒子之间光谱信号的差别。以α表示光谱信号中某个盒子的分维（也称奇异指数或标度指数），具有相同α的盒子构成了一个分形子集，则一个多重分形就可以看成是具有不同α的分形子集的并集。把具有相同 α的盒子分布概率信息称为多重分形谱f(α)，α和f(α)能够表述多重分形的局部特征，反映光谱信号的微小差异。Δα表示多重分形谱宽度，反映了整个分形结构上光谱信号的概率测度 Pi(δ)的分布不均匀程度，Δf(α)表示最大、最小概率 Pi(δ)子集分形维数差。多重分形谱计算步骤如下：

（1）概率测度。若定义Si(δ)为当盒子尺寸为δ时第i个小盒子的质量，则第i个小盒子内质量的分布概率即为概率测度Pi(δ)，可表示为：

式中，ΣSi(δ)是全部光谱反射率值之和。

（2）配分函数。对概率测度 Pi(δ)用 q次方(-∞＜q＜+∞，q为权重因子)进行加权求和，即为配分函数Xq(δ)。对于多重分形分布概率测度，配分函数Xq(δ)和盒子尺寸 δ之间需满足 Xq(δ)∝δτ(q)，其中，τ(q)为质量指数，则配分函数Xq(δ)可表示为：

如果上式成立，即Xq(δ)和盒子尺寸δ存在幂函数关系，则 logXq(δ)～logδ的斜率即为质量指数 τ(q)。

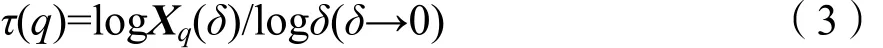
（3）计算τ(q)与q的关系。对每个q值，利用

式（3）在双对数坐标系中采用最小二乘法拟合估算τ(q)，得到τ(q)与q的关系。

（4）求多重分形谱。多重分形谱f(α)是指不同的奇异性标度指数α的分形子集所确定的分形维数。在无标度区间内，概率测度Pi(δ)与盒子尺寸δ的划分需满足下面的幂函数子集 Pi(δ)∝δα，α 由τ(q)曲线的Legendre变换来决定，即α=dτ(q)/dq，因此：

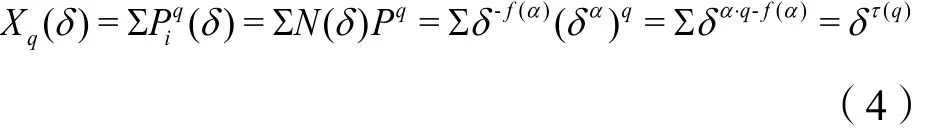
式中，N(δ)为具有奇异性标度指数为α的子集的个数；N(δ)与 δ之间具有幂函数关系 N(δ)=∝δ-f(α)，f(α)为具有奇异性指数α的分形子集的分形维数。

当光谱曲线满足多重分形特征时，Σδα·q-f(α)-τ(q)=1，当 δ→0 时，得到多重分形谱，即 f(α)与α的关系曲线。

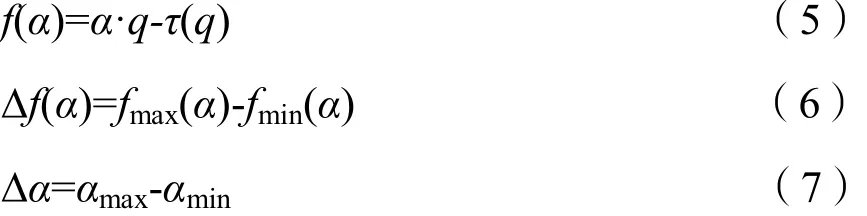
2.3 一阶导数距离

光谱曲线一阶导数可以表示该曲线在某一点的斜率（变化率），其计算公式为：

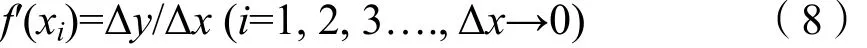
式中，xi为光谱曲线第i个反射率对应的波长；f′(xi)为xi波长处光谱反射率一阶导数

将光谱曲线一阶导数距离定义为两条波长范围相同、波长间隔相同的光谱曲线一阶导数差值的绝对值，其计算公式如下：

式中，f′(xi)为一条光谱曲线 xi波长处光谱反射率一阶导数；g′(xi)为另一条光谱曲线xi波长处光谱反射率一阶导数。

选取一组极为相似的光谱曲线中的一条光谱曲线为基准光谱曲线，可以得到该组中剩余的每条光谱曲线与基准光谱曲线的一阶导数距离，通过一阶导数距离变换可以放大两条相似光谱曲线之间的差异，更有利于鉴别两条光谱曲线之间细微的差异。

2.4 数据处理

SVC HR-1024I高性能地物光谱仪采集的土壤样品光谱数据在不同的波段区间内其分辨率是不同的，350～1000、1000～1850、1850～2500 nm 波段区间内分辨率分别为 3.5、9.5、6.5 nm。使用sigProcessor将数据重采样到1 nm精度，并导出为“. xlsx”格式。以不同Cu污染水平下538～834 nm波段区间内土壤光谱为研究对象，利用 MATLAB对其进行一阶导数处理，并求其一阶导数距离。利用MATLAB软件，通过经验模态分解（EMD）去除不同 Cu污染水平下整个土壤光谱波段范围内（343.1～2052.1 nm）的噪声，再分析其多重分形特征，得到多重分形谱参量。

3 土壤铜污染光谱界限浓度及土壤铜含量预测

3.1 土壤Cu污染光谱界限浓度划分

3.1.1 土壤Cu污染光谱一阶导数

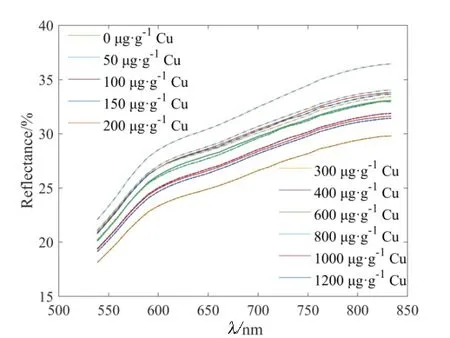
图1 不同Cu污染水平下538～834 nm土壤光谱反射率Fig. 1 Soil spectral reflectivity at 538～834 nm band interval under different Cu pollution level

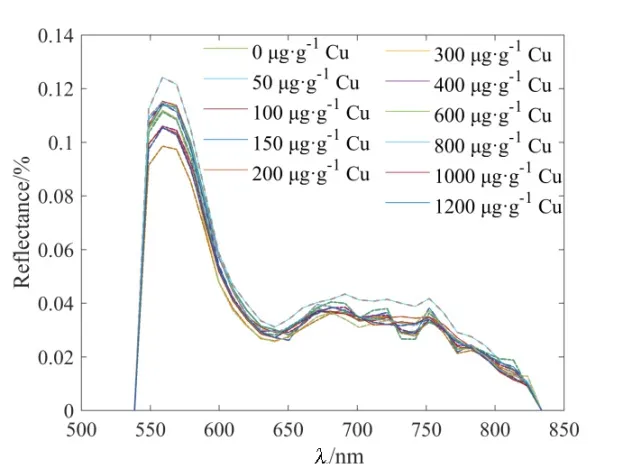
图2 不同Cu污染水平下538～834 nm土壤光谱反射率一阶导数Fig. 2 First-order derivative at 538～834 nm band interval of the soil’s spectral reflectivity under different Cu pollution level

由图1可知，0～1200 μg∙g-1Cu污染下538～834 nm波段区间内土壤光谱反射率与处理水平之间关系不明确（图1）。分析其一阶导数可得50～150 μg∙g-1Cu污染下土壤光谱反射率一阶导数的最大值大于 CK污染下土壤样品光谱反射率一阶导数最大值（图 2），200～1200 μg∙g-1Cu 污染下土壤光谱反射率一阶导数的最大值基本上小于 CK污染下土壤样品光谱反射率一阶导数最大值，但是局部现象不明显。

根据光谱曲线一阶导数距离计算公式，以 CK污染下土壤样品光谱曲线为基准曲线，将50～1200 μg∙g-1Cu污染下土壤光谱曲线一阶导数距离定义为任一 Cu污染水平下土壤光谱曲线一阶导数与 CK处理下土壤光谱曲线一阶导数差值的绝对值。利用式（8）和式（9）可得以CK处理为基准光谱曲线的不同Cu污染水平下土壤光谱曲线一阶导数距离（图3）。

图3 不同Cu污染水平下538～834 nm土壤光谱反射率一阶导数距离Fig. 3 First-order derivative distance at 538～834 nm band interval of the soil’s spectral reflectivity under different Cu pollution level

由图 3 可知，50～1200 μg∙g-1Cu 污染梯度下土壤光谱曲线特征区间可分为两类：50～150 μg∙g-1Cu（土壤样品Cu质量分数：60～120 μg∙g-1）污染梯度下土壤光谱曲线一阶导数距离最大值分布在730～760 nm 波段区间（见表 1），200～1200 μg∙g-1Cu（土壤样品 Cu 质量分数：160～740 μg∙g-1）污染梯度下土壤光谱曲线一阶导数距离最大值分布在540～590 nm 波段区间内（见表 1）。据此推断，120～160 μg∙g-1（150～200 μg∙g-1Cu 添加量）为土壤Cu污染的界限浓度（见表1）。

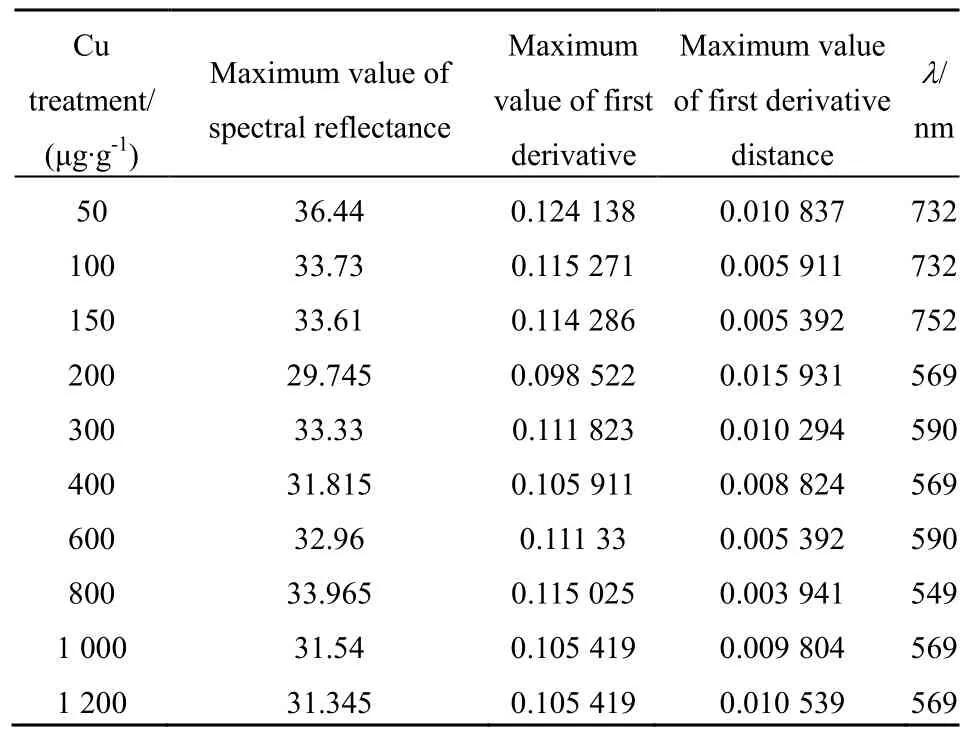
表1 不同Cu污染水平下538～834 nm土壤光谱曲线特征Table 1 Characteristics of 538～834 nm soil spectral curve under different Cu pollution level

3.1.2 土壤Cu污染光谱多重分形特征

3.1.2.1 土壤Cu污染光谱经验模态分解

为了避免整个波段区间上（波长范围 343.1～2052.1 nm）光谱噪声的影响，对数据进行去噪处理。依据本实验所采集到的不同处理水平Cu污染下土壤光谱数据，分别对33组数据：0 μg∙g-1Cu-1、0 μg∙g-1Cu-2、0 μg∙g-1Cu-3、……、1200 μg∙g-1Cu-1、1200 μg∙g-1Cu-2、1200 μg∙g-1Cu-3 污染梯度的土壤光谱进行EMD处理。由于光谱噪声成分主要集中在高频段的IMF分量上（赵雯雯等，2008），可通过剔除IMF1分量达到光谱有效降噪。又因为原始信号中最有效的信息往往集中在几个 IMF分量中（郭兴明等，2014），所以可利用剔除IMF1后的剩余IMF分量和余波进行光谱重构。基于上述光谱去噪和重构方法，可得到不同处理水平Cu污染梯度下土壤的重构光谱，如图4所示。

3.1.2.2 土壤Cu污染光谱多重分形特征

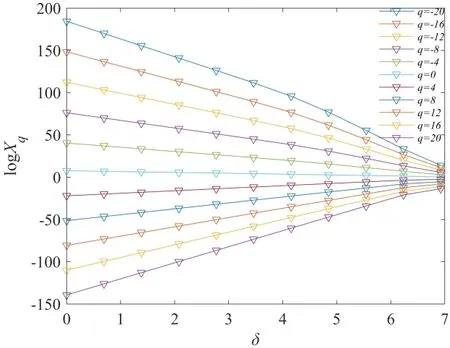
图5 50 μg∙g-1 Cu污染下土壤重构光谱logδ和logXq(δ)线性关系Fig. 5 Linear relationship of the soil’s reconstruction spectrum logδand logXq(δ) under 50 μg∙g-1 Cu pollution gradient

对每3组平行的Cu污染下的重构土壤光谱进行取均值，可得不同处理水平Cu污染下重构土壤光谱的平均光谱。采用多重分形理论的非线性信号处理和分析方法，可获取0～1200 μg∙g-1Cu污染梯度下土壤重构光谱的多重分形特征。根据式（2）和式（3）可得，当权重因子 q在-20～20之间取不同值时，以50 μg∙g-1Cu污染下土壤重构光谱的logδ和logXq(δ)之间的关系为例（见图5），图中线均保持较好的线性且汇聚于一点，因此土壤重构光谱曲线表现出良好的标度不变性；同时，logδ和logXq(δ)之间拟合所得直线斜率均不同，表明了50 μg∙g-1Cu污染下土壤重构光谱具有多重分形特征（Mandelbrot，1982；周炜星等，2000）。由图 6可知，质量指数τ(q)与q之间的线性拟合并不是一条标准直线，而是大体呈直线分布，表明50 μg∙g-1Cu污染下土壤重构光谱中出现了不同的奇异性。对CK和 100～1200 μg∙g-1Cu污染梯度下土壤重构光谱进行类似分析，所得结果相同，即土壤Cu污染重构光谱具有多重分形特征。

采用多重分形理论的非线性信号处理和分析方法，可获取0～1200 μg∙g-1Cu污染梯度下土壤重构光谱的多重分形特征。基于上述分析结合式（5）、

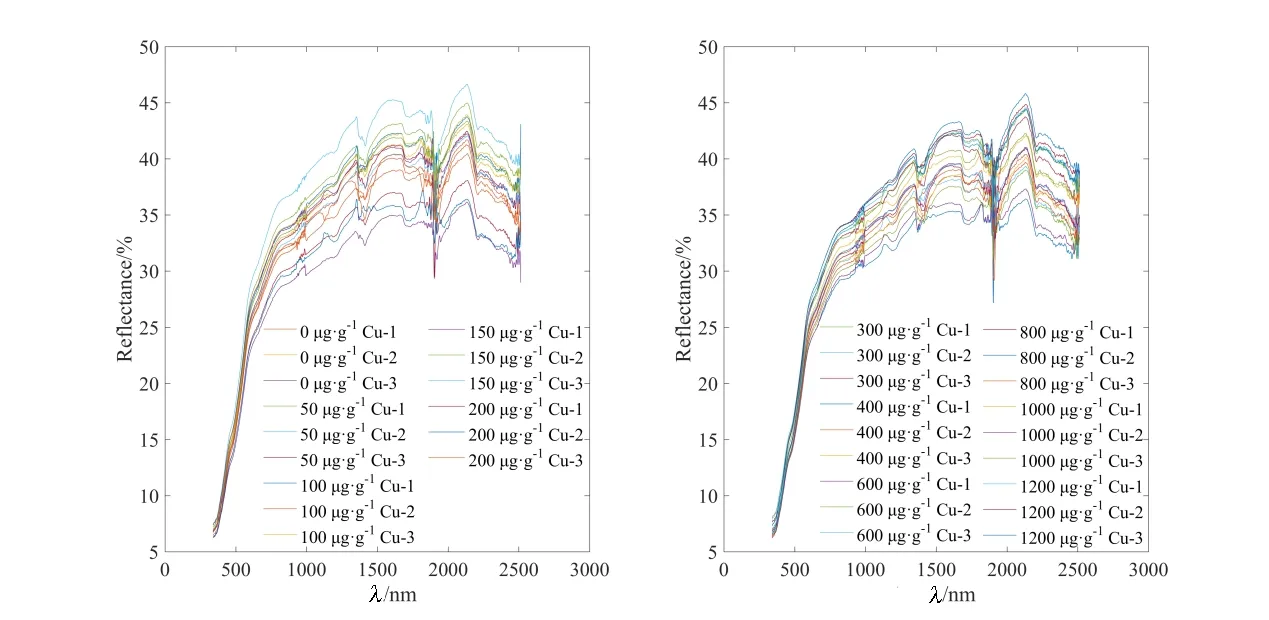
图4 不同Cu污染水平下土壤EMD重构光谱Fig. 4 EMD reconstruction of the soil spectrum under different Cu pollution level

表2 不同Cu污染水平梯度下土壤重构光谱多重分形谱Δα计算值Table 2 Calculated value of the multi-fractal spectrum Δα of the soil’s reconstruction spectrum under the Cu pollution gradient with different concentrations

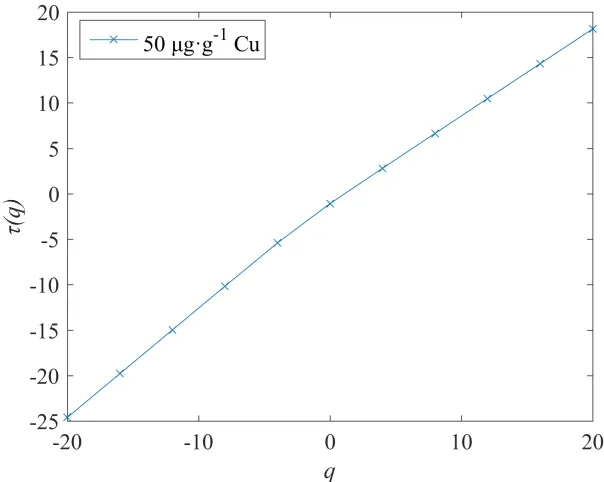
图6 50 μg∙g-1 Cu污染下土壤重构光谱τ(q)与q关系Fig. 6 Relationship of the soil’s reconstruction spectrum τ(q) and q under 50 μg∙g-1 Cu pollution gradient

式（6）和式（7），可得 50 μg∙g-1Cu 污染下土壤重构光谱多重分形谱参量Δα，同理可得，所对应的不同Cu污染梯度下土壤重构光谱多重分形谱宽度Δα的计算值，见表2。

由多重分形谱参量 Δα 可知，0～150 μg∙g-1Cu（土壤样品 Cu质量分数：20～120 μg∙g-1）污染下土壤光谱 Δα值随污染水平升高而降低，200～1200 μg∙g-1Cu（土壤样品 Cu 质量分数：160～740 μg∙g-1）污染下土壤光谱Δα值具有随污染水平升高而升高的趋势。据此推断，120～160 μg∙g-1（150～200 μg∙g-1Cu添加量）为土壤 Cu污染的界限浓度，与土壤Cu污染一阶导数距离分析结果一致。

由以上分析可知，土壤Cu污染光谱一阶导数距离和多重分形分析预测的土壤Cu污染的界限浓度为 120～160 μg∙g-1。

3.2 土壤Cu污染含量预测

根据不同处理水平Cu污染下土壤光谱一阶导数距离最大值及多重分形谱参量Δα值划分的土壤Cu 污染的界限浓度（120～160 μg∙g-1），建立土壤Cu污染的浓度预测模型。模型参数选择不同处理水平Cu污染下土壤光谱多重分形谱参量Δα、反射率一阶导数最大值、反射率最大值、含水率、有机质。0～150 μg∙g-1Cu污染梯度下土壤Cu含量预测模型参数为反射率、有机质及多重分形谱参量Δα值，预测模型选用多元线性回归模型（Multiple Linear Regression Analysis，MLR），模型 R2为 0.998，RMSE为 0.25（表 3）。200～1200 μg∙g-1Cu 污染梯度下土壤Cu含量预测模型参数为多重分形谱参量Δα值、反射率最大值、含水率、有机质、一阶导数最大值，预测模型选用 MLR，模型 R2为 0.992，RMSE为47.3（表 3）。

表3 多元线性回归模型（MLR）预测土壤Cu含量Table 3 Prediction of the soil’s Cu content using a multiple linear regression (MLR) model

4 讨论

本实验采样土壤来自于同一地区，并进行了粒径筛选及均匀混合，虽然不同样品的有机质含量与含水率有所差异，但不同样品Cu浓度的变异系数明显高于有机质含量与含水率的变异系数（表4）。因此，不同样品的差异性重点体现在所使用的化学试剂 CuSO4∙5H2O上，重金属Cu是以离子态存在的，所测得的土壤Cu污染光谱的差异主要体现在Cu离子的含量上（Maliki et al.，2014；Paresh et al.，2016）。为确保所测数据能尽量反映土壤本身的光谱特征，减少太阳光散射的影响，数据采集时间选择11:00—14:00之间，在5月晴朗无云、风力不超过5级的天气进行，SVC光谱仪镜头垂直于样品中心（李婷等，2012；黄芝，2017），获取的样品光谱数据范围为直径为8 cm的圆。根据实验设计可知，每份样品平行采集3次光谱，本研究所使用的数据为每份样品3组数据的平均值，因此从样品的选择、数据采集到数据应用3方面可知数据具有一定的可靠性和科学性。

表4 土壤Cu污染样品中Cu浓度、有机质含量及含水率统计分析Table 4 Analysis of Copper concentration, organic matter and water content in soil Copper contamination samples

前人对土壤重金属污染光谱的研究基本是利用整体波段区间内（Maliki et al.，2014；Paresh et al.，2016；Gholizadeh et al.，2015）或局部波段区间内（Stazi et al.，2014；Chen et al.，2016）反射率的导数变换，且根据前人经验可知，570～830 nm波段范围内土壤光谱反射率与土壤中有机质含量具有较强的相关性，土壤有机质含量与土壤重金属浓度也具有较强的相关性（宋练等，2014；Paresh et al.，2016）。因此，本研究选用了538～834 nm波段区间（Liu et al.，2011；Lu et al.，2007）的不同处理水平土壤Cu污染的光谱数据进行土壤Cu污染检测，一阶导数虽然能够放大光谱的细节差异（Wu et al.，2005；Fard et al.，2016），但是对于无光谱特征的土壤光谱数据的特征波段提取效果并不明显，因此引入了一阶导数距离。以未受污染的土壤光谱为基准曲线，对不同处理水平土壤Cu污染光谱数据与未受污染的土壤光谱数据进行运算，然后对不同处理水平土壤Cu污染光谱的一阶导数距离（差值）进行对比分析，以增大土壤Cu污染光谱之间的差异（Rathod et al.，2015；Maliki et al.，2012），并结合一阶导数距离最大值所在波段的不同，探索土壤Cu污染的界限浓度及光谱特征波段。对局部波段区间内不同处理水平Cu污染土壤光谱进行一阶导数距离分析后，再对整体光谱进行EMD去噪（贺利芳等，2017；王金贵等，2017；黄翔，2017）及多重分形微弱特征分析（姚精明等，2016；王晓乔等，2016；李楠等，2017），根据多重分形谱参量Δα随重金属浓度变化而变化的趋势，同样得到土壤Cu污染的界限浓度。与前人研究不同的是，本研究从整体到局部对土壤Cu污染光谱的分析得到的界限浓度一致，结果的准确性较高，实现了土壤Cu污染界限浓度的划分。

基于土壤有机质含量与土壤光谱和重金属浓度之间的相关性，本研究所选用的土壤Cu浓度预测模型参数为集中在570～830 nm波段范围内的土壤光谱反射率，再结合整体光谱多重分形谱参数可以探索不同浓度Cu污染的光谱细节差异的能力，进行了土壤Cu浓度的预测，可以提高预测模型的精度。查阅相关文献可知（Rathod et al.，2015；Xie et al.，2012；Wu et al.，2015；Maliki et al.，2014；Stazi et al.，2014），土壤Cu浓度最佳预测模型R2为 0.92，As、Pb、Ar浓度最佳预测模型的 R2为 0.96，但模型的 RMSE相对较大（表 5），因此，本研究预测模型的R2及RMSE均得到了较好的效果。

5 结论

多重分形谱参量Δα值和一阶导数距离最大值可作为土壤Cu污染界限浓度划分和光谱特征波段提取的依据，结合土壤Cu污染光谱反射率、土壤中有机质含量及土壤含水率构建的MLR模型可有效预测土壤Cu浓度，主要结论如下：

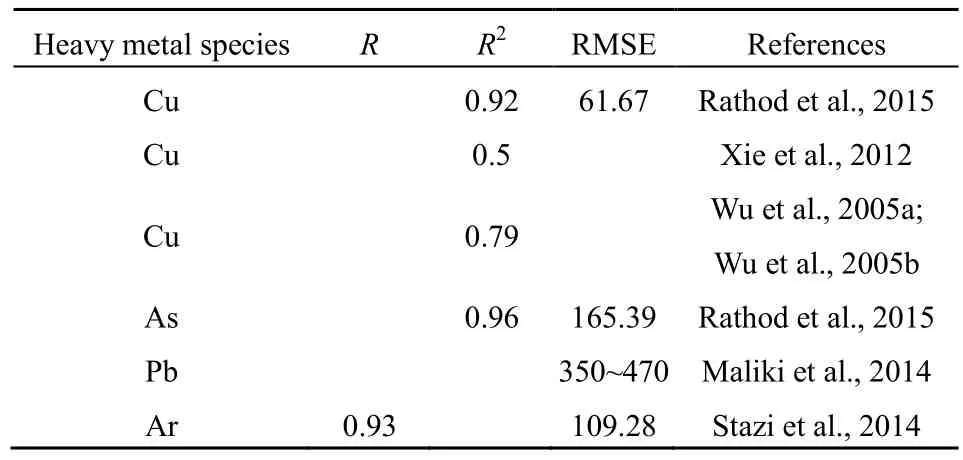
表5 土壤重金属含量预测模型精度对比Table 5 Comparison of the precision of the model for predicting the heavy metal content in the soil

（1）土壤Cu 污染的界限浓度为 120～160 μg∙g-1；土壤 Cu污染的特征波段区间为 730～760 nm 和540～590 nm。

（2）以 120～160 μg∙g-1为界限浓度，当土壤 Cu浓度在 20～120 μg∙g-1和 160～740 μg∙g-1时，分别建立MLR模型预测土壤中Cu浓度，该模型精度较高（R2＞0.99），RMSE 较小（RMSE＜50）。